K-近邻算法实战
前言:在彻底摸透《机器学习实战》课程中海伦约会网站配对案例之后,本次博客我将通过对案例的理解,运用k-近邻算法自己写一个关于鉴别一个学生是否是集美大学学生的程序
目录
一、算法样本数据集
二、k-近邻算法实现
三、读取数据集方法
四、图形可视化数据
五、数据归一化处理
六、测试算法准确率
七、算法实现
实验总结
一、算法样本数据集
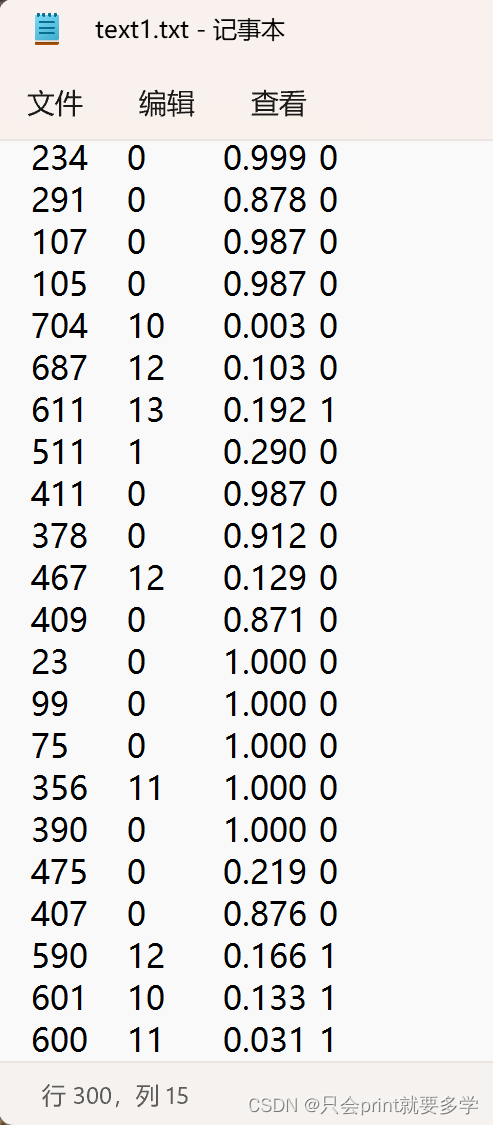
根据本届同专业同学的高考成绩(受地区教育资源原因,大概成绩区间在540-620之间)、近15天内刷卡进入图书馆次数、玩游戏所占日常个人时间比值。这三个特征值作为判断标准来作样本集合,将样本数据存储在自己编撰的text1.txt文本文件中,样本数量总共有300个,截图如下:
二、k-近邻算法实现
k-近邻算法的实现与之前写的博客中对k-近邻算法实现的理解相同,代码块部分并未作修改。
参考博客连接:
只会printf就要多学的k-近邻算法海伦网站配对案例分析
def knn(inX,dataSet,labels,k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort()
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]三、读取数据集方法
读取数据集的方法也和之前博客对读取数据集的分析差不多,但是由于样本数据都是自己手打的,所以中间可能有些'\t'后又多按了空格什么的,在初次读取文本文件时,读取出来的有些数据格式不统一,在打开文本查阅后又没发现不妥之处,于是在中间加了一句line = line.replace(' ','\t'),将空格全部替换成'\t',这样在后面去掉'\t'之后数据格式全部统一了
def readFile(filename):
fr = open(filename)
lines = fr.readlines()
line_num = len(lines)
character_Mat = zeros((line_num,3))
label_Mat = []
index =0
for line in lines:
line = line.strip('\n')
line = line.replace(' ','\t')
line_list = line.split('\t')
character_Mat[index,:] = line_list[0:3]
label_Mat.append(int(line_list[-1]))
index = index+1
return character_Mat,label_Mat
四、图形可视化数据
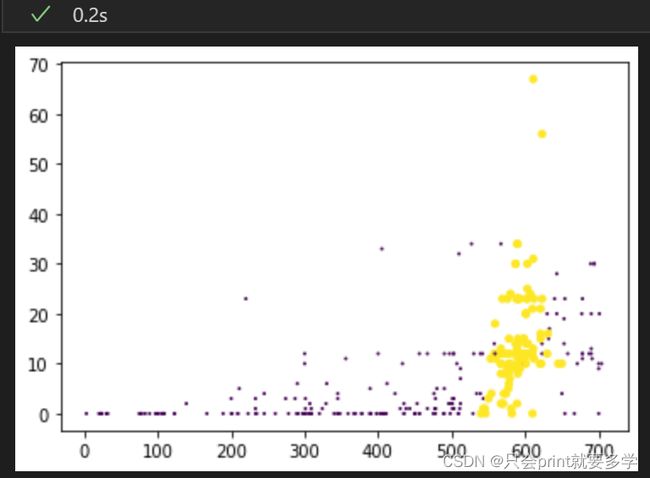
用图形化来观察数据样本分布是非常直观的一种选择,二维图像如下所示:(选取高考成绩和近15天进入图书馆次数为x轴和y轴)
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x=character_Mat[:,0]
y=character_Mat[:,1]
z=character_Mat[:,2]
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(x,y,15.0*array(label_Mat)+1,15.0*array(label_Mat)+1)
plt.show()
改进:在考虑样本特征有三项之后,思考能否用三维图像看看数据分布,于是自行查找了matplotlib中三维图像的代码,并加以改写,得到结果如下
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x=character_Mat[:,0]
y=character_Mat[:,1]
z=character_Mat[:,2]
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x,y,z,c=15.0*array(label_Mat)+1,s=15.0*array(label_Mat)+1)
plt.show()但是从图像上来看二者的差异并不是很明显,或许是因为我自己的数据样本的问题
五、数据归一化处理
归一化处理同上一篇博客分析,目的是使得不让某些特征对分类判断的占比过大,于是将每一项特征值都处理成0-1的区间
def autoNorm(dataSet):
min = dataSet.min(0)
max = dataSet.max(0)
ranges = max - min
normDataSet = zeros(shape(dataSet))
num = dataSet.shape[0]
normDataSet = dataSet - tile(min, (num,1))
normDataSet = normDataSet / tile(ranges, (num,1))
return normDataSet,ranges,min
六、测试算法准确率
在分类测试样本集和训练样本集中,需要人为的界定一些规则,使得测试样本和训练样本有所区别,而不是简单的前30%做测试和后70%做训练,但是在本次实验中,所有样本数据的排列本身就是随机的,所以可以随意分类测试样本和训练样本
def datingClassTest():
hoRatio = 0.20
character_Mat, label_Mat = readFile('D:/text1.txt')
normMat, ranges, min = autoNorm(character_Mat)
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = knn(normMat[i, :], normMat[numTestVecs:m, :], label_Mat[numTestVecs:m], 3)
print("训练预测结果: %d, 真实值: %d" % (classifierResult, label_Mat[i]))
if (classifierResult != label_Mat[i]): errorCount += 1.0
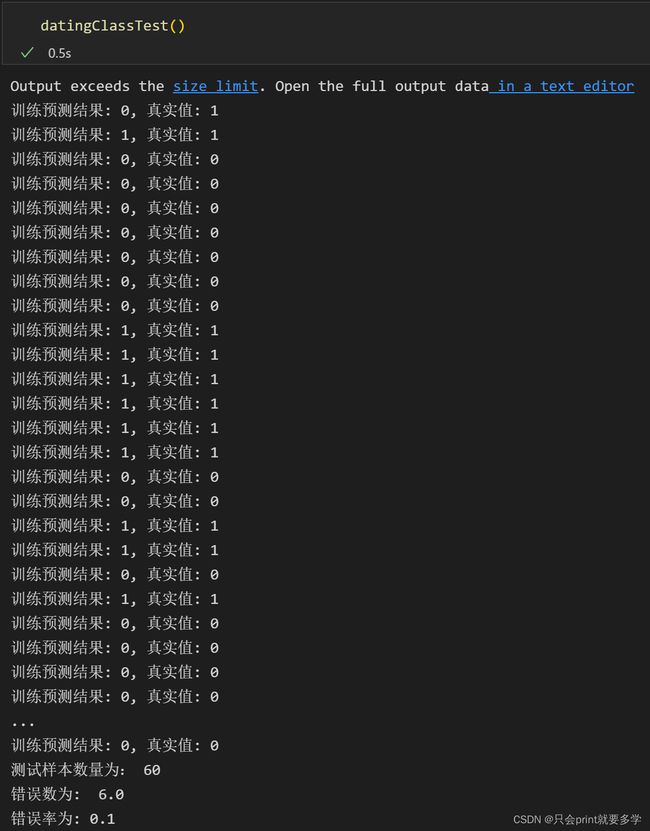
print("测试样本数量为:",numTestVecs,"\n错误数为: ",errorCount,
"\n错误率为:" ,(errorCount / float(numTestVecs)))
在k=3的算法中:60个测试样本中,有6个与预测值有误,错误率为0.1
当把k取10时:60个测试样本中,有8个与预测值有误,错误率为0.133333
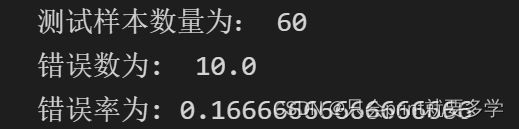
k取15时:60个样本中,有10个与预测值有误,错误率为0.1666666
把k取20时:60个样本中,有9个与预测值有误,错误率为0.15
在多次修改k值并查看测试样本后发现,当k值在(1,6)时,错误率都是0.1,当k值往后继续增大时,错误率始终比0.1大,所以对于我这个数据样本,k值在(1,6)区间是最合适的,k的取值与数据样本间是有很大关联
七、算法实现
def classifyPerson():
resultList = ["很大可能是","很大可能不是"]
score = float(input("请输入高考分数"))
library_count = float(input("请输入近15天内进入图书馆次数"))
game_rate = float(input("游戏时常占比"))
character_Mat,label_Mat = readFile('D:/text1.txt')
normMat, ranges, minVals = autoNorm(character_Mat)
inArr = np.array([score, library_count, game_rate ])
#先把输入的样本值归一化,再与已经归一化的数据样本比较
classifierResult = knn((inArr-minVals)/ranges, normMat, label_Mat, 3)
print("高考成绩 ",score,"\n近15天内进入图书馆次数 ",library_count, "\n游戏时常占比: " ,game_rate, "\n预测结果为: " ,resultList[classifierResult - 1],"集美大学的学生")
看看输入几个新样本,结果如何
实验总结:
对于k-近邻算法,k的取值跟样本数据的分布分布情况关联很大,需要多次取不同的k值进行比较,根据错误率来选取合适的k值。