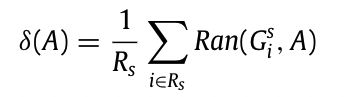Influence maximization based on the realistic independent cascade model
基于现实的独立级联模型的影响最大化
- 前言
-
- 文章内容
-
- 摘要
- 背景
- 真实独立级联模型
- R-greedy算法介绍
-
- step1:
-
- 计算 δ ( C ) \delta(C) δ(C)
- 确定最大的 δ ( C ) \delta(C) δ(C)
- step2:
- step3:
- M-greedy算法
-
- step1:
- step2:
- step3:
- D-greedy算法
- 实验
-
- 数据集
- 对比算法
- 实验结果
-
- 不同的概率分布
- 算法的时间复杂度
- 结论
前言
2020年发表在KBS上的一篇,是影响力最大化方面对影响力传播进行改进的文章。文章的highlights:提出了适合现实世界网络的现实独立级联(RIC)模型;在RIC模型的基础上,提出了三种新的播种算法;M-greedy和D-greedy减少了R-greedy的时间消耗;在不同网络上的实验证明了所提算法的优越性。

https://www.sciencedirect.com/science/article/pii/S0950705119305702
文章内容
摘要
In order to propagate information through the social network, how to find a seed set that can affect the maximum number of users is named as influence maximization problem. A lot of works have been done on this problem, mainly including two aspects: establishing a reasonable information diffusionmodel and putting forward the appropriate seeding strategy. However, there are few models in the existing ones that consider the acceptance probability of candidate seed nodes in social networks. So in this paper, we consider and solve this problem by introducing a more realistic model, which is the proposed Realistic Independent Cascade (RIC) model. Based on the RIC model, many state-of-the-art seeding algorithms perform not so well because there is no mechanism on dealing with the acceptance probability. So based on the RIC model, we propose a new seeding strategy which is called R-greedy.Furthermore, M-greedy algorithm is proposed to reduce the time complexity of R-greedy. Then, D-greedy algorithm which not only increased the performance but also reduced the time complexity ofR-greedy is proposed by combining the advantages of R-greedy and M-greedy. Experiments on thereal-world networks and synthetic networks demonstrate that the proposed R-greedy, M-greedy andD-greedy algorithms outperforms state-of-the-art algorithms.
为了在社会网络中传播信息,如何找到一个能够影响最大数量用户的种子集,被称为影响力最大化问题。在这个问题上已经做了很多工作,主要包括两个方面:建立一个合理的信息扩散模型和提出适当的播种策略。然而,在现有的模型中,很少有考虑到社交网络中候选种子节点的接受概率。 在本文中,我们通过引入一个更现实的模型,即提出的现实独立级联(RIC)模型来考虑和解决这个问题。基于RIC模型,许多最先进的播种算法表现得不是很好,因为没有处理接受概率的机制。因此,基于RIC模型,我们提出了一种新的播种策略,即R-greedy。此外,我们还提出了M-greedy算法来降低R-greedy的时间复杂度。然后,结合R-greedy和M-greedy的优点,提出了D-greedy算法,该算法不仅提高了性能,还降低了R-greedy的时间复杂度。在真实世界网络和合成网络上的实验表明,所提出的R-greedy、M-greedy和D-greedy算法的性能超过了最先进的算法。
背景
常用的IC模型没有考虑到现实信息传播的一些特征。例如,在选种子节点时,选中的用户不一定愿意成为种子节点;或者在信息传播时,用户 u u u尝试传播信息给用户 v v v,用户 v v v是否会接受是未知的。考虑这两种情况,为每个用户设置一个概率值,称为接受概率(acceptance probability),反应用户接受信息的概率。
接受概率的意义:
- 在寻找种子节点的过程,某个节点根据特定准则被选中时,接受概率表示其称为种子的概率;
- 在信息传播的过程,传播概率表示其从邻居接受信息的概率。
并且每个用户的接受概率不同。
所以提出了RIC(Realistic Independent Cascade) 模型,不同节点具有不同的接受概率,并遵循一定的分布,两个节点之间的传播概率也不同,遵循一定分布。基于RIC模型,考虑如何选择种子节点,需要同时考虑影响和接受概率,假设两个用户,一个接受概率较小但是影响力大,一个接受概率大但是影响力小,如何选择?因此提出了R-greedy。又提出M-greedy减少R-greedy的时间消耗。最后又提出D-greedy进一步提高R-greedy的性能。
主要贡献:
- 提出了更适合真实世界网络的真实独立级联模型(RIC)。
- 基于RIC模型,提出了新的种子节点选择策略R-greedy。
- 基于R-greedy,提出启发式策略M-greedy,减少R-greedy的时间消耗。进一步结合两者提出更强的D-greedy。
- 在真实世界网络和合成网络上实验,证明提出的三种算法在RIC模型上优于其他算法。
真实独立级联模型
图中节点有两种状态:活跃和非活跃。在初始,所有节点都是非活跃的,节点可以通过1)被选为种子节点;2)被邻居激活,变为活跃态。
给每个节点一个接受概率, p v , p ∈ [ 0 , 1 ] p_v, p\in[0,1] pv,p∈[0,1],它是随机变量,遵循分布 f v f_v fv。因此节点 v v v愿意接受免费样本,这意味着成功激活,当它被选为种子并提供免费样本时,其接受概率为 p v p_v pv。此外,当信息从其邻居成功传播到节点 v v v时,节点 v v v以接受概率 p v p_v pv接受该信息。
对于边,有传播概率 p u , w p_{u,w} pu,w,表示活跃节点 u u u,以传播概率沿着边 < u , w >
但是难以精确每个节点每条边的概率,所以选择采用不同分布来模拟。
- RIC模型的传播过程:
影响传播过程以离散的时间步展开。
时间 t t t,节点 u u u被激活,它有一次机会去传播信息给它每一个非活跃的出度邻居节点 w w w,传播概率是 p u , w p_{u,w} pu,w。
如果 w w w有多个新的活跃邻居,它们的影响传播可以无序排列。
一旦信息从节点成功从 u u u传播到 w w w,并且节点 w w w愿意接受它(考虑概率吗??),我们认为节点 w w w成功被 u u u激活并变成活跃态,它将在时间 t + 1 t+1 t+1去影响它的非活跃出度邻居。
无论 u u u是否成功激活 w w w,它在接下来的步骤都不会影响任何节点。
知道没有新的激活节点,上述过程中止。
图1是信息传播过程的实例。图a,节点1作为种子节点没有被成功激活。图b,节点1作为种子节点被成功激活了,但是没有成功传播信息。图c,节点1作为种子节点被成功激活且信息也成功传播了但是节点2不愿接受信息。图d,节点1作为种子节点被成功激活且信息也成功传播了,节点2成功接受了信息,并且成功传播信息给节点3,但是节点3不愿接受信息。
RIC公式化:
G = ( V , E , f v , f e ) G=(V,E, f_v,f_e) G=(V,E,fv,fe), V V V表示节点集, E E E表示边集, f v f_v fv是接受概率 p v p_v pv的分布, f e f_e fe是传播概率 p u , w p_{u,w} pu,w的分布。用 n n n表示节点集 V V V的个数。种子节点预算个数 B B B,如果节点被选为种子但没有被激活则流失一个预算,所以最终种子节点的个数小于等于 B B B。
R-greedy算法介绍
R-greedy的思想是根据一定的准则从候选集中选择种子节点,同时考虑候选节点的影响和接受概率。
三个步骤:
- 根据节点影响选择候选种子节点集合 C C C
- 给出从候选种子集中选择种子集的准则,记为 T T T
- 从候选集合 C C C中选择种子集合 A A A
step1:
根据节点影响选择候选种子节点集合 C C C。这里不考虑接受概率,也就是被选为种子的节点一定会被激活。候选集 C C C在传播前就选定,个数为 k k k个, k k k要大于预算 B B B, k ∈ K k\in K k∈K。

K K K是 k k k的取值,是离散的,每两个取值之间相差十,最大的取值 k I k_I kI是节点的个数 n n n。
如果 k i − 1 < B ≤ k i ( i = 1 , 2 , ⋯ , I ) k_{i-1}
定义 δ ( C ) \delta(C) δ(C)为候选集C的影响传播,开始只有C中的节点被激活了,信息传播后,激活节点数量的期望就是 δ ( C ) \delta(C) δ(C)。最终的 δ ( C ) \delta(C) δ(C)满足 δ ( C ) ≥ δ ( C ′ ) \delta(C)\geq\delta(C') δ(C)≥δ(C′), C ′ C' C′表示其他个数为k的候选集合。
计算 δ ( C ) \delta(C) δ(C)
定义1:
一个现实图 G = ( V , E , f v , f e ) G=(V,E, f_v,f_e) G=(V,E,fv,fe),每条边有两种状态{live, not live},表示信息是否能成功传播,每个节点也有两个状态{active, not active},表示是否接受信息。
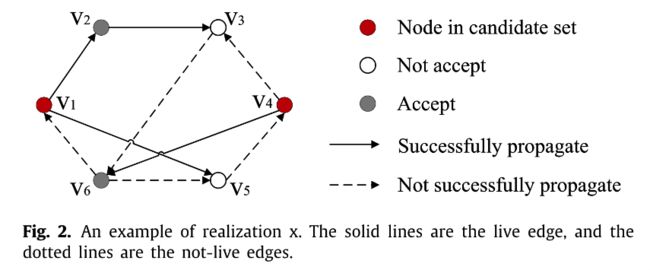
图2是传播中可能会出现的一种情况,还可能会出现很多其他的情况。
在种子集C的情况下,图2的扩散计作 δ x ( C ) \delta_x(C) δx(C)。
P r o b ( x ) Prob(x) Prob(x)就是出现x这张传播情况的概率, δ ( C ) \delta(C) δ(C)就是不同情况的加权平均。
传播情况有多少种?每种情况的权重是多少?不好计算。
这里其实就取一个相对较大的值 R m R_m Rm,重复 R m R_m Rm次扩散取平均。
δ ( C ) = ∑ r : 1 → R m δ r ( C ) R m \delta(C)=\frac{\sum_{r:1\rightarrow R_m}\delta_{r}(C)}{R_m} δ(C)=Rm∑r:1→Rmδr(C)
确定最大的 δ ( C ) \delta(C) δ(C)
贪心算法,边缘效益一步步确定候选集
选取边际收益最大的节点
w i w_i wi表示第i个候选节点
算法分析:
- 输入: G = ( V , E , f v , f e ) G=(V,E, f_v,f_e) G=(V,E,fv,fe)和候选集大小 k k k
- line1: 初始化候选集列表 C C C
- line2-4: 将每个节点的边际收益设为正无穷
- line5: 在候选集个数小于 k k k时进行循环,以下每循环一次添加一个候选节点
- line6-8: 对于不在候选集中的节点, h v h_v hv标签设为false,表示边际收益没有更新
- line9: 循环
- line10: 选出边际收益最大的节点 v ∗ v^* v∗
- line11-13: 如果 v ∗ v^* v∗的 h v h_v hv标签是 t r u e true true表示边际收益更新了,该节点加入候选集返回line5
- line14-17: 否则,计算 v ∗ v^* v∗的边际收益,并更新 h v h_v hv标签为true
- line18: 输出 C C C
step2:
给出从候选种子集中选择种子集的准则,记为 T T T
这一步就要考虑候选节点的接受概率。

w i w_i wi是第i个候选节点
H w i H_{w_i} Hwi边际收益
p w i p_{w_i} pwi接受概率
step3:
从候选集合 C C C中选择种子集合 A A A
一步步选择节点。给定预算B,首先选择T值最高的,尝试选为种子节点,如果接受,则成功选为种子节点,不接受则下一步继续尝试,直到成功选为种子节点;然后选择T值第二高的,尝试直到成功选为种子节点。每次尝试用一次预算B。

M-greedy算法
提升R-greedy的效率,也就是加速蒙特卡洛模拟。采取方法是去掉一些节点,减少遍历节点数。
根据Section 6,节点的影响扩散存在显著差异,较少的节点有大影响力,大部分节点只有较小的影响力,这也是现实网络的特点。
M-greedy的思想:计算平均影响范围,将低于平均的节点删掉。
step1:
用蒙特卡洛模拟计算每个节点的影响 δ ( v ) \delta(v) δ(v),并计算影响平均值 1 n ∑ v ∈ V δ ( v ) \frac{1}{n}\sum_{v\in V}\delta(v) n1∑v∈Vδ(v)。
step2:
将满足 δ ( v ) < 1 n ∑ v ∈ V δ ( v ) \delta(v)<\frac{1}{n}\sum_{v\in V}\delta(v) δ(v)<n1∑v∈Vδ(v)的节点删除
step3:
跑R-greedy得到种子集。
D-greedy算法
在R-greedy和M-greedy算法中,用蒙特卡洛模拟来计算影响扩散 δ ( ⋅ ) \delta(\cdot) δ(⋅),现在用一种思维快照来估计静态贪婪。
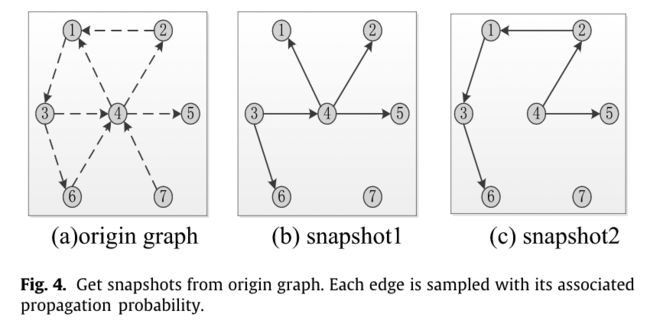
快照 G s G^s Gs是从社交网络 G G G中采样来的。 G G G中的每条边 ⟨ u , w ⟩ ⟨u,w⟩ ⟨u,w⟩用其相关的传播概率 p u , w p_{u,w} pu,w进行采样,以获得快照 G i s G^s_i Gis
在图4中,快照1和2就是通过对边采样得到的。
在每个快照 G i s G_i^s Gis计算,计算A种子集合的影响扩散,然后取所有平均作为 δ ( A ) \delta(A) δ(A)。给定网络G,生成 R s R_s Rs个快照。
通过删减的方式获取快照
R s R_s Rs是快照数量, R a n ( G i s , A ) Ran(G_i^s,A) Ran(Gis,A)是快照上由种子集A激活的节点数。
那么在RIC模型上,利用网络,子图和预算选择种子节点。

 算法分析:
算法分析:
- 输入:网络,子图,预算
- line1: 初始化种子节点集A
- line2: 在预算B用完之前循环
- line3: 对不在A集中的节点,边际收益设为0,
- line4-8: 对每个快照,计算每个非种子节点的边际收益
- line9: 取接受概率与边际收益相乘最大的节点
- line10-18: 尝试激活该节点,每尝试一次用掉一次预算。
实验
数据集
- Wiki-vote network,7115个节点,103689条有向边。
- CA-HepTh network,9877个节点,51971条有向边。
- Ca-Condmat network,23133个节点,93497条无向边。
- LFR networks

n n n节点数
< k >
k m a x k_{max} kmax最大度
β \beta β社区节点数的幂律分布指数
γ \gamma γ度的幂律分布指数
μ \mu μ混合参数,是节点与外部社会的节点连接的概率
接受概率和传播概率的分布:
高斯分布 期望值 μ \mu μ,偏差 σ 2 \sigma^2 σ2
幂律分布 y = c ⋅ x t y=c\cdot x^t y=c⋅xt
指数分布 λ \lambda λ
均匀分布
对比算法
1.R-greedy:对于每个 δ ( ⋅ ) \delta(\cdot) δ(⋅),一万次蒙特卡洛
2.M-greedy:同上
3.D-greedy:去 R s = 100 R_s=100 Rs=100,也就是100个快照
4.CELF-greedy:给定种子集合A的预算,它在信息扩散过程之前被选择,当扩散开始时,由于种子的接受概率,并不是所有的种子都能被成功激活,因此影响A的扩散(即激活的种子的数量)是由成功激活的种子引起的。对于扩散函数 δ ( ⋅ ) \delta(\cdot) δ(⋅)的每个值,进行了10000次蒙特卡罗模拟以获得准确的估计。
5.Static Greedy:如第6节所述,我们从给定的社会网络G中抽取了100个快照,然后在扩散过程中,在这100个快照上选择种子集。但由于网络中的节点都有接受概率,种子并不能保证被激活而产生影响扩散,也就是说,只有能成功激活的种子才会产生影响扩散。CELF技术被应用于以下实验中
6.BKRIS:需要 θ \theta θ反向可达集。 θ = 2 n ( ( 1 − 1 / e ) ⋅ α + β ) 2 O P T ⋅ ε 2 \theta=\frac{2n((1-1/e)\cdot\alpha+\beta)^2}{OPT\cdot\varepsilon^2} θ=OPT⋅ε22n((1−1/e)⋅α+β)2
O P T OPT OPT影响力最优种子集
ε \varepsilon ε蒙特卡洛模拟的误差
α = l log n + log 2 \alpha=\sqrt{l\log n+\log 2} α=llogn+log2
β = ( 1 − 1 / e ) ⋅ ( log k n + l log n + log 2 ) \beta=\sqrt{(1-1/e)\cdot(\log_k^n+l\log n+\log 2)} β=(1−1/e)⋅(logkn+llogn+log2)
n n n是节点数
l = 1 , ε = 0.2 l=1,\varepsilon=0.2 l=1,ε=0.2
给定θ个反向可达集,可以得到种子集,由于种子的接受概率,不是所有的种子都能成功激活,所以A的影响传播是由成功激活的种子引起的。
实验结果
不同的概率分布
 在CA_HepTh上,四种不同的概率分布。x轴是节点的影响 δ ( v ) \delta(v) δ(v),y轴是统计数量。我们可以看到,节点的影响力分布存在显著差异,更少的节点具有更大的影响力,而大多数节点的影响力较小,这主要小于所有节点的影响力平均值。
在CA_HepTh上,四种不同的概率分布。x轴是节点的影响 δ ( v ) \delta(v) δ(v),y轴是统计数量。我们可以看到,节点的影响力分布存在显著差异,更少的节点具有更大的影响力,而大多数节点的影响力较小,这主要小于所有节点的影响力平均值。
- (a) < δ ( v ) > = 3.662 <\delta(v)>=3.662 <δ(v)>=3.662,77.99%的节点小于该值
- (b) < δ ( v ) > = 1.4327 <\delta(v)>=1.4327 <δ(v)>=1.4327,73.85%的节点小于该值
- (c) < δ ( v ) > = 3.8168 <\delta(v)>=3.8168 <δ(v)>=3.8168,78.58%的节点小于该值
- (d) < δ ( v ) > = 2.7926 <\delta(v)>=2.7926 <δ(v)>=2.7926,78.86%的节点小于该值
图6-11展示了随着节点的减少,M-greedy的性能接近R-greedy。

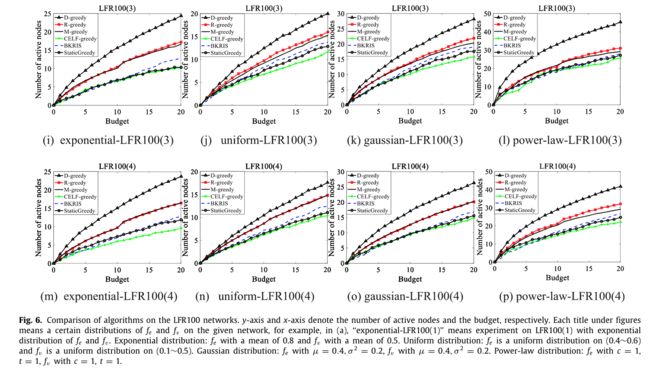
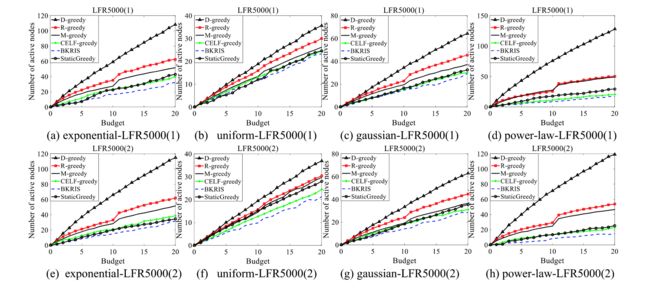
图6,在LFR100(1), LFR100(2), LFR100(3) and LFR100(4)四个网络上分别设置不同的概率分布。
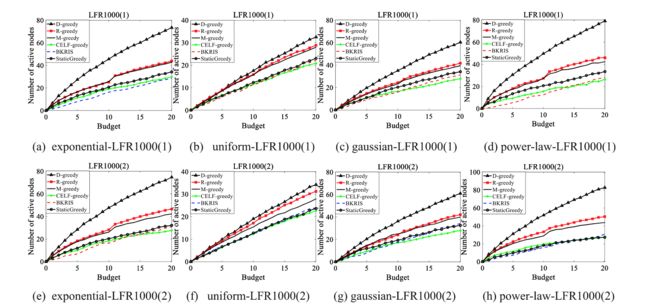
图7,在LFR1000(1), LFR1000(2), LFR1000(3) and LFR1000(4)四个网络上分别设置不同的概率分布。

图8,在LFR1000(1), LFR1000(2), LFR1000(3) and LFR1000(4)四个网络上分别设置不同的概率分布。
总而言之,对于所有12个LFR网络,我们为它们设置了不同的分布,D-greedy的性能在所有情况下都优于其他网络,而M-greedy的表现,在减少网络节点的情况下,比R-greedy更接近或更差。

图9,在CA-HepTh网络上,不同概率分布都是D-greedy表现最好,在(d)图中,R-greedy比M-greedy好。

在图10中,Wiki-Vote网络上,D-greedy也是最好的。
在图11中,ca-Condmat网络上,D-greedy也是最好的。
算法的时间复杂度
表4 运行时间
结论
提出了RIC模型来捕捉扩散过程中的不确定性。在RIC模型中,当一个节点被选为种子或者当信息被传播到一个节点时,该节点不能保证接受它,因此设置了一个遵循一定分布的随机值;除此之外,两个节点之间的传播概率不是相同的值,它遵循一定的分布,反映了同一信息在不同个体之间的传播是不同的。基于RIC模型,我们提出了R贪婪算法,该算法根据一定的准则从候选集中选择种子集,并提出了M贪婪算法,大大减少了R贪婪的时间消耗。最后,结合R-贪婪和M-贪婪的优点,提出了D-贪婪算法,与R-贪婪算法和M-贪心算法相比,D-贪婪方法的性能更好,且耗时更少。