机器学习(周志华)学习笔记六:贝叶斯分类器(上)
一、贝叶斯分类器
贝叶斯分类器包括朴素贝叶斯分类器、半朴素贝叶斯分类器、贝叶斯网,本文主要介绍前两者。
三种分类器依照对属性间依赖关系的重视程度进行区分.朴素贝叶斯分类器假设属性间相互独立,互不影响。半朴素贝叶斯分类器假设属性间“独依赖”,即假设每个属性在类别之外最多仅依赖于其他一个属性。而贝叶斯网则更加突出了结点间的相互关系,贝叶斯网中变量可存在“同父结构”、“V型结构”、“顺序结构”三种典型的依赖关系。
二、贝叶斯分类器的基本思想
利用贝叶斯分类器进行决策,实质上就是判断使后验概率P(c|x)最大的类别c,即在已知数据x的情况下,最有可能发生的类别c,就是决策划分的类别。公式如下:

按照上述想法,可以依照贝叶斯公式将后验概率转化为显眼概率,公式如下:
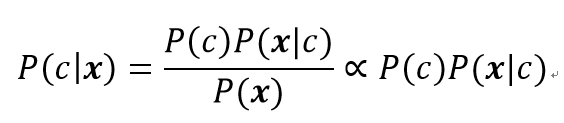
三、朴素贝叶斯分类
设向量x由d个属性组成,xi为向量x在第i个属性上的取值。朴素贝叶斯分类假设每个属性的取值相互独立。公式如下:
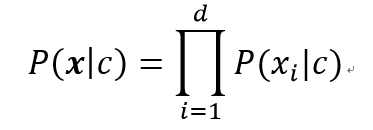
四、半朴素贝叶斯分类
假设向量x中属性xi“独依赖”,公式如下:

值得说明的是,式中m’可以限制“独依赖”属性依赖性的强弱,对于依赖性较弱的“独依赖”属性进行舍弃,从而简化运算。
五、关于概率求解问题的说明
对于离散属性,概率求解十分简单,只需要进行计数,然后除以总数即可近似获得概率值。
对于连续属性,概率求解需要引入概率密度函数进行计算,通常使用高斯函数进行模拟。对于连续属性来说,在任意一个点取值的概率均为0,因此用该点的概率密度值代表该点发生概率的大小。
然而,在进行贝叶斯分类求解时,往往也会陷入高阶联合概率求解的问题。例如,对于概率P(xj | c, xi)进行求解,就需要依据xi,xj的连续性质,讨论四种可能情况。其中,当xi,xj均为连续变量时,会涉及到2个变量的联合概率密度,增加了计算量,而且当条件变量增多时,这个问题会更加突出。(注:关于四种情况的详细讨论,第七部分在代码中体现)
六、朴素贝叶斯分类部分代码
def calculate_likelihood(self, is_continuous, i, xi):
"""
计算i属性值xi的 P(xi|c)
"""
good_list = data.attrs_list[i][0:data.good_count]
bad_list = data.attrs_list[i][data.good_count:data.sample_count]
if is_continuous:
# 连续情况
m_good, v_good = self.calculate_parameters(good_list)
m_bad, v_bad = self.calculate_parameters(bad_list)
p_good = self.calculate_gauss(xi, m_good, v_good)
p_bad = self.calculate_gauss(xi, m_bad, v_bad)
else:
# 离散情况, 拉普拉斯修正
p_good = (self.calculate_count(xi, good_list) + 1) / (data.good_count + data.Ni_list[i])
p_bad = (self.calculate_count(xi, bad_list) + 1) / (data.bad_count + data.Ni_list[i])
return p_good, p_bad
def judge(self):
"""
计算概率,并进行判决
:return:分析结果、好瓜概率、坏瓜概率
"""
p_good, p_bad = self.calculate_pc()
print("pc", "good", p_good, "bad", p_bad)
for i in range(data.attrs_count):
if i < data.discrete_count:
is_continuous = False
else:
is_continuous = True
px_good, px_bad = self.calculate_likelihood(is_continuous, i, data.test_sample[i])
print(data.attrs_name[i], "good:", px_good, "bad:", px_bad)
p_good *= px_good
p_bad *= px_bad
if p_good > p_bad:
return "好瓜", p_good, p_bad
else:
return "坏瓜", p_good, p_bad
七、半朴素贝叶斯分类部分代码
def calculate_likelihood_i(self, is_continuous, i, xi):
"""
计算i属性值xi的概率P(c,xi)
:param is_continuous: xi是否为连续值
:param i: 属性标号
:param xi: xi的值
:return: p_good and p_bad
"""
if is_continuous:
# 连续情况:P(c,xi)=P(c)*P(xi|c)
pc_good, pc_bad = self.calculate_pc()
p_good, p_bad = self.calculate_likelihood(is_continuous, i, xi)
p_good *= pc_good
p_bad *= pc_bad
else:
# 离散情况
good_count = self.calculate_count_i(i, xi, 1)
bad_count = self.calculate_count_i(i, xi, 0)
p_good = (good_count + 1) / (data.sample_count + data.N * data.Ni_list[i])
p_bad = (bad_count + 1) / (data.sample_count + data.N * data.Ni_list[i])
return p_good, p_bad
def calculate_likelihood_ij(self, is_xi_continuous, is_xj_continuous, i, j, xi, xj):
"""
计算j属性值xj的条件概率P(xj|c,xi), 四种情况:xi、xj的连续性决定
:param is_xi_continuous:
:param is_xj_continuous:
:param i:
:param j:
:param xi:
:param xj:
:return: p_good and p_bad
"""
p_good = 0
p_bad = 0
if is_xi_continuous and is_xj_continuous:
# xi,xj 均连续,则利用二维高斯分布求解
good_list_i = data.attrs_list[i][0:data.good_count]
bad_list_i = data.attrs_list[i][data.good_count:data.sample_count]
good_list_j = data.attrs_list[j][0:data.good_count]
bad_list_j = data.attrs_list[j][data.good_count:data.sample_count]
r_good, mx_good, my_good, vx_good, vy_good = self.calculate_related_parameters(good_list_i, good_list_j)
r_bad, mx_bad, my_bad, vx_bad, vy_bad = self.calculate_related_parameters(bad_list_i, bad_list_j)
p_good = self.calculate_gauss2(r_good, mx_good, my_good, vx_good, vy_good, xi, xj)
p_bad = self.calculate_gauss2(r_bad, mx_bad, my_bad, vx_bad, vy_bad, xi, xj)
elif is_xi_continuous and not is_xj_continuous:
# 若xj离散,则P(xj| c, xi) = P(c, xi, xj) / P(c, xi) = P(xi| c, xj) * P(c, xj) / P(c, xi)
# 若所有数据相同,可能出现方差为 0 的情况,应加入极小值修正
p_good_xi, p_bad_xi = self.calculate_likelihood_i(is_xi_continuous, i, xi)
p_good_xj, p_bad_xj = self.calculate_likelihood_i(is_xj_continuous, j, xj)
good_index_list = self.get_list_i(1, j, xj)
bad_index_list = self.get_list_i(0, j, xj)
good_list = []
bad_list = []
for index in good_index_list:
good_list.append(data.attrs_list[i][index])
for index in bad_index_list:
bad_list.append(data.attrs_list[i][index])
m_good, v_good = self.calculate_parameters(good_list)
m_bad, v_bad = self.calculate_parameters(bad_list)
p_good = self.calculate_gauss(xi, m_good, v_good) * p_good_xj / p_good_xi
p_bad = self.calculate_gauss(xi, m_bad, v_bad) * p_bad_xj / p_bad_xi
elif not is_xi_continuous and is_xj_continuous:
# 若xi离散,则P(xj|c,xi)利用高斯求解
# 对方差加入极小值进行修正
good_index_list = self.get_list_i(1, i, xi)
bad_index_list = self.get_list_i(0, i, xi)
good_list = []
bad_list = []
for index in good_index_list:
good_list.append(data.attrs_list[j][index])
for index in bad_index_list:
bad_list.append(data.attrs_list[j][index])
m_good, v_good = self.calculate_parameters(good_list)
m_bad, v_bad = self.calculate_parameters(bad_list)
p_good = self.calculate_gauss(xj, m_good, v_good)
p_bad = self.calculate_gauss(xj, m_bad, v_bad)
elif not is_xi_continuous and not is_xj_continuous:
# xi, xj 均离散:根据书中公式
good_count_ij = self.calculate_count_ij(i, j, xi, xj, 1)
bad_count_ij = self.calculate_count_ij(i, j, xi, xj, 0)
good_count_i = self.calculate_count_i(i, xi, 1)
bad_count_i = self.calculate_count_i(i, xi, 0)
p_good = (good_count_ij + 1) / (good_count_i + data.Ni_list[j])
p_bad = (bad_count_ij + 1) / (bad_count_i + data.Ni_list[j])
return p_good, p_bad
def judge(self):
p_good = 0
p_bad = 0
for i in range(data.attrs_count):
xi = data.test_sample[i]
is_xi_continuous = data.continuous_list[i]
if self.calculate_count(xi, data.attrs_list[i]) > self.m:
pi_good, pi_bad = self.calculate_likelihood_i(is_xi_continuous, i, xi)
for j in range(data.attrs_count):
xj = data.test_sample[j]
is_xj_continuous = data.continuous_list[j]
pij_good, pij_bad = self.calculate_likelihood_ij(is_xi_continuous, is_xj_continuous, i, j, xi, xj)
pi_good *= pij_good
pi_bad *= pij_bad
p_good += pi_good
p_bad += pi_bad
if p_good > p_bad:
print('好瓜', 'p_good:', p_good, 'p_bad:', p_bad)
else:
print('坏瓜', 'p_good:', p_good, 'p_bad:', p_bad)
八、完整程序源码
【贝叶斯分类器.zip】