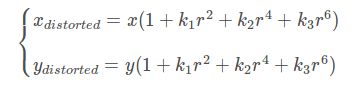知识归纳：相机标定

相机标定（持续更新中）

1、引言

​ 在图像测量过程以及机器视觉应用中，为确定空间物体表面某点的三维几何位置与其在图像中对应点之间的相互关系，必须建立相机成像的几何模型，这些几何模型参数就是相机参数。在大多数条件下这些参数（内参、外参、畸变参数）必须通过实验与计算才能得到，这个求解参数的过程就称之为相机标定（或摄像机标定）。无论是在图像测量或者机器视觉应用中，相机参数的标定都是非常关键的环节，其标定结果的精度及算法的稳定性直接影响相机工作产生结果的准确性。因此，做好相机标定是做好后续工作的前提，提高标定精度是科研工作的重点所在。

​ 标定的目的主要为解决两个问题：

​ a、确定世界坐标系下三维空间点与像素平面像素点间的转换关系（内外参）；

​ b、确定相机成像过程中的畸变系，用于图像矫正。

2、相机坐标系

其中，相机标定主要涉及到四大坐标系，分别为：

2.1、像素坐标系

为了描述物体成像后的像点在数字图像上（像平面）的坐标而引入，是我们真正从相机内读取到的信息所在的坐标系，单位为像素数目（pixel)。坐标系的原点在图像的左上角$O_0$，其中相机的理想主点（相机光轴与像平面的交点）为像平面的中心位置$O_1$（$u_0$,$v_0$)

2.2、图像坐标系

为了描述成像过程中物体从相机坐标系到图像坐标系的投影透射关系而引入，方便进一步得到像素坐标系下的坐标，单位为米(m)。坐标系的原点为相机主点$O_1$

2.3、相机坐标系

在相机建立的坐标系，为了从相机的角度描述物体位置而定义，作为沟通世界坐标系和图像/像素坐标系的中间一环。单位为米(m)。坐标系的原点为$O$，Z轴方向为相机光轴方向。

2.4、世界坐标系

用户定义的三维世界的坐标系，为了描述目标物在真实世界里的位置而被引入，单位为米(m)。

2.5、坐标系转换

相机标定的内容主要基于这四个坐标系，他们之间的转换关系如图所示，其中f为相机焦距，a为x方向上一个像素占多少长度单位的倒数，b为y方向上一个像素占多少单位长度的倒数，r为畸变参数，$u_0$和$v_0$为图像中心位置（主点）的坐标，$R_{3\ast 3}$为旋转矩阵，$T_{3\ast 1}$为平移矩阵。

3、相机模型

相机将三维世界中的坐标点（单位：米）映射到二维图像平面（单位：像素）的过程能够用一个几何模型来描述。opencv主要分为小孔模型 (pinhole camera model)和鱼眼模型 (fisheye camera model)，kalibr库主要分为小孔相机模型、全向相机模型（omnidirectional camera model ）、双球模型（double sphere camera model）、拓展统一相机模型（extended unified camera model ）。

3.1、针孔相机模型

相机将三维世界中的坐标点（单位：米）映射到二维图像平面（单位：像素）的过程能够用一个几何模型来描述，其中最简单的称为针孔相机模型 (pinhole camera model)，其框架如下图所示:

3.2、鱼眼相机模型

由于鱼眼镜头会产生极大的形变，因此针孔模型无法为鱼眼镜头建模。鱼眼镜头一般是由十几个不同的透镜组合而成的，在成像的过程中，入射光线经过不同程度的折射，投影到尺寸有限的成像平面上，使得鱼眼镜头与普通镜头相比起来拥有了更大的视野范围。下图表示出了鱼眼相机的一般组成结构。最前面的两个镜头发生折射，使入射角减小，其余的镜头相当于一个成像镜头，这种多元件的构造结构使对鱼眼相机的折射关系的分析变得相当复杂。

研究表明鱼眼相机成像时遵循的模型可以近似为单位球面投影模型。可以将鱼眼相机的成像过程分解成两步：

1.三维空间点线性地投影到一个球面上，它是一个虚拟的单位球面，它的球心与相机坐标系的原点重合。
2.单位球面上的点投影到图像平面上，这个过程是非线性的。
下图表示出了鱼眼相机的成像过程：

我们知道，普通相机成像遵循的是针孔相机模型，在成像过程中实际场景中的直线仍被投影为图像平面上的直线。但是鱼眼相机如果按照针孔相机模型成像的话，投影图像会变得非常大，当相机视场角达到180°时，图像甚至会变为无穷大。所以，鱼眼相机的投影模型为了将尽可能大的场景投影到有限的图像平面内，允许了相机畸变的存在。并且由于鱼眼相机的径向畸变非常严重，所以鱼眼相机主要的是考虑径向畸变，而忽略其余类型的畸变。

4、畸变模型

畸变模型有径向畸变、切向畸变、等距畸变

4.1、径向畸变

顾名思义，径向畸变就是沿着透镜半径方向分布的畸变，产生原因是光线在原理透镜中心的地方比靠近中心的地方更加弯曲，这种畸变在普通廉价的镜头中表现更加明显，径向畸变的效应有三种，一种是桶形畸变（barrel distortion），另一种是枕形畸变（pincushion distortion），还有一种是两种的结合叫做胡子畸变（mustache distortion），从图片中可以很容易看出区别，具体见下图

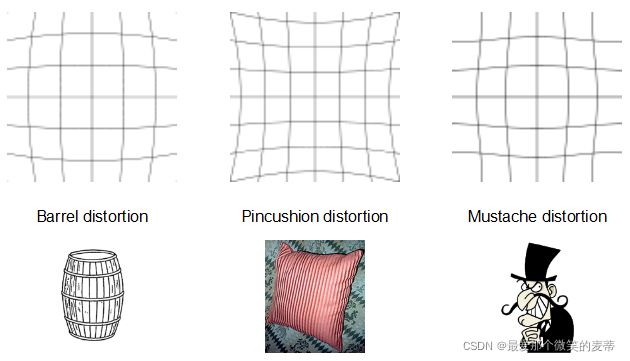
实际情况中我们常用r=0处的泰勒级数展开的前几项来近似描述径向畸变，矫正径向畸变前后的坐标关系为：

4.2、切向畸变

切向畸变是由于透镜本身与相机传感器平面（像平面）或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。畸变模型可以用两个额外的参数p1和p2来描述：

其中，

所以，我们一共需要5个畸变参数(k1,k2,k3,p1,p2)来描述透镜畸变。

综上所述，相机标定实际上就是确定相机的内外参数、畸变参数的过程。

参考文章

https://blog.csdn.net/qq_28087491/article/details/107965151 常用相机投影及畸变模型（针孔|广角|鱼眼）

Tips

相机模型和畸变模型在持续整理中…