（学习笔记）图像处理——高斯滤波、高斯模糊、高斯锐化

概念

一种根据高斯函数的形状来选择权值的线性平滑滤波器，适用于高斯噪声的滤除，在图像处理中应用广泛。高斯滤波是指用高斯函数作为滤波函数，如果高斯低通则是高斯模糊，如果高通则是高斯锐化。

高斯原理

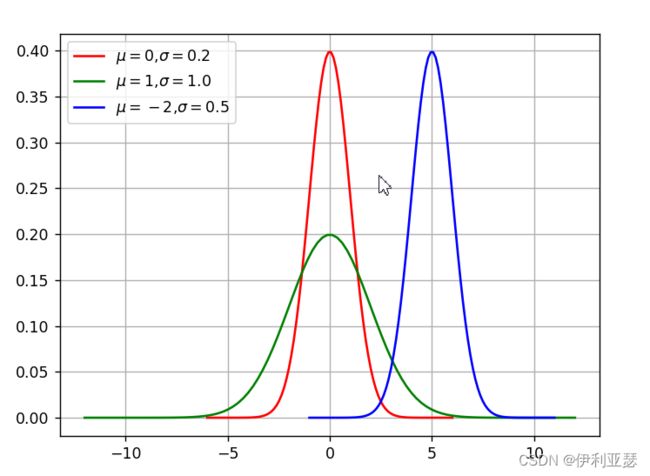
高斯函数:$G(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$得到。
由此可见，G(x)的取值和$\sigma$的大小有关，是如下一种正态分布的关系：

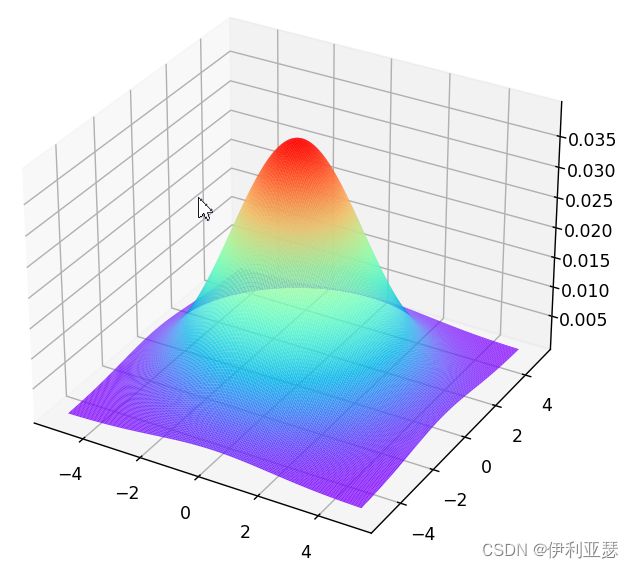
二维高斯函数：$G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{(x-\mu {)}^2+(y-\mu )2}{2{\sigma }^2}}$
其二维图如下所示，可见随着标准差越小图像越窄，标准差越大图像越宽，滤波效果便明显。

高斯模板： 高斯模板是通过高斯函数计算得到的。
取高斯核为3*3，$\mu =0$，$\sigma =0.8$,
高斯模板坐标如下：

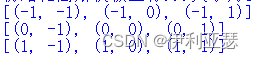
显然，取中心点为初始坐标。计算得高斯矩阵为小数，如下：

这九个点的权重之和为0.9125991675297028，而不为1，因此需要对其进行归一化操作，对每个值都除以0.9125991675297028，最终得到权重矩阵为：

最后将其调整成整数并进行加权处理，具体方法为：首先将左上角第一位数字设置为1，然后其它位数字除以该数并取整，最后除以这些数值之和。得到结果如下：
$$\frac{1}{16}[\begin{array}{ccc}1& 2& 1\\ 2& 4& 2\\ 1& 2& 1\end{array}]$$

当高斯核为5*5，$\mu =0$，$\sigma =2.0$时得到模板坐标如下：

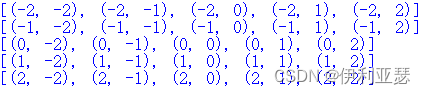
对应的高斯矩阵：

归一化后的权重矩阵为：

同样对其调整加权得到如下：
$$\frac{1}{34}[\begin{array}{ccccc}1& 1& 1& 1& 1\\ 1& 2& 2& 2& 1\\ 1& 2& 2& 2& 1\\ 1& 2& 2& 2& 1\\ 1& 1& 1& 1& 1\end{array}]$$

高斯滤波

高斯滤波是一种低通滤波器，可以滤去低频能量（如噪声），起到平滑图像的作用。
具体操作： 用高斯模板扫描图像中的每一个像素，对于模板中心像素点的值用模板确定的领域内像素的加权平均灰度值去替代。
高斯滤波一般有两种实现方式：离散化窗口滑窗卷积和通过傅里叶变换。一般使用滑窗卷积，只有当窗口相当大，计算量大的情况下考虑傅里叶变换方法。
离散化窗口滑窗卷积： 由于高斯函数可以写成分离形式，因此可通过分离滤波器实现加速，就是将多维卷积化为多个一维卷积，在二维高斯滤波中首先对行做一维卷积，然后对列作一维卷积，这样便能降低计算复杂度。

高斯模糊（高斯平滑）

是图像处理的一种常用技术，主要用来降低图像的噪声并减少图像的细节。原理通俗可理解为：中心像素的像素值为周围像素的像素值的和的平均值。高斯模糊是低通滤波的一种，滤波函数是低通高斯函数，会减少图像的高频信息。
原理： 所有点都取周围点像素的平均值显然不合理，所以高斯模糊通过正态分布的高斯函数来分配周围像素的权重，越接近中心的位置取值越大，远离中心的位置取值越小。在计算时将像素中心作为原点，其他点按高斯函数分配权重，便得到一个加权平均值。这个权重就是高斯模板，高斯模糊就是将（灰度）图像I 和一个高斯模板进行卷积操作：
$$I_{\sigma }=I\ast G_{\sigma }$$
其中，$\ast$表示卷积操作，$G_{\sigma }$是标准差为$\sigma$的高斯模板。

高斯模糊处理图像代码如下：

import cv2
import numpy as np

##gauss filter
def gaussian_filter(img, K=3, sigma=0.8):
    if len(img.shape) == 3:
           H, W, C = img.shape
           #h是高，w是宽，c是通道
    else:
        img = np.expand_dims(img, axis=-1)
        H, W, C = img.shape

    pad = K // 2
    out = np.zeros((H + pad * 2, W + pad * 2, C), dtype=np.float)
    out[pad: pad + H, pad: pad + W] = img.copy().astype(np.float)
    G = np.zeros((K, K), dtype=np.float)

 ##gauss
    for x in range(-pad, -pad + K):
        for y in range(-pad, -pad + K):
            G[y + pad, x + pad] = np.exp( -(x ** 2 + y ** 2) / (2 * (sigma ** 2)))
    G /= (2 * np.pi * sigma * sigma)
    G /= G.sum()
    tmp = out.copy()
	
    for y in range(H):
        for x in range(W):
            for c in range(C):
                out[pad + y, pad + x, c] = np.sum(G * tmp[y: y + K, x: x + K, c])
    out = np.clip(out, 0, 255)
    out = out[pad: pad + H, pad: pad + W].astype(np.uint8)
    return out

# Read image
img = cv2.imread("D:/gauss_blur/2.jpg")
 
# Gaussian Filter
out = gaussian_filter(img, K=3, sigma=0.8)
 
# Save result
cv2.imwrite("D:/gauss_blur/out_1.jpg", out)

#show result
cv2.imshow("result", out)
cv2.imshow("image", img)
cv2.waitKey(0)
cv2.destroyAllWindows()

对同一张图片取不同的窗口k和$\sigma$可得到模糊效果如下：

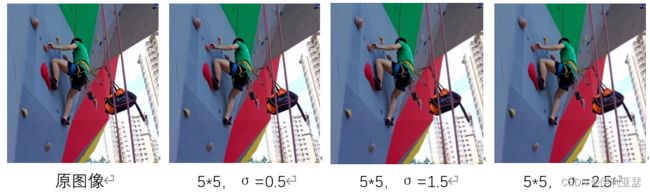
看着不太明显？那我们换张图片并放大窗口到15*15，$\sigma =2.5$试一试效果：

高斯锐化

一种高通高斯滤波器，与低通滤波方法上的不同之处在于，低通滤波让原图像直接与高斯模板进行卷积，而高通滤波让原图像与（1-高斯模板）进行卷积。即：
$$I_{\sigma }=I\ast (1-G_{\sigma })$$
实现代码如下：

import numpy as np
import matplotlib.pyplot as plt
import cv2

class ProcessImg(object):
    def __init__(self, img, sigma):
        self.img = img
        self.sigma = sigma
##锐化
    def sharpen_img(self):
        """image sharpen"""
        kernel = np.array([[0,-1,0],[-1,5,-1],[0,-1,0]], np.float32)
        img_sharpen = cv2.filter2D(self.img, -1, kernel=kernel)
        plt.imshow(img_sharpen.astype(np.int32)[:, :, ::-1])
        plt.show()
        # cv2.imwrite(save_path  + 'sharp_img.png', img_sharpen)
##读取图像并显示
img = cv2.imread('D:/gauss_blur/2.jpg')
plt.imshow(img.astype(np.int32)[:, :, ::-1])
plt.show()
A = ProcessImg(img, 3.0)
A.sharpen_img()

$\sigma =3.0$， 实验结果如下：
原图像：

锐化图像：

原图像：

锐化图像：

个人学习笔记分享，错误望请指正！