李宏毅机器学习2020课后作业笔记 【hw2】 收入分类

1. 问题描述

判断收入是否超过50000，数据集有一些特征，比如说教育背景、出生地之类，是一个二分类的问题，数据集来源Census-Income (KDD) Dataset 本来是有train.csv, test_no_label.csv，但是助教已经帮忙做好了one-hot编码，所以我们拿到的数据是X_train, Y_train, X_test，感觉一下子就简单了不少。没处理前的数据大概长这样。

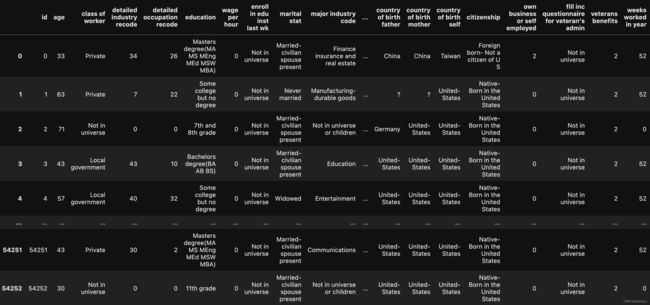
2. 数据预处理

如果是离散特征就用one hot编码排到后面去拼起来，如果是连续的数值，就不用动它

1. 首先，分别标准化一下，标准化函数如下，可以在分母上加一个eps避免除0

# 标准化，大多做预处理都会做这一步的
def _normalize(X, train = True, specified_column = None, X_mean = None, X_std = None):
    if specified_column == None:
        specified_column = np.arange(X.shape[1])
#         print(specified_column)
        # 0 - 509 去掉了第一列id
    if train:
        # np.mean(x, axis=0) 列求平均值，reshape(1, -1)拉成一行
        X_mean = np.mean(X[:, specified_column], 0).reshape(1, -1)
        X_std = np.std(X[:, specified_column], 0).reshape(1, -1)
    # (54256, 510) = (54256, 510) - (1, 510) / (1, 510)
    # 利用了广播的机制
    X[:, specified_column] = (X[:, specified_column] - X_mean) / (X_std + 1e-8)
    
    return X, X_mean, X_std

这里不要用循环，不然计算超级慢，用广播机制。

X_train, X_mean, X_std = _normalize(X_train, train=True)
X_test, _, _ = _normalize(X_test, train=False, specified_column=None, X_mean=X_mean, X_std=X_std)

2. 分割训练集测试集，75% + 25%
   

3. 模型构建与训练

构建标准的$mini-batch$逻辑回归模型，逻辑回归是做分类，线性回归是做预测。
训练前得首先$shuffle$一下数据，$shuffle$自己实现的方法如下

def _shuffle(X, Y):
    randomize = np.arange(len(X))
    np.random.shuffle(randomize)
    return (X[randomize], Y[randomize])

模型构建的关键代码如下，一次取出一个$batch$的样本进行训练，同时存下损失值

for epoch in range(max_iter):
    # 每个epoch先shuffle
    X_train, Y_train = _shuffle(X_train, Y_train)
    
    # Mini-batch training
    for idx in range(int(np.floor(train_size / batch_size))):
        # 每次拿出来一个batchsize
        X = X_train[idx * batch_size : (idx + 1) * batch_size]
        Y = Y_train[idx * batch_size : (idx + 1) * batch_size]
        
        # 梯度更新
        w_grad, b_grad = _gradient(X, Y, w, b)
        
        w -= learning_rate / np.sqrt(step) * w_grad
        b -= learning_rate / np.sqrt(step) * b_grad
        
        step += 1
    y_train_pred = _f(X_train, w, b)
    Y_train_pred = np.round(y_train_pred)
    train_acc.append(_accuracy(Y_train_pred, Y_train))
    train_loss.append(_cross_entropy_loss(y_train_pred, Y_train) / train_size)
    
    y_dev_pred = _f(X_dev, w, b)
    Y_dev_pred = np.round(y_dev_pred)
    dev_acc.append(_accuracy(Y_dev_pred, Y_dev))
    dev_loss.append(_cross_entropy_loss(y_dev_pred, Y_dev) / dev_size)

4. 评估与预测

通过几个自己实现的函数进行预测、评估，其中，$np.clip$第一次用，给两个阈值，超出范围的设定为最大的，小于最小的就令它为下界值。

# sigmoid函数
def _sigmoid(z):
    # np.clip把最小的置为1e8,最大的置为1-1e-8
    return np.clip(1 / (1.0 + np.exp(-z)), 1e-8, 1 - (1e-8))

def _f(X, w, b):
    return _sigmoid(np.matmul(X, w) + b)

def _predict(X, w, b):
    return np.round(_f(X, w, b)).astype(np.int)

def _accuracy(Y_pred, Y_label):
    acc = 1 - np.mean(np.abs(Y_pred - Y_label))
    return acc

最终训练集的准确率在88.5%，测试集合的准确绿率大概87.6%。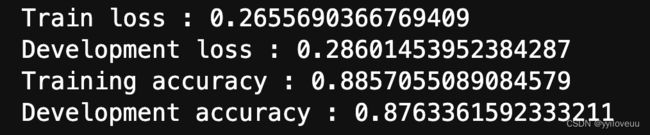先做预测，再保存数据

# predict
# 先预测，再保存数据
predictions = _predict(X_test, w, b)
with open(output_fpath.format('logistic'), 'w') as f:
    f.write('id,label\n')
    for i, label in enumerate(predictions):
        f.write('{},{}\n'.format(i, label))

5. 个人总结

1. $mini-batch$逻辑回归实战
2. 学到一些基本函数的用法，比如$np.clip,np.round,np.random.shuffle$，以及广播机制。