关联规则 Association rules

什么是关联规则

 在数据挖掘中，最终的结果就是要大量的数据中通过算法搜索隐藏于其中信息，有点“在人群中低头找黄金”的意思，那么关联规则(Association Rules)是反映一个事物与其他事物之间的相互依存性和关联性，是数据挖掘的一个重要技术，用于从大量数据中挖掘出有价值的数据项之间的相关关系。废话太多，简单的理解就是 从数据集中寻找物品之间的隐含关系，这种关系并没有在数据中直接表示出来。

定义介绍

  关联规则有一个特别经典的故事：

 沃尔玛的啤酒和尿布的故事。沃尔玛拥有世界上最大的数据仓库系统，为了能够准确了解顾客在其门店的购买习惯，沃尔玛对其顾客的购物行为进行购物篮分析，想知道顾客经常一起购买的商品有哪些。沃尔玛数据仓库里集中了其各门店的详细原始交易数据。在这些原始交易数据的基础上，沃尔玛利用数据挖掘方法对这些数据进行分析和挖掘。一个意外的发现是：“跟尿布一起购买最多的商品竟是啤酒！”经过大量实际调查和分析，揭示了一个隐藏在“尿布与啤酒”背后的美国人的一种行为模式：在美国，一些年轻的父亲下班后经常要到超市去买婴儿尿布，而他们中有30%～40%的人同时也为自己买一些啤酒。产生这一现象的原因是：美国的太太们常叮嘱她们的丈夫下班后为小孩买尿布，而丈夫们在买尿布后又随手带回了他们喜欢的啤酒

 在这样的一个传统的购物篮场景，若两个或多个变量的取值之间存在某种规律性，就称为关联，关联规则挖掘出了形如 由于某些事件的发生而引起另外一些事件的发生之类的规则，但是，大家一定要注意到，关联规则不是因果关系 （有可能有因果关系 , 有可能没有 ），就比如说 购买商品时 , 啤酒 与 尿布 就有关联关系 , 这两个之间肯定没有因果关系 , 有一种未知的关联关系 。并不是说，买了啤酒才会买尿布;

 我们需要简单介绍一下关联规则设计到的基本概念：

• 项目与项集

  • 项目： 数据库中不可分割的最小单位信息，称为项目，用符号i表示，熟悉数据库的同学可以理解到项目其实是数据库里的一个字段，比如说在超市交易数据库来说，项目就是一次交易中的一个物品，比如：牛奶。
  • 项集：包含若干个项目的集合（一次事务中的），一般会大于0个，比如说：多少个牛奶，设集合I={i1, i2, ..., ik}是项集，I中项目的个数为k，则集合I称为k-项集。可以理解为你的购物车里买了几种东西

• 事务：设I={i1, i2, ..., ik}是由数据库中所有项目构成的集合，一次处理所含项目的集合用T表示，T={t1, t2, ..., tn}。每一个包含ti子项的项集都是I子集，可以理解为你有几个购物车。

• 项集的频数（支持度计数）：包括项集的事务数称为项集的频数（支持度计数）。

• 关联规则：关联规则是形如X=>Y的蕴含式，其中 X、Y 分别是项集，并且X∩Y=Ø。X 称为规则前项（antecedent），Y 称为规则后项（consequent）。关联规则反映 X 中的项目出现时，Y 中的项目也跟着出现的规律。

• 支持度（support）：几个关联的数据在数据集中出现的次数占总数据集的比重
  
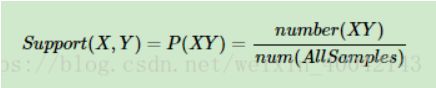
  支持度 = （包含物品 X 的记录数量） / （总的记录数量），支持度是一个百分比，可以理解成商品的流行程度，或者说是商品X与商品Y之间的配比度 ，支持度越高，代表这个组合出现的概率，或者配比度越高。我们举一个例子来说：在一次的购买记录中，牛奶的支持度为：牛奶在N次交易中出现的次数 / 交易的总次数，即3/5。(支持度不仅可以统计两个物品同时出现的概率，也可以统计单个商品的概率)，（牛奶和鸡蛋）的支持度为：牛奶与鸡蛋一起出现的订单次数 / 交易总次数。

• 置信度（confidence ）：一个数据出现后，另一个数据出现的概率，或者说数据的条件概率。
  
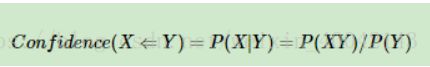
  置信度( X -> Y) = （包含物品 X 和 Y 的记录数量） / （包含 X 的记录数量），置信度是个条件概念，就是说在 X 发生的情况下, Y 发生的概率是多少。即就是当你购买了商品 X，会有多大的概率购买商品 Y。表示关联性的强弱，或者说是规则的可靠性， 例如，(牛奶→啤酒)一起购买的次数是2，（牛奶）的购买次数是4次，置信度（牛奶→啤酒）=2/4=0.5，代表如果你购买了牛奶，有50%的概率会购买啤酒。

• 提升度（lift）：表示含有Y的条件下，同时含有X的概率，与X总体发生的概率之比
  
  提升度( X -> Y) = 置信度( X -> Y) / (支持度 X)，提升度当销售一个物品时，另一个物品销售率会增加多少，比如说：Confidence(牛奶->鸡蛋)=2 / 4。Support(牛奶)=3 / 5，那么我们就能计算牛奶和鸡蛋的支持度Lift(牛奶->鸡蛋)=0.83。提升度有三种可能性：

  • 提升度 (X→Y) > 1：代表有提升；说明 X 卖的越多， Y 卖的就越多。关联性就越强
  • 提升度 (X→Y) = 1：代表有没有提升，也没有下降；说明 X 和 Y 之间没有关联。两者是相互对立的
  • 提升度 (X→Y) < 1：代表有下降。说明购买 X 反而会减少 Y 的销量。

• 最小支持度与最小置信度

  通常用户为了达到一定的要求，需要指定规则必须满足的支持度和置信度阈限，当support(X=>Y)、confidence(X=>Y)分别大于等于各自的阈限值时，认为X=>Y是有意义的，此两个值称为最小支持阈值(min_sup)和最小置信阈值(min_conf)。其中，min_sup描述了关联规则的最低重要程度，min_conf规定了关联规则必须满足的最低可靠性。

• 频繁项集

  设U={u1, u2, …, un}为项目的集合，且UI，U≠Ø，对于给定的最小支持度min_sup，如果项集U的支持度support(U)≧min_sup，则称U为频繁项集，否则，U为非频繁项集。

• 强关联规则

  support(X=>Y)≧min_sup且confidence(X=>Y)≧min_conf，称关联规则X=>Y为强关联规则，否则为弱关联规则。

关联规则算法

 因为选择物品之间的关联规则就是要寻找物品之间的潜在关系，那么应该如何寻找物品之间的潜在关系

1. 第一步就是从哪里寻找——频繁项集，找出频繁出现的物品集的集合。即找出满足最小支持度的所有项集
2. 第二步就是找什么——在频繁项集的基础上，我们通过关联规则算法找出其中物品的关联结果。即从频繁项集中提取所有高置信度的规则

 简单的来说，就是先找频繁项集，再根据关联规则找关联物品，关联规则中，比较关键的两个点是：（1）三种阈值的设定（2）如何找出频繁项集。

 那么使用关联规则的过程主要是四个步骤：

1. 数据筛选，首先对数据进行清洗，清洗掉那些公共的项目，比如：热门词，通用词（此步依据具体项目而定）
2. 根据支持度（support），从事务集合中找出频繁项集（使用算法：Apriori算法，FP-Growth算法）
3. 根据置信度（confidence），从频繁项集中找出强关联规则（置信度阈值需要根据实验或者经验而定）
4. 根据提升度（lift），从强关联规则中筛选出有效的强关联规则（提升度的设定需要经过多次试验确定）

 简单的来说，关联规则的算法背景就是

 已知支持度计算公式 -> 遍历所有组合 -> 计算其支持度 -> 筛选出大于最小支持度（阈值）的组合 -> 从中筛选出频繁项 ->计算置信度 -> 找出强关联规则 -> 计算提升度 -> 找到关联规则

 那么这样出现了问题——遍历所有组合的计算机是在太大了

Apriori算法

 关联规则挖掘算法是关联规则挖掘研究的主要内容，迄今为止已提出了许多高效的关联规则挖掘算法。最著名的关联规则发现方法是R.Agrawal提出的Apriori算法。

 Apriori算法是最经典的挖掘频繁项集的方法。

Apriori原理

 既然Apriori算法的核心是识别或者发现所有频繁项目集，因为我们都根据上面的定义公式就可以知道，一个物品的支持度越大，那么这个物品其实就越受欢迎。

• 如果一个项集是频繁项集，则它的所有子集都是频繁项集
• 如果一个集合不是频繁项集，则它的所有父集（超集）都不是频繁项集

 Apriori的优势就在于，它并不需要遍历所有的组合。就比如说，假设（AB）为非频繁集，那么虚线框内的它的超集都是非频繁集。这样的话，很多的组合都被去掉了，也就是不用遍历所有的组合了。

连接步和剪枝步

  Apriori 算法采用连接步和剪枝步两种方式来找出所有的频繁项集。

1. 连接步

   连接步的目的是找到K项集。对给定的最小支持度阈值，分别对1项候选集C₁ ，剔除小于该阈值的项集得到1项频繁集L₁；下一步有L₁自身连接产生2项候选集C₂，保留C₂中满足约束条件的项集得到2项频繁集，记为L₂；再下一步 有L₂与L₃连接产生3项候选集C₃，保留C₂中 满足约束条件的项集得到3项频繁集，记为L₃…这样循环下去，得到最大频繁项集L_k

2. 剪枝步

   剪枝步紧接着连接步，在产生候选项C_k的过程中起到减小搜索空间的目的。由于C_k是L_k-1与L_k连接产生的，根据Apriori的性质，不是频繁项目集不会存在于C_k中，该过程就是剪枝。

 Apriori 算法使用使用一种称作逐层搜索的迭代方法， k 项集用于探索 (k+1) 项集。首先，搜索出候选1项集及对应的支持度，剪枝去掉低于支持度的1项集，得到频繁1项集。然后对剩下的频繁1项集进行连接，得到候选的频繁2项集，筛选去掉低于支持度的候选频繁2项集，得到真正的频繁二项集，以此类推，迭代下去，直到无法找到频繁k+1项集为止，对应的频繁k项集的集合即为算法的输出结果。

 第 i 次的迭代过程包括扫描计算候选频繁 i 项集的支持度，剪枝得到真正频繁 i 项集和连接生成候选频繁 i+1 项集三步。

实例解释

TID	Items
1	{1 3 4}
2	{ 2 3 5 }
3	{1 2 3 5}
4	{2 5}

我们的数据集D有4条记录，分别是{1,3,4},{2,3,5},{1,2,3,5},{2,5}，在这里我们设置最小支持度阈值（min_sup）为50%

1. 针对数据集生成频繁1项集,并计算其支持度

itemset	出现次数	suport
{1}	2	2/4
{2}	3	3/4
{3}	3	3/4
{4}	1	1/4
{5}	3	3/4

 减去支持度<0.5的项集，那么就剩下{1},{2},{3},{5}

2. 生成频繁2项集，（根据步骤1剩下的项生成）

itemset
{1,2}
{1,3}
{1,5}
{2,5}
{3,5}

 此时第一轮迭代结束了

3. 进入第二轮迭代

itemset	出现次数	support
{1,2}	1	1/4
{1,3}	2	2/4
{1,5}	1	1/4
{2,3}	2	2/4
{2,5}	3	3/4
{3,5}	2	2/4

 排除<0.5的支持度的项集，剩下的{1,3},{2,3},{2,5},{3,5}

4. 生成频繁3项集

 {1,2,3},{1,2,5},{1,3,5},{2,3,5}此时第二轮迭代结束

5. 进入第三轮迭代

itemset	出现次数	support
{1,2,3}	1	1/4
{1,2,5}	2	2/4
{1,3,5}	1	1/4
{2,3,5}	1	1/4

 排除<0.5的项集，剩下的 {2,3,5}

6. 此时数量为3不支持生成频繁4项集，迭代结束。

7. 由频繁集产生关联规则——根据置信度公式得出

 Apriori算法的两个输入参数分别是最小支持度和数据集，该算法首先会生成所有单个元素的项集列表。接着扫描数据集来查看哪些项集满足最小支持度要求，那些不满足最小支持度的集合会被去掉，然后，对剩下来的集合进行组合以生成包含两个元素的项集，接下来，再重新扫描交易记录，去掉不满足最小支持度的项集。该过程重复进行直到所有项集都被去掉

代码实现

import pandas as pd
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori

# 设置数据集

dataset = [['牛奶','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'],
        ['莳萝','洋葱','肉豆蔻','芸豆','鸡蛋','酸奶'],
        ['牛奶','苹果','芸豆','鸡蛋'],
        ['牛奶','独角兽','玉米','芸豆','酸奶'],
        ['玉米','洋葱','洋葱','芸豆','冰淇淋','鸡蛋']]

te = TransactionEncoder()
# 进行one-hot编码
'''
首先，需要先将商品进行one-hot编码，编码后用boolean值表示。
所谓ont-hot编码呢，直观来说就是有多少个状态就有多少比特，而且只有一个比特为1，其他全为0的一种码制。
比如冰淇淋只存在最后一共交易单中，其他交易中都没出现。那冰淇淋就可以用[0,0,0,0,1]来表示
'''

te_ary = te.fit(rescords).transform(rescords)
df = pd.DataFrame(te_ary,columns=te.columns_)

# 利用 Apriori
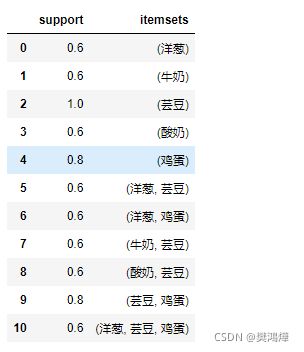
freq = apriori(df,min_support=0.6,use_colnames=True) 

# 输出一下freq

# 规则
from mlxtend.frequent_patterns import association_rules
result = association_rules(freq,metric="confidence",min_threshold=0.6)
# DataFrame排序 
result.sort_values(by = ['confidence','lift'],ascending=False,axis=1)
# 输出一下result

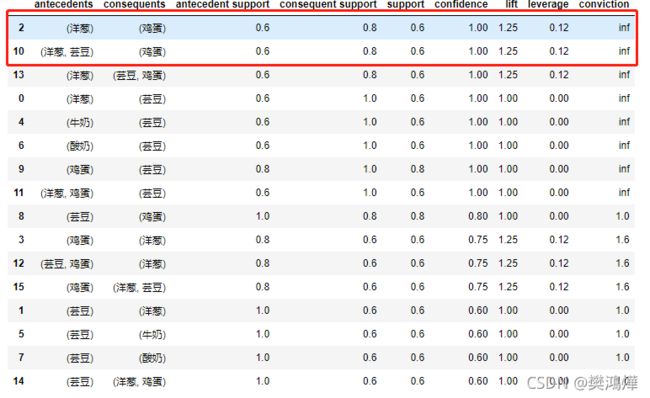
 上面例子中我们可以发现，{洋葱 -> 鸡蛋,芸豆} 的置信度是 1.00 ，而它们的提升度是 1.25 。这说明买了洋葱的人很可能会再购买 1.25 份的 {鸡蛋,芸豆} 。所以可以让它们放到一起出售。

 Aprior算法是一个非常经典的频繁项集的挖掘算法，很多算法都是基于Aprior算法而产生的，包括FP-Tree,GSP, CBA等。这些算法利用了Aprior算法的思想，但是对算法做了改进，数据挖掘效率更好一些，因此现在一般很少直接用Aprior算法来挖掘数据了，但是理解Aprior算法是理解其它Aprior类算法的前提，同时算法本身也不复杂，因此值得好好研究一番。

FP-Tree算法

 经典的关联规则挖掘算法包括Apriori算法和FP-Tree算法。apriori算法多次扫描交易数据库(I/O是很大的瓶颈)，每次利用候选频繁集产生频繁集；而FP-Tree则利用树形结构，无需产生候选频繁集而是直接得到频繁集，大大减少扫描交易数据库的次数，从而提高了算法的效率。但是apriori的算法扩展性较好，可以用于并行计算等领域。

 使用Apriori算法进行关联分析。FP-Tree算法来高效发现频繁项集。

FP-Tree原理结构

 FP Tree算法（也称FP Growth算法）采用了一些技巧，无论多少数据，只需要扫描两次数据集，　　　　为了减少I/O次数，FP Tree算法引入了一些数据结构来临时存储数据。这个数据结构包括三部分，如下图所示：

• 第一部分是一个项头表。里面记录了所有的1项频繁集出现的次数，按照次数降序排列。比如上图中B在所有10组数据中出现了8次，因此排在第一位。
• 第二部分是FP Tree，它将我们的原始数据集映射到了内存中的一颗FP树。
• 第三部分是节点链表。所有项头表里的1项频繁集都是一个节点链表的头，它依次指向FP树中该1项频繁集出现的位置

 那么问题来了，FP Tree是怎么建立的呢？节点链表存在的意义是什么？这样做主要是方便项头表和FP Tree之间的联系查找和更新，也好理解。

项头表的建立

 根据上面的叙述，我们可以发现FP树的建立需要首先依赖项头表的建立。

 它的大致步骤是这样的：我们第一次扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。接着第二次也是最后一次扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列。

 例子来具体讲解。我们有10条数据，首先第一次扫描数据并对1项集计数，我们发现O，I，L，J，P，M, N都只出现一次，支持度低于20%的阈值，因此他们不会出现在下面的项头表中。剩下的A,C,E,G,B,D,F按照支持度的大小降序排列，组成了我们的项头表。

 接着我们第二次扫描数据，对于每条数据剔除非频繁1项集，并按照支持度降序排列。比如数据项ABCEFO，里面O是非频繁1项集，因此被剔除，只剩下了ABCEF。按照支持度的顺序排序，它变成了ACEBF。其他的数据项以此类推。

  为什么要将原始数据集里的频繁1项数据项进行排序呢？这是为了我们后面的FP树的建立时，可以尽可能的共用祖先节点。

 通过两次扫描，项头表已经建立，排序后的数据集也已经得到了，下面我们再看看怎么建立FP树

FP Tree的建立

 有了项头表和排序后的数据集，我们就可以开始FP树的建立了。开始时FP树没有数据，建立FP树时我们一条条的读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。

 我们来举例说明：

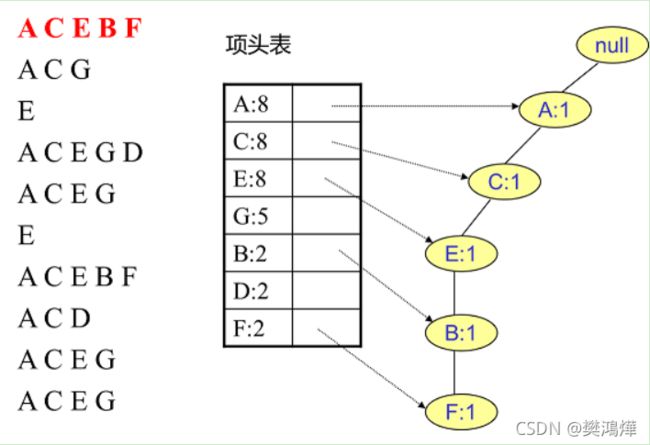
 首先，我们插入第一条数据ACEBF，如下图所示。此时FP树没有节点，因此ACEBF是一个独立的路径，所有节点计数为1, 项头表通过节点链表链接上对应的新增节点。
　
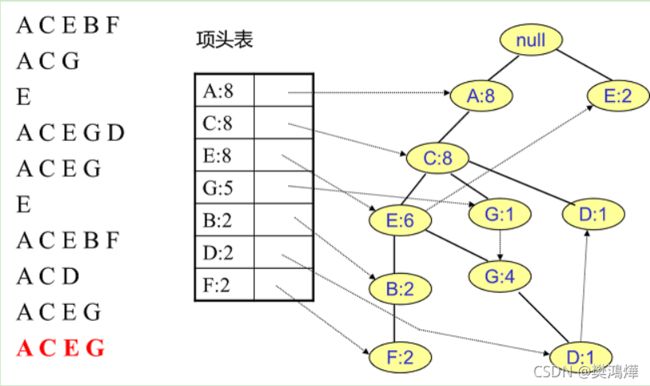
 接着我们插入数据ACG，如下图所示。由于ACG和现有的FP树可以有共有的祖先节点序列AC，因此只需要增加一个新节点G，将新节点G的计数记为1。同时A和C的计数加1成为2。当然，对应的G节点的节点链表要更新。

 同样的办法可以更新后面8条数据，最终结果如下图：

FP Tree的挖掘

 通过上面的步骤 ，我们得到了FP树和项头表以及节点链表，我们首先要从项头表的底部项依次向上挖掘。对于项头表对应于FP树的每一项，我们要找到它的条件模式基。

 所谓条件模式基是以我们要挖掘的节点作为叶子节点所对应的FP子树。得到这个FP子树，我们将子树中每个节点的的计数设置为叶子节点的计数，并删除计数低于支持度的节点。从这个条件模式基，我们就可以递归挖掘得到频繁项集了。

 还是举例子来说吧：

 我们继续上面的步骤，看看先从最底下的F节点开始，我们先来寻找F节点的条件模式基，由于F在FP树中只有一个节点，因此候选就只有下图左所示的一条路径，对应{A:8,C:8,E:6,B:2, F:2}。我们接着将所有的祖先节点计数设置为叶子节点的计数，即FP子树变成{A:2,C:2,E:2,B:2, F:2}。一般我们的条件模式基可以不写叶子节点，因此最终的F的条件模式基如下图右所示。

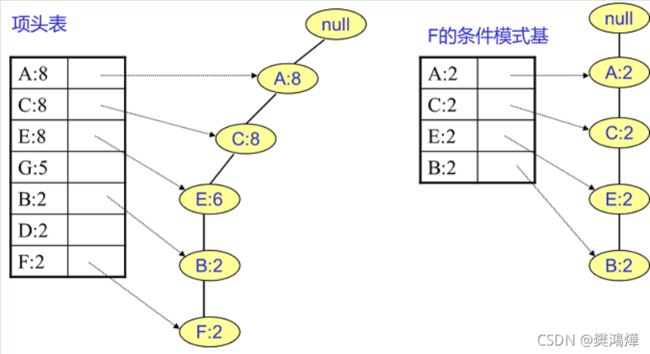
 通过它，我们很容易得到F的频繁2项集为{A:2,F:2}, {C:2,F:2}, {E:2,F:2}, {B:2,F:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,F:2}，{A:2,E:2,F:2},.…还有一些频繁三项集，就不写了。当然一直递归下去，最大的频繁项集为频繁5项集，为{A:2,C:2,E:2,B:2,F:2}

 F挖掘完了，我们开始挖掘D节点。D节点比F节点复杂一些，因为它有两个叶子节点，因此首先得到的FP子树如下图左。我们接着将所有的祖先节点计数设置为叶子节点的计数，即变成{A:2, C:2,E:1 G:1,D:1, D:1}此时E节点和G节点由于在条件模式基里面的支持度低于阈值，被我们删除，最终在去除低支持度节点并不包括叶子节点后D的条件模式基为{A:2, C:2}。通过它，我们很容易得到D的频繁2项集为{A:2,D:2}, {C:2,D:2}。递归合并二项集，得到频繁三项集为{A:2,C:2,D:2}。D对应的最大的频繁项集为频繁3项集。

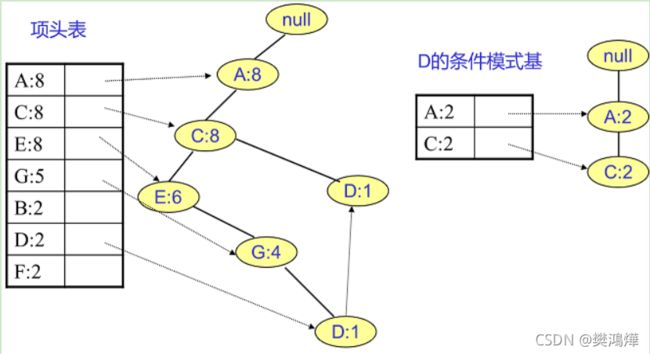
 同样的方法可以得到B的条件模式基如下图右边，递归挖掘到B的最大频繁项集为频繁4项集{A:2, C:2, E:2,B:2}。

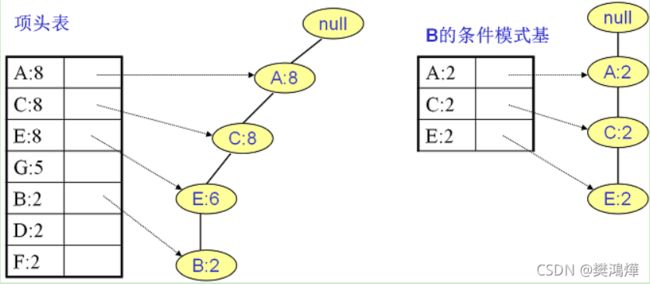
 继续挖掘G的频繁项集，挖掘到的G的条件模式基如下图右边，递归挖掘到G的最大频繁项集为频繁4项集{A:5, C:5, E:4,G:4}。

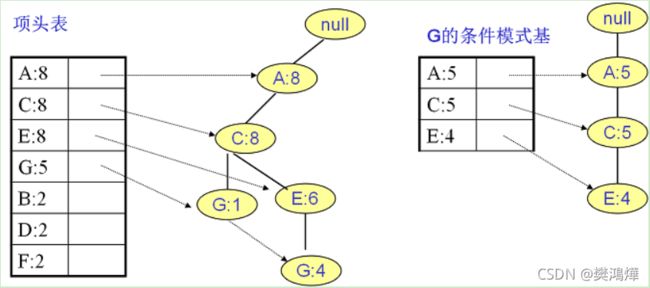
 E的条件模式基如下图右边，递归挖掘到E的最大频繁项集为频繁3项集{A:6, C:6, E:6}。

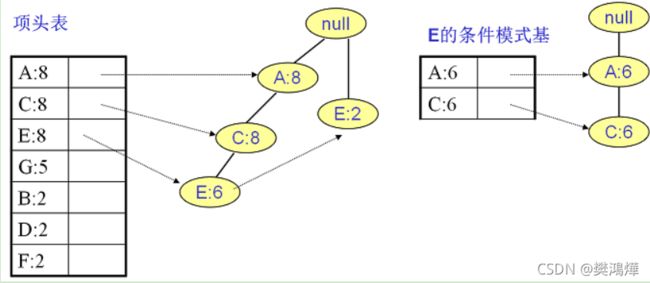
 C的条件模式基如下图右边，递归挖掘到C的最大频繁项集为频繁2项集{A:8, C:8}。

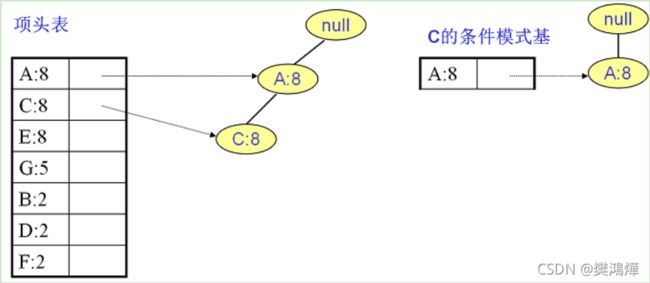
 至于A，由于它的条件模式基为空，因此可以不用去挖掘了。至此我们得到了所有的频繁项集，如果我们只是要最大的频繁K项集，从上面的分析可以看到，最大的频繁项集为5项集。包括{A:2, C:2, E:2,B:2,F:2}。

 根据前面对FP Tree三部分结构的解释，相信大家对此有了一定的了解了，那么这里对整个算法流程做一个归纳：

1. 扫描数据，得到所有频繁一项集的的计数。然后删除支持度低于阈值的项，将1项频繁集放入项头表，并按照支持度降序排列。
2. 扫描数据，将读到的原始数据剔除非频繁1项集，并按照支持度降序排列。
3. 读入排序后的数据集，插入FP树，插入时按照排序后的顺序，插入FP树中，排序靠前的节点是祖先节点，而靠后的是子孙节点。如果有共用的祖先，则对应的公用祖先节点计数加1。插入后，如果有新节点出现，则项头表对应的节点会通过节点链表链接上新节点。直到所有的数据都插入到FP树后，FP树的建立完成。
4. 从项头表的底部项依次向上找到项头表项对应的条件模式基。从条件模式基递归挖掘得到项头表项项的频繁项集。
5. 如果不限制频繁项集的项数，则返回步骤4所有的频繁项集，否则只返回满足项数要求的频繁项集。

 参考文章：

数据挖掘之关联规则(Apriori算法)
Apriori算法原理总结
深入浅出Apriori关联分析算法（一）
Apriori算法和FP-growth算法比较
FP Tree算法原理总结