【python代码实现】人工神经网络分类算法及其实战案例（股票价格波动分析）

前置知识

1、前言

紧接着前面两篇关于分类算法的文章，今天我们来讲一讲人工神经网络分类算法，本文算法代码实现部分的数据与之前两篇一致，大家可自行查看：
【python代码实现】决策树分类算法
【python代码实现】朴素贝叶斯分类算法

2、人工神经网络模型

2.1、神经元模型与单层神经网络

人工神经网络中最基本的成分是神经元模型，也称MP神经元模型。在这个模型中，神经元接收到来自其他神经元传递过来的信息，如图中的箭头称之为连接。连接是神经元中最重要的东西，每一个连接上都有一个权重，输入信号通过带权重的连接进行传递，神经元接收到的总输入值与神经元阀值进行比较，然后通过激活函数处理以产生神经元输出。

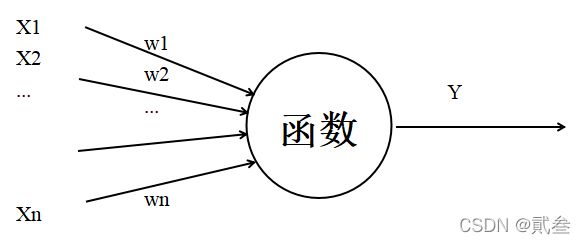
在MP神经元模型的输入位置添加神经元节点，标志其为“输入单元”，输入层的输入单元只负责接收信号后传递给输出层；而输出层的输出单元需要对前面一层的输入进行计算。我们把需要计算的层次称为计算层，并把拥有一个计算层的网络称之为单层神经网络。

2.2、多层人工神经网络模型

单层神经网络本质上是若干个权重与信号的线性组合，无法解决非线性问题。因此在此基础上加入隐含层，发展出可以解决非线性问题的多层神经网络。

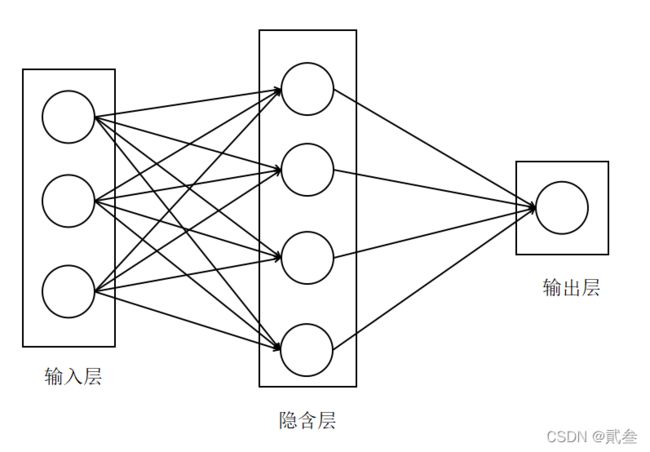
多层神经网络实际上是将多个神经元进行组合，用不同的方法进行连接并作用到激活函数上，一般使用的激活函数是Sigmoid函数。

之所以选用Sigmoid函数，主要是它与正态高斯分布函数图像接近；符合日常生活大多数现象且计算简单，可降低算法计算开销。

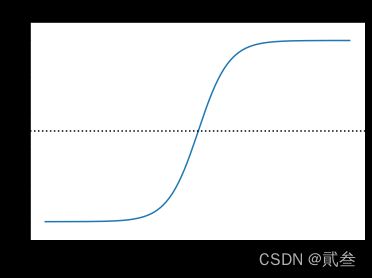
与文章【实战】——以波士顿房价为例进行数据的相关分析和回归分析中逻辑回归部分相似，这里的模型以是否买产品将数据分为0/1类，也就是目标值y；其对应的输入矩阵x与权重矩阵相乘得到另一个数据，称之为预测值y’。预测值与真实值之间的距离越小，损失也越小，模型越准确。

神经网络算法的基本思路是：从随机设置的权重开始，通过网络输出与实际样本之间的误差来调整权重，使得输出样本与样本观测值之间的误差不断减小来完成模型训练。

人工神经网络分类算法

1、构建数据集

# 构建数据集
def createdataset():
    dataSet=[[0,2,0,0,0],
            [0,2,0,1,0],
            [1,2,0,0,1],
            [2,1,0,0,1],
            [2,0,1,0,1],
            [2,0,1,1,0],
            [1,0,1,1,1],
            [0,1,0,0,0],
            [0,0,1,0,1],
            [2,1,1,0,1],
            [0,1,1,1,1],
            [1,1,0,1,1],
            [1,2,1,0,1],
            [2,1,0,1,0],]
    labels=['age','income','job','credit']
    return dataSet,labels

与之前的分类算法不同，这里将数据分类标签‘Y/N’改为了0/1

ds1,lab = createdataset()
x = np.array(ds1)[:,0:4]
y = np.array(ds1)[:,4].reshape(14,1)
print(x)
print(y)

因为后续的计算都是基于二维矩阵的，所以这里将目标值y转化为二维数组。

2、响应函数

# 响应函数
def nonlin(x,deriv=False):
    if(deriv==True):
        return x*(1-x)
    return 1/(1+np.exp(-x))

相应函数充分利用了Sigmoid函数的数学特征，简化了计算

3、模型训练

# 中间层/隐含层系数矩阵
syn0 = np.random.random((4,4))
# 输出层系数
syn1 = np.random.random((4,1))
print('算法开始前，随机系数矩阵：')
print("syn0:",str(syn0))
print("syn1:",str(syn1))

首先，先产生一个随机矩阵作为模型的权重系数矩阵；然后再经过训练得出模型的系数矩阵：

for i in range(1000):
    # 计算误差
    layer0 = x
    layer1 = nonlin(np.dot(layer0,syn0))
    layer2 = nonlin(np.dot(layer1,syn1))
    
    layer2_error = y - layer2
    # 每循环200，输出一次系数矩阵
    if((i+1)%200)==0:
        print("After:",i)
        print("Error:",np.mean(np.abs(layer2_error)))
        print("syn0:\n",syn0)
        print("syn1:\n",syn1)
    # 梯度下降法调整系数矩阵
    layer2_delta = layer2_error*nonlin(layer2,deriv=True)
    layer1_error = layer2_delta.dot(syn1.T)
    layer1_delta = layer1_error*nonlin(layer1,deriv=True)
    
    syn0 += layer0.T.dot(layer1_delta)
    syn1 += layer1.T.dot(layer2_delta)

这里循环1000次，利用梯度下降法调整系数矩阵，使得误差收敛。为了便于观察迭代效果，每运行200输出一次误差Error和系数矩阵：

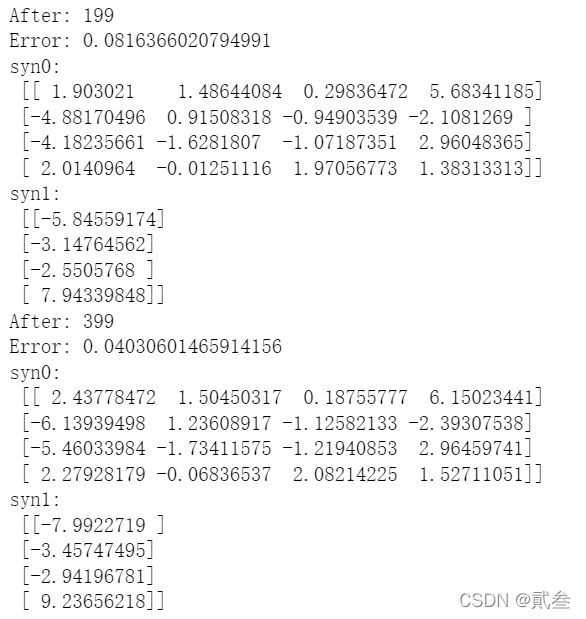
直到循环结束：

到此，我们就已经得到了一个误差为0.02的模型了。

4、测试样本分类

与之前的分类算法一样，我们对新的测试数据进行分类，看结果是否正确：

ly = [0,2,0,1]
ly1 = nonlin(np.dot(ly,syn0))
ly2 = nonlin(np.dot(ly1,syn1))
print("Test input:"+str(ly)+";Test output:"+str(ly2))

Test input:[0, 2, 0, 1];Test output:[0.00784408]

ly0 = [0,0,1,1]
ly01 = nonlin(np.dot(ly0,syn0))
ly02 = nonlin(np.dot(ly01,syn1))
print("Test input:"+str(ly0)+";Test output:"+str(ly02))

Test input:[0, 0, 1, 1];Test output:[0.99941724]

可以看到结果与决策树分类算法、朴素贝叶斯分类算法的结果一致，进一步证明了结果的正确性。

案例：股票价格波动分析

1、数据来源

案例股票是中国平安保险集团股份有限公司（601318），2016-01-01至2020-12-31的开盘价、最高价、最低价、收盘价和日收益率，数据来自锐思金融数据库，共1218个数据。

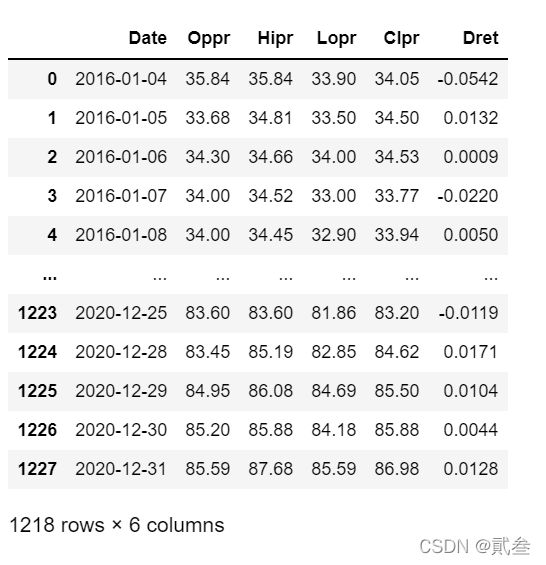
2、变量与指标

输入矩阵由4个基于5天预测时段的收益率（rdp5、rdp10、rdp15、rdp20）和转变后的收盘价（ema15）5个分量组成。

rdpn = (p(i+5 - n) - p(i - n))/p(i - n) * 100
ema15是当天收盘价减去前15天价格指数滑动平均值

输出变量（rdp）是首先分别将当天与其后第5天的原始收盘价转换为各自前3天的指数滑动平均值，在以此求收益率。

指标均方误差（MSE）与平均绝对误差（MAE）用于衡量真实值与预测值之间的偏差度，值越小预测越好。

3、数据处理

模型主要用到的是收盘价，因此将数据提取出来并转化为浮点数：

f1 = csv.reader(open('a601318.csv'))
closeprice = [row[4] for row in f1]
del closeprice[0]
p = list(map(float,closeprice))
len(p)

4、指标计算

计算指标rdp5、rdp10、rdp15、rdp20：

rdp5 = []
for i in range(len(p)):
    if i > 5:
        rdp5.append((p[i]-p[i-5])/p[i-5]*100)
rdp5 = rdp5[14:1211]

rdp10 = []
for i in range(len(p)):
    if i > 10:
        rdp10.append((p[i-5]-p[i-10])/p[i-10]*100)
rdp10 = rdp10[9:1206]

rdp15 = []
for i in range(len(p)):
    if i > 15:
        rdp15.append((p[i-10]-p[i-15])/p[i-15]*100)
rdp15 = rdp15[4:1201]

rdp20 = []
for i in range(len(p)):
    if i > 20:
        rdp20.append((p[i-15]-p[i-20])/p[i-20]*100)

计算指标ema15：

def get_ema(cps,days):
    emas = cps.copy()
    for i in range(len(cps)):
        if i < 15:
            emas[i] = cps[i]
        if i >= 15:
            emas[i] = ((days-1)*emas[i-1]+2*cps[i])/(days+1)
    return emas

ema = get_ema(p,15)
ema15 = [p[i] - ema[i] for i in range(len(p))]
ema15 = ema15[20:1217]

计算指标rdp：

p1 = get_ema(p,3)
rdp = []
for i in range(len(p1)):
    if i < len(p1)-5:
        rdp.append((p1[i+5]-p[i])/p1[i]*100)
rdp = rdp[15:1212]

4、模型训练

构造数据集：

data = pd.DataFrame()
data['rdp5'] = np.array(rdp5)
data['rdp10'] = np.array(rdp10)
data['rdp15'] = np.array(rdp15)
data['rdp20'] = np.array(rdp20)
data['ema15'] = np.array(ema15)
target = pd.DataFrame()
target = np.array(rdp)

将数据集分为训练集测试集：

x_train,x_test,y_train,y_test = train_test_split(data,target,random_state=7,test_size=0.1)
print(len(x_train),len(x_test),len(y_train),len(y_test))
print(y_test[0:5])

模型训练：

mlplr = MLPRegressor(activation='logistic',learning_rate='adaptive')
mlplr.fit(x_train,y_train)

这里构造了多层感知回归器mlplr，它本质上是一个基于人工神经网络的回归方程。使用logistic（Sigmoid）函数作为神经元的激活函数，学习率采用adaptive自适应方式。

5、模型预测及可视化

mlplr_y_predict = mlplr.predict(x_test)
print('MSE：',"%.4f"%mean_squared_error(y_test,mlplr_y_predict))
print('MAE：',"%.4f"%mean_absolute_error(y_test,mlplr_y_predict))

MSE： 0.0365
MAE： 0.1552

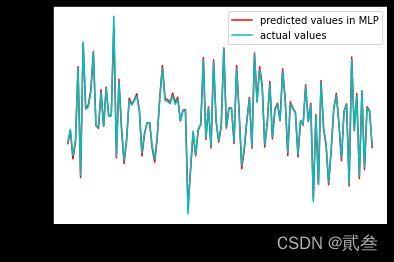
从模型的MSE、MAE来看，测试集的预测数据与实际数据吻合较为理想

point = []
for i in range(len(x_test)):
    a=1+i
    point.append(a)
plt.plot(point,mlplr_y_predict,color='r',linestyle='-',label='predicted values in MLP')
plt.plot(point,y_test,color='c',linestyle='-',label='actual values')
plt.xlabel('Test data points')
plt.ylabel('Normalized target value')
plt.legend()
plt.show()

结语

神经网络的发展非常迅速，其在金融中的股票市场预测、借贷风险管理、信用卡欺骗检测等应用领域取得较好结果。

关于分类算法的文章就讲到这里啦，大家如果觉得文章不错的话，记得收藏、点赞、关注三连~

【python代码实现】决策树分类算法
【python代码实现】朴素贝叶斯分类算法
【python代码实现】人工神经网络分类算法及其实战案例（股票价格波动分析）本文