论文《Efficient Heterogeneous Collaborative Filtering without Negative Sampling for Recommendation》阅读
论文《Efficient Heterogeneous Collaborative Filtering without Negative Sampling for Recommendation》阅读
- 论文概况
- 方法论
- 总结
今天简要介绍论文《Efficient Heterogeneous Collaborative Filtering without Negative Sampling for Recommendation》,论文对推荐系统中需要进行负采样添加负例而造成的性能损失这一问题进行了解决。论文提出了 EHCF 模型,并发表在了 AAAI 2020 (CCF A类会议),由清华大学 THUIR 组完成,论文角度新颖,完成度很高,非常值得推荐。
论文概况
鉴于在 浅谈个性化推荐系统中的非采样学习 这篇文章中已经有了较好的介绍,就不再复述一遍了。这里简要介绍一下本文的工作重点和主要思路,具体细节可以移步下面链接。
浅谈个性化推荐系统中的非采样学习
另外,作者这一工作在不同方向进行扩展,一共完成了四篇顶刊顶会文章的录用。高山仰止,见贤思齐,牛啊!
Chong Chen, Min Zhang, Yongfeng Zhang, Yiqun Liu and Shaoping Ma. Efficient Neural Matrix Factorization without Sampling for Recommendation. ACM Transactions on Information Systems. (TOIS Vol. 38, No. 2, Article 14)
Chong Chen, Min Zhang, Chenyang Wang, Weizhi Ma, Minming Li, Yiqun Liu and Shaoping Ma.An Efficient Adaptive Transfer Neural Network for Social-aware Recommendation.The 42th International ACM SIGIR Conference on Research and Development in Information Retrieval.(SIGIR 2019)
Chong Chen, Min Zhang, Weizhi Ma, Yongfeng Zhang, Yiqun Liu and Shaoping Ma.Efficient Heterogeneous Collaborative Filtering without Negative Sampling for Recommendation.The 44th AAAI Conference on Artificial Intelligence.(AAAI 2020).
Chong Chen, Min Zhang, Weizhi Ma, Yiqun Liu and Shaoping Ma.Efficient Non-Sampling Factorization Machines for Optimal Context-Aware Recommendation.The Web Conference 2020(WWW 2020)
方法论
正常的隐性反馈(implicit feedback)推荐系统场景下,正例和负例(即未交互物品)比例失常(因为用户只能交互有限的几个物品)造成的数据稀疏性问题成为一个棘手难题。
要解决这个问题,要不就是用所有的负例数据不进行采样,但这样内存吃不消,计算开销也吃不消;要不就是用负采样(损失函数或者logloss做二分类,或者BPR做排序),但这样造成了性能损失以及模型表现的不稳定性。
本文为了解决这个问题,损失函数使用均方误差(对于分类问题来说可能还不太合适,个人感觉),用户与物品之间的交互使用线性方式,通过这种方式就能够将非采样推荐问题进行拆解,得到性能提高同时时间降低的推荐模型。
具体来说,用户与物品的交互使用 element-wise product 如下:
ϕ ( p u , q v ) = p u ⊙ q v (1) \phi \left(\mathbf{p}_{u}, \mathbf{q}_{v}\right) = \mathbf{p}_{u} \odot \mathbf{q}_{v} \tag{1} ϕ(pu,qv)=pu⊙qv(1)
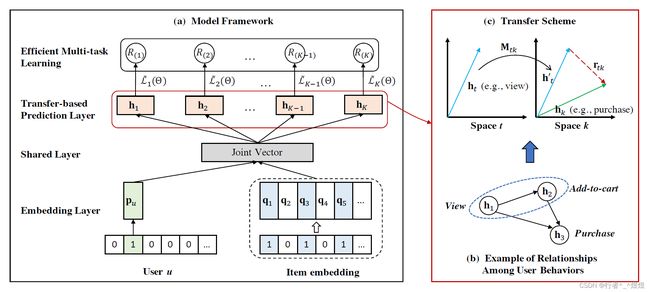
对应到具体预测层,使用 h k \mathbf{h}_{k} hk 表示预测层向量,有如下过程:
R ^ ( k ) u v = h k ⊤ ( p u ⊙ q v ) = ∑ i = 1 d h k , i p u , i q v , i (2) \hat{R}_{(k) u v}=\mathbf{h}_{k}^{\top}\left(\mathbf{p}_{u} \odot \mathbf{q}_{v}\right)=\sum_{i=1}^{d} h_{k, i} p_{u, i} q_{v, i} \tag{2} R^(k)uv=hk⊤(pu⊙qv)=i=1∑dhk,ipu,iqv,i(2)
则可以得到损失函数如下:
L k ( Θ ) = ∑ u ∈ B ∑ v ∈ V c u v k ( R ( k ) u v − R ^ ( k ) u v ) 2 = ∑ u ∈ B ∑ v ∈ V c u v k ( R ( k ) u v 2 − 2 R ( k ) u v R ^ ( k ) u v + R ^ ( k ) u v 2 ) (3) \begin{aligned} \mathcal{L}_{k}(\Theta) &=\sum_{u \in \mathbf{B}} \sum_{v \in \mathbf{V}} c_{u v}^{k}\left(R_{(k) u v}-\hat{R}_{(k) u v}\right)^{2} \\ &=\sum_{u \in \mathbf{B}} \sum_{v \in \mathbf{V}} c_{u v}^{k}\left(R_{(k) u v}^{2}-2 R_{(k) u v} \hat{R}_{(k) u v}+\hat{R}_{(k) u v}^{2}\right) \end{aligned} \tag{3} Lk(Θ)=u∈B∑v∈V∑cuvk(R(k)uv−R^(k)uv)2=u∈B∑v∈V∑cuvk(R(k)uv2−2R(k)uvR^(k)uv+R^(k)uv2)(3)
去掉常数项不影响梯度求导,另外将正例、负例分开运算,可以得到如下(推导可以参考 浅谈个性化推荐系统中的非采样学习 ):
L k ~ ( Θ ) = − 2 ∑ u ∈ B ∑ v ∈ V k + c u v k + R ( k ) u v R ^ ( k ) u v + ∑ u ∈ B ∑ v ∈ V c u v k R ^ ( k ) u v 2 = ∑ u ∈ B ∑ v ∈ V k + ( ( c u v k + − c u v k − ) R ^ ( k ) u v 2 − 2 c u v k + R ( k ) u v R ^ ( k ) u v ) ⏞ L k P ( Θ ) + ∑ u ∈ B ∑ v ∈ V c u v k − R ^ ( k ) u v 2 ⏞ L k A ( Θ ) = L k P ( Θ ) + ∑ i = 1 d ∑ j = 1 d ( ( h k , i h k , j ) ( ∑ u ∈ B p u , i p u , j ) ( ∑ v ∈ V c v k − q v , i q v , j ) ) (4) \begin{aligned} \tilde{\mathcal{L}_{k}}(\Theta) &=-2 \sum_{u \in \mathbf{B}} \sum_{v \in \mathbf{V}^{k+}} c_{u v}^{k+} R_{(k) u v} \hat{R}_{(k) u v}+\sum_{u \in \mathbf{B}} \sum_{v \in \mathbf{V}} c_{u v}^{k} \hat{R}_{(k) u v}^{2} \\ &=\overbrace{\sum_{u \in \mathbf{B}} \sum_{v \in \mathbf{V}^{k+}}\left(\left(c_{u v}^{k+}-c_{u v}^{k-}\right) \hat{R}_{(k) u v}^{2}-2 c_{u v}^{k+} R_{(k) u v} \hat{R}_{(k) u v}\right)}^{\mathcal{L}_{k}^{P}(\Theta)} +\overbrace{\sum_{u \in \mathbf{B}} \sum_{v \in \mathbf{V}} c_{u v}^{k-} \hat{R}_{(k) u v}^{2}}^{\mathcal{L}_{k}^{A}(\Theta)} \\ &= \mathcal{L}_{k}^{P}(\Theta) + \sum_{i=1}^{d} \sum_{j=1}^{d}\left(\left(h_{k, i} h_{k, j}\right)\left(\sum_{u \in \mathbf{B}} p_{u, i} p_{u, j}\right)\left(\sum_{v \in \mathbf{V}} c_{v}^{k-} q_{v, i} q_{v, j}\right)\right) \end{aligned} \tag{4} Lk~(Θ)=−2u∈B∑v∈Vk+∑cuvk+R(k)uvR^(k)uv+u∈B∑v∈V∑cuvkR^(k)uv2=u∈B∑v∈Vk+∑((cuvk+−cuvk−)R^(k)uv2−2cuvk+R(k)uvR^(k)uv) LkP(Θ)+u∈B∑v∈V∑cuvk−R^(k)uv2 LkA(Θ)=LkP(Θ)+i=1∑dj=1∑d((hk,ihk,j)(u∈B∑pu,ipu,j)(v∈V∑cvk−qv,iqv,j))(4)
总结
虽然文中提到的非采样方法普适性不是特别充分(即浅层非线性网络结构下的非采样),但是作者提供了一个比较好的思路,也切实解决了棘手的问题,具有相当的创新性。