cs224w 图神经网络 学习笔记（十一）Link Analysis: PageRank
课程链接：CS224W: Machine Learning with Graphs
课程视频：【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)
目录
-
- 1. Web as a Graph
- 2. How to organize the Web? ——PageRank
-
- 2.1 Links as Votes
- 2.2 The Flow Model
- 2.3 Random Walk Interpretation
- 2.4 PageRank equation
- 2.5 Computing PageRank
- 2.6 完整算法
- 3.Random Walk with Restarts and Personalized PageRank——PageRank在页面推荐中的应用
1. Web as a Graph
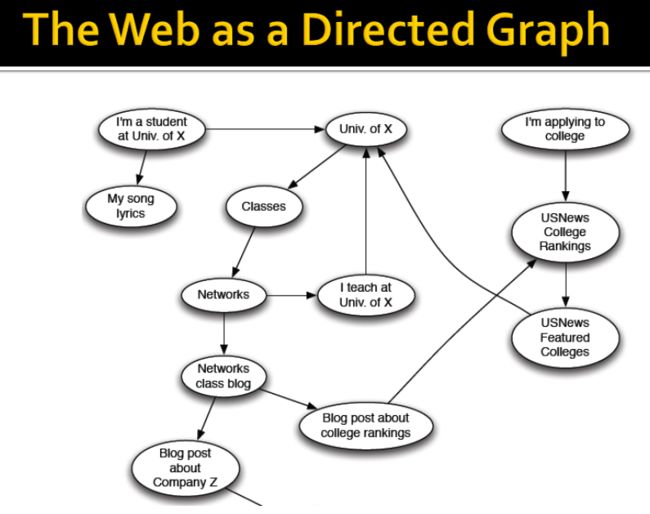
Web（互联网）实质上可以看成是一张有向图（Directed graph），节点是各种网页，边是网页之间的超链接。
对于这样的有向图，我们考虑两个问题：
- 给定节点 v v v，哪些节点可以到达 v v v？
- 从节点 v v v出发，可以到达哪些节点？
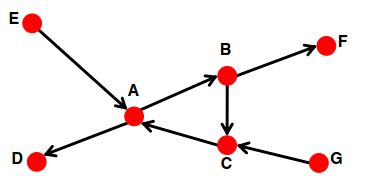
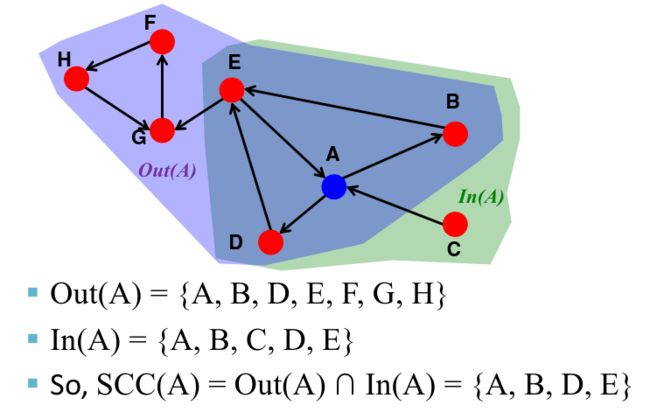
对于第一点，我们用集合 I n ( v ) = { w ∣ w can reach v } In(v)=\{w| w \text{ can reach }v\} In(v)={w∣w can reach v}来表示，比如下面这张图， I n ( A ) = { A , B , C , E , G } In(A)=\{A,B,C,E,G\} In(A)={A,B,C,E,G}。对于第二点，我们用集合 O u t ( v ) = { w ∣ v can reach w } Out(v)=\{w|v \text{ can reach } w\} Out(v)={w∣v can reach w}来表示，即 O u t ( A ) = { A , B , C , D , F } Out(A)=\{A,B,C,D,F\} Out(A)={A,B,C,D,F}。
任何有向图（Web）都可以通过下面这两种类型来表示：
| 类型 | 样式 | 描述 |
|---|---|---|
| Strongly connected 强连接图 |  |
任意节点之间都可以通过有向路径到达，即 I n ( A ) = O u t ( A ) = { A , B , C , D , E } In(A)=Out(A)=\{A,B,C,D,E\} In(A)=Out(A)={A,B,C,D,E}。 |
| Directed Acyclic Graph (DAG) 有向无环图 |  |
图中没有环路，节点 u u u可以到达节点 v v v，但是节点 v v v不能到达节点 u u u。 |
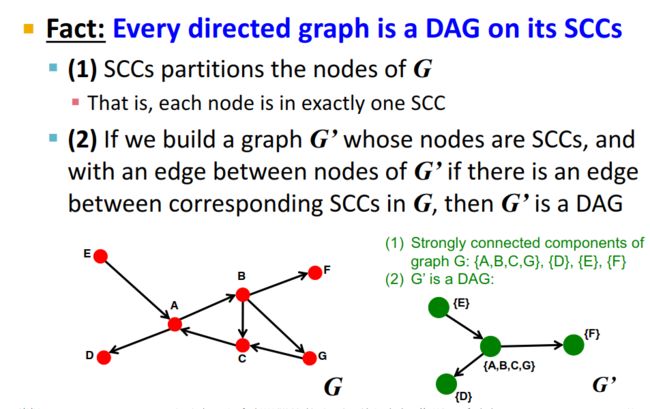
这样，我们可以关注一下复杂网络中的强连通分量（Strongly Connected Component，SCC）。SCC实际上是点的集合 S S S，在集合 S S S中任意两个点之间都有路径可以到达，并保证其他的SCC集合不包含这个集合 S S S。
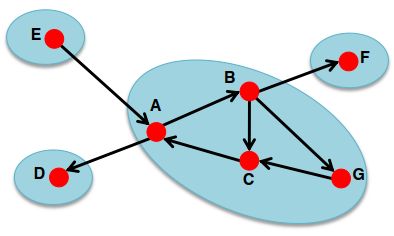
比如上面这张图的SCC包括：{A,B,C,G}, {D}, {E}, {F}。
任何一个有向图都是它强连通分量上的有向无环图。 下面是证明——
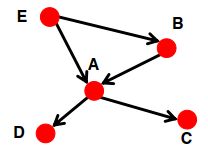
那么我们怎样找到节点 v v v的强连通分量呢？通过定义我们知道， I n ( v ) In(v) In(v)是所有能到达节点 v v v的节点集合， O u t ( v ) Out(v) Out(v)是所有节点 v v v能到达的节点集合，那么，节点 v v v的强连通分量就是 O u t ( v ) ⋂ I n ( v ) = O u t ( v , G ) ⋂ O u t ( v , G ′ ) Out(v) \bigcap In(v)=Out(v,G) \bigcap Out(v,G') Out(v)⋂In(v)=Out(v,G)⋂Out(v,G′)，其中 G ′ G' G′是 G G G的边的反转。我们可以使用图的深度优先搜索（DFS）/广度优先搜索（BFS）得到 O u t ( v , G ) Out(v,G) Out(v,G)和 O u t ( v , G ′ ) Out(v,G') Out(v,G′)。
采用BFS算法来计算 I n ( v ) In(v) In(v)和 O u t ( v ) Out(v) Out(v)，访问到的节点数量两极分化比较明显。（The BFS either visits many nodes or very few）
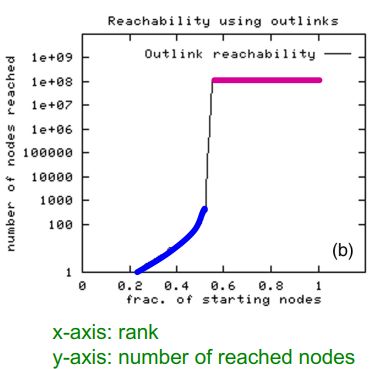
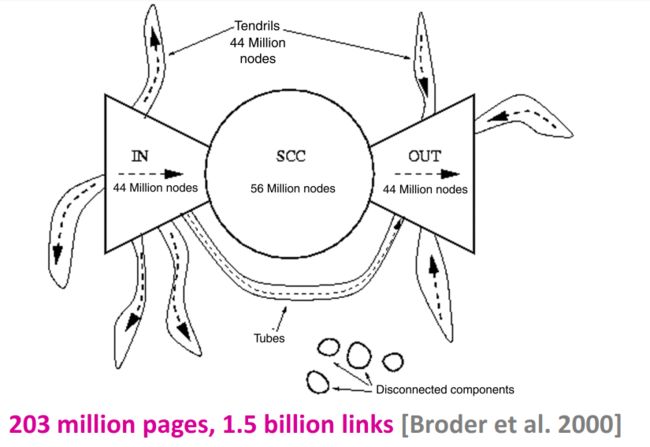
通过实验发现，在Web的网络上，对于随机的一个节点 v v v来说， O u t ( v ) ≈ 100 million (50% nodes) Out(v) \approx 100 \text{ million (50\% nodes)} Out(v)≈100 million (50% nodes)，且 I n ( v ) ≈ 100 million (50% nodes) In(v) \approx 100 \text{ million (50\% nodes)} In(v)≈100 million (50% nodes)；其极大强连通分量包括56 million个节点，大约是全部节点的28%。
这样一来，可以将Web的计算图表示成如下形式：
2. How to organize the Web? ——PageRank
PageRank的出发点在于：网络中的节点并不是同等重要的）。我们将介绍以下链接分析方法来计算图中节点的重要性:
- PageRank
- Personalized PageRank
- Random Walk with Restarts
2.1 Links as Votes
很明显，节点的重要性可以通过它的链接来体现——Page is more important if it has more links。当然，这些链接可以从In-coming links和Out-going links两个方面来体现。同时，节点外链的重要性也能体现其自身的重要性，Links from important pages count more——这是一个递归问题。
2.2 The Flow Model
总的来说：A “vote” from an important page is worth more.
每个节点的重要性会平均传给它的外链节点。设节点 i i i的重要程度为 r i r_i ri，有 d i d_i di个外链节点（out-links），则它传给这些节点的重要程度为 r i d i \frac {r_i}{d_i} diri。比如图中节点 j j j的重要程度 r j = r i 3 + r k 4 r_j=\frac{r_i}{3}+\frac{r_k}{4} rj=3ri+4rk。
也就是说，A page is important if it is pointed to by other important pages。同时，我们可以定义节点 j j j的排名（rank）：
r j = ∑ i → j r i d i r_j=\sum_{i \to j} \frac{r_i}{d_i} rj=i→j∑diri
其中 d i d_i di是节点 i i i的出度（out degree）。
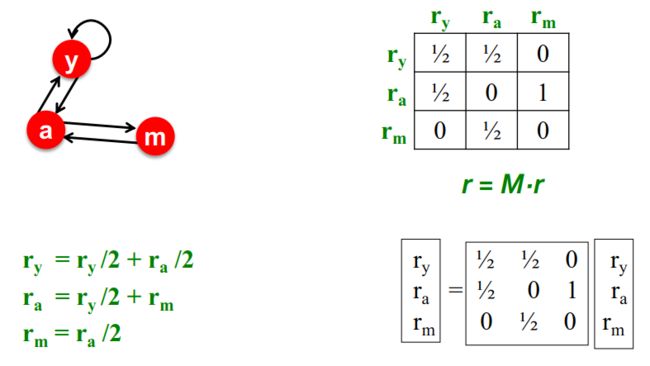
我们举一个例子：
我们可以得到flow equation:
r y = r y 2 + r a 2 r a = r y 2 + r m r m = r a 2 \begin{aligned} r_y &=\frac{r_y}{2}+\frac{r_a}{2} \\ r_a &=\frac{r_y}{2}+r_m \\ r_m &=\frac{r_a}{2} \\ \end{aligned} ryrarm=2ry+2ra=2ry+rm=2ra
这里是三个未知数，三个方程，可以求解得到相关的参数。
我们可以将上述flow equation写成矩阵形式：
r = M ⋅ r , r j = ∑ i → j r i d i r=M \cdot r, \text{ } r_j=\sum_{i \to j} \frac{r_i}{d_i} r=M⋅r, rj=i→j∑diri
其中 M M M是列随机矩阵（column stochastic matrix）。设节点 j j j的出度为 d j d_j dj，如果 j → i j \to i j→i，那么 M i j = 1 d j M_{ij}=\frac{1}{d_j} Mij=dj1，也就是说，矩阵 M M M的列和为1。
r i r_i ri是网页 i i i的重要度分数， ∑ i r i = 1 \sum_i r_i=1 ∑iri=1。
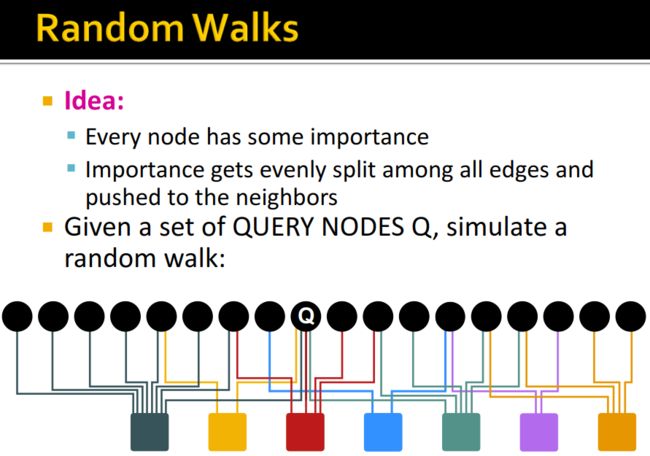
2.3 Random Walk Interpretation
假设有一个人在浏览网页，在时间 t t t时，他在浏览网页 i i i；在时间 t + 1 t+1 t+1时，这个人会随机地选取网页 i i i的外链 j j j进行访问；接着在网上冲浪时，上述过程会不断重复。
那么，设向量 p ( t ) p(t) p(t)表示状态概率， p ( t ) i p(t)_i p(t)i表示在时间 t t t位于网页 i i i的概率；也就是说， p ( t ) p(t) p(t)是基于网页的概率分布（a probability distribution over pages）。
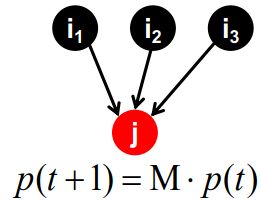
那么，在时间 t + 1 t+1 t+1时， p ( t + 1 ) = M ⋅ p ( t ) p(t+1)=M \cdot p(t) p(t+1)=M⋅p(t)。如果 p ( t + 1 ) = M ⋅ p ( t ) = p ( t ) p(t+1)=M \cdot p(t)=p(t) p(t+1)=M⋅p(t)=p(t)，那么称 p ( t ) p(t) p(t)为random walk的一个平稳分布（stationary distribution of a random walk）。
因为flow equation写成矩阵形式 r = M ⋅ r r=M \cdot r r=M⋅r，所以 r r r是矩阵 M M M的特征向量。我们可以采用**幂迭代（Power iteration）**的方法来求解 r r r。
幂迭代（Power iteration）
假设有一个带有 N N N个节点的web图，其中节点是页面，边是超链接。幂迭代是一种简单的求解 r r r迭代方案，可以为每个节点分配一个初始 r r r值，重复以下步骤直至收敛（ ∑ i ∣ r ( t + 1 ) − r t ∣ 1 < ε \sum_i |r^{(t+1)-r^{t}}|_1<\varepsilon ∑i∣r(t+1)−rt∣1<ε）。
- 初始化—— r ( 0 ) = [ 1 N , ⋯ , 1 N ] T r^{(0)}=[\frac{1}{N},\cdots,\frac{1}{N}]^T r(0)=[N1,⋯,N1]T。
- 迭代—— r ( t + 1 ) = M ⋅ r ( t ) r^{(t+1)}=M \cdot r^{(t)} r(t+1)=M⋅r(t)， r j ( t + 1 ) = ∑ i → j r i ( t ) d i r_j^{(t+1)}=\sum_{i \to j}\frac{r_i^{(t)}}{d_i} rj(t+1)=∑i→jdiri(t)。
- 迭代终止条件—— ∣ r ( t + 1 ) − r t ∣ 1 < ε |r^{(t+1)-r^{t}}|_1<\varepsilon ∣r(t+1)−rt∣1<ε。
但是，这个算法一定能收敛么？其收敛结果符合我们的预期么？收敛结果合理吗？
实际上，这个算法存在两个问题：
（1） Some pages are dead ends——有些页面是没有对外的链接的。
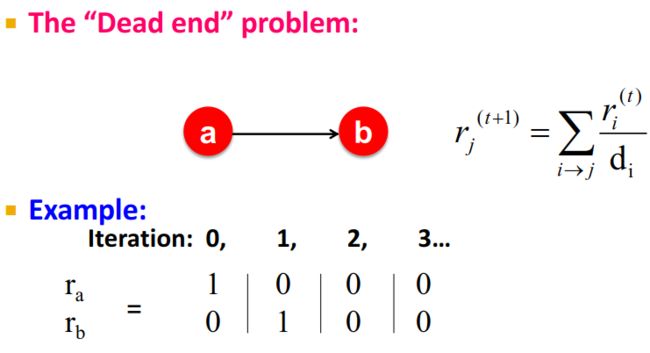
解决方法：
（2）Spider traps——(all out-links are within the group)。
Spider traps的解决方法：
2.4 PageRank equation
因此，我们可以得到PageRank方程——
r j = ∑ i → j β r i d i + ( 1 − β ) 1 N r_j=\sum_{i \to j} \beta \frac{r_i}{d_i}+(1-\beta) \frac{1}{N} rj=i→j∑βdiri+(1−β)N1
写成矩阵形式：
r = A ⋅ r r=A \cdot r r=A⋅r
其中 A A A为Google Matrix， A = β M + ( 1 − β ) [ 1 N ] N × N A=\beta M+(1-\beta)[\frac{1}{N}]_{N \times N} A=βM+(1−β)[N1]N×N。这里 β \beta β通常取0.8,0.9。
下面是一个例子：
2.5 Computing PageRank
PageRank的计算过程主要就是矩阵乘法 r n e w = A ⋅ r o l d r^{new}=A \cdot r^{old} rnew=A⋅rold。但有一个问题，当节点数量很大时，需要耗费很大的内存。
我们可以将PageRank方程的形式重新组织一下：
r = β M ⋅ r + [ 1 − β N ] N r=\beta M \cdot r+[\frac{1-\beta}{N}]_N r=βM⋅r+[N1−β]N
这里，矩阵 M M M是一个稀疏矩阵，而 [ 1 − β N ] N [\frac{1-\beta}{N}]_N [N1−β]N是一个稠密矩阵。因此，为了方便计算，每一轮迭代时我们都计算 r n e w = β M ⋅ r o l d r^{new}=\beta M \cdot r^{old} rnew=βM⋅rold，然后在 r n e w r^{new} rnew的基础上就上一个常数值 ( 1 − β ) / N (1-\beta)/N (1−β)/N。
2.6 完整算法
3.Random Walk with Restarts and Personalized PageRank——PageRank在页面推荐中的应用
