【深度学习MVS系列论文】P-MVSNet: Learning Patch-wise Matching Confidence Aggregation for Multi-View Stereo
P-MVSNet: Learning Patch-wise Matching Confidence Aggregation for Multi-View Stereo ICCV 2019
Abstract
volume在深度和空间方向应该都是各向异性的,但之前都是各向同性的处理问题
本文基于各向同性和各向异性的3D卷积构建网络
两大核心模块:
-
patch-wise aggregation module: 从提取的特征中聚集像素级别的相关信息 → matching confidence volume
提高匹配准确度和鲁棒性
-
hybrid 3D U-Net: 预测深度假设分布和深度图
Motivation
【问题一】
MVS核心步骤是构建pixel-wise matching cost volume
核心思想是首先在参考图像上通过平面扫描构建plane-sweep volume,然后在每个深度采样间隔计算ref和src的匹配代价
主流方法都是计算方差,但这样所有点对对匹配代价的贡献都是一样的(@doubleZ 在读MVSNet就注意过的问题)
当特征很相似但不匹配的时候,会有一个比较小的matching cost,但这仍然会导致后续深度图的错误估计
解决方案:highlight the importance of pixels in reference image during calculation of the matching confidence volume
【问题二】
现有方法构建完cost volume后直接进行正则化,对noisy data不鲁棒
而且volume本质上是各向异性的:我们只能从深度方向估计深度图,其他方向没有这个信息
【解决方案】
-
根据MSE构建pixel-wise matching confidence volume(给ref图更多的偏好)
-
patch-wise confidence aggregation方法聚合刚刚像素级别的匹配代价体(pixel-wise → patch-wise)
-
hybrid 3D U-Net with 各向同性和各向异性的3D卷积,充分利用volume的上下文信息,构建probability volume
- 高分辨率级别有一个特殊的refinement结构
-
点云重建时有一些filter和fusion的方法
- depth-confidence, depth-consistency 标准
Related Work
写这部分可以从这三部分入手,不过确实都是老生常谈的了
【Conventional MVS】
- patch based: 首先根据纹理丰富区域构建surface的patch重建,再逐步传播到弱纹理区域
- deformable polygonal mesh based:首先估计surface,再迭代优化
- voxel based: 划分空间网格,让点附着在表面
- ✨depth map based
【Learning-based stereo】
精准校正的图像对很难
【Learning-based MVS】
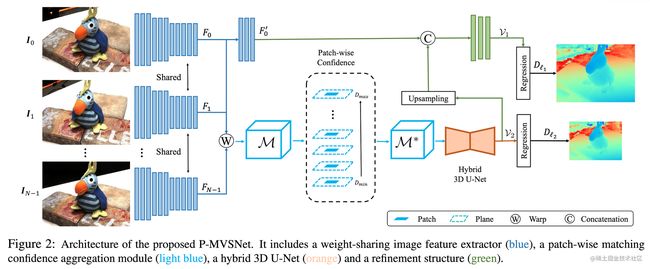
Architecture
四个大部分,个人感觉跟MVSNet没有本质区别:
- 共享权重的image feature extractor
- patch-wise matching confidence aggregation module
- hybrid 3D U-Net based depth map inference network
- refinement structure
图像特征提取
encoder-decoder architecture(感觉是硬凑名字,根本只是两阶段不同的卷积)
- encoder: 对于所有图像做,得到l2级别的特征图Fi,用于构建Matching Confidence Volume(MCV)
- decoder: 只对ref图做,得到l1级别的特征图F0’,它用于指导更高分辨率深度图的估计
输出的Channel都变为16维,l2尺寸缩小1/4,l1尺寸缩小1/2
图像块级别匹配置信度
对l2特征图首先根据平面扫描构建MCV特征体,然后通过网络将pixel-wise MCV转换为patch-wise MCV(增加鲁棒性和准确度)
【pixel-wise MCV】
跟MVSNet压根就是一样的
M ( d , p , c ) \mathcal{M}(d, \boldsymbol{p}, c) M(d,p,c)的维度是 Z × H 4 × W 4 × C Z \times \frac{H}{4} \times \frac{W}{4} \times C Z×4H×4W×C,计算方法也就是投影和方差
M ( d , p , c ) = exp ( − ∑ j = 1 N − 1 ( F j ( p ′ , c ) − F 0 ( p , c ) ) 2 N − 1 ) \mathcal{M}(d, \boldsymbol{p}, c)=\exp \left(-\frac{\sum_{j=1}^{N-1}\left(F_{j}\left(\boldsymbol{p}^{\prime}, c\right)-F_{0}(\boldsymbol{p}, c)\right)^{2}}{N-1}\right) M(d,p,c)=exp(−N−1∑j=1N−1(Fj(p′,c)−F0(p,c))2)
p’是相邻特征图Fj中p的对应点;Fj(p’, c)通过差值计算(实际上跟MVSNet一样,只是用公式表达出来了)
接下来对于每个深度假设平面 π d \pi_d πd进行patch-wise的聚合
M ⋆ ( d , p , c ) = tanh ( ρ 3 ( Ω 2 ( M a ( d , p , c ) ) ) ) M a ( d , p , c ) = ρ 1 ( M ( d , p , c ) ) + ρ 2 ( Ω 1 ( M ( d , p , c ) ) ) \begin{aligned}\mathcal{M}^{\star}(d, \boldsymbol{p}, c) &=\tanh \left(\rho_{3}\left(\Omega_{2}\left(\mathcal{M}^{a}(d, \boldsymbol{p}, c)\right)\right)\right) \\\mathcal{M}^{a}(d, \boldsymbol{p}, c) &=\rho_{1}(\mathcal{M}(d, \boldsymbol{p}, c))+\rho_{2}\left(\Omega_{1}(\mathcal{M}(d, \boldsymbol{p}, c))\right)\end{aligned} M⋆(d,p,c)Ma(d,p,c)=tanh(ρ3(Ω2(Ma(d,p,c))))=ρ1(M(d,p,c))+ρ2(Ω1(M(d,p,c)))
-
Ω 1 ( ⋅ ) \Omega_1(\cdot) Ω1(⋅):假设平面上以p为中心的3*3patch w 1 w_1 w1
-
Ω 2 ( ⋅ ) \Omega_2(\cdot) Ω2(⋅):沿深度方向以p为中心的三个相邻patch的结合
-
ρ 1 , ρ 2 , ρ 3 \rho_1, \rho_2, \rho_3 ρ1,ρ2,ρ3:learnable functions that take into account the multi-channel feature matching confidence
- ρ 1 \rho_1 ρ1: 1 × 1 × 1 1\times1\times1 1×1×1 3D卷积+BN+ReLU,只关注p这一点的多通道匹配置信度聚合
- ρ 2 \rho_2 ρ2: 3 × 3 × 3 3\times3\times3 3×3×3 3D卷积+BN+ReLU,在相邻像素区域 w 1 w_1 w1融合匹配信息
- ρ 3 \rho_3 ρ3: 3 × 3 × 3 3\times3\times3 3×3×3 3D卷积+BN,在多patch中聚合matching confidence
-
t a n h ( ⋅ ) tanh(\cdot) tanh(⋅): 激活函数
通过学习式的方法聚合代价体而不是启发式的方法
最终每个像素在每个深度假设的cost不再是一个scalar,而是一个vector
提升匹配的鲁棒性和准确度
深度图估计
M ∗ \mathcal{M^*} M∗接下来通过hybrid 3D U-Net,计算得到latent probability volume(LPV),表示ref图里每个像素在深度方向的潜在概率分布,此时已经把特征维度干掉了,维度变为[Z, H/4, W/4]
3D U-Net由一系列各向同性(卷积各方向维度相同)和各向异性的3D卷积层组成:
-
浅层:两种各向异性的卷积
- 133: 在每个假设平面聚集信息
- 711: 在深度方向扩大感受野,获取全局信息
-
深层:各向同性的卷积
- 333: fuse more context information
之后进行depth regression估计深度图,具体方法还是 ∑ d × P ( d ) \sum d \times P(d) ∑d×P(d)
得到的深度图分辨率一般比较低,再通过之前l1级别的特征图指导refinement得到一张更高分辨率的深度图
点云重建
不同深度图可能由于存在错误深度而无法匹配(不同深度图估计同一点的深度不一样)
两种filter策略丢弃错误估计的点:
【depth-confidence】
去掉明显不可靠的预测
最好的情况肯定是每个点的深度维度概率是单峰
方法是通过概率体在深度维度构建confidence map,而且利用了之前的两种分辨率的信息,最终在l1级别的confidence map上滤除置信度小于0.5的点
【depth-consistency】
放弃相邻图像间不一致的深度
方法还是按p的预测深度d§把它投影到另一张图的p’上,再按照d(p’)投会来,如果误差小则认为满足一致性,至少要做到ref跟两张src的一致性才通过测试
创新点在于:对于有相机参数真值的点采用双线性插值方法,否则采用depth-consistency first策略,Fig 5略
Experiment
采用SWATS自动从Adam切换为SGD以获得更好的泛化能力
Future Work
- 更高精度数据集
- 内存消耗和计算复杂度
- 融合语义信息