论文精读《OFT: Orthographic Feature Transform for Monocular 3D Object Detection》
OFT: Orthographic Feature Transform for Monocular 3D Object Detection
文章目录
- OFT: Orthographic Feature Transform for Monocular 3D Object Detection
- 论文精读
-
- 摘要(Abstract)
- 1. 介绍(Introduction)
- 2. 相关工作(Related Work)
- 3. 3D目标检测架构(3D Object Detection Architecture)
-
- 3.1 特征提取(Feature extraction)
- 3.2 正交特征变换(Orthographic feature transform)
- 3.3 自上而下的网络(Topdown network)
- 3.4 置信度预测(Confidence map prediction)
- 3.5 位置和检测框的预测(Localization and bounding box estimation)
- 3.5 非极大值抑制(Nonmaximum suppression)
- 参考
论文精读
摘要(Abstract)
研究现状
从单目图像中进行3D目标检测已被证明是一项极具挑战性的任务,其系统性能甚至还达不到基于雷达对应系统性能的10%。对这种性能差距的一种解释是,现有的系统完全处于由于基于透视图像的表示,物体的外观和规模随着深度和距离的变化而急剧变化,因此很难推断。
本文工作:OFT
在这项工作中,我们认为推理三维世界的能力是三维物体检测任务的一个基本元素。为此,我们引入正交法特征变换(orthographic feature transform),它使我们能够通过将基于图像的特征映射到正交3D空间,实现了对图像域的转义。这让我们能够在尺度一致且物体之间的距离有意义的领域中全面地推理场景的空间配置。我们将这种转换应用于端到端深度学习架构,并在KITTI 3D对象基准测试上实现了最先进的性能。
1. 介绍(Introduction)
任何自治代理的成功都取决于它在周围环境中检测和定位对象的能力。预测、回避和路径规划都依赖于对场景中其他实体的3D位置和尺寸的稳健估计。这使得三维边界盒检测成为计算机视觉和机器人技术的一个重要问题,特别是在自动驾驶的背景下。迄今为止,三维目标检测的文献主要是利用丰富的激光雷达点云的方法,而纯图像方法由于缺乏激光雷达的绝对深度信息,其性能明显落后。
考虑到现有激光雷达设备的高成本,激光雷达点云在远距离的稀疏性,以及传感器冗余的需求,从单眼图像中精确地检测三维目标仍然是一个重要的研究目标。为此,我们提出了一种新颖的3D目标检测算法,该算法以单眼RGB图像作为输入,生成高质量的3D检测框,在具有挑战性的KITTI基准测试中实现了单目方法中最先进的性能。
在很多意义上,图像是一种极具挑战性的方式。透视投影意味着一个物体的尺度随着距离相机的远近变化很大;它的外观可以根据视点的不同而发生巨大的变化;3D世界中的距离无法直接推断。这些因素给单眼三维目标检测系统带来了巨大的挑战。
一种更为无害的表示是许多基于雷达的方法中普遍使用的正交法鸟瞰图。在这种表示下,尺度是同质的;外观在很大程度上与视角无关;物体之间的距离是有意义的。因此,我们的关键见解是,尽可能多的推理应该在这个正交法空间中执行,而不是直接在基于像素的图像域上执行。这一见解被证明对我们所提议的系统的成功至关重要。
然而,目前还不清楚如何仅从单眼图像构建这样的表示。因此,我们引入正交特征变换(OFT):一个可微函数,将从透视RGB图像中提取的一组特征映射到正交鸟瞰特征图的一种变换。关键是,我们不依赖任何明确的深度概念:相反,我们的系统建立了一个内部表示,能够确定图像中的哪些特征与鸟瞰视图中的每个位置相关。我们应用了一种深度卷积神经网络,即自顶向下网络,来对场景的三维构型进行局部推理。
我们工作的主要贡献如下:
- 引入基于透视图像的特征映射为鸟瞰图视角的正交特征变换,并使用积分图像对平均池化进行高效处理。
- 构建了DL结构用于预测单目RGB图像目标的3D框;
- 强调3D推理在目标检测任务中的重要性;
2. 相关工作(Related Work)
2D object detection
主要可分为 single stage detectors:YOLO、SSD、RetinaNet等;two-stage detectors:Faster R-CNN、 FPN 等;到目前为止,绝大多数的3D目标检测方法都采用了后一种方法,部分原因是三维空间中固定大小区域到图像空间中可变大小区域的映射比较困难。作者通过OFT转换克服了这一限制,允许我们利用one-stage结构的速度和精度优势。
3D object detection from LiDAR
3D目标检测对自动驾驶具有重要意义,已经有很多基于LiDAR的方法都取得了较大成功。大多数变化来自激光雷达点云的编码方式。
3D object detection from images
由于缺乏绝对深度信息,从图像中获取3D边界框是个具有挑战性的问题。许多方法都是从使用上述标准的检测器中提取的2D框开始,在此基础上,它们要么直接对每个区域回归出3D姿态参数,要么将3D模板匹配到图像**;**以上所有工作的一个主要限制是,每个区域的proposal或者bbox都是独立处理的,排除了任何关于场景3D配置的联合推理。我们的方法类似于的特征聚合步骤,但是对生成的proposal应用了一个二级卷积网络,同时保留了它们的空间配置。
Integral images
自从Viola和Jones开创性的工作中引入积分图像以来,积分图像(Integral image)就从根本上与目标检测相关联。它们在包括AVOD,MV3D,Mono3D,3DOP在内的许多现代3D目标检测方法中形成了重要的组成部分
3. 3D目标检测架构(3D Object Detection Architecture)
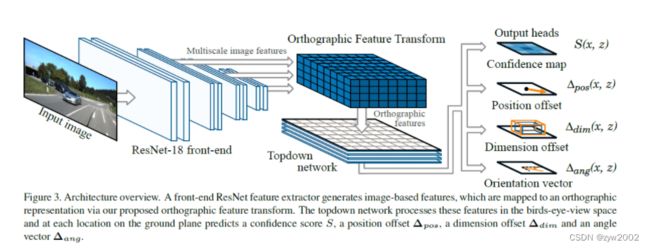
提出了一种通过投影提取正交特征的方式:将卷积网络对图像卷积得到的特征,经过3D到2D的投影和平均池化的操作取到3D鸟瞰图上,从而构成3D鸟瞰图的特征图。即可在该特征图上回归各种3D目标属性。
本节作者描述了单目图像中提取3D边界框的完整方法。算法主要由5个部分构成:
- 前端由Font-end ResNet 特征提取器来提取输入图像的多尺度特征图;
- orthographic feature transform 将每个尺度上基于图像的特征转换为鸟瞰图的正交表述法;
- 一种由一系列ResNet残差单元组成的A topdown network,它以不受图像中观察到的透视效果影响的方式来处理鸟瞰视角的特征图;
- 一组output heads,分别生成每个对象类和每个类别在地平面的位置,置信度得分,位置偏移量,尺度偏移量和方向向量;
- non-maximum suppression和decoding stage,该阶段识别出峰值,并生成离散边界框预测;
算法的整体架构图
3.1 特征提取(Feature extraction)
利用Resnet生成多级多尺度特征图,这些特征编码了图像中低层结构的信息,这些信息构成了自上而下网络的基本组件,以构建场景的隐式3D表示。前端网络还负责根据图像特征的大小推断深度信息,因为后续阶段的结构目标是消除尺度的变化。
3.2 正交特征变换(Orthographic feature transform)
Orthographic Feature Transform (OFT) 的目的是用来将基于图像的特征 f ( u , v ) f(u,v) f(u,v) 填充到基于体素的三维特征中。
(1) Image Feature→Voxel Feature
体素特征图是一个均匀分割的3D网格立方体(立方体大小是 W × H × D W\times H\times D W×H×D, 网格大小是 r r r),与地面保持恒定的距离 y 0 y_0 y0
对于每个voxel投影到Image上是一个六边形,把这个六边形近似成一个长方形(长方形的左上角和右下角的点坐标分别是 ( u 1 , v 1 ) (u_1,v_1) (u1,v1)和 ( u 2 , v 2 ) (u_2,v_2) (u2,v2) )
Image feature 和 Voxel Feature 的位置转换关系如下:
u 1 = f x − 0.5 r z + 0.5 x ∣ x ∣ r + c u , v 1 = f y − 0.5 r z + 0.5 y ∣ y ∣ r + c v u 2 = f x + 0.5 r z − 0.5 x ∣ x ∣ r + c u , v 2 = f y + 0.5 r z − 0.5 y ∣ y ∣ r + c v \begin{array}{ll}u_1=f \frac{x-0.5 r}{z+0.5 \frac{x}{|x|} r}+c_u, & v_1=f \frac{y-0.5 r}{z+0.5 \frac{y}{|y|} r}+c_v \\u_2=f \frac{x+0.5 r}{z-0.5 \frac{x}{|x|} r}+c_u, & v_2=f \frac{y+0.5 r}{z-0.5 \frac{y}{|y|} r}+c_v\end{array} u1=fz+0.5∣x∣xrx−0.5r+cu,u2=fz−0.5∣x∣xrx+0.5r+cu,v1=fz+0.5∣y∣yry−0.5r+cvv2=fz−0.5∣y∣yry+0.5r+cv
其中 f f f 是相机焦距, ( c u , c v ) (c_u,c_v) (cu,cv) 是基准点。
Voxel Feature 中Voxel特征是通过对Image Feature 中的对应的区域进行平均池化得到的。
(2) Voxel Feature → Orthographic Feature
将3D的Voxel Feature 折叠到 2D 的 Orthographic Feature 上。
沿着垂直方向,对带权的体素特征进行求和。其中这个权重 W ( y ) ∈ R n × n W(y) \in \mathbb{R}^{n \times n} W(y)∈Rn×n 是通过学习得到的。
h ( x , z ) = ∑ y = y 0 y 0 + H W ( y ) g ( x , y , z ) \begin{aligned} & \\ &\qquad \mathbf{h}(x, z)=\sum_{y=y_0}^{y_0+H} W(y) \mathbf{g}(x, y, z) \end{aligned} h(x,z)=y=y0∑y0+HW(y)g(x,y,z)
3.3 自上而下的网络(Topdown network)
3D推理组件由一个子网络构成,称之为自上而下网络。这是一个简单的卷积网络,使用ResNet风格的skip连接,它在之前描述的OFT阶段生成的2D特征图 h 上运行。距离相机较远和较近的特征图得到完全相同的处理,尽管对应的图像区域要小得多。
3.4 置信度预测(Confidence map prediction)
置信度图S(x,z)是个平滑函数,它表示在(x,y0,z)位置是否存在以该位置为中心带边界框的目标存在可能性。其中y0 表示在相机下方距离地面的距离。给定N个真实目标的真实边界框中心 p i = [ x i , y i , z i ] T , i = 1 , … , N p_i=\left[x_i, y_i, z_i\right]^T, \mathrm{i}=1, \ldots, \mathrm{N} pi=[xi,yi,zi]T,i=1,…,N
我们计算GT置信度图为一个平滑的高斯区域,其以目标中心为中心,宽度为
,在位置(x,z)置信度公式为:
S ( x , z ) = max i exp ( − ( x i − x ) 2 + ( z i − z ) 2 2 σ 2 ) S(x, z)=\max _i \exp \left(-\frac{\left(x_i-x\right)^2+\left(z_i-z\right)^2}{2 \sigma^2}\right) S(x,z)=imaxexp(−2σ2(xi−x)2+(zi−z)2)
网络置信度图预测分支头使用 L1 loss来训练的,回归到正交网格 H上每个位置的GT 置信度上。由于正样本(高置信度的位置)要远远少于负样本,为了克服该问题,作者引入常量因子0.01 ,将其乘以负样本位置(S(x,z)得分<0.05的位置)这样减少大量负样本的影响
3.5 位置和检测框的预测(Localization and bounding box estimation)
在对应的目标pi 的中心追加了一个额外的网络输出,输出头可以预测距离地面网格单元位置
( x , y 0 , z ) 的相对偏移 Δ pos \begin{gathered} \left(x, y_0, z\right) \text { 的相对偏移 } \\ \Delta \text { pos } \end{gathered} (x,y0,z) 的相对偏移 Δ pos
是尺寸输出,预测目标 i i i 的尺寸
d i = [ w i , h i , l i ] 和给定类别所有目标的平均尺寸 d ˉ = [ w ˉ , h ˉ , l ˉ ] 之间的对数尺度偏移 Δ dim : Δ dim ( x , z ) = [ log w i w ˉ , log h i h ˉ , log l i l ˉ ] T \begin{gathered} d_i=\left[w_i, h_i, l_i\right] \text { 和给定类别所有目标的平均尺寸 } \\ \bar{d}=[\bar{w}, \bar{h}, \bar{l}] \text { 之间的对数尺度偏移 } \\ \Delta \operatorname{dim}: \\ \Delta \operatorname{dim}(x, z)=\left[\log \frac{w_i}{\bar{w}}, \log \frac{h_i}{\bar{h}}, \log \frac{l_i}{\bar{l}}\right]^T \end{gathered} di=[wi,hi,li] 和给定类别所有目标的平均尺寸 dˉ=[wˉ,hˉ,lˉ] 之间的对数尺度偏移 Δdim:Δdim(x,z)=[logwˉwi,loghˉhi,loglˉli]T
方向输出分支头,预测目标绕y轴的方向角
θ i \theta_i θi 的sine和cosine值:
Δang ( x , z ) = [ sin θ i , cos θ i ] T \operatorname{\Delta ang}(x, z)=\left[\sin \theta_i, \cos \theta_i\right]^T Δang(x,z)=[sinθi,cosθi]T
位置偏移
Δ pos,尺寸偏移 Δ d i m ,方向向量 \begin{aligned} &\Delta \text { pos,尺寸偏移 } \\ &\Delta d i m \text { ,方向向量 } \end{aligned} Δ pos,尺寸偏移 Δdim ,方向向量
Δ a n g 都是 L1 lossi川练的。 \Delta a n g_{\text {都是 L1 lossi川练的。 }} Δang都是 L1 lossi川练的。
3.5 非极大值抑制(Nonmaximum suppression)
首先用高斯核 (其宽度为 σ N M S \sigma_{N M S} σNMS ) 来平滑置信度图。在平滑后的置信度图上位置 ( x i , z i ) 的值 \left(x_i, z_i\right)_{\text {的值 }} (xi,zi)的值
S ~ \tilde{S} S~ 被认为是最大的,如果它满足下式:
S ~ ( x i , z i ) ≥ S ~ ( x i + m , z i + n ) ∀ m , n ∈ − 1 , 0 , 1 \begin{gathered} \tilde{S}\left(x_i, z_i\right) \geq \tilde{S}\left(x_i+m, z_i+n\right) \\ \forall m, n \in-1,0,1 \end{gathered} S~(xi,zi)≥S~(xi+m,zi+n)∀m,n∈−1,0,1
在产生的峰值位置中,任何小于给定阈值 t \mathrm{t} t 的置信度
S ( x i , y i ) 都将被排除。 S\left(x_i, y_i\right)_{\text {都将被排除。 }} S(xi,yi)都将被排除。
参考
Orthographic Feature Transform for Monocular 3D Object Detection
https://github.com/tom-roddick/oft
OFT论文解读_思绪零乱成海的博客-CSDN博客
【论文翻译】Orthographic Feature Transform for Monocular 3D Object Detection_ciky奇的博客-CSDN博客