好多算法之类的,看理论描述,让人似懂非懂,代码走一走,现象就了然了。
引:
from sklearn import tree names = ['size', 'scale', 'fruit', 'butt'] labels = [1,1,1,1,1,0,0,0] p1 = [2,1,0,1] p2 = [1,1,0,1] p3 = [1,1,0,0] p4 = [1,1,0,0] n1 = [0,0,0,0] n2 = [1,0,0,0] n3 = [0,0,1,0] n4 = [1,1,0,0] data = [p1, p2, p3, p4, n1, n2, n3, n4] def pred(test): dtre = tree.DecisionTreeClassifier() dtre = dtre.fit(data, labels) print(dtre.predict([test])) with open('treeDemo.dot', 'w') as f: f = tree.export_graphviz(dtre, out_file = f, feature_names = names) pred([1,1,0,1])
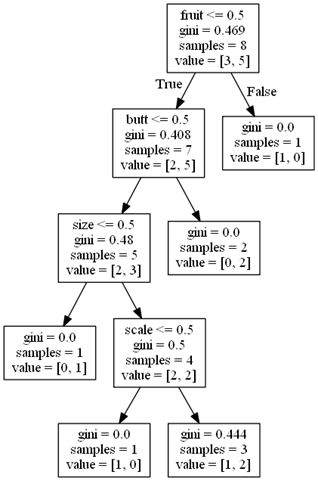
画出的树如下:
关于这个树是怎么来的,如果很粗暴地看列的数据浮动情况:
或者说是方差,方差最小该是第三列,fruit,然后是butt,scale(方差3.0),size(方差3.2857)。再一看树节点的分叉情况,fruit,butt,size,scale,两相比较,好像发现了什么?
衡量数据无序度:
划分数据集的大原则是:将无序的数据变得更加有序。
那么如何评价数据有序程度?比较直观地,可以直接看数据间的差距,差距越大,无序度越高。但这显然还不够聪明。组织无序数据的一种方法是使用信息论度量信息。在划分数据集之前之后信息发生的变化叫做信息增益(information gain),为了让信息更准确分类,必然希望信息增益最大化,那么信息增益如何计算?
集合信息的度量方式叫做香农熵(名字源自信息论支付克劳德·香农),简称熵(entropy)。
熵定义为期望值,如果P(Xi) 是分类为i的概率,那么对于分类i的熵L(Xi) 的公式是:
![]()
显然地,随着分类的概率越高,其熵(L(X))越小。这很有意思,概率越高的东西,大家的期望值越低;越容易发生的事情,大家对它的发生不惊奇,没有期待;反过来说,发生几率越小的事情,一旦发生了,大家都会很惊奇,那么这个叫惊奇度可能比较合适hhh。
计算熵值,不仅是要看单个分类的熵,要看所有分类的期望值,其中n是分类数目:
从这个公式看来,这是一个带权重(是i分类的概率)的期望和。这个值可以用来表示事情的无序度。熵越高,则混合的数据越多。
| 为什么是以2为底的对数? 首先还是可以从“数学期望”(设为E(X))是个什么东西入手,E(X) = ∑XP(X),这个X是个随机变量,可以把数学期望看成是:加权的概率和。那么如何确定随机变量X呢?可以这样看:X是这个概率出现的次数。我的描述可能有些不对,但从直观的加权上,大概是这样。例如有人去打猎,猎中1只概率1/5,猎中2只是3/5,猎中3只是1/5,那么他这一次出猎可能猎中多少只?E(X) = 1*1/5 + 2*3/5 + 3*1/5 = 2,每次平均2只。 现在再来琢磨log2,为什么随机变量是2的对数?——我们来猜数字,这个数字在1~32,猜16,如果比16大就猜8,比8大就猜(8, 16)之间,以此类推,最多5次可以猜出——所有可能情况与对数log有关。而如果已经能排除一些不可能数字,那猜到答案的速度会更快。
参考:https://blog.csdn.net/lingtianyulong/article/details/34522757 |
另一种度量集合无序度的方法是基尼不纯度(Gini impurity),公式原理并不太明白,先摆出来吧:
信息增益:
信息增益(设为infoGain)作为无序度减少程度。
某一列的直接按分类结果(label)的信息熵(设为baseEnt)与该列按标志值分类的信息熵(设为newEnt)的差距。
ID3算法应用其差值:
infoGain = baseEntropy – newEntropy
C4.5算法应用其比值,其中i为列标志值分类总数:
ID3创建决策树:
以信息熵来作为数据无序度判断依据的话,决策树如何创建?
下面以这个 DataSet 作为计算demo,列名分别是:“不浮出水面是否可以生存”,“是否有脚蹼”,特别地,最后一列为 “是否为鱼类” 的分类标签:
| no surfacing |
flippers |
Label |
| 1 |
1 |
yes |
| 1 |
1 |
yes |
| 1 |
0 |
no |
| 0 |
1 |
no |
| 0 |
1 |
no |
那么有矩阵:
[[1,1,’yes’],
[1,1,’yes’],
[ 1,0,’no’],
[ 0,1,’no’],
[ 0,1,’no’]]
步骤1:
以label列作为分类标准,计算第一列熵,首先看第一列和标签列,计算如下图:
[0] 此处直接以0和1作为数据划分判断,对于标志性的数据可行,但如果是数值型的数据,那么就需要采取另一种决策树的构造算法。
以此类推,计算第2列:
步骤2:
比较所有列的熵,取无序度最小(也即信息增益 infoGain = baseColEnt - newColEnt 最大)的列(特征),做为决策树的节点。
上例中,第一列信息熵最高,那么第一个节点就是no surfacing特征列。
步骤3:
处理分裂节点。
此时取步骤2中获得的特征列作DataSet行上的分类,划分出若干数据块后,其中信息熵为0的数据块是不再分裂的节点;信息熵不为0的,需要处理为新的DataSet,回到步骤1进行计算。
对于本例,按照第一列,可以把DataSet分裂成2个数据块[1]:
[[1,1,’yes’],
[1,1,’yes’],
[ 1,0,’no’]] ——设为DataSet_A
和:
[[ 0,1,’no’],
[ 0,1,’no’]] ——设为DataSet_B
[1] 这两个数据块的划分还是依靠标志型数据的0与1,数值型数据采用另外的决策树构造法。
此时DataSet_B全部为一个分类,那么这个节点就结束了。
DataSet_A的标签分类不止一个,那么这个节点还需要继续分裂,而此时DataSet_A的第一列曾经做过分类列,新的DataSet可以除去这一列,即DataSet = [[1,’yes’],[1,’yes’] ,[0,’no’]]重新进入步骤1。
步骤4:
绘制图像,叶节点为分类的标签结果,其中0为False,1为True。
这种构造决策树的方法叫做ID3,ID3无法直接处理数值型数据,尽管可以通过量化的方法将数值型数据转化为标志型的数据,但如果存在太多的特征划分,ID3算法仍会有其他问题。其他的决策树构造法,有C4.5和CART等。
ID3算法构建的决策树,其数据值需要是标志型(例如0表示否,1表示是,或者其他字符串[2],标志总数较少)的数据,如果是数值型的数据,需要换其他构建方法。另外,可能会出现匹配选项过多的问题,这叫做过度匹配(overfitting),为了减少过度匹配,可以裁剪决策树。
[2] 一个隐形眼镜类型的示例,数据集如下,列名依次为:age,prescript,astigmatic,tearRate,最后一列为标签列,其中no lenses表示不适合佩戴隐形眼镜,soft:软材质,hard:硬材质。
young myope no reduced no lenses
young myope no normal soft
young myope yes reduced no lenses
young myope yes normal hard
young hyper no reduced no lenses
young hyper no normal soft
young hyper yes reduced no lenses
young hyper yes normal hard
pre myope no reduced no lenses
pre myope no normal soft
pre myope yes reduced no lenses
pre myope yes normal hard
pre hyper no reduced no lenses
pre hyper no normal soft
pre hyper yes reduced no lenses
pre hyper yes normal no lenses
presbyopic myope no reduced no lenses
presbyopic myope no normal no lenses
presbyopic myope yes reduced no lenses
presbyopic myope yes normal hard
presbyopic hyper no reduced no lenses
presbyopic hyper no normal soft
presbyopic hyper yes reduced no lenses
presbyopic hyper yes normal no lenses
其决策树如下:
创建决策树的类库:
from sklearn import tree
具体代码可见上文,不过代码示例是以基尼不纯度作为数据划分的评判准则,可以在声明树对象的时候传入参数,criterion = “entropy”设置决策树以信息熵作为划分标准:
dtre = tree.DecisionTreeClassifier(criterion="entropy")
此外,
with open('treeDemo.dot', 'w') as f: f = tree.export_graphviz(dtre, out_file = f, feature_names = names)
这两句会创建保存在运行路径命名为treeDemo的dot文件,打开可见树节点信息:
digraph Tree {
node [shape=box] ;
0 [label="butt <= 0.5\nentropy = 0.954\nsamples = 8\nvalue = [3, 5]"] ;
1 [label="fruit <= 0.5\nentropy = 1.0\nsamples = 6\nvalue = [3, 3]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="size <= 0.5\nentropy = 0.971\nsamples = 5\nvalue = [2, 3]"] ;
1 -> 2 ;
3 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
2 -> 3 ;
4 [label="scale <= 0.5\nentropy = 1.0\nsamples = 4\nvalue = [2, 2]"] ;
2 -> 4 ;
5 [label="entropy = 0.0\nsamples = 1\nvalue = [1, 0]"] ;
4 -> 5 ;
6 [label="entropy = 0.918\nsamples = 3\nvalue = [1, 2]"] ;
4 -> 6 ;
7 [label="entropy = 0.0\nsamples = 1\nvalue = [1, 0]"] ;
1 -> 7 ;
8 [label="entropy = 0.0\nsamples = 2\nvalue = [0, 2]"] ;
0 -> 8 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
}
这个文件可以通过dot.exe(下载链接https://graphviz.gitlab.io/_pages/Download/Download_windows.html)绘制图像。
(在安装目录的命令行窗口走dot -Tpng sample.dot -o sample.png语句,即可得到决策树图像)
Samples是此时dataSet的样本个数,那么还有2个问题,1.节点阈值是如何确定;2.节点上的value是什么意思?(叶节点上最终分类的标志是?)这个类库的决策树构造方法与数值有关。