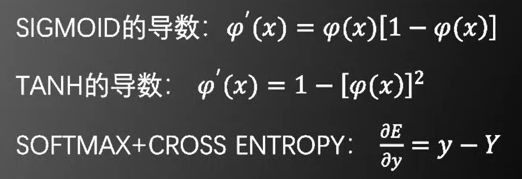机器学习笔记-03（人工神经网络解决兵王问题MATLAB程序）
机器学习笔记-03（人工神经网络解决兵王问题MATLAB程序）
大年三十，今年最后一个学习任务！依旧是比较简单的只是分析浙江大学机器学习课程中老师提供的程序。
一、程序分析
首先打开nn_testChess.m文件，程序中：数据读入的过程中首先看到27行和29行，在两类的多层神经网络中，两种情况：即要么是[1,0]要么是[0,1]
程序中37-39行将整个数据集分成了以下三个数据集：
- 训练数据集15%：利用训练数据集调整神经网路的参数；
- 验证数据集5%：用于验证调整是好是坏，从而决定程序是否退出；
- 测试数据集80%：训练结束后，用于总体测出神经网络的训练效果；
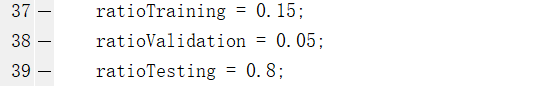
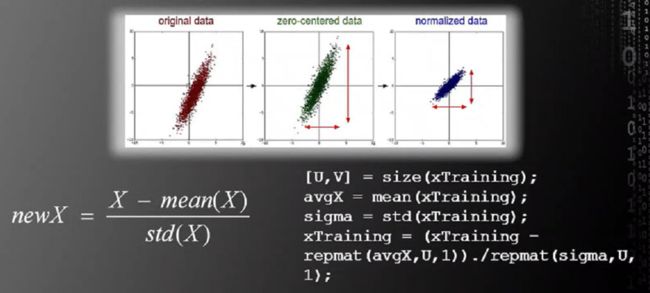
程序第53、65、76行分别表示的是对上述三个数据集进行归一化处理，均采用减掉均值除以方差的方法：
程序的第81行nn_create（目的：创建神经网络）中的含义如下：
程序的第86行：表示的是每个MINI-BATCH中有100个训练样本，并在92行中设置最大的训练轮次为10000轮
补充一下关于BATCH的内容：
随机梯度下降法（SGD）
随机梯度下降法是对于后向传播算法基本框架的改进的方法之一，由于
①每输入一个数据都更新网络所有参数，训练速度会非常慢；
② 如果梯度更新只依赖一个数据，那么这个数据带来的误差将会代入到每一个参数中；
可以采用以下两种方法：
（1）不用每输入一个样本就更新参数，而是输入一批样本（叫做BATCH或MINI-BATCH），求出这些样本的梯度平均值后，根据这个平均值改变参数；
- 其中BATCH或MINI-BATCH的训练样本值叫BATCH SIZE:取50-200
（2）对所有训练数据，根据BATCH SIZE分割为不同的BATCH，将这些BATCH依次送进神经网络，不断地更新梯度。按照BATCH遍历所有训练样本一次，称为一个EPOCH;
- 对于每个EPOCH，我们需要随机打乱所有训练样本中的次序，增加BATCH中训练样本的随机性；
程序第95-97表示：开始训练、测试平均的损失函数COST、在验证集上测试识别率accuracy；
训练过程中可以看到： - 损失函数COST↓
- 验证集上的识别率Accuracy↑
当COST已经下降到很小，识别率Accuracy增加到99%+时可以按CTRL+C退出循环，将107行拷贝出来在命令运行窗口，可以看到测试集上测试最后的训练效果。
二、深入程序内部
多层神经网络主要包括前向计算和后向传播两个步骤
(1)前向传播
前向传播计算步骤在nn_forward.m这个程序里面：
第10行以及第34-41行：从k-1层的输出到第k层的过程第k-1层的输出乘以权重矩阵w再加上偏置，最后经过非线性函数获得第k层输出
y = nn.W{k-1} * nn.a{k-1} + repmat(nn.b{k-1},1,m);%repmat(A,m,n)将A复制m×n块
switch nn.active_function%隐层激活函数选择
case 'sigmoid'
nn.a{k} = sigmoid(y);
case 'tanh'
nn.a{k} = tanh(y);
case 'relu'
nn.a{k} = max(y,0);
end
(2)后向传播
后向传播计算步骤在nn_backpropagation.m里
第6-13行详细介绍了求导过程：
switch nn.output_function
case 'sigmoid'
nn.theta{nn.depth} = -(batch_y-nn.a{nn.depth}) .* nn.a{nn.depth} .* (1 - nn.a{nn.depth});
case 'tanh'
nn.theta{nn.depth} = -(batch_y-nn.a{nn.depth}) .* (1 - nn.a{nn.depth}.^2);
case 'softmax'
nn.theta{nn.depth} = nn.a{nn.depth} - batch_y;
end
简便的求导公式有：
（3）多层神经网络参数更新过程
多层神经网络更新nn_applygradient.m这个程序中:
第18到20行：
if strcmp(nn.optimization_method, 'normal')
nn.W{k} = nn.W{k} - nn.learning_rate*nn.W_grad{k};
nn.b{k} = nn.b{k} - nn.learning_rate*nn.b_grad{k};
与梯度下降算法更新W和b更新一一对应
三、训练神经网络的建议和经验
（一）训练神经网络的三个经验
（1） 一般情况下，在训练集上的**目标函数的平均值(cost)**会随着训练的深人而不断减小，如果这个指标有增大情况，停下来。
有两种情况:
- 采用的模型不够复杂，以致于不能在训练集上完全拟合;
- 已经训练很好了
（2）分出一些验证集(Validation Set)：
训练的本质目标是在验证集上获取最大的识别率。 因此训练一段时间后，心须在验证集上测试识别率，保存使验证集上识别率最大的模型参数，作为最后的结果。
（3）注意调整学习率(Learning Rate)：
-
如果刚训练几步损失函数cost就增加，一般来说是学习率太高了;
-
如果每次cost变化很小，说明学习率太低
根据实际情况适度调整学习率是使神经网络快速、正确收敛的基础。
（二）训练神经网络的各种经验
（1） 目标函数可以加入正则项（regularization term):其中λ为权值衰减系数
不仅要让原来的目标函数尽可能的小，同时也要让正则项w的模尽可能的小，这样可以防止一些权值绝对值过大造成的过拟合情况；
- 加入了正则项的目标函数的前向计算：
if strcmp(nn.objective_function,'MSE')
nn.cost(s) = 0.5 / m * sum(sum((nn.a{k} - batch_y).^2)) + 0.5 * nn.weight_decay * cost2;
elseif strcmp(nn.objective_function,'Cross Entropy')
nn.cost(s) = -0.5*sum(sum(batch_y.*log(nn.a{k})))/m + 0.5 * nn.weight_decay * cost2;
- 加入了正则项的目标函数的后向传播：
%第二项是引入正则项后求导产生的，即正则项系数nn.weight_decay乘以w
nn.W_grad{nn.depth-1} = nn.theta{nn.depth}*nn.a{nn.depth-1}'/m + nn.weight_decay*nn.W{nn.depth-1};
(2) 训练数据归一化
保证训练数据的每一个维度落在一个相对固定的区间里
（3）参数w和b的初始化
随机梯度下降法的第一步是随机取所有的（w，b），但是在实际的应用中这样有可能会导致梯度消失，此时Wt+b的值很大，从而导致训练缓慢。因此我们要使Wt+b一开始就落在零的附近。
一种比较简单有效的方法是:
用下列代码分别对w和b进行初始化，避免梯度消失的现象：
nn.W{k} = 2*rand(height, width)/sqrt(width)-1/sqrt(width);%rand产生伪随机数矩阵，即W权重矩阵初始化
nn.b{k} = 2*rand(height, 1)/sqrt(width)-1/sqrt(width);%b阈值的初始化
（4）BATCH NORMALIZATION
论文:Batch normalization accelerating deep network training by reducing internal covariate shift(2015) 和参考笔记
基本思想:既然我们希望每-层获得的值都在0附近，从而避免梯度消失现象，那么我们为什么不直接把每一层的值做基于均值和方差的归一化呢?
具体见参考笔记中写的非常详细
（5）参数的更新策略
- 常规的更新策略是用随机梯度下降法，若（w，b）的每一个分量获得的梯度绝对值有大有小，一些情况下将会迫使优化路径变成z字形状。
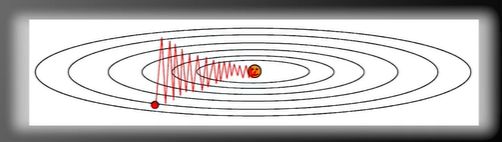
如图所示：由于垂直方向的梯度变化比水平方向的梯度变化的绝对值大，因此将使优化路径变成z字形状。需要耗费很长的时间，才能达到局部极值。
解决方法;ADAGRAD用于解决梯度变化不一致的情况，其主要的思路是将梯度的平方不断地累积，用归一化因子来规范最终的结果。
if strcmp(nn.optimization_method, 'AdaGrad')
nn.rW{k} = nn.rW{k} + nn.W_grad{k}.^2;
nn.rb{k} = nn.rb{k} + nn.b_grad{k}.^2;
nn.W{k} = nn.W{k} - nn.learning_rate*nn.W_grad{k}./(sqrt(nn.rW{k})+0.001);
nn.b{k} = nn.b{k} - nn.learning_rate*nn.b_grad{k}./(sqrt(nn.rb{k})+0.001);
- SGD的问题
由于SGD求梯度的策略过于随机，上一次和下一次采取的是完全不同BATCH的数据，那么将会出现优化方向随机化的现象。
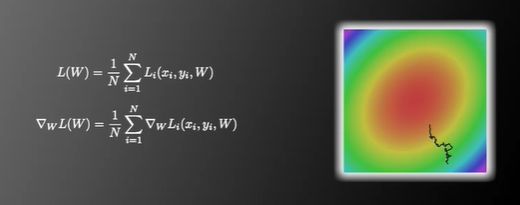
解决办法：引入动量Momentum的概念，其每次更新的时候不仅要考虑梯度的方向还要考虑上一次更新的方向，将这两个方向以人为规定的比例加权求和，获得最终的更新方向。
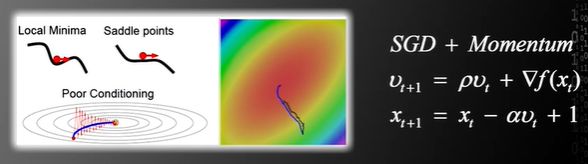
如图所示，这种方法可以使搜索路径变得光滑，降低搜索路径的随机性。 - 同时两个问题
Adam：结合了ADAGRAD和MOMENTUM,有效解决了梯度绝对值分量不平衡和梯度方向随机性，同时引入了逐渐降低梯度搜索步长的机制，用这种方法可以较快的找到极值点。
if strcmp(nn.optimization_method, 'Adam') %rho1=0.9,rho2 =0.999
rho1=0.9;
rho2 =0.999;
nn.sW{k} = rho1*nn.sW{k} + (1-rho1)*nn.W_grad{k};
nn.sb{k} = rho1*nn.sb{k} + (1-rho1)*nn.b_grad{k};
nn.sGamma{k} = rho1*nn.sGamma{k} + (1-rho1)*nn.Gamma_grad{k};
nn.sBeta{k} = rho1*nn.sBeta{k} + (1-rho1)*nn.Beta_grad{k};
nn.rW{k} = rho2*nn.rW{k} + (1-rho2)*nn.W_grad{k}.^2;
nn.rb{k} = rho2*nn.rb{k} + (1-rho2)*nn.b_grad{k}.^2;
nn.rBeta{k} = rho2*nn.rBeta{k} + (1-rho2)*nn.Beta_grad{k}.^2;
nn.rGamma{k} = rho2*nn.rGamma{k} + (1-rho2)*nn.Gamma_grad{k