吴恩达深度神经网络笔记—残差网络ResNet
残差网络的搭建
利用上周学的keras框架，搭建一个深层次的卷积网络，越深的网络在实际上非常难以训练。残差网络就是为了解决深网络的难以训练的问题的。
首先我们要实现基本的残差块。再将这些残差块放在一起，实现并训练用于图像分类的神经网络。
导包
import numpy as np
from keras import layers
from keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D
from keras.models import Model, load_model
from keras.preprocessing import image
from keras.utils import layer_utils
from keras.utils.data_utils import get_file
from keras.applications.imagenet_utils import preprocess_input
import pydot
from IPython.display import SVG
from keras.utils.vis_utils import model_to_dot
from keras.utils import plot_model
from resnets_utils import *
from keras.initializers import glorot_uniform
import scipy.misc
from matplotlib.pyplot import imshow
%matplotlib inline
import keras.backend as K
tf.compat.v1.disable_eager_execution()
K.set_image_data_format('channels_last')
K.set_learning_phase(1)
深层网络的好与坏
好处就是它能够完成很复杂的功能，它能够从边缘（浅层）到非常复杂的特征（深层）中不同的抽象层次的特征中学习。
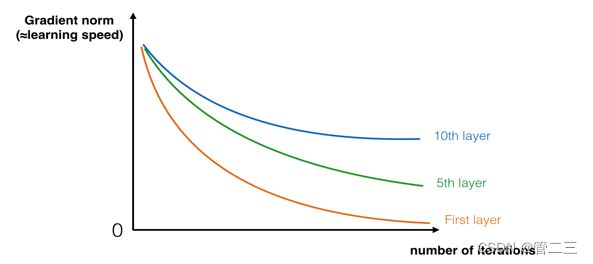
坏处就在于训练的时候会产生梯度消失，非常深的网络通常会有一个梯度信号，该信号会迅速的消退，从而使得梯度下降变得非常缓慢。
如这张图所示：
构建一个残差网络
在残差网络中，一个“捷径（shortcut）”或者说“跳跃连接（skip connection）”允许梯度直接反向传播到更浅的层，如下图：
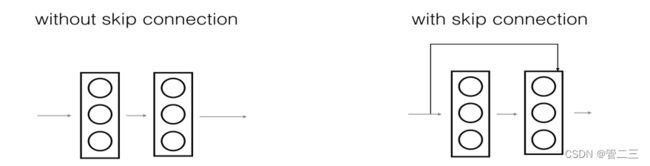
使用捷径的方式使得每一个残差块能够很容易学习到恒等式功能，这意味着我们可以添加很多的残差块而不会损害训练集的表现。
残差块有两种类型，主要取决于输入输出的维度是否相同。
恒等块
恒等块是残差网络使用的的标准块，输入的激活值和输出的激活值维度相同。
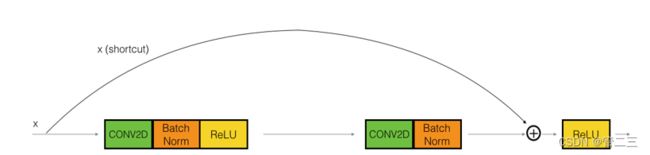曲线路径是“捷径”，直线路径是主路径。把CONV2D 与 ReLU包含到了每个步骤中，为了提升训练的速度，我们在每一步也把数据进行了归一化（BatchNorm），Keras框架已经实现了这些东西，调用BatchNorm只需要一行代码。
实践中我们跳跃连接会跳过3个隐藏层而不是两个：
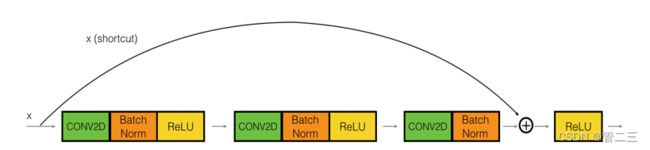实现残差网络的恒等块有4步：
- 主路径的第一部分：
第一个CONV2D有F1个过滤器，其大小为（1，1），步长为（1，1），使用填充方 式为“valid”，命名规则为conv_name_base + ‘2a’，使用0作为随机种子为其初始化。
第一个BatchNorm是通道的轴归一化，其命名规则为bn_name_base + ‘2a’。
接着使用ReLU激活函数，它没有命名也没有超参数。 - 主路径的第二部分：
第二个CONV2D有F2个过滤器，其大小为（f，f），步长为（1，1），使用填充方 式为“same”，命名规则为conv_name_base + ‘2b’，使用0作为随机种子为其初始化。
第一个BatchNorm是通道的轴归一化，其命名规则为bn_name_base + ‘2b’。
接着使用ReLU激活函数，它没有命名也没有超参数。 - 主路径的第三部分：
第三个CONV2D有F3个过滤器，其大小为（1，1），步长为（1，1），使用填充方 式为“valid”，命名规则为conv_name_base + ‘2c’，使用0作为随机种子为其初始化。
第三个BatchNorm是通道的轴归一化，其命名规则为bn_name_base + ‘2c’。 - 将捷径与输入加在一起使用ReLU激活函数
def identity_block(X, f, filters, stage, block):
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
F1, F2, F3 = filters
X_shortcut = X
X = Conv2D(filters = F1, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
X = Activation('relu')(X)
X = Conv2D(filters = F2, kernel_size = (f, f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
X = Activation('relu')(X)
X = Conv2D(filters = F3, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)
X = Add()([X,X_shortcut])
X = Activation('relu')(X)
return X
测试：
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as test:
np.random.seed(1)
A_prev = tf.compat.v1.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = identity_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
test.run(tf.compat.v1.global_variables_initializer())
out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
print("out = " + str(out[0][1][1][0]))
结果：
out = [0. 0. 1.3454674 2.0318177 0. 1.3246754]
卷积块
如图，当输入输出维度不一致时，利用卷积块，不同之处在于捷径上是一个卷积层。
它的主要作用是仅仅应用（学习后的）线性函数来减少输入的维度，以便在后面的加法步骤中的维度相匹配。
实现残差网络的卷积块有5步：
- 主路径的第一部分：
第一个CONV2D有F1个过滤器，其大小为（1，1），步长为（s，s），使用填充方 式为“valid”，命名规则为conv_name_base + ‘2a’，使用0作为随机种子为其初始化。
第一个BatchNorm是通道的轴归一化，其命名规则为bn_name_base + ‘2a’。
接着使用ReLU激活函数，它没有命名也没有超参数。 - 主路径的第二部分：
第二个CONV2D有F2个过滤器，其大小为（f，f），步长为（1，1），使用填充方 式为“same”，命名规则为conv_name_base + ‘2b’，使用0作为随机种子为其初始化。
第一个BatchNorm是通道的轴归一化，其命名规则为bn_name_base + ‘2b’。
接着使用ReLU激活函数，它没有命名也没有超参数。 - 主路径的第三部分：
第三个CONV2D有F3个过滤器，其大小为（1，1），步长为（s，s），使用填充方 式为“valid”，命名规则为conv_name_base + ‘2c’，使用0作为随机种子为其初始化。
第三个BatchNorm是通道的轴归一化，其命名规则为bn_name_base + ‘2c’。 - 捷径有F3个过滤器，其大小为（1，1），步长为（s，s），使用填充方式为“valid”，命名规则为conv_name_base + ‘1’；通道的轴归一化，其命名规则为bn_name_base + ‘1’
- 将捷径与输入加在一起使用ReLU激活函数
def convolutional_block(X, f, filters, stage, block, s = 2):
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
F1, F2, F3 = filters
X_shortcut = X
X = Conv2D(filters = F1, kernel_size = (1, 1), strides = (s,s), padding = 'valid', name = conv_name_base + '2a', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2a')(X)
X = Activation('relu')(X)
X = Conv2D(filters = F2, kernel_size = (f, f), strides = (1,1), padding = 'same', name = conv_name_base + '2b', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2b')(X)
X = Activation('relu')(X)
X = Conv2D(filters = F3, kernel_size = (1, 1), strides = (1,1), padding = 'valid', name = conv_name_base + '2c', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = bn_name_base + '2c')(X)
X_shortcut = Conv2D(filters = F3, kernel_size = (1, 1), strides = (s,s), padding = 'valid', name = conv_name_base + '1', kernel_initializer = glorot_uniform(seed=0))(X_shortcut)
X_shortcut = BatchNormalization(axis = 3, name = bn_name_base + '1')(X_shortcut)
X = Add()([X,X_shortcut])
X = Activation('relu')(X)
return X
测试：
tf.compat.v1.reset_default_graph()
with tf.compat.v1.Session() as test:
np.random.seed(1)
A_prev = tf.compat.v1.placeholder("float", [3, 4, 4, 6])
X = np.random.randn(3, 4, 4, 6)
A = convolutional_block(A_prev, f = 2, filters = [2, 4, 6], stage = 1, block = 'a')
test.run(tf.compat.v1.global_variables_initializer())
out = test.run([A], feed_dict={A_prev: X, K.learning_phase(): 0})
print("out = " + str(out[0][1][1][0]))
结果：
out = [0. 0. 0. 0.8929655 0. 0.19882727]
构建残差网络（50层）
如图，这个50层的网络的细节如下：
- 对输入数据进行0填充，padding =（3,3）
- 卷积层有64个过滤器，其维度为（7，7），步伐为（2，2），命名为“conv1”
规范层（BatchNorm）对输入数据进行通道轴归一化。
最大值池化层使用一个（3，3）的窗口和（2，2）的步伐。 - 卷积块使用f=3个大小为[64，64，256]的过滤器，f=3，s=1,block=“a”
2个恒等块使用三个大小为[64，64，256]的过滤器，f=3，block=“b”、“c” - 卷积块使用f=3个大小为[128,128,512]的过滤器，f=3，s=2,block=“a”
3个恒等块使用三个大小为[128,128,512]的过滤器，f=3，block=“b”、“c”、“d” - 卷积块使用f=3个大小为[256,256,1024]的过滤器，f=3，s=2,block=“a”
5个恒等块使用三个大小为[256,256,1024]的过滤器，f=3，block=“b”、“c”、“d”、“e”、“f” - 卷积块使用f=3个大小为[512,512,2048]的过滤器，f=3，s=2,block=“a”
2个恒等块使用三个大小为[256,256,2048]的过滤器，f=3，block=“b”、“c” - 均值池化层使用维度为（2,2）的窗口，命名为“avg_pool”
- 展开操作没有任何超参数以及命名
- 全连接层（密集连接）使用softmax激活函数，命名为"fc" + str(classes)
def ResNet50(input_shape = (64, 64, 3), classes = 6):
X_input = Input(input_shape)
X = ZeroPadding2D((3, 3))(X_input)
X = Conv2D(64, (7, 7), strides = (2, 2), name = 'conv1', kernel_initializer = glorot_uniform(seed=0))(X)
X = BatchNormalization(axis = 3, name = 'bn_conv1')(X)
X = Activation('relu')(X)
X = MaxPooling2D((3, 3), strides=(2, 2))(X)
X = convolutional_block(X, f = 3, filters = [64, 64, 256], stage = 2, block='a', s = 1)
X = identity_block(X, 3, [64, 64, 256], stage=2, block='b')
X = identity_block(X, 3, [64, 64, 256], stage=2, block='c')
X = convolutional_block(X, f = 3, filters = [128,128,512], stage = 3, block='a', s = 2)
X = identity_block(X, 3, [128,128,512], stage=3, block='b')
X = identity_block(X, 3, [128,128,512], stage=3, block='c')
X = identity_block(X, 3, [128,128,512], stage=3, block='d')
X = convolutional_block(X, f = 3, filters = [256, 256, 1024], stage = 4, block='a', s = 2)
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='b')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='c')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='d')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='e')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='f')
X = identity_block(X, 3, [256, 256, 1024], stage=4, block='g')
X = convolutional_block(X, f = 3, filters = [512, 512, 2048], stage = 5, block='a', s = 2)
X = identity_block(X, 3, [512, 512, 2048], stage=5, block='b')
X = identity_block(X, 3, [512, 512, 2048], stage=5, block='c')
X = AveragePooling2D(pool_size=(2,2),padding="same")(X)
X = Flatten()(X)
X = Dense(classes, activation='softmax', name='fc' + str(classes), kernel_initializer = glorot_uniform(seed=0))(X)
model = Model(inputs = X_input, outputs = X, name='ResNet50')
return model
实例化模型：
model = ResNet50(input_shape = (64, 64, 3), classes = 6)
编译：
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
加载数据集：
X_train_orig, Y_train_orig, X_test_orig, Y_test_orig, classes = load_dataset()
# Normalize image vectors
X_train = X_train_orig/255.
X_test = X_test_orig/255.
# Convert training and test labels to one hot matrices
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
测试集：
number of training examples = 1080
number of test examples = 120
X_train shape: (1080, 64, 64, 3)
Y_train shape: (1080, 6)
X_test shape: (120, 64, 64, 3)
Y_test shape: (120, 6)
运行模型两代，batch=32，每代大约3分钟左右。
model.fit(X_train, Y_train, epochs = 2, batch_size = 32)
评估准确率
preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))
结果：
Loss = 3.2275264898935956
Test Accuracy = 0.16666667
可以选择继续训练RESNET。当我们训练20代时，我们得到了更好的性能，但是在得在CPU上训练需要一个多小时。使用GPU的话，博主已经在手势数据集上训练了自己的RESNET50模型的权重，你可以使用下面的代码载并运行博主的训练模型，加载模型可能需要1min。
model = load_model('ResNet50.h5')
preds = model.evaluate(X_test, Y_test)
print ("Loss = " + str(preds[0]))
print ("Test Accuracy = " + str(preds[1]))
准确率：
Loss = 0.5301782846450805
Test Accuracy = 0.8666667