机器学习笔记——极大似然估计与最大后验概率估计

目录

数据与概率模型

机器学习领域的一个关键概念——事件发生的不确定性。概率论 为这种不确定性的量化和操纵提供了框架，成为机器学习的核心基础之一。
基于现实世界中所发生现象的任何实际模型，必须要考虑到 随机性 的可能。也就是说，我们所关注的信息可能是事先不可预料的。但是，经过大量重复试验，这种现象往往存在某种 规律性。
因此，表述该现象的模型实质上是概率性的 $\to$ 这种模型被称为 概率模型。

示例：投掷一枚质地均匀的硬币。
排除硬币站立等极特殊情况，样本空间$\mathcal{S}$中共包含两种情况：
$$\mathcal{S}=\{Head,Tail\}$$
其中$Head$表示“硬币正面朝上”，$Tail$表示“硬币反面朝上”。
我们发现，投掷硬币这个试验，确实满足上述两种属性：

• 在投掷硬币试验结果出现之前，我们没有办法事先预料硬币是正面朝上还是反面朝上；
• 在大量重复试验过程中，我们发现 规律：硬币正面朝上和反面朝上的次数相差不大。

相关符号定义

我们定义$\mathcal{X}$为大量数据试验产生的数据集合(data)：

• 定义该数据集合共包含$N$个数据样本；

• 样本维度 数量定义为$p$；
  样本维度，通俗点讲，即使用 一组数值描述数据样本特征，而这组数值的数量即样本维度。$\mathcal{S}$中的任意一个样本都可以使用这组数值进行表示。
  示例：

  如果我们想要统计 收入与人之间 的关联关系，在收集样本时，我们对样本属性进行划分：
  性别：0 - 男 \ 1 - 女；
  年龄：
  学历：0 - 高中\ 1 - 专科\ 2 - 本科\ 3 - 硕士\ 4 - 博士
  从事行业：0 - IT行业\ 1 - 金融\ 2 - 服务\ 3 - 管理…
  从事年限：0 - 0-1年\ 1 - 1-3年\ 2 - 3-5年\ 3 - 5年以上
  婚姻情况：0 - 已婚\ 1 - 未婚
  月收入情况：0 - 5000以下\ 1 - 5000-8000\ 2 - 8000-10000\ 3 - 10000以上
  现有一个样本描述如下：
  一个27岁姑娘，硕士，从事金融行业1年，未婚，月收入9200
  使用 向量 表示该样本的特征信息：
  $$[1,27,3,1,0,1,2]$$
  以上我们从 7个维度 对一个样本进行统计，在数据集合中任意一个样本都可以统计到该特征。

回归正题，使用 数学符号 对数据集合$\mathcal{X}$进行表示：
$$\mathcal{X}=\left(\begin{array}{c}{x}^{(1)}\\ x^{(2)}\\ x^{(3)}\\ ⋮\\ x^{(N)}\end{array}\right)$$
其中$N$表示数据集合$\mathcal{X}$中包含的样本数量；每一个样本根据 样本维度 可以进行如下表示($x_1$示例)：
$$x^{(1)}=\left(\begin{array}{c}{x}_1^{(1)},x_2^{(1)},x_3^{(1)},...,x_p^{(1)}\end{array}\right)$$
可以将其理解成：使用关于样本$x^{(1)}$的$p$个维度的不同结果$x_1^{(1)},x_2^{(1)},x_3^{(1)},...,x_p^{(1)}$对$x^{(1)}$进行表示。
综上，将样本数量与维度结合，关于样本集合$\mathcal{X}$的表示如下($N\times p$ 的二维矩阵)：
$$\mathcal{X}=\left(\begin{array}{c}{x}^{(1)}\\ x^{(2)}\\ x^{(3)}\\ ⋮\\ x^{(N)}\end{array}\right)={\left(\begin{array}{c}{x}_1^{(1)},x_2^{(1)},\cdots ,x_p^{(1)}\\ x_1^{(2)},x_2^{(2)},\cdots ,x_p^{(2)}\\ x_1^{(3)},x_2^{(3)},\cdots ,x_p^{(3)}\\ ⋮\\ x_1^{(N)},x_2^{(N)},\cdots ,x_p^{(N)}\end{array}\right)}_{N\times p}$$

我们将 数据本身 看做概率模型，设该模型的参数(parameter)为$\theta$。
某一样本$x$可以进行如下表示：
$$x\sim P(x;\theta )$$
可以将其理解成：在$P(x;\theta )$的概率分布下，以模型参数$\theta$产生一个又一个的相互独立的$x$样本，构成$\mathcal{X}$数据集合。
样本间相互独立原因是‘每一个样本’均是在相同概率分布下，通过重复试验产生的结果，因此各结果之间不存在关联关系。
例如：投掷两次同一个硬币，第一次正面朝上和第二次正面朝上的概率没有任何关系。

机器学习的核心是通过样本集合$\mathcal{X}$学习概率模型的参数$\theta$，并基于$\theta$对新样本进行预测。

频率学派角度看待机器学习问题

频率学派认为：概率分布$P(x;\theta )$中的参数$\theta$是一个 未知的常量。数据集合$\mathcal{X}$本身是随机变量(Random Variable)。

这里引用黑格尔的一句话很贴切：存在即合理。结合$x\sim P(x;\theta )$，既然$x$是基于参数$\theta$的概率分布$P(x;\theta )$产生出来的样本，每一个样本$x$的存在都有它的道理。

因此，频率学派通过大量试验产生的样本集合$\mathcal{X}$将概率模型参数$\theta$估计出来。常用的方法是 极大似然估计(Maximum Likelihood Estimate,MLE)。

极大似然估计

极大似然估计表示如下：
$${\theta }_{MLE}=\underset{\theta }{\mathrm{argmax}}P(X;\theta )$$
从字面意思来讲，求得一个具体的参数$\theta$,使得数据集合$\mathcal{X}$的概率最大。而 数据集合$\mathcal{X}$的概率同样可以表示为数据集合内样本的联合概率分布。公式表示如下：
$$P(X;\theta )=P(x^{(1)},x^{(2)},...,x^{(N)};\theta )$$

通常情况下，我们也将极大似然估计表示为如下形式：
$${\theta }_{MLE}=\underset{\theta }{\mathrm{argmax}}\log P(X;\theta )$$
为什么要加一个$\log$函数呢？
上面提到，从$P(x;\theta )$概率分布中产生相互独立的样本$x$,我们称 $x$服从于$P(x;\theta )$且独立同分布。数学符号记作：
$$x\stackrel{\text{iid}}{\sim }P(x;\theta )$$
因此，数据集合$\mathcal{X}$产生的联合概率分布$P(X;\theta )$表示如下：
$$P(X;\theta )=\prod _{i=1}^{N}P(x_i;\theta )$$
我们在处理连乘过程中是非常消耗运算资源的，我们给$P(X;\theta )$添加一层$\log$函数，重新观察运算过程：
$$\begin{array}{rl}\log P(X;\theta )& =\log \prod _{i=1}^{N}P(x_i;\theta )\\ & =\sum _{i=1}^N\log P(x_i;\theta )\end{array}$$
我们发现，$\log$函数将极大似然估计中的乘法运算替换成加法运算，有效降低了运算资源的消耗；
个人理解：若干个概率值相乘(有多少个样本，就有多少个概率结果)，它的结果都会无限趋近于零，最终可能会达到计算机能够判定的临界值 -> 这给计算机的计算和判定带来负担，并存在判定错误的隐患。
我们同样发现，新结果中的$P(x_i\mid \theta )$套了一层$\log$函数，这个$\log$是否对极大似然估计结果产生影响呢？
$\log$函数图像如下图所示：

我们发现：

• $\log$函数属于单调递增函数，因此$\log P(x_i;\theta )$中$\log$函数的添加对极大似然估计结果的单调性没有影响。
• 由于$P(x_i;\theta )$是概率结果，其值域为$[0,1]$,而$\log$映射后的结果值域为$(-\infty ,0]$,其映射区间明显增大。
• 相比于${\prod }_{i=1}^{N}P(x_i;\theta )$，${\sum }_{i=1}^N\log P(x_i;\theta )$结果存在上界(最大值) $\to \le 0$ 恒成立。

贝叶斯学派角度看待机器学习问题

相比于频率学派，贝叶斯学派的观点是：$P(x\mid \theta )$中的 参数$\theta$不是一个固定结果，而是和$P(x\mid \theta )$一样，都是随机变量，且服从某一概率分布。
数学符号表达为：
$$\theta \sim p(\theta )$$
通常情况下，称$p(\theta )$为 先验分布(Prior Distributions)。
使用贝叶斯定理，将先验分布、后验分布(Posterior Distributions)、似然(Likelihood)联系起来。
观察 贝叶斯定理：
$$P(\theta \mid X)=\frac{P(X\mid \theta )\cdot P(\theta )}{P(X)}$$
其中：

• $P(\theta \mid X)$是后验分布，是基于对样本$X$采样之后得到的分布；
• $P(\theta )$是先验分布，即对样本$X$进行 采样之前，通过观察，人们也会对$\theta$有一些认识。
• $P(X\mid \theta )$是似然，以基于参数$\theta$的概率分布$P(X\mid \theta )$生成样本$X$。
• 分母部分称为配分函数(Partition function)，它本质上是一个边缘概率(如果是离散型随机变量，使用$\sum$进行表达)：
  $$\begin{array}{r}P(X)=\{\begin{array}{l}{\int }_{\theta }P(X\mid \theta )P(\theta )d\theta \\ {\sum }_{\theta }P(X\mid \theta )P(\theta )\end{array}\end{array}$$

最大后验概率估计

贝叶斯学派对于参数$\theta$分布的常用估计方法：最大后验概率(Maximum A Posteriori)估计
其本意即找到一个后验概率$P(\theta \mid X)$最优结果所对应参数$\theta$的分布作为最优估计。
$$\begin{array}{rl}{\theta }_{MAP}& =\underset{\theta }{\mathrm{argmax}}P(\theta \mid X)\\ & =\underset{\theta }{\mathrm{argmax}}\frac{P(X\mid \theta )\cdot P(\theta )}{P(X)}\end{array}$$
观察上式的分母$P(X)$：其本质上就是一个关于$X$的 边缘概率，而$\theta$是一个积分常量。因此$P(X)$和$\theta$无关。(该部分可参考动态规划求解强化学习任务——策略评估[解析解]中的条件概率密度积分)
$${\int }_{\theta }P(X\mid \theta )P(\theta )d\theta ={\int }_{\theta }P(X,\theta )d\theta =P(X)$$
因此，上式可以等价为：
$${\theta }_{MAP}\propto \underset{\theta }{\mathrm{argmax}}P(X\mid \theta )\cdot P(\theta )$$

贝叶斯估计及其弊端

实际上，最大后验概率估计并 不是 标准的贝叶斯学派对于参数$\theta$的估计方法，贝叶斯学派方法本质上就是要求$P(\theta \mid X)$这个分布本身——贝叶斯估计(Bayesian Estimation)
$$P(\theta \mid X)=\frac{P(X\mid \theta )\cdot P(\theta )}{\int P(X\mid \theta )P(\theta )d\theta }$$

贝叶斯估计自身存在弊端，其核心问题在于：要将$P(X)$强行求解。
回顾该式：
$$P(X)={\int }_{\theta }P(X\mid \theta )P(\theta )d\theta$$
由于$\theta$是一个分布，该分布是存在维度的。如果是在低维状态下，积分可以较容易地计算出来，但是如果$\theta$维度较高，这个积分将变得 异常复杂。从而使对后验分布$P(\theta \mid X)$进行精确计算是几乎无法实现的。因此，可以采用一些近似计算来获取后验分布。

常见的近似求解方法：

• 确定性近似 $\to$ 变分推断(Variational Inference,VI)；
• 随机性近似 $\to$ 马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo,MCMC)

实例了解极大似然估计和最大后验概率的区别

回顾最大后验概率估计公式：
$${\theta }_{MAP}\propto \underset{\theta }{\mathrm{argmax}}P(X\mid \theta )\cdot P(\theta )$$
和极大似然估计一样，将$\log$添加到上式中：
$$\begin{array}{rl}{\theta }_{MAP}& \propto \underset{\theta }{\mathrm{argmax}}\log P(X\mid \theta )\cdot P(\theta )\\ & \propto \underset{\theta }{\mathrm{argmax}}\log P(X\mid \theta )+\log P(\theta )\end{array}$$
和极大似然估计相比，最大后验概率估计多了一项$\log P(\theta )$；
$${\theta }_{MLE}=\underset{\theta }{\mathrm{argmax}}\log P(X\mid \theta )$$
因此，最大后验概率估计不仅要让$\log P(X\mid \theta )$达到最大，而且还要让$\log P(\theta )$也要达到最大。从而出现 最大后验估计能够影响参数的值朝着先验分布偏移。

使用投掷硬币试验进行说明：
取一个质地均匀的硬币，投掷10次，投掷结果如下：

	正面朝上	反面朝上
次数	7	3

设：投掷硬币正面朝上的概率为$p$,则反面朝上的概率为$(1-p)$。当前试验使用极大似然估计计算结果：
$$P(X\mid \theta )=(p{)}^7\times (1-p{)}^3$$
对上述结果进行$\log$操作：
$$\begin{array}{rl}\ln (P(X\mid \theta ))& =\ln ((p{)}^7\times (1-p{)}^3)\\ & =7\ln (p)+3\ln (1-p)\end{array}$$
目的是求解$\ln (P(X\mid \theta ))$的最大值，对上式进行求导操作：
$$\begin{array}{r}{\ln }^{\prime }(P(X\mid \theta ))=0\\ \to \frac{7}{p}+\frac{3}{p-1}=0\\ \to p=0.7\end{array}$$

在实际运算中同样可以验证这个信息：
代码如下：

def f(x):
    return (x ** 7) * ((1 - x) ** 3)
    
if __name__ == '__main__':
    x = np.linspace(0,1,100)
    y = [f(i) for i in x]
    plt.plot(x,y)
    plt.plot([0.7 for _ in y])
    plt.show()

返回结果如下。我们发现，确实在0.7的位置取到最值：

至此，使用极大似然估计方法计算得到 投掷硬币正面朝上的概率为0.7。
如果试验之前已经知道该该硬币是质地均匀的：
$$P(Head)=P(Tail)=0.5$$
由于最大后验概率估计中 $\theta$是一个分布而不是具体结果，因此假设$p(\theta )$是一个均值为0.5，方差为0.1的高斯分布，即：
$$\begin{array}{rl}P(\theta )& =\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\\ & =\frac{1}{0.1\times \sqrt{2\pi }}{e}^{-\frac{(p-0.5{)}^2}{0.02}}\end{array}$$

根据最大后验概率估计，计算函数的最值：
$$\begin{array}{rl}\ln (P(x\mid \theta )P(\theta ))& =\ln (P(x\mid \theta ))+\ln (P(\theta ))\\ & =\ln ((p{)}^7\times (1-p{)}^3)+\ln (\frac{1}{0.1\times \sqrt{2\pi }}{e}^{-\frac{(p-0.5{)}^2}{0.02}})\end{array}$$
对该结果求导，可以得到如下式子：
$$\frac{3}{p-1}+\frac{7}{p}-100\times (p-\frac{1}{2})$$
对该求导结果求解零点，我们这里使用代码实现(解一元三次方程费眼睛~)

def diver_opera(x):
    return (3 / (x - 1)) + (7 / x) - (100 * (x - 0.5))

if __name__ == '__main__':
    x = np.linspace(0,1,500)
    dy = [diver_opera(i) for i in x]
    plt.plot(x,dy)
    plt.plot(x,[0 for i in x])
    plt.show()

我们发现，零点位置横坐标约为$p=0.558$。即 通过最大后验概率估计投掷硬币正面朝上的概率为0.558。直接求解$P(X\mid \theta )P(\theta )$同样能够看到该结果。代码如下：

import math
def norm(x):
    return (1 / (0.01 * math.sqrt(2 * math.pi))) * math.exp(-1 * (((x - 0.5) ** 2) / 0.02))

def f(x):
    return (x ** 7) * ((1 - x) ** 3) * norm(x)

if __name__ == '__main__':
    x = np.linspace(0,1,500)
    y_ = [f(i) for i in x]
    plt.plot(x,y_)
    plt.plot([0.558 for i in y_],y_)
    plt.show()

图像结果如下：

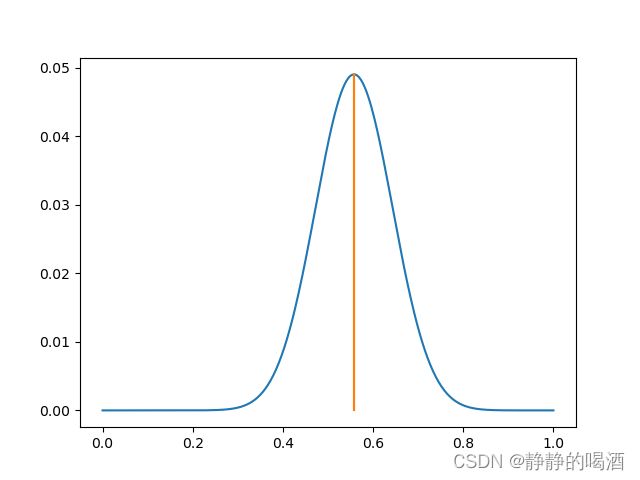
但是随着试验次数的增加，极大似然估计的计算结果会越来越准确，而先验知识能够影响的部分也越来越小。
基于上述例子，若改成投掷1000次硬币，正面朝上和反面朝上结果分布如下：

	正面朝上	反面朝上
次数	700	300

在不修改先验分布$P(\theta )$的前提下，依然使用极大似然估计和最大后验概率估计对$\theta$进行求解：
代码如下：

import math

def norm(x):
    return (1 / (0.01 * math.sqrt(2 * math.pi))) * math.exp(-1 * (((x - 0.5) ** 2) / 0.02))
def mle(x):
    return (x ** 700) * ((1 - x) ** 300)
def map_operation(x):
    return (x ** 700) * ((1 - x) ** 300) * norm(x)

if __name__ == '__main__':
    x = np.linspace(0,1,500)
    y_mle = [mle(i) for i in x]
    y_map = [map_operation(i) for i in x]
    plt.plot(x,y_map)
    plt.plot(x,y_mle)
    plt.show()

图像结果如下(橙色线是$MLE$结果，蓝色线是$MAP$结果，它们最大值对应的横坐标相差不大($MAP$结果要更小一点点))：

我们发现，最大后验概率估计貌似不起作用了，即随着重复试验次数的增加，先验知识的影响在减小。
可能这个硬币确实是个质地不均匀的硬币~
$${\theta }_{MLE}=0.7,{\theta }_{MAP}=0.695$$

总结：
相比于极大似然估计的操作，最大后验概率估计相当于在极大似然估计的基础上，乘以一个关于参数$\theta$的先验认识$P(\theta )$，而$P(\theta )$的作用就是 影响参数结果朝着$P(\theta )$方向偏移($0.7\stackrel{0.5}{⟶}0.558$)，但随着重复试验次数的增多，先验分布的影响力在逐渐减小，但先验分布仍然是 很有必要的。

下一节将介绍高斯分布。

相关参考：
机器学习-白板推导系列(一)-开篇
最大似然估计，最大后验估计以及贝叶斯估计的理解整理