PyTorch教程(2)概率分布
在像PyTorch这样的图形计算平台中,概率和随机变量是计算中不可分割的一部分。理解概率和相关概念是至关重要的。本章涵盖了概率分布和使用PyTorch实现,并解释了测试结果。
在概率和统计中,随机变量结果依赖于一个纯粹的随机现象。概率分布有不同的类型,包括正态分布,二项分布,多项分布,伯努利分布。每种统计分布都有自己的特性。
torch.distributions模块包含概率分布和抽样函数。在计算图中,每种分布类型都有其自身的重要性。distributions模块包含二项式,伯努利分布,贝塔分布,分类分布,指数分布,正态分布,泊松分布。
张量
权值初始化是训练神经网络和任何深度学习模型(如卷积神经网络(CNN)、深度神经网络(DNN)和递归神经网络(RNN))的重要任务。问题始终在于如何初始化权重。
权值初始化可以通过使用各种方法完成,包括随机权值初始化。基于分布的权重初始化可以使用均匀分布、伯努利分布、多项分布和正态分布。接下来将解释如何使用PyTorch来实现它。
要执行神经网络,需要向反向传播层传递一组初始权值,以计算损失函数(因此,可以计算精度)。方法的选择取决于数据类型、任务和模型所需的优化方法。这里我们将看到所有类型的初始化权值的方法。
如果用例需要复制相同的结果以保持一致性,那么就需要设置一个手动种子。
import torch
torch.manual_seed(1234)
种子值可以定制。这个随机数纯粹是随机产生的。随机数也可以从统计分布中产生。连续均匀分布的概率密度函数定义为:
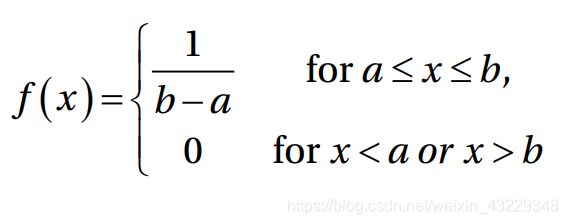
关于x的函数有两个点,a和b,其中a是起点,b是终点。在连续均匀分布中,每个数被选上的机会相等。在下面的例子中,起始值为0,结束值为1;在这两位数字之间,所有16个元素都是随机选择的。
import torch
torch.manual_seed(1234)
print(torch.Tensor(4,4).uniform_(0,1))
# tensor([[0.0290, 0.4019, 0.2598, 0.3666],
# [0.0583, 0.7006, 0.0518, 0.4681],
# [0.6738, 0.3315, 0.7837, 0.5631],
# [0.7749, 0.8208, 0.2793, 0.6817]])
在统计学中,伯努利分布被认为是离散概率分布,它有两种可能的结果。如果事件发生,则值为1,如果事件没有发生,则值为0。
对于离散概率分布,我们用概率质量函数代替概率密度函数。概率质量函数就像下面的公式。

在伯努利分布中,我们通过考虑大小为4x4的均匀分布来创建样本张量,其矩阵格式如下。
import torch
print(torch.bernoulli(torch.Tensor(4,4).uniform_(0,1)))
# tensor([[0., 1., 0., 1.],
# [0., 0., 0., 1.],
# [1., 1., 0., 0.],
# [1., 0., 1., 1.]])
下面的脚本定义了从多项分布生成样本随机值。
# torch.multinomial(input, num_samples,replacement=False, out=None) → LongTensor
# n_samples是取值次数
# replacement指的是取样时是否是有放回的取样,True是有放回,False无放回。
# 输出的张量是每一次取值时input张量对应行的下标。
import torch
x = torch.Tensor([10, 10, 13, 10, 34, 45, 65, 67, 34])
print(x)
s = torch.multinomial(x, 3)
print(s)
# tensor([10., 10., 13., 10., 34., 45., 65., 67., 34.])
# tensor([6, 5, 3])
print(x[s])
# tensor([65., 45., 10.])
s2 = torch.multinomial(x, 3, replacement=True)
print(s2)
# tensor([5, 8, 0])
正态分布的权值初始化是一种用于拟合神经网络、拟合深度神经网络以及CNN和RNN的方法。 让我们来看看如何从正态分布中生成一组随机权值。
import torch
print(torch.normal(mean=torch.arange(1.,11.),std=torch.arange(1, 0, -0.1)))
print(torch.normal(mean=0.5,std=torch.arange(1, 0, -0.1)))
# tensor([0.6081, 2.0959, 3.3777, 3.2333, 5.7116, 5.8800, 6.8375, 7.7534, 8.6826, 9.9325])
# tensor([ 1.3883, 2.3341, 1.6991, -0.3810, 0.2032, 0.6049, -0.0235, 0.1430, 0.7984, 0.4316])
可变张量
PyTorch中的变量是什么?它是如何定义的? 什么是PyTorch中的随机变量?
在PyTorch中,算法被表示为一个计算图。变量被认为是围绕张量对象、相应的梯度以及对创建它的函数的引用的表示。 为简单起见,梯度被认为是函数的斜率。 函数的斜率可以通过对函数中存在的参数求导来计算。
PyTorch变量是计算图中的一个节点,它存储数据和梯度。 在训练神经网络模型时,每次迭代后,我们需要计算损失函数相对于模型参数,如权重和偏差的梯度。 之后,我们通常使用梯度下降算法更新权值。
下面的脚本显示了如何使用变量创建计算图的示例。 有三个变量x1, x2和x3带有a = 12和b = 23生成的随机点。 图的计算只涉及乘法和加法,并显示带有梯度的最终结果。
在PyTorch中使用Autograd模块实现了损失函数对神经网络模型的权值和偏差的偏导数。 在神经网络模型中运行反向传播时,当模型的参数发生变化时,变量被专门设计用来保存更改的值。 变量类型只是张量的一个包装。 它有三个属性:data、grad和function。
import torch
x = torch.ones(2, 2, requires_grad=True)
print(x)
# tensor([[1., 1.], [1., 1.]], requires_grad=True)
a,b=12,23
x1 = torch.randn(a,b,requires_grad=True)
x2 = torch.randn(a, b, requires_grad=True)
x3 = torch.randn(a, b, requires_grad=True)
c = x1 * x2
d = a + x3
e = torch.sum(d)
e.backward()
print(e)
# tensor(3288.7356, grad_fn=)
基本统计
我们如何从一个PyTorch张量计算基本统计信息,如平均值、中值、众数等等?
使用PyTorch计算基本统计信息使用户能够应用概率分布和统计测试从数据中进行推断。虽然Torch的功能类似于Numpy,但Torch的功能具有GPU加速。让我们看看创建基本统计信息的函数。
import torch
print(torch.mean(torch.tensor([10., 10., 34., 45, 65, 67, 87, 89])))
# tensor(50.8750)
d = torch.randn(4,5)
print(d)
# tensor([[ 0.1129, -0.2895, -2.0866, -0.1485, -0.4669],
# [ 0.5108, 1.0097, 1.3574, -0.5415, -1.0887],
# [-0.0271, 0.0105, 0.7910, -1.3944, -1.0329],
# [-0.4061, 0.8181, 0.4903, -0.5656, 1.1365]])
print(torch.mean(d, dim=0))
# tensor([ 0.0476, 0.3872, 0.1380, -0.6625, -0.3630])
print(torch.mean(d, dim=1))
# tensor([-0.5757, 0.2495, -0.3306, 0.2946])
print(torch.median(d,dim=0))
# torch.return_types.median(
# values=tensor([-0.0271, 0.0105, 0.4903, -0.5656, -1.0329]),
# indices=tensor([2, 2, 3, 3, 2]))
print(torch.median(d,dim=1))
# torch.return_types.median(
# values=tensor([-0.2895, 0.5108, -0.0271, 0.4903]),
# indices=tensor([1, 0, 0, 2]))
print(torch.mode(d))
# torch.return_types.mode(
# values=tensor([-2.0866, -1.0887, -1.3944, -0.5656]),
# indices=tensor([2, 4, 3, 3]))
print(torch.mode(d, dim=0))
# torch.return_types.mode(
# values=tensor([-0.4061, -0.2895, -2.0866, -1.3944, -1.0887]),
# indices=tensor([3, 0, 0, 2, 1]))
print(torch.mode(d,dim=1))
# torch.return_types.mode(
# values=tensor([-2.0866, -1.0887, -1.3944, -0.5656]),
# indices=tensor([2, 4, 3, 3]))
标准差表示对集中趋势测度的偏差,表示数据/变量的一致性。它显示了数据是否有足够的波动。
import torch
d = torch.randn(4,5)
print(torch.std(d))
# tensor(0.9158)
print(torch.std(d,dim=0))
# tensor([0.6752, 0.9765, 1.1274, 0.6373, 0.9756])
print(torch.std(d,dim=1))
# tensor([1.0976, 0.7192, 1.1809, 0.8103])
print(torch.var(d))
# tensor(0.8387)
print(torch.var(d,dim=0))
# tensor([0.4558, 0.9535, 1.2710, 0.4061, 0.9518])
print(torch.var(d,dim=1))
# tensor([1.0976, 0.7192, 1.1809, 0.8103])
梯度计算
如何计算张量的梯度?
我们将考虑一个样本datase0074,其中有两个变量(x和y)。给定初始权值后,能否计算出每次迭代后的梯度值?让我们看一下这个例子。
import torch
def forward(x):
return x * w
x_data = [11.0, 22.0, 33.0]
y_data = [21.0, 14.0, 64.0]
w = torch.Tensor([1.0], requires_grad=True)
# 训练之前
print("Predict (before training)", 4, forward(4).data[0])
# Predict (before training) 4 tensor(4.)
print("Predict (before training)", 4, forward(4).data)
# Predict (before training) 4 tensor([4.])
print("Predict (before training)", 4, forward(4).detach().numpy()[0])
# Predict (before training) 4 4.0
print("Predict (before training)", 4, forward(4).detach().cpu().numpy()[0])
# Predict (before training) 4 4.0
# 使用前向传播
def forward(x):
return x*w;
# 定义损失函数
def loss(x,y):
y_pred=forward(x)
return (y_pred-y) * (y_pred-y)
# 训练
for epoch in range(3):
for x_val, y_val in zip(x_data, y_data):
l = loss(x_val, y_val)
l.backward()
print("\tgrad:",x_val,y_val,w.grad.data[0])
w.data = w.data - 0.01 * w.grad.data
# 更新权重后手动设置梯度为0
w.grad.data.zero_()
print("progress:", epoch, l.data[0])
# grad: 11.0 21.0 tensor(-220.)
# grad: 22.0 14.0 tensor(2481.6001)
# grad: 33.0 64.0 tensor(-51303.6484)
# progress: 0 tensor(604238.8125)
# grad: 11.0 21.0 tensor(118461.7578)
# grad: 22.0 14.0 tensor(-671630.6875)
# grad: 33.0 64.0 tensor(13114108.)
# progress: 1 tensor(3.9481e+10)
# grad: 11.0 21.0 tensor(-30279010.)
# grad: 22.0 14.0 tensor(1.7199e+08)
# grad: 33.0 64.0 tensor(-3.3589e+09)
# progress: 2 tensor(2.5900e+15)
# 训练后
print("predict (after training)", 4, forward(4).data[0])
# predict (after training) 4 tensor(3.6188e+22)
下面的程序演示了如何使用张量上的变量法从损失函数计算梯度。
import torch
a = torch.tensor([5])
weights=[torch.tensor([i], requires_grad=True, dtype=torch.float) for i in (12, 53, 91, 73)]
w1, w2, w3, w4 = weights
b = w1 * a
c = w2 * a
d = w3 * b + w4 * c
Loss = (10-d)
Loss.backward()
for index, weight in enumerate(weights, start=1):
gradient, *_ = weight.grad.data
print(f"Gradient of w{index} w.r.t to Loss: {gradient}")
# Gradient of w1 w.r.t to Loss: -455.0
# Gradient of w2 w.r.t to Loss: -365.0
# Gradient of w3 w.r.t to Loss: -60.0
# Gradient of w4 w.r.t to Loss: -265.0
张量操作
我们如何计算或执行基于变量的操作,如矩阵乘法?
张量包含在变量中,变量有三个属性:grad、volatile和gradient。
让我们创建一个变量并提取变量的属性。在权重更新过程中需要梯度计算。利用mm模块,我们可以进行矩阵乘法运算。
import torch
x = torch.randn(4,4).uniform_(-4,5)
y = torch.randn(4,4).uniform_(-3,2)
# 矩阵相乘
z = torch.mm(x,y)
print(z.size())
# torch.Size([4, 4])
# 下面的程序显示了该变量的属性
print(z)
# tensor([[ 4.6945, -7.5326, 5.9057, 13.6035],
# [-1.2912, -6.2970, -7.0016, 13.6684],
# [-9.2938, 3.0660, -8.8103, 0.9369],
# [ 0.2251, -0.6914, 7.2633, 4.1040]])
print("Requires Gradient: %s"%(z.requires_grad))
print("Volatile : %s " % (z.volatile))
print("Gradient : %s " % (z.grad))
print(z.data)
# Requires Gradient: False
# UserWarning: volatile was removed (Variable.volatile is always False)
# Volatile : False
# Gradient : None
# tensor([[ 4.6945, -7.5326, 5.9057, 13.6035],
# [-1.2912, -6.2970, -7.0016, 13.6684],
# [-9.2938, 3.0660, -8.8103, 0.9369],
# [ 0.2251, -0.6914, 7.2633, 4.1040]])
mat1 = torch.randn(4,4).uniform_(0,1)
print(mat1)
# tensor([[0.5896, 0.9198, 0.0780, 0.9008],
# [0.4366, 0.3875, 0.4819, 0.7261],
# [0.7626, 0.8824, 0.3126, 0.0613],
# [0.7845, 0.7780, 0.4653, 0.8141]])
mat2 = torch.randn(5,4).uniform_(0,1)
print(mat1)
# tensor([[0.5896, 0.9198, 0.0780, 0.9008],
# [0.4366, 0.3875, 0.4819, 0.7261],
# [0.7626, 0.8824, 0.3126, 0.0613],
# [0.7845, 0.7780, 0.4653, 0.8141]])
vec1 = torch.randn(4).uniform_(0,1)
print(vec1)
# tensor([0.4229, 0.3091, 0.6569, 0.1946])
print(mat1 + 10.5)
# tensor([[11.0896, 11.4198, 10.5780, 11.4008],
# [10.9366, 10.8875, 10.9819, 11.2261],
# [11.2626, 11.3824, 10.8126, 10.5613],
# [11.2845, 11.2780, 10.9653, 11.3141]])
print(mat2 - 0.20)
# tensor([[ 0.6409, 0.6838, 0.0247, 0.1415],
# [ 0.0827, 0.2611, 0.4746, -0.0768],
# [ 0.4831, 0.0355, 0.5180, 0.6005],
# [ 0.5719, -0.1914, 0.0744, 0.5680],
# [ 0.4381, -0.1413, 0.7248, 0.0604]])
print(mat1 + vec1)
# tensor([[1.0124, 1.2289, 0.7349, 1.0955],
# [0.8595, 0.6966, 1.1388, 0.9208],
# [1.1855, 1.1915, 0.9694, 0.2560],
# [1.2074, 1.0871, 1.1221, 1.0087]])
print(mat2 + vec1)
# tensor([[1.2638, 1.1929, 0.8815, 0.5362],
# [0.7056, 0.7702, 1.3315, 0.3178],
# [1.1060, 0.5445, 1.3749, 0.9952],
# [1.1948, 0.3177, 0.9313, 0.9626],
# [1.0610, 0.3678, 1.5817, 0.4550]])
分布
统计分布知识对于使用PyTorch进行基于神经网络的操作的权值归一化、权值初始化和梯度计算至关重要。我们如何知道使用哪个分布以及何时使用它们?
每个统计分布遵循预先建立的数学公式。我们将使用最常用的统计分布。
伯努利分布是二项分布的一种特殊情况,它的试验次数可以大于一次;但在伯努利分布中,实验次数还是1。它是一个随机变量的离散概率分布,当有事件成功的概率时取值为1,当有事件失败的概率时取值为0。一个完美的例子是抛硬币,1是正面,0是反面。让我们看看程序。
import torch
from torch.distributions.bernoulli import Bernoulli
dist = Bernoulli(torch.tensor([0.3, 0.6, 0.9]))
print(dist.sample())
# tensor([0., 1., 1.])
beta分布是一组定义在0和1范围内的连续随机变量。这个分布通常用于
贝叶斯推理分析。
from torch.distributions.beta import Beta
dist = Beta(torch.tensor([0.5]), torch.tensor([0.5]))
print(dist)
# Beta()
print(dist.sample())
# tensor([0.0261])
二项分布适用于结果为二次且实验是重复的情况。它属于离散概率分布族,其中成功概率定义为1,失败概率为0。二项分布被用来模拟多次试验中成功事件的数量。
from torch.distributions.binomial import Binomial
dist=Binomial(100, torch.tensor([0, 0.2, 0.8, 1]))
print(dist.sample())
# tensor([ 0., 22., 82., 100.])
在概率和统计中,分类分布可以定义为广义伯努利分布,这是一种离散的概率分布,它解释了任意随机变量的可能结果,它可能出现在一个可能的类别中,每个类别的概率都在张量中指定。
from torch.distributions.categorical import Categorical
dist = Categorical(torch.tensor([0.2, 0.2, 0.2, 0.2, 0.2]))
print(dist)
print(dist.sample())
# Categorical(probs: torch.Size([5]))
# tensor(4)
拉普拉斯分布是一个连续的概率分布函数,也被称为双指数分布。在语音识别系统中使用拉普拉斯分布来理解先验概率。它在确定先验概率的贝叶斯回归中也很有用。
from torch.distributions.laplace import Laplace
dist=Laplace(torch.tensor([10.0]), torch.tensor([0.990]))
print(dist)
print(dist.sample())
# Laplace(loc: tensor([10.]), scale: tensor([0.9900]))
# tensor([11.1710])
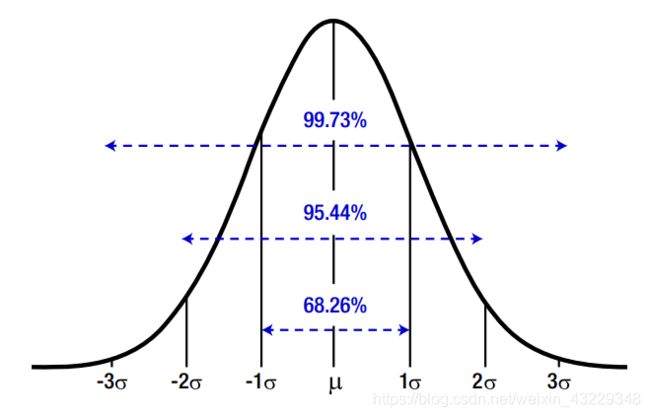
因为中心极限定理的性质,正态分布非常有用。它由均值和标准差定义。如果我们知道分布的均值和标准差,我们就可以估计事件的概率。
from torch.distributions.normal import Normal
dist=Normal(torch.tensor([100.0]), torch.tensor([10.]))
print(dist)
print(dist.sample())
# Normal(loc: tensor([100.]), scale: tensor([10.]))
# tensor([113.5797])
总结
本章讨论了抽样分布和从分布中生成随机数。神经网络是基于张量运算的主要研究方向。任何类型的机器学习或深度学习模型的实现都需要梯度计算、更新权值、计算损失以及不断更新损失。
本章还讨论了PyTorch支持的统计分布以及可以应用分布的情景。
下一章详细讨论深度学习模型。这些深度学习模型包括卷积神经网络、循环神经网络、深度神经网络和自动编码器模型。