用遗传算法解决VRP问题
项目地址
车辆路径问题 (Vehicle Routing Problem,以下简称VRP问题)最早由Dantzig和Ramser于1959年首次提出,是运筹学中一个经典问题。VRP问题主要研究物流配送中的车辆路径规划问题,是当今物流行业中的基础问题。
VRP问题的主要研究对象是以下问题:
有一个配送中心,每天需要向若干配送点配送货物,配送中心有若干辆车可用于配送。已知配送中心和各配送点的位置,请问如何设计配送方案才能让配送效率尽可能高?
该问题是一类物流配送优化问题的典型代表。对以上问题进行不同条件的约束,并设定不同的最优化目标,就得到了不同种类的VRP问题。VRP问题一共有十几种类型,每种类型的求解算法都大不相同。
VRP问题属于NPC问题,目前没有多项式时间复杂度的求解算法。求解VRP问题是一项十分具有挑战性的工作。
拓展资料:
车辆路径问题(MBA智库)
车辆路径问题详解(百度文库)
物流配送问题(百度文库)
什么是P问题、NP问题和NPC问题(Matrix67)
VRP问题简介
根据赛题要求,我们研究的VRP问题模型如下所示。
如图,某地有一配送中心,负责将货物配送到指定的各个配送点。每个配送点有一定的货物需求量,用货物重量表示。配送中心有若干辆车,每辆车有一定的载重量和里程限制,车的载重和行驶里程不可超过指定的值。一辆车可负责一个或多个点的配送任务,且每个配送点只被服务一次。在某一时刻,所有负责配送的车同时从配送中心出发,分别完成各自的配送任务后,再回到配送中心。
根据以上条件,设计一个最优配送方案。对于每个方案,应给出每辆车负责的配送点及其先后顺序。上图显示了一个三辆车的配送方案。
为衡量方案之间的优劣,我们给出如下三个指标:
- 配送总时间 t t t:从配送开始到最后一辆车返回物流中心所经历的时间
- 车辆总里程 s s s:所有配送车辆的里程之和
- 车辆总数 n n n:用于配送的车辆数量
在实际应用中,我们为这三个指标分别分配一个权重 w t w_t wt、 w s w_s ws 和 w n w_n wn,然后用如下公式作为每个方案的得分:
s c o r e = − ( w t ⋅ t + w s ⋅ s + w n ⋅ n ) score=-(w_t \cdot t + w_s \cdot s + w_n \cdot n) score=−(wt⋅t+ws⋅s+wn⋅n)
得分越高,说明方案越优。
严格地说,我们要解决的问题是带时间约束和载重约束的VRP问题。这属于VRP问题中较为简单的一种类型。下文提到的“VRP问题”都是指这种类型的VRP问题。
用穷举法求解VRP问题
为了直观地体会VRP问题的难度,这里介绍一下如何用穷举法求解VRP问题。
穷举法的基本思路是:遍历所有可能的配送方案,从中选取得分最高的方案(得分计算方法见上一节)。理论上,穷举法可以找到问题的最优解。
为便于叙述,我们将所有配送点编号为 1 1 1 到 n n n ,将所有车辆编号为 1 1 1 到 m m m 。
配送方案的表示
我们用一个长度为 n + m − 1 n+m-1 n+m−1 的整数数组表示(编码)一个配送方案。该数组包含 1 1 1 到 n n n 的全排列和 m − 1 m-1 m−1 个 0 0 0 。这 m − 1 m-1 m−1 个 0 0 0 将 1 1 1 到 n n n 的全排列分成了 m m m 段,从左到右第 i i i 段表示第 i i i 辆车的配送路线(具体含义请见下面例子)。注意:可能有的 0 0 0 是相邻的,或者位于数组两端,这表示某些编号的车不参与配送。
例1:
2 1 3 0 9 4 7 6 0 8 5 2\quad1\quad3\quad0\quad9\quad4\quad7\quad6\quad0\quad8\quad5 21309476085上面的方案表明:第一辆车服务编号为 2 , 1 , 3 2,1,3 2,1,3 的配送点,且顺序为 2 → 1 → 3 2\rightarrow 1\rightarrow 3 2→1→3 ;第二辆车服务编号为 9 , 4 , 7 , 6 9,4,7,6 9,4,7,6 的配送点,且顺序为 9 → 4 → 7 → 6 9\rightarrow 4\rightarrow 7\rightarrow 6 9→4→7→6 ,依此类推。
例2:
6 8 7 9 0 5 4 1 2 3 0 6\quad8\quad7\quad9\quad0\quad5\quad4\quad1\quad2\quad3\quad0 68790541230该方案只用到了两辆车,第一辆车服务 6 , 8 , 7 , 9 6,8,7,9 6,8,7,9 号配送点,第二辆车服务 5 , 4 , 1 , 2 , 3 5,4,1,2,3 5,4,1,2,3 号配送点,第三辆车不参与配送。
例3:
5 4 6 8 0 0 3 1 2 7 9 5\quad4\quad6\quad8\quad0\quad0\quad3\quad1\quad2\quad7\quad9 54680031279
该方案只用到了两辆车,第一辆车服务 5 , 4 , 6 , 8 5,4,6,8 5,4,6,8 号配送点,第二辆车不参与配送,第三辆车服务 3 , 1 , 2 , 7 , 9 3,1,2,7,9 3,1,2,7,9 号配送点。
显然,这种编码方式可以表示所有可能的配送方案。
注意,由于载重量和里程约束,以上方法产生的一些方案是不合法的,这里假定程序会在运行时判断方案的合法性。
方案总数的计算
理论上,有了以上表示配送方案的方法,我们就可以写出穷举法的求解程序了。关键步骤如下:
- 遍历 1 1 1 - n n n 这 n n n 个数和 m − 1 m-1 m−1 个 0 0 0 组成的序列的全排列。
- 计算出每种排列对应的方案的得分,从而得到得分最高的方案。
事实上,我们不会写这个程序,因为即使对于 n = 20 n=20 n=20, m = 5 m=5 m=5 这样的小规模数据,程序要枚举的方案数也是天文数字,以下是具体的计算。
n + m − 1 n+m-1 n+m−1 个数的排列共有 ( n + m − 1 ) ! (n+m-1)! (n+m−1)! 种,其中有 m − 1 m-1 m−1 个重复的 0 0 0 ,因此所有可能的方案数如下:
( n + m − 1 ) ! ( m − 1 ) ! \frac{(n+m-1)!}{(m-1)!} (m−1)!(n+m−1)!
当 n = 20 n=20 n=20, m = 5 m=5 m=5 时,方案数为:
( 20 + 5 − 1 ) ! ( 5 − 1 ) ! = 25852016738884976640000 \frac{(20+5-1)!}{(5-1)!}=25852016738884976640000 (5−1)!(20+5−1)!=25852016738884976640000
假设我们的计算机一秒钟可以遍历 1 0 9 10^9 109 种方案(根据普通家用计算机的运行速度),那么要遍历完以上所有的方案需要的时间为:
25852016738884976640000 1 0 9 ⋅ 60 ⋅ 60 ⋅ 24 ⋅ 365 = 819762 ( 年 ) \frac{25852016738884976640000}{10^{9}\cdot60\cdot60\cdot24\cdot365}=819762(年) 109⋅60⋅60⋅24⋅36525852016738884976640000=819762(年)
也就是说,即使 n n n 取很小的数值,穷举法的运行时间也是不可接受的。这种现象称为组合爆炸。
其它穷举法
除了以上方法,VRP问题的穷举法还有如下几种:分支界定法、割平面法、网络流算法、动态规划法等。这些算法对传统的穷举法进行了一些效率上的优化,但还是存在组合爆炸问题。
拓展资料:
车辆路径问题详解(百度文库)
物流配送问题(百度文库)
启发式算法简介
由于组合爆炸现象,即使在问题规模较小时,VRP问题的解空间也十分庞大(解空间就是所有可能方案的集合)。由于穷举法必须要枚举整个解空间才能得出结果,因此利用穷举法来求解VRP问题是十分低效的,即使能够在效率上进行一些改进,也远远达不到当前计算机运算速度的数量级。于是,人们开始思考,是否存在一种算法,能够枚举部分解空间就能得到问题的解呢?显然,如果这种算法存在,那么它不能保证找到最优解。因此,人们将重心转移到如何寻找较优解上。于是,出现了一系列启发式算法。
启发式算法
启发式算法,是一种不同于穷举法的搜索算法。它的主要特点如下:
- 启发式算法不会枚举所有的方案,而是仅仅考察少量的方案就得出结果
- 启发式算法不保证找到最优解,很多时候只能找到较优解
启发式算法在运行时,会根据前面枚举的结果,采用某种策略来选择下一次枚举的方案,使得下一次方案尽量更接近问题的最优解,并在迭代一定次数后停止。由于启发式算法不用枚举整个解空间,因此效率比较高,但是启发式算法采用的搜索策略会对结果的质量产生很大的影响,而搜索策略的制定也主要依靠人的经验。
启发式算法之所以能工作,是由于以下原理:
上一次的搜索结果能为下一次的搜索方向提供有用的信息。
几乎所有启发式算法都使用了以上原理来制定搜索策略。下面介绍遗传算法的时候,将对这个原理有更深入的了解。
VRP问题中的启发式求解算法
目前有许多种启发式算法可以解决VRP问题:C-W节约法、最邻近法、最近插入法、粒子群算法、模拟退火算法、遗传算法……等等。
这些算法的特点各不相同,求解质量也有着很大的差别。效果相对来说较好的算法有粒子群算法、模拟退火算法和遗传算法。
由于遗传算法原理和实现都相对比较简单,效果也比较好,因此我们主要研究用遗传算法求解VRP问题。
拓展资料:
车辆路径问题详解(百度文库)
物流配送问题(百度文库)
遗传算法简介
遗传算法(Genetic Algorithm,GA)是一种通过模拟生物进化过程来求解最优化问题的启发式算法。遗传算法的主要理论依据是达尔文的自然选择学说。遗传算法是一种十分通用的搜索算法,可以用来求解多种问题,且效果还不错。
基本概念
首先介绍遗传算法中的几个概念:
- 基因:一个单独的、不可分割的遗传因子。每个基因都决定着个体某一方面的性状。
- 染色体:一组不同基因的线性排列。每条染色体上有多个不同的基因。
- 个体:一个独立的生物体。每个个体都有一条染色体。事实上,很多时候可以用染色体来代表个体。
- 种群:个体的集合。种群中的个体一般具有相同长度的染色体,但是染色体上的基因可能不同。
- 适应度:个体对环境的适应程度。适应度越高,个体对当前环境的适应能力越好,存活的概率也越大。
- 繁殖:旧个体产生新个体的过程。繁殖过程一般包含两个个体的染色体的变异、重组操作(下面会介绍这两种操作)。新个体仍然属于父代种群。
- 选择:随机选择一定数量的种群中的个体,只有被选择的个体保留到下一代,满足适应度越高的个体被选择的概率越大。
- 进化:一个种群经过一轮选择、繁殖操作后,会变成一个新的种群,新种群的个体数量与原种群相同。这个过程被称为“进化了一代”。
自然选择学说
自然选择学说是由达尔文提出的关于生物进化机理的一种学说,讲述的是“物竞天择,适者生存”的自然原理,生物体通过自然选择、基因突变和遗传等规律进化出适应环境变化的优良品种。在环境压力下,适应度高的个体得以保存下来,从而影响整个种群的进化方向。
生物的进化,本质上是基因的优胜劣汰过程。在每轮自然选择中,优良的基因片段有更大的几率保留下来,而劣势基因片段则大概率减少或消失。久而久之,优良基因会在种群中占据主导地位,而劣势基因会逐渐销声匿迹。
自然选择最重要的阶段是遗传变异,这个阶段是产生种群多样性的唯一阶段。遗传变异一般是通过基因突变和基因重组实现的。
- 基因突变:某基因随机变成了另一个完全不同的基因。基因突变可以产生新的基因,新基因表达的性状可能是有益的,也可能是有害的(大多数情况下是有害的)。基因突变是产生种群多样性的主要原因。基因突变发生的概率很低。
- 基因重组:两条染色体的部分片段发生了随机交换。基因重组不会产生新的基因,但是可能将父代的一些优良基因片段集中到子代基因上(当然,也有可能将父代不好的基因片段集中到子代基因上)。基因重组发生的概率也很低,但是比基因突变的概率高。
遗传算法基本流程
遗传算法忠实地复原了生物进化的过程。以下是遗传算法的基本流程:
该流程适用于所有遗传算法,但是对于具体问题应用遗传算法时,需要根据具体问题设计算法中各种遗传操作。
拓展资料:
遗传算法:内存中的进化(科学松鼠会)
有史以来最容易理解的遗传算法(知乎)
用遗传算法求解VRP问题
遗传算法求解的关键是设计个体的存储结构和各种遗传操作的实现。这些细节不仅决定程序实现的难度,也影响着算法最终的执行效果。
为便于叙述,我们将所有配送点编号为 1 1 1 到 n n n ,将所有车辆编号为 1 1 1 到 m m m 。
个体的编码
为方便起见,个体的编码采用与穷举法中相同的编码方案。这种方案简单直观,没有冗余信息,而且可以简化接下来的变异操作,提高程序的运行效率。
个体的生成
利用如下算法随机生成一个个体:
- 随机生成 1 1 1 到 n n n 的全排列。
- 在排列中随机插入 m − 1 m-1 m−1 个 0 0 0 。
注意:由于载重量和里程的约束,以上算法生成的个体可能是不合法的,因此在第二步分割时需要根据当前车辆的里程和载重进行合理划分,以保证所有生成的个体都是合法的。
初始种群的生成
利用以上算法随机生成 1000 1000 1000 个个体作为初始种群。
适应度计算
个体的适应度根据以下公式计算:
f i t n e s s = s c o r e = − ( w t ⋅ t + w s ⋅ s + w n ⋅ n ) fitness=score=-(w_t \cdot t + w_s \cdot s + w_n \cdot n) fitness=score=−(wt⋅t+ws⋅s+wn⋅n)
其中 s c o r e score score 为问题分析中介绍过的得分公式。
选择操作
按照如下步骤对种群进行选择:
- 对种群中的所有个体按照适应度从大到小排序。
- 选择前 50 % 50\% 50% 的个体(即适应度较大的 50 % 50\% 50% 个体)保留到下一代。
执行选择操作后,种群中的个体数减少为原来的一半,后面会通过繁殖操作使种群大小恢复为原来的水平。
变异操作
按照如下步骤对个体进行变异:
- 随机选定个体数组中的两个元素。
- 交换两个元素的值。
- 若变异后的个体不合法,则变异失败,撤销变异操作(即保持个体不变)。
例:
2 1 3 0 9 4 7 6 0 8 5 2\quad1\quad3\quad0\quad9\quad4\quad7\quad6\quad0\quad8\quad5 21309476085
该个体变异后可能产生的新个体如下:
2 1 3 0 7 4 9 6 0 8 5 2\quad1\quad3\quad0\quad7\quad4\quad9\quad6\quad0\quad8\quad5 21307496085
其中9和7交换了位置,改变了第二辆车配送的顺序。还可能产生如下的变异:
2 4 3 7 9 1 0 6 0 8 5 2\quad4\quad3\quad7\quad9\quad1\quad0\quad6\quad0\quad8\quad5 24379106085
这次变异交换了0的位置,产生了一个新划分。
显然,若个体能成功变异,则经过变异后的个体还是合法的。这种变异算法能够很好地保留父代的大部分特征,同时也有一定的机率产生较大的改变(如上例中的第二种变异情况),可以大大增强种群多样性,提高算法搜索的效果。
交叉操作
如果用传统的交叉算法(即随机交换两条染色体的片段)对个体进行交叉操作,则交叉后产生的新个体不一定是合法的,需要进行调整。为简单起见,这里不对个体进行交叉操作,仅仅通过变异操作产生新个体。
繁殖操作
选择操作后,种群大小变为原来的一半。每次在留下的个体中随机选取一个进行变异操作(若变异失败,则重新选择一个个体),并将产生的新个体插入到种群中,直到种群恢复原来的大小。
算法结束条件
程序会记录每次进化过程中个体的最大适应度。若最大适应度持续 1000 1000 1000 代都无变化,则结束算法,并输出最大适应度对应的方案。
算法执行效果展示
利用以上遗传算法实现的程序能够在较短时间内求解一定规模的VRP问题,且求解质量还不错。以下给出不同规模的VRP问题的求解结果和相关数据。
地图中的红点P表示配送中心,蓝点表示配送点,蓝点旁边的数字表示需求量。
下面是各个问题的相关参数:
| 问题规模 | 车辆总数 | 载重约束 | 里程约束 | 权重( w t : w s : w n w_t:w_s:w_n wt:ws:wn) |
|---|---|---|---|---|
| 10个配送点 | 5 5 5 | 全部为5 | 20 20 20 | 1 : 1 : 1 1:1:1 1:1:1 |
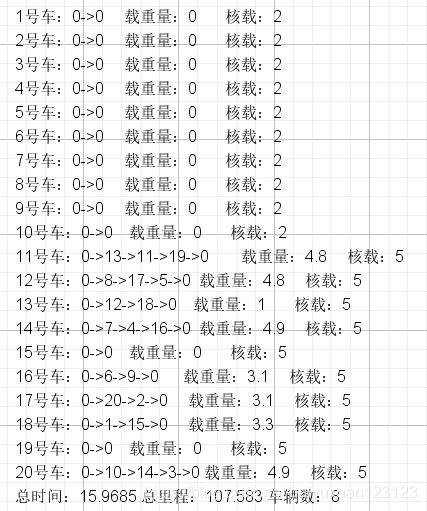
| 20个配送点 | 20 20 20 | 10辆为2,10辆为5 | 20 20 20 | 1 : 1 : 10 1:1:10 1:1:10 |
| 30个配送点 | 20 20 20 | 10辆为2,10辆为5 | 20 20 20 | 1 : 1 : 2 1:1:2 1:1:2 |
| 40个配送点 | 20 20 20 | 全部为5 | 20 20 20 | 1 : 10 : 1 1:10:1 1:10:1 |
| 50个配送点 | 20 20 20 | 全部为5 | 20 20 20 | 10 : 1 : 1 10:1:1 10:1:1 |
注:数据中的时间、重量和里程经过单位换算,不代表实际大小,只表示相对大小。
10个配送点
20个配送点
30个配送点
40个配送点
50个配送点
项目地址