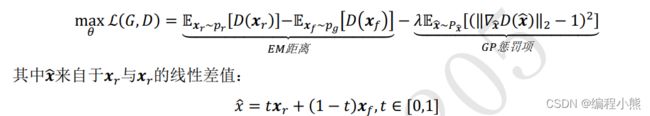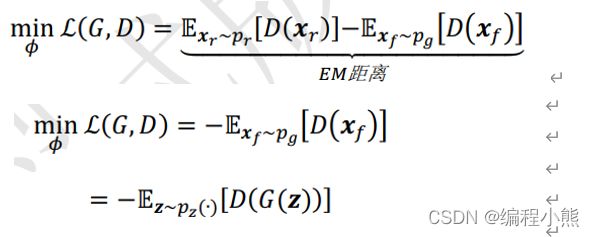生成对抗网络(GAN)

博弈学习引出：用一个漫画家的成长轨迹来形象介绍生成对抗网络的思想：一对双胞胎兄弟， 分别称为老二G和老大 D， G 学习如何绘制漫画， D 学习如何鉴赏画作。在年幼时代G,D，尚且只学会了如何使用画笔和纸张， G 绘制了一张不明所以的画作，如图(a)所示，由于此时 D 鉴别能力不高， 觉得 G 的作品还行，但是人物主体不够鲜明。 在D 的指引和鼓励下， G 开始尝试学习如何绘制主体轮廓和使用简单的色彩搭配。

随之G 提升了绘画的基本功， D 也过分析名作和初学者 G 的作品， 初步掌握了鉴别作品的能力。 此时 D 觉得 G 的作品人物主体有了，如图 (b)， 但是色彩的运用还不够成熟。

数年后， G 的绘画基本功已经很扎实了，可以轻松绘制出主体鲜明、颜色搭配合适和逼真度较高的画作， 如图 (c)， 但是 D 同样通过观察 G 和其它名作的差别， 提升了画作鉴别能力， 觉得 G 的画作技艺已经趋于成熟，但是对生活的观察尚且不够，作品没有传达神情且部分细节不够完美。

又过了数年， G 的绘画功力达到了炉火纯青的地步，绘制的作品细节完美、 风格迥异、 惟妙惟肖，宛如大师级水准，如图(d)，即便此时的D 鉴别功力也相当出色， 亦很难将 G 和其他大师级的作品区分开来
 

一、GAN原理

画家的成长历程是生活中普遍存在的学习过程，通过双方的博弈学习，相互提高，最终达到一个平衡点。GAN 网络借鉴了博弈学习的思想，分别设立了两个子网络：负责生成样本的生成器 G 和负责鉴别真伪的鉴别器 D。生成器 G是画家，鉴别器 D鉴别家。 鉴别器 D通过观察真实的样本和生成器 G 产生的样本之间的区别， 学会如何鉴别真假，其中真实的样本为真，生成器 G 产生的样本为假。生成器 G 同样也在学习， 它希望产生的样本能够获得鉴别器 D 的认可，即在鉴别器 D 中鉴别为真，因此生成器 G 通过优化自身的参数，尝试使得自己产生的样本在鉴别器 D 中判别为真

生成器 G 和鉴别器 D 相互博弈，共同提升，直至达到平衡点。使生成器 G 生成的样本非常逼真， 鉴别器 D 真假难分。

1.网络结构

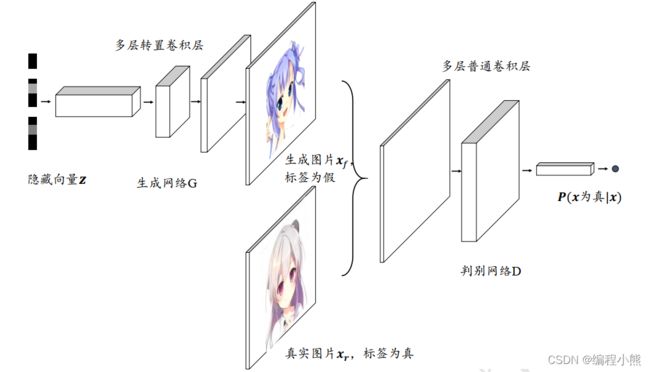
生成对抗网络包含了两个子网络： 生成网络(Generator， 简称 G)和判别网络(Discriminator， 简称 D)， 其中生成网络 G 负责学习样本的真实分布，判别网络 D 负责将生成网络采样的样本与真实样本区分开来
 

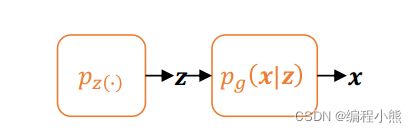
生成网络G()

生成网络 G 和自编码器的 Decoder 功能类似， 从先验分布中采样隐藏变量，通过生成网络 G 参数化的分布， 获得生成样本， 其中隐藏变量的先验分布可以假设为某中已知的分布，比如多元均匀分布。

 

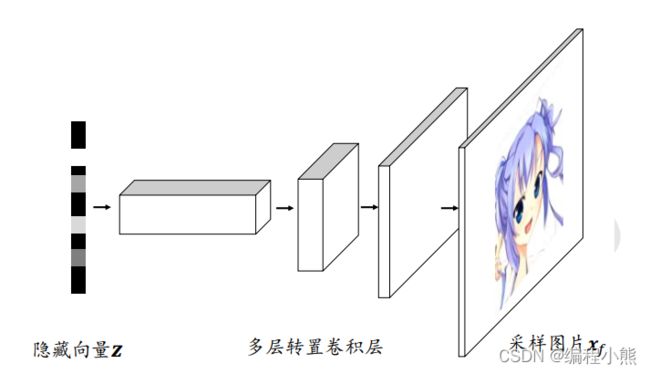
 可以用深度神经网络来参数化，从均匀分布中采样出隐藏变量， 经过多层转置卷积层网络参数化的分布中采样出样本。 从输入输出层面来看，生成器 G 的功能是将隐向量通过神经网络转换为样本向量，下标代表假样本(Fake samples)。

 

 补充：先验分布：是概率分布的一种，与“后验分布”相对。与试验结果无关，或与随机抽样无关，反映在进行统计试验之前根据其他有关参数θ的知识而得到的分布。在进行观察以获得样本之前，人们对θ也会有一些知识。因为是在试验观察之前，故称之为先验知识。因此，应该把θ看作是随机变量。θ的分布函数记为H（θ），θ的密度函数记为h(θ)，分别称为先验分布函数和先验密度数，两者合称为先验分布

 判别网络D()

判别网络和普通的二分类网络功能类似，它接受输入样本的数据集，包含了采样自真实数据分布的样本，也包含了采样自生成网络的假样本， 和共同组成了判别网络的训练数据集。判别网络输出为属于真实样本的概率(为真|)，把所有真实样本的标签标注为真(1)；所有生成网络产生的样本标注为假(0)， 通过最小化判别网络 D 的预测值与标签之间的误差来优化判别网络参数

 转置卷积(Transposed Convolution)

转置卷积(Transposed Convolution或 Fractionally Strided Convolution)，也称反卷积(Deconvolution）， 实际上反卷积在数学上定义为卷积的逆过程，但转置卷积并不能恢复出原卷积的输入，因此称为反卷积并不妥当。通过在输入之间填充大量的 padding 来实现输出高宽大于输入高宽的效果，从而实现向上采样的目的

输入为2 × 2的单通道特征图，转置卷积核为3 × 3大小，步长 = 2，填充 = 0的。首先在输入数据点之间均匀插入s-1个空白数据点，得到3 × 3的矩阵，第 2 个矩阵所示，根据填充量在3 × 3矩阵周围填充相应 - -1 = 3 -0 -1 = 2行/列，此时输入张量的高宽为 7×7 ， 如图中第 3 个矩阵所示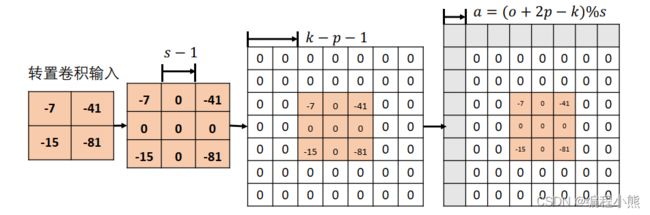

在 7×7 的输入张量上，进行3 × 3卷积核，步长′ = 1，填充 = 0的普通卷积运算(注意，此阶段的普通卷积的步长′始终为 1，与转置卷积的步长不同)， 根据普通卷积的输出计算公式， 得到输出大小为，即5x5的输出。转置卷积输出与输入关系：

在 +2 - 为 s 倍数时，满足关系： = ( -1 ) + - 2

转置卷积并不是普通卷积的逆过程，但是二者之间有一定的联系，同时转置卷积也是基于普通卷积实现的。在相同的设定下，输入经过普通卷积运算后得到 = Conv()；将送入转置卷积运后，得到′ = ConvTranspose()，其中′ ≠ ，但是′与形状相同。转置卷积与普通卷积并不是互为逆过程，不能恢复出对方的输入内容，仅能恢复出等大小的张量。
 

转置卷积的转置是指卷积核矩阵产生的稀疏矩阵′在计算过程中需要先转置，再进行矩阵相乘运算，而普通卷积并没有转置′的步骤,  这也是它被称为转置卷积的名字由来
 

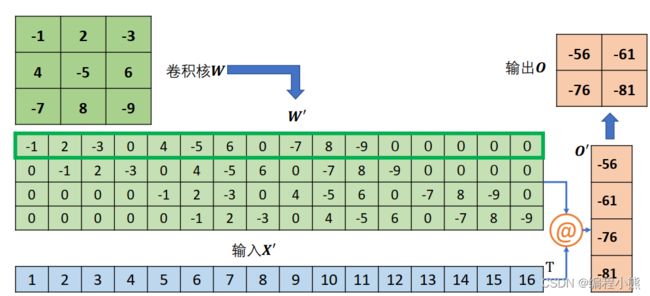
和，需要根据 strides 将卷积核在行、列方向循环移动获取参与运算的感受野的数据， 串行计算每个窗口处的“相乘累加” 值，计算效率极低。为了加速运算，在数学上可以将卷积核根据 strides 重排成稀疏矩阵′， 再通过′@′一次完成运算, 实际上， ′矩阵过于稀疏， 导致很多无用的 0 乘运算。

以 4 行 4 列的输入， 高宽为3 × 3， 步长为 1，无 padding 的卷积核的卷积运算为例，首先将打平成′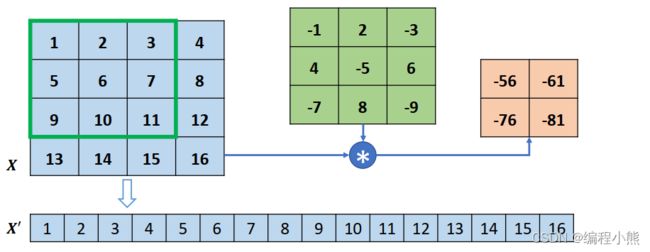

 然后将卷积核转换成稀疏矩阵′

此时通过一次矩阵相乘即可实现普通卷积运算：′ = ′@。如果给定，希望能够生成与同形状大小的张量，怎么实现呢？ 将′转置后与重排后的′完成矩阵相乘即可：′ = @'。得到的′通过 Reshape 操作变为与原来的输入尺寸一致，但是内容不同。

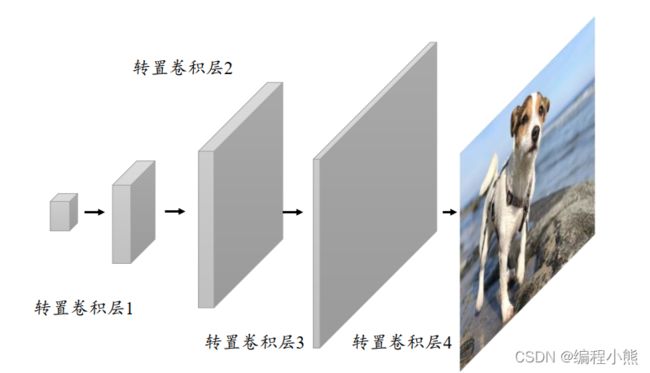
 转置卷积具有“放大特征图”的功能，在生成对抗网络、语义分割等中得到了广泛应用，如 DCGAN中的生成器通过堆叠转置卷积层实现逐层“放大”特征图
 

在 TensorFlow 中，可以通过 nn.conv2d_transpose 实现转置卷积运算。注意转置卷积的卷积核的定义格式为 [, , , ] 。转置卷积也可以和其他层一样，通过 layers.Conv2DTranspose 类创建一个转置卷积层，然后调用实例即可完成前向计算。

padding需要设置，只能设置为 VALID 或者 SAME

当设置 padding=’VALID’时，输出大小表达为： = ( - 1) +
当设置 padding=’SAME’时，输出大小表达为： = ∙
i：转置卷积输入大小 

s：strides, 步长

k:  卷积核大小

2 × 2的转置卷积输入与3 × 3的卷积核运算， strides=1， padding=’VALID’时， 输出大
小为：ℎ′ = ′ = (2 -1 ) ∙1 + 3 = 4

2 × 2的转置卷积输入与3 × 3的卷积核运算， strides=3， padding=’SAME’时，输出大小为：
ℎ′ = ′ = 2 ∙ 3 = 6

2.网络训练

对于GAN博弈学习的思想体现在它的训练方式上，由于生成器G和判别器D的优化目标不一样，所以要分开训练生成器G和判别器D。

对于判别网络 D，它的目标是能够很好地分辨出真样本与假样本。以图片生成为例， 它的目标是最小化图片的预测值和真实值之间的交叉熵损失函数： ，代表真实样本在判别网络的输出， 为判别网络的参数集， 为生成样本在判别网络的输出， 为的标签，由于真实样本标注为真，故 = 1， 为生成样本的的标签，由于生成样本标注为假，故 = 0。 CE 函数代表交叉熵损失函数CrossEntropy。

由二分类问题的交叉熵损失函数定义可知：网络 D 的优化目标是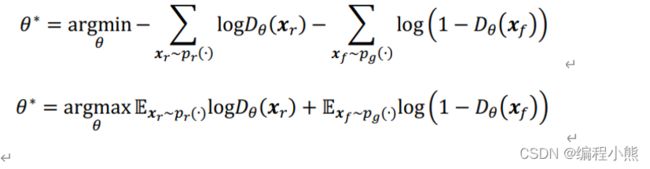

对于生成网络G()，希望 = ()能够很好地骗过判别网络 D， 假样本在判别网络的输出越接近真实的标签越好。在训练生成网络时， 希望判别网络的输出(())越逼近 1 越好， 最小化(())与 1 之间的交叉熵损失函数：

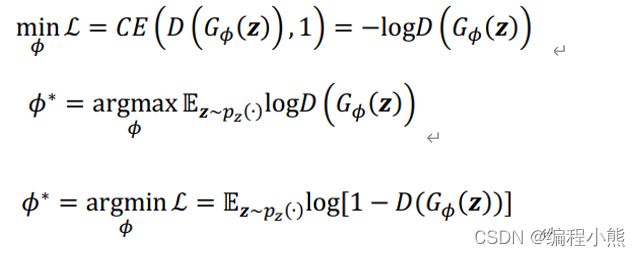
把判别网络的目标和生成网络的目标合并，写成min - max博弈形式

它的做法是去最大化D的区分度，最小化G和real数据集的数据分布。
     

生成网络 G 最终将收敛到真实分布，即： = 。此时生成的样本与真实样本来自同一分布，真假难辨，在判别器中均有相同的概率判定为真或假，即

 

 

 二、GAN类型

 

1.DCGAN

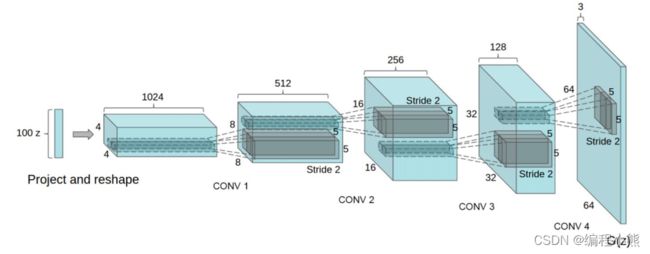
最初始的 GAN 网络主要基于全连接层实现生成器 G 和判别器 D 网络，由于图片的维度较高，网络参数量巨大，训练的效果并不优秀。 DCGAN提出了使用转置卷积层实现的生成网络，普通卷积层来实现的判别网络， 大大地降低了网络参数量，同时图片的生成效果也大幅提升
 

2.WGAN

GAN 的训练很容易出现训练不收敛和模式崩塌的现象。 WGAN从理论层面分析了原始的 GAN 使用 JS 散度存在的缺陷，并提出了可以使用 Wasserstein距离来解决这个问题。在 WGAN-GP中， 提出了通过添加梯度惩罚项， 从工程层面很好的实现了 WGAN 算法，并且实验性证实了 WGAN 训练稳定的优点

由于JS 散度导致 GAN 训练不稳定的问题，引入了一种新的分布距离度量方法： Wasserstein 距离，也叫推土机距离(Earth-Mover Distance， 简称 EM 距离)， 它表示了从一个分布变换到另一个分布的最小代价。

WGAN 的判别器 D 的训练目标为

 

WGAN 的生成器 G 的训练目标