粒子群算法改进——自适应惯性权重

适应度回顾

适应度用于评价粒子优劣，一般设置为目标函数值

众所周知

• 一个较大的惯性权重有利于全局搜索
• 一个较小的惯性权重有利于局部搜索

基本粒子群算法的粒子速度迭代公式：

v_i^d=wv_i^d-1+c₁r₁(pbest_i^d-x_i^d)+c₂r₂(gbest^d-x_i^d)

w是定值，代表粒子自身的惯性权重，但随着迭代次数的增加，问题的求解细节也会有所改变，固定值在整体求解的过程中存在不少缺陷。因而，引入变动的惯性权重，以动态适应问题的求解流程。以下是两种用自适应惯性权重求解问题的范例。

求解最小值问题

1、w_min和w_max是预设的最小与最大惯性系数，一般w_min取0.4，w_max取0.9
2、f_average^d为第d次迭代时所有粒子的平均适应度
3、f_min^d=min{f(x₁^d),f(x₂^d),…，f(x_n^d)}，即第d次迭代时所有粒子的最小适应度

• 适应度越小，说明距离最优解越近，此时更需要局部搜索
• 适应度越大，说明距离最优解越远，此时跟需要全局搜索

求解最大值问题

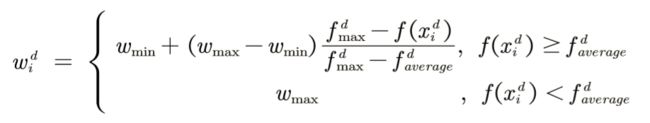
1、w_min和w_max是预设的最小与最大惯性系数，一般w_min取0.4，w_max取0.9
2、f_average^d为第d次迭代时所有粒子的平均适应度
3、f_max^d=max{f(x₁^d),f(x₂^d),…，f(x_n^d)}，即第d次迭代时所有粒子的最大适应度

• 适应度越小，说明距离最优解越近，此时更需要局部搜索
• 适应度越大，说明距离最优解越远，此时跟需要全局搜索

与基本粒子群算法相比，现在的惯性权重与迭代次数和每个粒子的适应度都有关

举个栗子

• 求解最大值问题
  假设目前有五个粒子ABCDE
  它们此刻各自的适应度分别为9，8，7，6，5
  取最小惯性权重0.4，最大惯性权重0.9
  那么，带入公式可以求得
  f_average^d=（9+8+7+6+5）/5 = 7
  f_max^d = max{9,8,7,6,5} = 9
  此刻五个粒子的惯性权重分别为：
  A: 0.4+ (0.9-0.4) (9-9)/(9-7) = 0.4
  B: 0.4+(0.9-0.4) (9-8)/(9-7) = 0.65
  C: 0.4 + (0.9-0.4) (9-7)/(9-7) = 0.9
  D: 0.9
  E: 0.9

怎么去理解这个公式呢？
因为要求解的是最大值问题（求解最大适应度），那么当粒子的适应度小于平均适应度时，表示粒子距最大值相对较远，需要扩大搜索范围来寻找最值；当粒子的适应度大于平均适应度时，表示粒子距离最大值较近，需要缩小搜索范围进行局部精确搜索。

代码实现

clear
%% 绘制函数的图形
x = -5:0.01:5;
y = 7*cos(5*x) + 4*sin(x);
figure(1)
plot(x,y,'b-')
title('y = 7*cos(5*x) + 4*sin(x)')
hold on  % 不关闭图形，继续在上面画图

%% 粒子群算法中的预设参数（参数的设置不是固定的，可以适当修改）
n = 10; % 粒子数量
narvs = 1; % 变量个数
c1 = 2;  % 每个粒子的个体学习因子
c2 = 2;  % 每个粒子的社会学习因子
w_max = 0.9;  % 最大惯性权重，通常取0.9
w_min = 0.4; % 最小惯性权重，通常取0.4
K = 50;  % 迭代的次数
vmax = 1.2; % 粒子的最大速度
x_lb = -3; % x的下界
x_ub = 3; % x的上界

%% 初始化粒子的位置和速度
x = zeros(n,narvs);
x = x_lb + (x_ub-x_lb).*rand(n,narvs)    % 随机初始化粒子所在的位置
v = -vmax + 2*vmax .* rand(n,narvs);  % 随机初始化粒子的速度

%% 计算适应度
fit = zeros(n,1);  % 初始化这n个粒子的适应度全为0
for i = 1:n  % 循环整个粒子群，计算每一个粒子的适应度
    fit(i) = Obj_fun1(x(i,:));   % 调用Obj_fun1函数来计算适应度
end
pbest = x;   % 初始化这n个粒子迄今为止找到的最佳位置（是一个n*narvs的向量）
ind = find(fit == max(fit), 1);  % 找到适应度最大的那个粒子的下标
gbest = x(ind,:);  % 定义所有粒子迄今为止找到的最佳位置（是一个1*narvs的向量）

%% 在图上标上这n个粒子的位置用于演示
h = scatter(x,fit,80,'*r');  % scatter是绘制二维散点图的函数

%% 迭代K次来更新速度与位置
fitnessbest = ones(K,1);  % 初始化每次迭代得到的最佳的适应度
for d = 1:K  % 开始迭代，一共迭代K次
    for i = 1:n   % 依次更新第i个粒子的速度与位置
        f_i = fit(i);  % 取出第i个粒子的适应度
        f_avg = sum(fit)/n;  % 计算此时适应度的平均值
        f_max = max(fit); % 计算此时适应度的最大值
        if f_i >= f_avg  
            if f_avg ~= f_max  % 如果分母为0，我们就干脆令w=w_max
                w = w_min + (w_max - w_min)*(f_max - f_i)/(f_max - f_avg);
            else
                w = w_max;
            end
        else
            w = w_max;
        end
        v(i,:) = w*v(i,:) + c1*rand(1)*(pbest(i,:) - x(i,:)) + c2*rand(1)*(gbest - x(i,:));  % 更新第i个粒子的速度
        % 如果粒子的速度超过了最大速度限制，就对其进行调整
        for j = 1: narvs
            if v(i,j) < -vmax(j)
                v(i,j) = -vmax(j);
            elseif v(i,j) > vmax(j)
                v(i,j) = vmax(j);
            end
        end
        x(i,:) = x(i,:) + v(i,:); % 更新第i个粒子的位置
        % 如果粒子的位置超出了定义域，就对其进行调整
        for j = 1: narvs
            if x(i,j) < x_lb(j)
                x(i,j) = x_lb(j);
            elseif x(i,j) > x_ub(j)
                x(i,j) = x_ub(j);
            end
        end
        fit(i) = Obj_fun1(x(i,:));  % 重新计算第i个粒子的适应度
        if fit(i) > Obj_fun1(pbest(i,:))   % 如果第i个粒子的适应度大于这个粒子迄今为止找到的最佳位置对应的适应度
            pbest(i,:) = x(i,:);   % 更新第i个粒子迄今为止找到的最佳位置
        end
        if  fit(i) > Obj_fun1(gbest)  % 如果第i个粒子的适应度大于所有的粒子迄今为止找到的最佳位置对应的适应度
            gbest = pbest(i,:);   % 更新所有粒子迄今为止找到的最佳位置
        end
    end
    fitnessbest(d) = Obj_fun1(gbest);  % 更新第d次迭代得到的最佳的适应度
    pause(0.1)  % 暂停0.1s
    h.XData = x;  % 更新散点图句柄的x轴的数据
    h.YData = fit; % 更新散点图句柄的y轴的数据
end

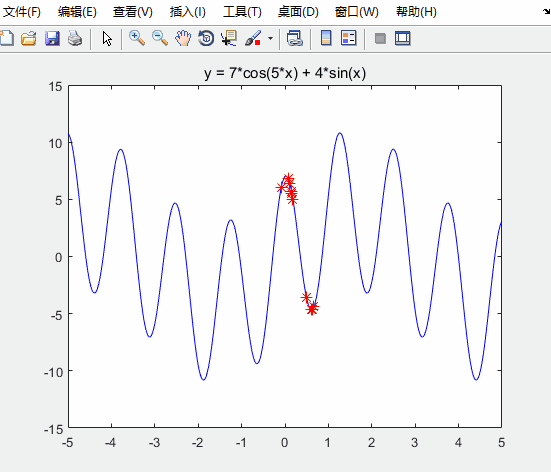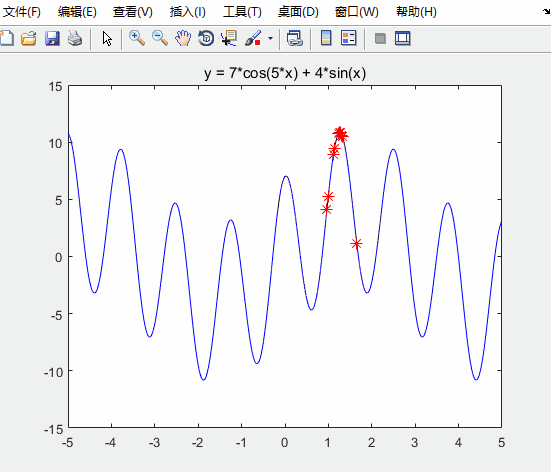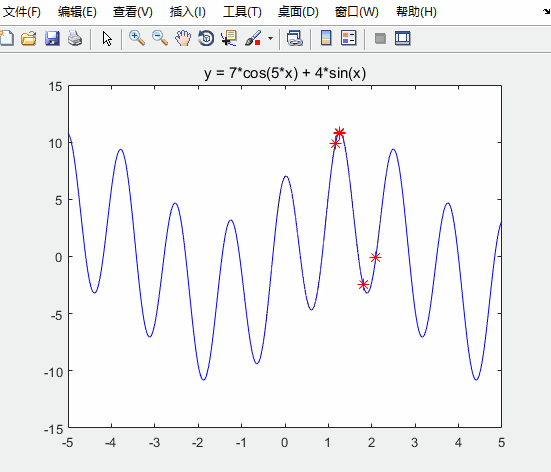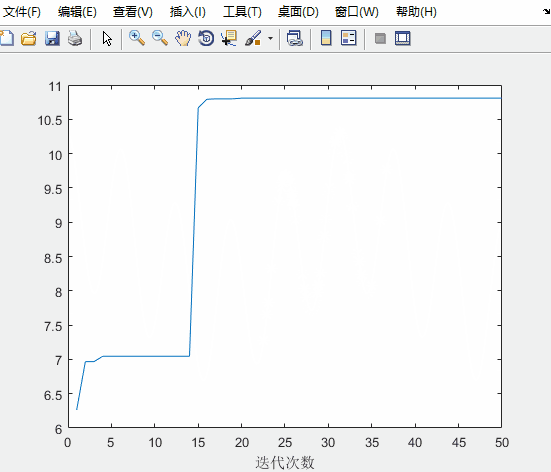
figure(2)
plot(fitnessbest)  % 绘制出每次迭代最佳适应度的变化图
xlabel('迭代次数');
disp('最佳的位置是：'); disp(gbest)
disp('此时最优值是：'); disp(Obj_fun1(gbest))

function y = Obj_fun1(x)
    y = 7*cos(5*x) + 4*sin(x);
end

运行结果如下

对比未经优化的粒子群算法
可知：求得的最优解更接近实际最优解