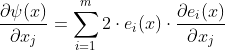【算法系列】非线性最小二乘-高斯牛顿法

  系列文章目录

·【算法系列】卡尔曼滤波算法

·【算法系列】非线性最小二乘求解-直接求解法

·【算法系列】非线性最小二乘求解-梯度下降法

·【算法系列】非线性最小二乘-高斯牛顿法

·【算法系列】非线性最小二乘-列文伯格马夸尔和狗腿算法 

文章目录

系列文章

文章目录

前言

一、牛顿法

二、高斯-牛顿法

1.由牛顿法推导

2.直接展开推导

总结

---

前言

SLAM问题常规的解决思路有两种，一种是基于滤波器的状态估计，围绕着卡尔曼滤波展开；另一种则是基于图论（因子图）的状态估计，将SLAM问题建模为最小二乘问题，而且一般是非线性最小二乘估计去求解。

非线性最小二乘有多种解法，本篇博客介绍高斯-牛顿法求解最小二乘问题。

---

非线性最小二乘的一般形式如下：

其中​​是非线性函数，​​表示协方差矩阵

为了阐述方便，进行如下表示：

​

一、牛顿法

牛顿法是采用二阶泰勒展开对函数进行近似，然后在近似局部域中找到局部最小值，并作为下一个迭代点，二阶展开是一条抛物线，该抛物线在展开点处与相切，由下图可以看到，当展开点在目标点附近时，下一步迭代点非常接近目标点。

对于一维变量，进行二阶泰勒展开，展开过程如下：

完成如上近似后，如果要求的最小值，只需要令其导数为0，求出极值点即可，并要求满足该极点处的二阶导数大于零，才能保证求出的是极小值而不是驻点或极大值。

 

解出的x值作为下一次的迭代点：

当x是一个多维变量时，展开时有所不同，其一阶导数和二阶导数都用矩阵形式表示，一阶导数叫梯度，二阶导数叫海森矩阵，展开过程如下：

同样，进行二阶泰勒展开后，对其求导，使导数等于零解出极值点，并要求满足该极点处的二阶导数大于零，才能保证求出的是极小值而不是驻点或极大值。

解出的x值作为下一次的迭代点：

整个的形式是和一维变量解出的结果相同的，一维变量是除法运算，这里变成矩阵就需要进行矩阵求逆和乘法运算。

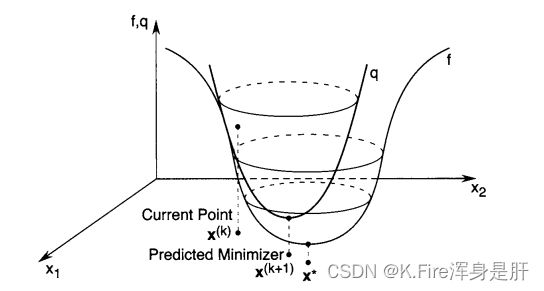
借用一下文献中的图，说明一下当变量为多维时二阶泰勒展开形成的抛物面的底部位置很接近目标点。

 牛顿法能在较少的迭代步数内使目标快速收敛，但是当变量为多维时，求海森矩阵的逆所需的计算量巨大，而且只有当展开点在目标点附近时，迭代效果才比较好，如果展开点与目标点距离较远，迭代方向可能不但不会让函数下降，反而会使结果发散。

二、高斯-牛顿法

高斯牛顿法有两个推导过程，在推导之前，需要先将代价函数做一些变形，将代价函数写成误差函数的形式，这有利于迭代过程中计算的简化，

然后分别进行介绍两种推导方法。

1.由牛顿法推导

对于误差求和，我们对其中的第i项进行研究，同样也是进行二阶泰勒展开，然后进行求导，我们先求一下它的一阶导（梯度）和二阶导（海森矩阵）

一阶导：

而就是雅克比矩阵中第j行第i列的元素，于是一阶导数又可以表示成如下形式：

二阶导：

观察二阶导的结果，前一项中的和都是雅克比矩阵中的元素，而后一项当迭代点离目标点较远时，误差和其二阶导都很小，可以忽略，所以其二阶导可以写成下式形式：

那么进行二阶展开后可以写成如下形式：

同样也是对其求导，使导数等于0得：

令则有：

对求逆很复杂，往往也会使用Cholesky分解或QR分解等数值方法求出该线性方程组的解，这样就可以得到下一次的迭代点。

2.直接展开推导

上述推导过程中，有一步我们忽略了海森矩阵包含的特别小的二阶项，其实这就等价于对误差函数进行一阶泰勒展开的线性化近似。

直接对误差函数进行一阶泰勒展开：

然后将其带入原式：

对其求导，使其导数等于0后，得到一样的结果：

MATLAB实验：

主函数：

% 目标函数为 z=f(x,y)=(x^2+y^2)/2
clear all;
clc;
%构造函数
fun = inline('(x^4+2*y^2)/2','x','y');
dfunx = inline('2*x^3','x','y');
dfuny = inline('2*y','x','y'); 
ddfunx = inline('6*x^2','x','y');
ddfuny = inline('2','x','y'); 

x0 = 2;y0 = 2;                                  %初值

[x,y,n,point] = GN(fun,dfunx,dfuny,ddfunx,ddfuny,x0,y0);    %高斯-牛顿法

figure
x = -2:0.1:4;
y = x;
[x,y] = meshgrid(x,y);
z = (x.^2+y.^2)/2;
surf(x,y,z)    %绘制三维表面图形
% hold on
% plot3(point(:,1),point(:,2),point(:,3),'linewidth',1,'color','black')
hold on
scatter3(point(:,1),point(:,2),point(:,3),'r','*');
n

GN函数：

%% 高斯牛顿法
function [x,y,n,point] = GN(fun,dfunx,dfuny,ddfunx,ddfuny,x,y)
%输入：fun:函数形式 dfunx(y):梯度（导数）ddfunx(y):海森矩阵（二阶导数） x(y):初值
%输出：x(y):计算出的自变量取值 n:迭代次数 point:迭代点集

%初始化
a = feval(fun,x,y);                                 %初值
n=1;                                                %迭代次数
point(n,:) = [x y a];   
while (1) 
  a = feval(fun,x,y);                               %当前时刻值
  x = x - (feval(dfunx,x,y))/(feval(ddfunx,x,y));   %下一时刻自变量
  y = y - (feval(dfunx,x,y))/(feval(ddfunx,x,y));   %下一时刻自变量
  b = feval(fun,x,y);                               %下一时刻值   
  a
  b
  if(b>=a)
      break;
  end
  n = n+1;
  point(n,:) = [x y b]; 
end

实验结果：

---

总结

高斯-牛顿算法在迭代点上做展开近似，当展开点附近区域线性度好，比最速下降法快很多，但当展开点附近线性度较差时，效果不佳，高斯-牛顿不一定下降，因为不一定是正定矩阵，而接下来的列文伯格-马夸尔方法和狗腿算法将解决这一问题。