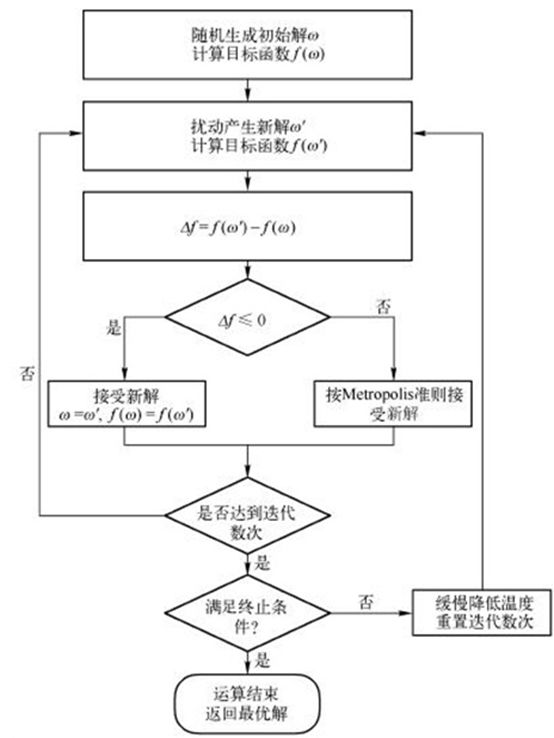
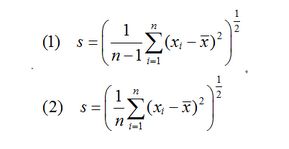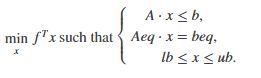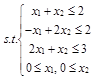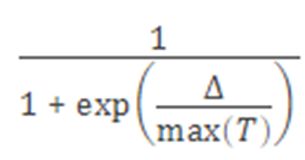MATLAB(1)
MATLAB
第一章 MATALB基础技能
第1节 MATLAB窗口
1、语言修改
中文版:预设——MATLAB——常规
英文版:Preferences——MATLAB——General
2、布局
中文版:布局
英文版:layout
3、帮助
可以搜索一些指令
第2节 命令行
1、常用指令及格式
(1)清除操作
clc 清理命令行显示
clear 清理变量
close all 关闭所有绘图窗口
clf 清除当前图像窗口
(2)快捷键
上下键:调用之前输入过的一些命令
esc:删除刚输入的一段
(3)换行操作
%命令行的换行输入
a=1 % 按Shift+Enter快捷键暂不执行此行命令,并进入下一行输入
b=2 % 按 Shift+Enter快捷键进入下一行输入,此时还可以编辑本行或上面一行命令
c=a+b % 按回车键运行全部3行命令
%当用户输入有关键词的多行循环命令时,例如for和end,并不需要使用Shift+Enter快捷键,直接按回车键即可
%进入下一行输入,直到完成了循环体之后,MATLAB才会将各行程序一起执行。
for r=1:5 % 按回车键
a=pi*r^2 % 按回车键
end % 按回车键并执行循环体内的命令
a =
3.1416
a =
12.5664
a =
28.2743
a =
50.2655
a =
78.5398
%在同一行内输入多个函数
>> x = (1:10)'; logs = [x log10(x)]
logs =
1.0000 0
2.0000 0.3010
3.0000 0.4771
4.0000 0.6021
5.0000 0.6990
6.0000 0.7782
7.0000 0.8451
8.0000 0.9031
9.0000 0.9542
10.0000 1.0000
%长命令行的分行输入
>> headers = ['Author First Name, Author Middle Initial ' ...
'Author Last Name ']
headers =
'Author First Name, Author Middle Initial Author Last Name '
>> headers = ['Author First Name, Author Middle Initial ' 'Author Last Name ']
headers =
'Author First Name, Author Middle Initial Author Last Name '
%标识符(...)如果出现在两个单引号的中间,MATLAB则会报错
%headers = ['Author Last Name, Author First Name, ...
%Author Middle Initial']
%如果一行数据太多,想分行输入,那么需要加标识符(...),不可以直接换行
>> a=[1 2 3 4 5 ...
6 7 8]
a =
1 2 3 4 5 6 7 8
% a=[1 2 3 4 5
% 6 7 8]
(4)数据显示格式
%数据显示格式
%默认显示:四舍五入,小数点后保留四位(但是后台存的是正常的数据)
>> aq=302.45
aq =
302.4500
>> a=302.00045
a =
302.0005
>> format long
>> a=302.0045
a =
3.020045000000000e+02
>> format short
>> a=302.0045
a =
302.0045
format long
format short
format compact:紧凑显示(空行少)
format loose:松散显示(空行多)
(5)科学计数法
>> a=10000000000000000000000000000000000000
a =
1.0000e+37
>> b=100e35
b =
1.0000e+37
>> c=0.0000000000021
c =
2.1000e-12
(6)随机种子设置
不同版本设置方式有所不同,根据提示来
% rand('state', 0); % 14b之后
% rng(0) % 17a之后
rng(0) %设置完之后,每次生成的随机数都一样的,方便验证数据
>> rng(0)
>> randperm(7) % 创建由1∶7构成的随机数列(每次输入完rng(0),生成的随机序列便如下)
ans =
6 3 7 5 1 2 4
2、变量赋值
>> a=1
a =
1
3、矩阵操作
(1)矩阵输入
% 换行分号,行末分号
>> A = [1 2 3; 4 5 6; 7 8 10]
A =
1 2 3
4 5 6
7 8 10
%行末加分号则不在命令行窗口显示结果,但是会存入内存空间
>> A = [1 2 3; 4 5 6; 7 8 10];
>>
(2)矩阵合并
>> A = ones(2, 5) * 6 % 元素全部为6的2´5矩阵
A =
6 6 6 6 6
6 6 6 6 6
>> B= rand(3, 5) % 3´5 的随机数矩阵
B =
0.8147 0.9134 0.2785 0.9649 0.9572
0.9058 0.6324 0.5469 0.1576 0.4854
0.1270 0.0975 0.9575 0.9706 0.8003
>> C = [A; B] %换行,上下合并
C =
6.0000 6.0000 6.0000 6.0000 6.0000
6.0000 6.0000 6.0000 6.0000 6.0000
0.8147 0.9134 0.2785 0.9649 0.9572
0.9058 0.6324 0.5469 0.1576 0.4854
0.1270 0.0975 0.9575 0.9706 0.8003
>> A = ones(3, 5) * 6
A =
6 6 6 6 6
6 6 6 6 6
6 6 6 6 6
>> C = [A B] %在维度一致的情况下,左右合并
C =
1 至 7 列
6.0000 6.0000 6.0000 6.0000 6.0000 0.8147 0.9134
6.0000 6.0000 6.0000 6.0000 6.0000 0.9058 0.6324
6.0000 6.0000 6.0000 6.0000 6.0000 0.1270 0.0975
8 至 10 列
0.2785 0.9649 0.9572
0.5469 0.1576 0.4854
0.9575 0.9706 0.8003
(3)矩阵的赋值
>> a=magic(4)
a =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> a(3,4)=0 % 对单个元素进行赋值
a =
16 2 3 13
5 11 10 8
9 7 6 0
4 14 15 1
>> a(:,1)=1 % 对第一列进行赋值
a =
1 2 3 13
1 11 10 8
1 7 6 0
1 14 15 1
>> a(14)=16 % 采用全下标对第14个元素进行赋值
a =
1 2 3 13
1 11 10 16
1 7 6 0
1 14 15 1
>> ones(4) % 创建所有元素为1的矩阵
ans =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
>> rand(2,3) % 创建2*3的均匀分布随机数矩阵,赋值范围为0-1
ans =
0.1419 0.9157 0.9595
0.4218 0.7922 0.6557
>> randperm(7) % 创建由1∶7构成的随机数列
ans =
1 7 4 6 5 2 3
(4)数组运算与矩阵运算
>> a=[1 2 4 9;16 25 36 49]
a =
1 2 4 9
16 25 36 49
>> b=sqrt(a) % 应用函数对矩阵中的每一个元素分别开方
b =
1.0000 1.4142 2.0000 3.0000
4.0000 5.0000 6.0000 7.0000
>> A=[1 2;3 4] % 测试矩阵A
A =
1 2
3 4
>> B=[4 3;2 1] % 测试矩阵B
B =
4 3
2 1
>> r1=100+A % 矩阵A加上一个常数
r1 =
101 102
103 104
>> r2_1=A*B % 两个矩阵相乘,矩阵乘法
r2_1 =
8 5
20 13
>> r2_2=A.*B % 两个矩阵相乘,数组乘法
r2_2 =
4 6
6 4
>> r3_1=A\B % 矩阵左除
r3_1 =
-6.0000 -5.0000
5.0000 4.0000
>> r3_2=A.\B % 数组除法
r3_2 =
4.0000 1.5000
0.6667 0.2500
>> r4_1=B/A % 矩阵右除
r4_1 =
-3.5000 2.5000
-2.5000 1.5000
>> r4_2=B./A % 数组除法
r4_2 =
4.0000 1.5000
0.6667 0.2500
>> r5_2=A^2 % 矩阵幂
r5_2 =
7 10
15 22
>> r5_1=A.^2 % 数组幂
r5_1 =
1 4
9 16
>> r6_1=2.^A % 数组幂
r6_1 =
2 4
8 16
(5)矩阵元素的扩展与删除
>> A=magic(4)
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> A(6,7)=17
A =
16 2 3 13 0 0 0
5 11 10 8 0 0 0
9 7 6 12 0 0 0
4 14 15 1 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 17
>> A(:,8)=ones(6,1)
A =
16 2 3 13 0 0 0 1
5 11 10 8 0 0 0 1
9 7 6 12 0 0 0 1
4 14 15 1 0 0 0 1
0 0 0 0 0 0 0 1
0 0 0 0 0 0 17 1
>> A(:,1)=[] % 删除矩阵A的第1列
A =
2 3 13 0 0 0 1
11 10 8 0 0 0 1
7 6 12 0 0 0 1
14 15 1 0 0 0 1
0 0 0 0 0 0 1
0 0 0 0 0 17 1
>> A(2,:)=[] % 删除矩阵A的第2行
A =
2 3 13 0 0 0 1
7 6 12 0 0 0 1
14 15 1 0 0 0 1
0 0 0 0 0 0 1
0 0 0 0 0 17 1
(6)矩阵的重构
>> a=reshape(1:9,3,3) % 创建测试矩阵
a =
1 4 7
2 5 8
3 6 9
>> a= [1,7;2,8;3,9;4,10;5,11;6,12] % 创建测试矩阵
a =
1 7
2 8
3 9
4 10
5 11
6 12
>> a = reshape(a,4,3) % 使用reshape改变a的形状,注意前后两个a每一个单下标对应的元素是一致的
a =
1 5 9
2 6 10
3 7 11
4 8 12
>> b=rot90(a,3) % 将矩阵a逆时针旋转3×90°
b =
4 3 2 1
8 7 6 5
12 11 10 9
>> c=fliplr(a) % 将矩阵a左右翻转
c =
9 5 1
10 6 2
11 7 3
12 8 4
>> d=flipud(a) % 将矩阵a上下翻转
d =
4 8 12
3 7 11
2 6 10
1 5 9
(7)矩阵的形状信息
>> A = rand(5,3) * 10 % 生成5*3的随机矩阵
A =
2.7603 4.9836 7.5127
6.7970 9.5974 2.5510
6.5510 3.4039 5.0596
1.6261 5.8527 6.9908
1.1900 2.2381 8.9090
>> size(A)
ans =
5 3
>> a=length(A) %最长的那个方向的长度
a =
5
>> A = A' %转置
A =
2.7603 6.7970 6.5510 1.6261 1.1900
4.9836 9.5974 3.4039 5.8527 2.2381
7.5127 2.5510 5.0596 6.9908 8.9090
>> a=length(A)
a =
5
>> b=sum(A(:))/numel(A) % 使用Sum和numel函数计算矩阵A的平均值
b =
5.0682
>> numel(A)
ans =
15
>> mean(A) %求每一列的平均数
ans =
5.0855 6.3151 5.0048 4.8232 4.1124
>> mean(A,2) %求每一行平均数
ans =
3.7849
5.2151
6.2046
>> mean(A(:)) %求所有元素的平均数
ans =
5.0682
>> mean(mean(A)) %先对所有列求平均数,求完平均再求平均
ans =
5.0682
4、数据计算
>> b=29*(2+23/3)-5^2
b =
255.3333
5、函数的调用
语法格式:返回值=函数名(参数1,参数2,……)
注意:Tab键补全功能,语法提示,错误纠正
plot函数:输入”plot(“,等一会儿,会自动显示
magic(3:直接输入enter,会报错,可以根据箭头指向位置以及错误提示修改
Sin(pi):直接输入enter,会报错,可以根据错误提示修改,sin是区分大小写的
mean(c,'o:按下Tab,会出现自动补全
%生成3*3的幻方,行,列,对角线和都相等
>> d=magic(3)
d =
8 1 6
3 5 7
4 9 2
% mean(a,'omitnan'),忽略NAN值求平均数
>> c=1:10
c =
1 2 3 4 5 6 7 8 9 10
>> mean(c,'omitnan')
ans =
5.5000
>> c(4)=NaN
c =
1 2 3 NaN 5 6 7 8 9 10
>> mean(c,'omitnan')
ans =
5.6667
>> mean(c)
ans =
NaN
6、常用变量名
% ans:默认赋值结果变量名,但是会被不断覆盖
>> 2+3
ans =
5
% NAN:not a number
>> 0/0
ans =
NaN
% Inf:无穷大
>> 2/0
ans =
Inf
% i或j:虚数单位
>> i
ans =
0.0000 + 1.0000i
>> j
ans =
0.0000 + 1.0000i
>> 2+3i
ans =
2.0000 + 3.0000i
% pi:圆周率
>> pi
ans =
3.1416
% eps:相对精度,两个量最小可以差这么多(并不是MATLAB软件造成的,是计算机二进制系统造成的)
>> eps
ans =
2.2204e-16
>> a=10000000000000000
b=10000000000000001
a =
1.0000e+16
b =
1.0000e+16
>> c=a-b
c =
0
>> c==0
ans =
logical
1
>> a1=1000000000000000
b1=1000000000000001
a1 =
1.0000e+15
b1 =
1.0000e+15
>> c1=a1-b1
c1 =
-1
>> c1==0
ans =
logical
0
7、复数相关函数
>> sd=5+6i
sd =
5.0000 + 6.0000i
>> r=real(sd) % 给出复数sd的实部
r =
5
>> im=imag(sd) % 给出复数sd的虚部
im =
6
%复数 z=a+bi(a,b∈R)
%则模为√(a²+b²)
%相位角设为W,arctanW=b/a
>> a=abs(sd) % 给出复数sd的模/绝对值
a =
7.8102
>> an=angle(sd) % 以弧度为单位给出复数sd的相位角,angle 函数可以写为 atan2( imag (h), real (h) )
an =
0.8761
>> A=[2,4;1,6]-[3,7;3,9]*i
A =
2.0000 - 3.0000i 4.0000 - 7.0000i
1.0000 - 3.0000i 6.0000 - 9.0000i
>> B=[2+5i,3+2i;6-9i,3-5i]
B =
2.0000 + 5.0000i 3.0000 + 2.0000i
6.0000 - 9.0000i 3.0000 - 5.0000i
>> C=B-A
C =
0.0000 + 8.0000i -1.0000 + 9.0000i
5.0000 - 6.0000i -3.0000 + 4.0000i
8、开立方根
>> a=-8
a =
-8
>> r=a^(1/3)
r =
1.0000 + 1.7321i
% 结果不为-2,因为在数学中开立方有三个解,有两个解是复数解,-2是实数解
>> R=abs(a)^(1/3) % 模的开3次方
R =
2
>> m=[0,1,2]; % 为3个方根而设
>> theta=(angle(a)+2*pi*m)/3 % -pi> r=R*exp(i*theta) % 将得到的结果赋给r
r =
1.0000 + 1.7321i -2.0000 + 0.0000i 1.0000 - 1.7321i
角度和弧度:1°=π/180°,1rad=180°/π
角度转弧度 π/180×角度;弧度变角度 180/π×弧度。
复数的立方根求法:
把复数变成幅度和相角的形式
例如a+bi:
幅度为:√(a^2 + b^2)
相角为:arctan(b/a)
开立方根:幅度开立方根,相角变成原来的1/3
得到3个复数,幅度相同,相角不同,它们都是原来那个数的立方根。
比如:求1的立方根:
先把1化成幅度和相角的形式:
幅度为1,相角为360k°(k=0,1,2,…)
开立方根:幅度开立方根,1开立方根还是1
相角变成原来的1/3:360k°/3=120k°(k=0,1,2,…)
所以相角有3种:0°,120°,240°。
得到3个立方根:
幅度1,相角0°;幅度1,相角120°;幅度1,相角240°
再化为a+bi的形式就是:
1 ; -1/2+(√3)i/2 ; -1/2-(√3)i/2
9、空格、冒号
(1)空格的作用
>> a1=7 -2 +5
a2=7 - 2 +5
a3=[7 - 2 + 5]
a4=[7 -2 +5]
a1 =
10
a2 =
10
a3 =
10
a4 =
7 -2 5
(2)冒号的作用
>> a=2:2:20
a =
2 4 6 8 10 12 14 16 18 20
>> b=10:-1:2
b =
10 9 8 7 6 5 4 3 2
>> b=10:1:2
b =
空的 1×0 double 行向量
>> a=1:5
a =
1 2 3 4 5
>> a=[1 2 3; 4 5 6] % 创建测试矩阵
a =
1 2 3
4 5 6
>> d=a(1,:) % 通过使用冒号可以寻访全行元素
d =
1 2 3
>> e=a(:,2) % 通过使用冒号可以寻访全列元素
e =
2
5
>> f=a(:) % 单下标寻访
f =
1
4
2
5
3
6
>> g=a(:,[1 3]) % 寻访地址可以是向量,以同时寻访多个元素
g =
1 3
4 6
10、下标
>> a=[1 2 3; 4 5 6] % 创建测试矩阵
a =
1 2 3
4 5 6
>> A=a(2,2) % 全下标寻访,第2行第2列
A =
5
>> b=a(4) % 单下标寻访 (访问顺序:按列,1,4,2,5)
b =
5
% 逻辑1标识
>> B=a>5 % 返回逻辑下标
B =
2×3 logical 数组
0 0 0
0 0 1
>> c=a(B) % 逻辑下标寻访
c =
6
>> C=a(a>5)
C =
6
11、多维数组:
创建多维数组最常用的方法有以下4种:
(1)直接通过“全下标”元素赋值的方式创建多维数组。
(2)由若干同样尺寸的二维数组组合成多维数组。
(3)由函数ones、zeros、rand、randn等直接创建特殊多维数组。
(4)借助cat、repmat、reshape等函数构建多维数组。
%三维数组:几行几列几页
>> A(3,3,3)=1 % 创建3*3*3数组,未赋值元素默认设置为0
A(:,:,1) =
0 0 0
0 0 0
0 0 0
A(:,:,2) =
0 0 0
0 0 0
0 0 0
A(:,:,3) =
0 0 0
0 0 0
0 0 1
>> B(3,4,:)=1:4 % 创建3*4*4数组
B(:,:,1) =
0 0 0 0
0 0 0 0
0 0 0 1
B(:,:,2) =
0 0 0 0
0 0 0 0
0 0 0 2
B(:,:,3) =
0 0 0 0
0 0 0 0
0 0 0 3
B(:,:,4) =
0 0 0 0
0 0 0 0
0 0 0 4
>> C(:,:,1)=magic(4); % 创建数组A第1页的数据
C(:,:,2)=ones(4); % 创建数组A第2页的数据
C(:,:,3)=zeros(4) % 创建数组A第3页的数据
C(:,:,1) =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
C(:,:,2) =
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
C(:,:,3) =
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
>> D=rand(3,4,3) % 由函数rand直接创建特殊多维数组
D(:,:,1) =
0.8003 0.9157 0.6557 0.9340
0.1419 0.7922 0.0357 0.6787
0.4218 0.9595 0.8491 0.7577
D(:,:,2) =
0.7431 0.1712 0.2769 0.8235
0.3922 0.7060 0.0462 0.6948
0.6555 0.0318 0.0971 0.3171
D(:,:,3) =
0.9502 0.3816 0.1869 0.6463
0.0344 0.7655 0.4898 0.7094
0.4387 0.7952 0.4456 0.7547
% cat()函数,后面那个数字,表示在第几维度上拼
>> E3=cat(3,ones(2,3),ones(2,3)*2,ones(2,3)*3) %借助cat函数构建多维数组
E3(:,:,1) =
1 1 1
1 1 1
E3(:,:,2) =
2 2 2
2 2 2
E3(:,:,3) =
3 3 3
3 3 3
>> E2=cat(2,ones(2,3),ones(2,3)*2,ones(2,3)*3) %借助cat函数构建多维数组
E2 =
1 1 1 2 2 2 3 3 3
1 1 1 2 2 2 3 3 3
>> E1=cat(1,ones(2,3),ones(2,3)*2,ones(2,3)*3) %借助cat函数构建多维数组
E1 =
1 1 1
1 1 1
2 2 2
2 2 2
3 3 3
3 3 3
>> e=[1,2;3,4;5,6]
e =
1 2
3 4
5 6
>> F=repmat(e,[1,2,3]) %行这一维重复一遍,列这一维度重复两遍,页这一维度重复三遍
F(:,:,1) =
1 2 1 2
3 4 3 4
5 6 5 6
F(:,:,2) =
1 2 1 2
3 4 3 4
5 6 5 6
F(:,:,3) =
1 2 1 2
3 4 3 4
5 6 5 6
>> G=reshape(1:60,5,4,3)
G(:,:,1) =
1 6 11 16
2 7 12 17
3 8 13 18
4 9 14 19
5 10 15 20
G(:,:,2) =
21 26 31 36
22 27 32 37
23 28 33 38
24 29 34 39
25 30 35 40
G(:,:,3) =
41 46 51 56
42 47 52 57
43 48 53 58
44 49 54 59
45 50 55 60
>> H=reshape(G,4,5,3)
H(:,:,1) =
1 5 9 13 17
2 6 10 14 18
3 7 11 15 19
4 8 12 16 20
H(:,:,2) =
21 25 29 33 37
22 26 30 34 38
23 27 31 35 39
24 28 32 36 40
H(:,:,3) =
41 45 49 53 57
42 46 50 54 58
43 47 51 55 59
44 48 52 56 60
>> I=flip(H,1) %数组翻转(第一维度上下翻转)
I(:,:,1) =
4 8 12 16 20
3 7 11 15 19
2 6 10 14 18
1 5 9 13 17
I(:,:,2) =
24 28 32 36 40
23 27 31 35 39
22 26 30 34 38
21 25 29 33 37
I(:,:,3) =
44 48 52 56 60
43 47 51 55 59
42 46 50 54 58
41 45 49 53 57
>> J=shiftdim(H,1) % 将各维向左移动1位,使2*3*3数组变成3*3*2数组
J(:,:,1) =
1 21 41
5 25 45
9 29 49
13 33 53
17 37 57
J(:,:,2) =
2 22 42
6 26 46
10 30 50
14 34 54
18 38 58
J(:,:,3) =
3 23 43
7 27 47
11 31 51
15 35 55
19 39 59
J(:,:,4) =
4 24 44
8 28 48
12 32 52
16 36 56
20 40 60
>> K=shiftdim(H,2) % 将各维向左移动2位,使2*3*3数组变成3*2*3数组
K(:,:,1) =
1 2 3 4
21 22 23 24
41 42 43 44
K(:,:,2) =
5 6 7 8
25 26 27 28
45 46 47 48
K(:,:,3) =
9 10 11 12
29 30 31 32
49 50 51 52
K(:,:,4) =
13 14 15 16
33 34 35 36
53 54 55 56
K(:,:,5) =
17 18 19 20
37 38 39 40
57 58 59 60
%运算D=shiftdim(A,1)实现以下操作:D(j,k,i)=A(i,j,k),i, j, k分别是指各维的下标。对于三维数组,%D=shiftdim(A,3)的操作就等同于简单的D=A。
第3节 数据类型
1、逻辑型
运算优先级
>> a=[1 2 3; 4 5 6] % 创建测试矩阵
a =
1 2 3
4 5 6
>> B=a>5 % 返回逻辑下标
B =
2×3 logical 数组
0 0 0
0 0 1
>> aa = true
aa =
logical
1
>> bb = false
bb =
logical
0
>> c=true(size(a))
c =
2×3 logical 数组
1 1 1
1 1 1
>> false([size(a),2])
2×3×2 logical 数组
ans(:,:,1) =
0 0 0
0 0 0
ans(:,:,2) =
0 0 0
0 0 0
>> a=[1 2 3;4 5 6]
a =
1 2 3
4 5 6
>> b=[1 0 0;0 -2 1]
b =
1 0 0
0 -2 1
>> A=a&b % 逻辑“与”
A =
2×3 logical 数组
1 0 0
0 1 1
>> B=a|b % 逻辑“或”
B =
2×3 logical 数组
1 1 1
1 1 1
>> C=~b % 逻辑“非”
C =
2×3 logical 数组
0 1 1
1 0 0
>> a=[1 1 0; 1 0 0;1 0 1]
a =
1 1 0
1 0 0
1 0 1
>> A=all(a) % 每列元素均为非零时返回真
A =
1×3 logical 数组
1 0 0
>> D=all(a,2) % 每行元素均为非零时返回真
D =
3×1 logical 数组
0
0
0
>> B=any(a) % 每列元素存在非零时返回真
B =
1×3 logical 数组
1 1 1
>> C=any(a,2) % 每行元素存在非零时返回真
C =
3×1 logical 数组
1
1
1
>> a=[0 -1 2]
a =
0 -1 2
>> b=[-3 1 2]
b =
-3 1 2
>> a> a>b % 对应元素比较大小
ans =
1×3 logical 数组
1 0 0
>> a<=b % 对应元素比较大小
ans =
1×3 logical 数组
0 1 1
>> a>=b % 对应元素比较大小
ans =
1×3 logical 数组
1 0 1
>> a==b % 对应元素比较相等
ans =
1×3 logical 数组
0 0 1
>> a~=b % 对应元素比较不相等
ans =
1×3 logical 数组
1 1 0
2、字符串
>> a='matlab'
a =
'matlab'
>> size(a)
ans =
1 6
>> A='中文字符串输入演示'
A =
'中文字符串输入演示'
>> A(3:5)
ans =
'字符串'
>> S=['This string array '
'has multiple rows.']
S =
2×18 char 数组
'This string array '
'has multiple rows.'
>> a=char('这','字符','串数组','','由5 行组成')
% 以字符最多的一行为准,而将其他行中的字符以空格补齐
a =
5×6 char 数组
'这 '
'字符 '
'串数组 '
' '
'由5 行组成'
>> size(a)
ans =
5 6
>> str1 = 'hello';
str2 = 'help';
>> C = strcmp(str1,str2)
C =
logical
0
>> C = strncmp(str1, str2, 2) % 比较前两个字符
C =
logical
1
>> str3 = 'Hello';
>> D = strncmp(str1, str3,2) % 对大小写敏感
D =
logical
0
>> F = strncmpi(str1, str3,2) % 对大小写不敏感
F =
logical
1
>> A = 'fate';
B = 'cake';
A == B %使用(==)运算符来判断两个字符串中有哪些字符相等
ans =
1×4 logical 数组
0 1 0 1
>> a=1
a =
1
>> b=num2str(a)
b =
'1'
>> c=str2num(b)
c =
1
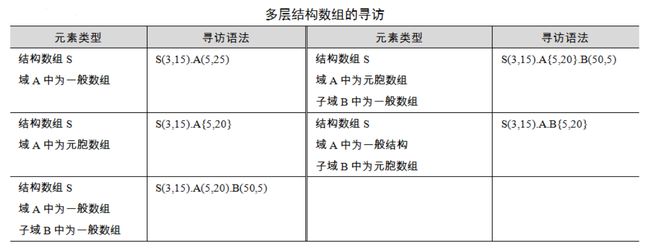
3、结构数组
>> employee.name='henry';
employee.sex='male';
employee.age=25;
employee.number=12345;
employee
employee =
包含以下字段的 struct:
name: 'henry'
sex: 'male'
age: 25
number: 12345
>> employee(2).name='lee';
employee(2).sex='female';
employee(2).age=23;
employee(2).number=98765;
employee(2)
ans =
包含以下字段的 struct:
name: 'lee'
sex: 'female'
age: 23
number: 98765
>> employee % 查看employee结构数组
employee =
包含以下字段的 1×2 struct 数组:
name
sex
age
number
子域
>> green_house.name='一号房';
green_house.volume='2000 立方米';
green_house.parameter.temperature=...
[31.2 30.4 31.6 28.7;29.7 31.1 30.9 29.6]; %子域温度
green_house.parameter.humidity=...
[62.1 59.5 57.7 61.5;62.0 61.9 59.2 57.5]; %子域湿度
>> green_house.parameter % 显示域的内容
ans =
包含以下字段的 struct:
temperature: [2×4 double]
humidity: [2×4 double]
>> green_house.parameter.temperature % 显示子域中的内容
ans =
31.2000 30.4000 31.6000 28.7000
29.7000 31.1000 30.9000 29.6000
>> USPres.name = 'Franklin D. Roosevelt';
USPres.vp(1) = {'John Garner'};
USPres.vp(2) = {'Henry Wallace'};
USPres.vp(3) = {'Harry S Truman'};
USPres.term = [1933, 1945];
USPres.party = 'Democratic'; % 创建包括4个域名的结构数组
presFields = fieldnames(USPres) % 使用fieldnames函数获取现有域名
presFields =
4×1 cell 数组
{'name' }
{'vp' }
{'term' }
{'party'}
>> orderfields(USPres) % 使用orderfields函数对域名按照字母顺序进行排序
ans =
包含以下字段的 struct:
name: 'Franklin D. Roosevelt'
party: 'Democratic'
term: [1933 1945]
vp: {'John Garner' 'Henry Wallace' 'Harry S Truman'}
>> mystr1 = getfield(USPres, 'name') % 获取结构的域内容
mystr1 =
'Franklin D. Roosevelt'
>> mystr2= setfield(USPres, 'name', 'ted') % 设置结构的域内容
mystr2 =
包含以下字段的 struct:
name: 'ted'
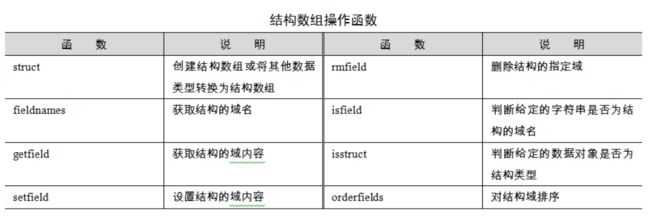
vp: {'John Garner' 'Henry Wallace' 'Harry S Truman'}
term: [1933 1945]
party: 'Democratic'
>> USPres.name = 'Franklin D. Roosevelt';
USPres.vp(1) = {'John Garner'};
USPres.vp(2) = {'Henry Wallace'};
USPres.vp(3) = {'Harry S Truman'};
USPres.term = [1933, 1945];
USPres.party = 'Democratic'; % 创建包括4个域名的结构数组
>> USPres(3,2).name='Richard P. Jackson' % 结构数组的扩展
USPres =
包含以下字段的 3×2 struct 数组:
name
vp
term
party
>> USPres(2,:)=[] % 通过对结构数组赋值为空矩阵来实现删除
USPres =
包含以下字段的 2×2 struct 数组:
name
vp
term
party
% emmm,具体点开那个变量就懂了
4、元胞数组
元胞数组有下标,做循环更方便
结构数组有域名,编程更为方便
(1)创建元胞数组
使用{}
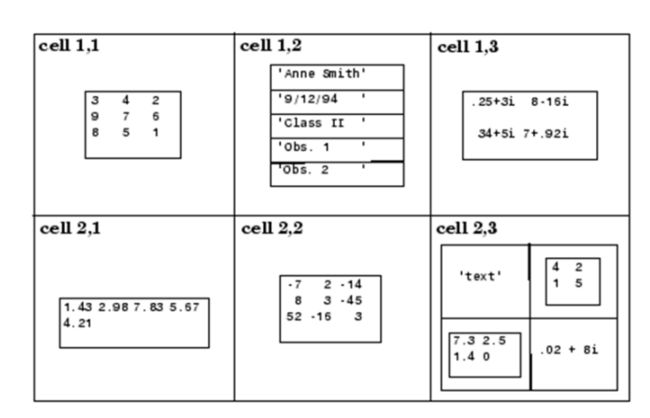
>> A = {[1 4 3; 0 5 8; 7 2 9], 'Anne Smith'; 3+7i, -pi:pi/4:pi}
A =
2×2 cell 数组
{3×3 double } {'Anne Smith'}
{[3.0000 + 7.0000i]} {1×9 double }
>> header = {'Name', 'Age', 'Pulse/Temp/BP'} % 元胞数组的创建
header =
1×3 cell 数组
{'Name'} {'Age'} {'Pulse/Temp/BP'}
>> records(1,:) = {'Kelly', 49, {58, 98.3, [103, 72]}} % 嵌套元胞数组的创建
records =
1×3 cell 数组
{'Kelly'} {[49]} {1×3 cell}
(2)依次创建元胞数组
A(1,1) = {[1 4 3; 0 5 8; 7 2 9]};
A(1,2) = {'Anne Smith'};
A(2,1) = {3+7i};
A(2,2) = {-pi:pi/4:pi};
A(3,3) = {5}
A =
3×3 cell 数组
{3×3 double } {'Anne Smith'} {0×0 double}
{[3.0000 + 7.0000i]} {1×9 double } {0×0 double}
{0×0 double } {0×0 double } {[ 5]}
>> str=A{1,2} % 返回字符型数组str,a{1,2}表示对应元胞的内容
str =
'Anne Smith'
>> class(str) % 查看变量str的数据类型,结果确为字符型
ans =
'char'
>> str2=A(1,2) % a(1,2)表示元胞数组中的一个元胞
str2 =
1×1 cell 数组
{'Anne Smith'}
>> class(str2) % 查看变量str2的数据类型,结果为元胞数组
ans =
'cell'
>> [nrows, ncols] = cellfun(@size, A) % 将size函数应用于每一个元胞元素
nrows =
3 1 0
1 1 0
0 0 1
ncols =
3 10 0
1 9 0
0 0 1
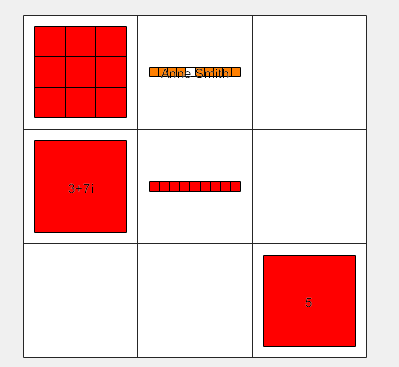
>> cellplot(A) % 以图片表示元胞数组的基本结构
5、日期时间
>> t = datetime(2017,8,28,6:7,0,0)
t =
1×2 datetime 数组
2017-08-28 06:00:00 2017-08-28 07:00:00
>> t.Day
ans =
28 28
>> t.Day = 27:28
t =
1×2 datetime 数组
2017-08-27 06:00:00 2017-08-28 07:00:00
>> t.Format
ans =
'uuuu-MM-dd HH:mm:ss'
>> t.Format = 'MMMdd日, yyyy年'
t =
1×2 datetime 数组
8月27日, 2017年 8月28日, 2017年
>> t2 = datetime(2017,7,29,6,30,45)
t2 =
datetime
2017-07-29 06:30:45
>> d = t - t2
d =
1×2 duration 数组
695:29:15 720:29:15 % 时分秒
>> d.Format = 'h'
d =
1×2 duration 数组
695.49小时 720.49小时
>> d.Format = 'd'
d =
1×2 duration 数组
28.979天 30.02天
6、表格数组
>> T = readtable('patients.dat') % 读取表格数据,matlab自带的一个数据文件
>> T(1:5,1:5)
ans =
5×5 table
LastName Gender Age Location Height
__________ ________ ___ ___________________________ ______
'Smith' 'Male' 38 'County General Hospital' 71
'Johnson' 'Male' 43 'VA Hospital' 69
'Williams' 'Female' 38 'St. Mary's Medical Center' 64
'Jones' 'Female' 40 'VA Hospital' 67
'Brown' 'Female' 49 'County General Hospital' 64
>> T.Age
创建表格数组
>> LastName = {'Smith';'Johnson';'Williams';'Jones';'Brown'};
%这里如果创建结构数组,就会报错:要串联的数组的维度不一致。
Age = [38;43;38;40;49];
Height = [71;69;64;67;64];
Weight = [176;163;131;133;119];
BloodPressure = [124 93; 109 77; 125 83; 117 75; 122 80];
T = table(LastName,Age,Height,Weight,BloodPressure)
T =
5×5 table
LastName Age Height Weight BloodPressure
__________ ___ ______ ______ _____________
'Smith' 38 71 176 124 93
'Johnson' 43 69 163 109 77
'Williams' 38 64 131 125 83
'Jones' 40 67 133 117 75
'Brown' 49 64 119 122 80
>> T.Properties.VariableNames
ans =
1×5 cell 数组
{'LastName'} {'Age'} {'Height'} {'Weight'} {'BloodPressure'}
% properties 类属性名称
% VariableNames 列名称
% RowNames 行名称
表可以像普通数值矩阵那样通过小括号加下标来进行寻访。
除了数值和逻辑型下标之外,用户还可以使用变量名和行名来作为下标。例如本例中可以使用LastName作为行名,然后将这一列数据删除。
>> T.LastName
ans =
5×1 cell 数组
{'Smith' }
{'Johnson' }
{'Williams'}
{'Jones' }
{'Brown' }
>> T.LastName = [];
>> size(T) % 查看当前表T的尺寸
ans =
5 4
>> T(1:5,3:4)
ans =
5×2 table
Weight BloodPressure
______ _____________
176 124 93
163 109 77
131 125 83
133 117 75
119 122 80
基于已有变量(身高和体重)用户可以创建新的变量BMI,也就是体重指数。然后还可以添加变量的单位和描述等属性
>> T.BMI = (T.Weight*0.453592)./(T.Height*0.0254).^2;
>> T
T =
5×5 table
Age Height Weight BloodPressure BMI
___ ______ ______ _____________ ______
38 71 176 124 93 24.547
43 69 163 109 77 24.071
38 64 131 125 83 22.486
40 67 133 117 75 20.831
49 64 119 122 80 20.426
%通过修改表属性 VariableUnits 来为表中的每个变量指定单位
>> T.Properties.VariableUnits{'BMI'} = 'kg/m^2';
%创建索引
T.Properties.VariableDescriptions{'BMI'} = 'Body Mass Index';
%对数据做了备注,但是是不显示的
>> T
T =
5×5 table
Age Height Weight BloodPressure BMI
___ ______ ______ _____________ ______
38 71 176 124 93 24.547
43 69 163 109 77 24.071
38 64 131 125 83 22.486
40 67 133 117 75 20.831
49 64 119 122 80 20.426
>> size(T) % 查看当前表的尺寸
ans =
5 5
第二章 MATALB数据可视化及图像句柄
第1节 基础绘图
1、概述
(1)绘图类型
Help ——> Types of MATLAB Plots /MATLAB绘图类型
(2)绘图步骤
(3)一般调用格式
Handle=FuntionName(data,’name’,’value’)
比如:h =plot(X,Y,name,value)
(4)图形初步了解
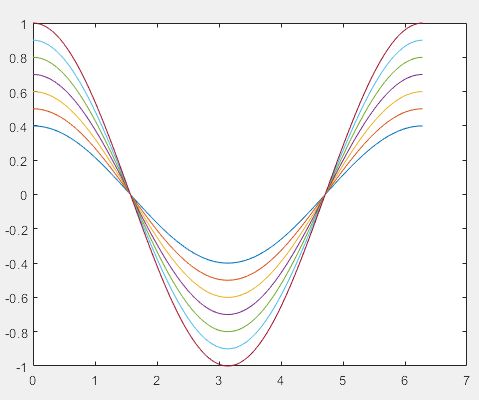
1)二维曲线图
>> t=(0:pi/50:2*pi)';
k=0.4:0.1:1;
Y=cos(t)*k;
plot(t,Y) % 绘制二维曲线图
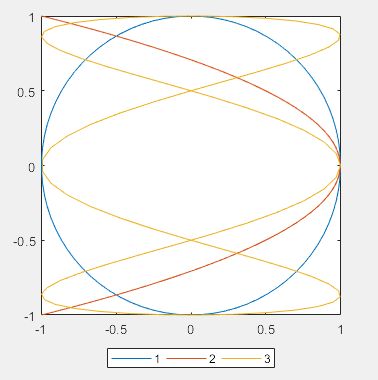
2)李萨如图形
>> t=linspace(0,2*pi,80)'; % 在[0,2pi]之间产生80个等距的采样点
X=[cos(t),cos(2*t),cos(3*t)]+1i*sin(t)*[1, 1, 1]; %(80×3)的复数矩阵
plot(X)
![]()
>> axis square % 使坐标轴长度相同
>> h1=legend('1','2','3') % 图例
h1 =
Legend (1, 2, 3) - 属性:
String: {'1' '2' '3'}
Location: 'northeast'
Orientation: 'vertical'
FontSize: 9
Position: [0.7015 0.7746 0.1036 0.1262]
Units: 'normalized'
显示 所有属性
>> h1.Location='southoutside' %将图例位置移到下面外面
h1 =
Legend (1, 2, 3) - 属性:
String: {'1' '2' '3'}
Location: 'southoutside'
Orientation: 'vertical'
FontSize: 9
Position: [0.4661 0.0881 0.1036 0.1262]
Units: 'normalized'
显示 所有属性
>> h1.Orientation='horizontal' %三个图例显示为水平方向的
h1 =
Legend (1, 2, 3) - 属性:
String: {'1' '2' '3'}
Location: 'southoutside'
Orientation: 'horizontal'
FontSize: 9
Position: [0.3679 0.0952 0.3000 0.0476]
Units: 'normalized'
显示 所有属性
% legend函数还有如下用法,其他用法请查阅帮助文档
% legend('Location','southwest')
% legend('boxoff')
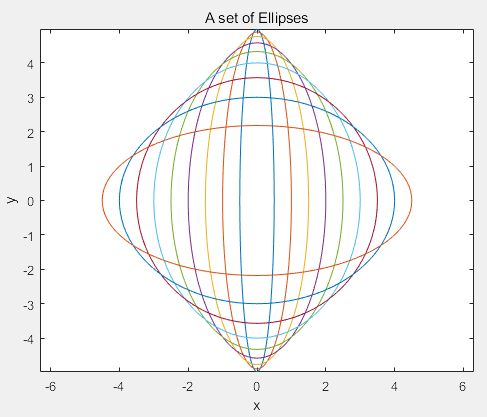
3)绘制椭圆
>> clear
>> th = [0:pi/50:2*pi]';
a = [0.5:.5:4.5];
X = cos(th)*a;
Y = sin(th)*sqrt(25-a.^2);
plot(X,Y),axis('equal'),xlabel('x'), ylabel('y')
>> title('A set of Ellipses')
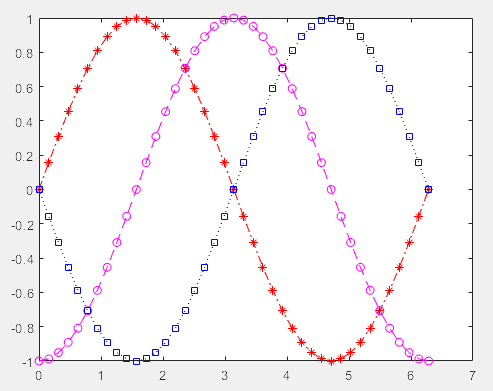
2、点型线型
>> clear
t = 0:pi/20:2*pi;
>> plot(t,sin(t),'-.r*')
>> hold on %将几条曲线绘制到同一个图上,否则会覆盖之前的曲线
>> plot(t,sin(t-pi/2),'--mo')
>> plot(t,sin(t-pi),':bs')
>> hold off
属性设置
>> figure % 生成新的绘图窗口
>> plot(t,sin(2*t),'-mo',...
'LineWidth',2,... % 设置曲线粗细
'MarkerEdgeColor','k',... % 设置数据点边界颜色
'MarkerFaceColor',[.49 1 .63],... % 设置填充颜色,三原色的位置,0可以不打的
'MarkerSize',12) % 设置数据点型大小
3、坐标轴设置
(1)常用的坐标控制命令
>> x = 0:.025:pi/2;
plot(x,tan(x),'-ro')
>> axis([0 pi/2 0 5])
(2)轴控制指令
采用多子图表现时,图形形状不仅受“控制指令”的影响,而且受整个图面“宽高比”及“子图数目”的影响。
>> clear
>> t=0:2*pi/99:2*pi;
x=1.15*cos(t);y=3.25*sin(t); % y为长轴,x为短轴
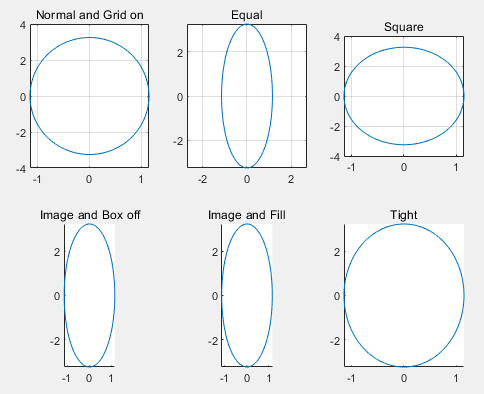
>> subplot(2,3,1),plot(x,y),axis normal,grid on, %grid on 设置网格线
title('Normal and Grid on')
>> subplot(2,3,2),plot(x,y),axis equal,grid on,title('Equal') %坐标轴长度相等
>> subplot(2,3,3),plot(x,y),axis square,grid on,title('Square') %绘图外面的框是正方形
>> subplot(2,3,4),plot(x,y),axis image,box off,title('Image and Box off')
>> subplot(2,3,5),plot(x,y),axis image fill,box off
title('Image and Fill')
>> subplot(2,3,6),plot(x,y),axis tight,box off,title('Tight')
(3)坐标轴标签设置
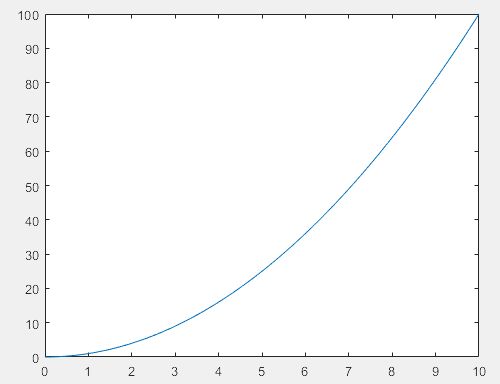
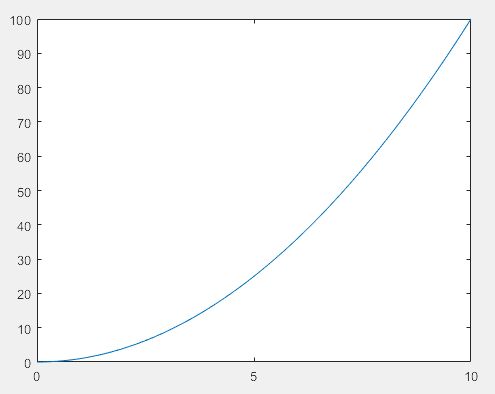
>> x = linspace(0,10); % 0到10之间均匀取数
y = x.^2;
plot(x,y)
>> xticks([0 5 10])
>> xticklabels({'x = 0','x = 5','x = 10'})
>> xticklabels({'0天','5天','10天'})
>> grid on%画分网格线
>> clear
>> figure
>> t = 0:pi/20:2*pi;
plot(t,sin(t),'-.r*')
>> hold on
>> plot(t,sin(t-pi/2),'--mo')
>> plot(t,sin(t-pi),':bs')
>> hold off
>> set(gca,'Xtick',[pi/2,pi,pi*3/2,2*pi],'Ytick', [-1,-0.5,0,0.5,1])
% gca:当前图形的句柄
>> set(gca,'XTickLabel',{'$$\frac{\pi}{2}$$','$$\pi$$','$$\frac{3\pi}{2}$$','$$2\pi$$'},'YTickLabel', {'-1','-0.5','0','0.5','1'},'TickLabelInterpreter','latex')
% TickLabelInterpreter 解析
(4)图形标识
>> clf
>> clear
>> t=0:pi/50:2*pi;
y=sin(t);plot(t,y);
axis([0,2*pi,-1.2,1.2])
>> text(pi/2,1.02,'\fontsize{16}\leftarrow\fontname {隶书}在\pi/2\fontname{隶书}处\itsin(t)\fontname{隶书}极大值')
% fontsize 字号
% leftarrow 左箭头
% fontname 字体
% it指的是斜体
![]()
(5)双坐标轴
>> x = 0:0.01:20; % x坐标
y1 = 200*exp(-0.05*x).*sin(x); % Y1
y2 = 0.8*exp(-0.5*x).*sin(10*x); % Y2
[AX,H1,H2] = plotyy(x,y1,x,y2,'plot'); % 绘制双坐标轴图形
set(get(AX(1),'Ylabel'),'String','Slow Decay') % 纵轴标签1
set(get(AX(2),'Ylabel'),'String','Fast Decay') % 纵轴标签2
xlabel('Time (\musec)') % x标签
title('Multiple Decay Rates') % 图形标题
set(H1,'LineStyle','--') % 线形1
set(H2,'LineStyle',':') % 线形2
![]()
R2016a之后新版方式
>> figure
yyaxis left
plot(x,y1,'--')
xlabel('Time (\musec)') % x标签
ylabel('Slow Decay')
yyaxis right
plot(x,y2,':')
ylabel('Slow Decay')
title('Multiple Decay Rates') % 图形标题
包括之后叠加新的曲线,只需要用上hold on命令就行,这种形式更方便
4、子图绘制
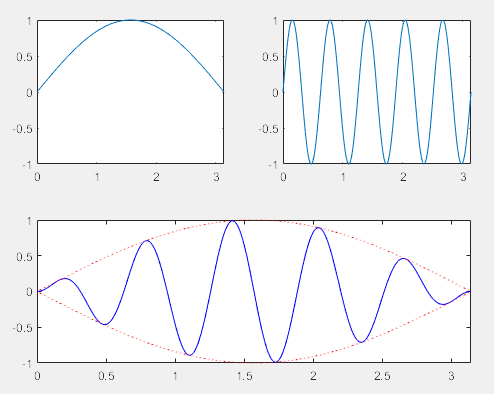
>> clf;clear
t=(pi*(0:1000)/1000)';
y1=sin(t);y2=sin(10*t);
y12=sin(t).*sin(10*t);
subplot(2,2,1)
plot(t,y1);
axis([0,pi,-1,1])
subplot(2,2,2) %注意:绘图的时候是按照行来排列1234的
plot(t,y2)
axis([0,pi,-1,1])
subplot(2,2,[3 4])
plot(t,y12,'b-',t,[y1,-y1],'r:')
axis([0,pi,-1,1])
% subplot('position',[0.2,0.05,0.6,0.45])
% 整个窗口左下角是(0,0),绘图的图片起点是(0.2,0.05)的位置
% 0.6表示的是宽度(即横轴长度),0.45表示的是长度(即纵轴长度)
5、二维图形
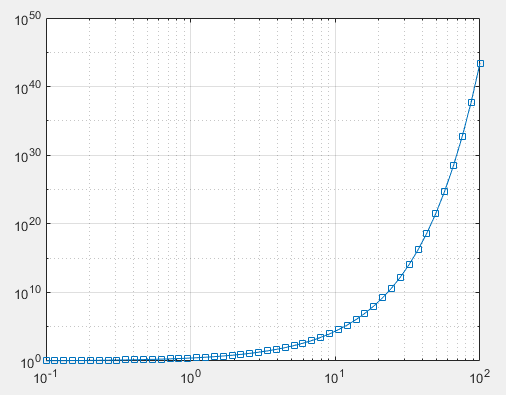
(1)双轴对数图形
>> x = logspace(-1,2); % 生成50个等对数间距的坐标
loglog(x,exp(x),'-s')
grid on
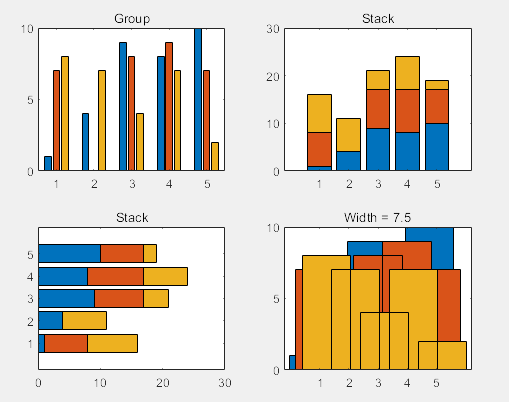
(2)条形图
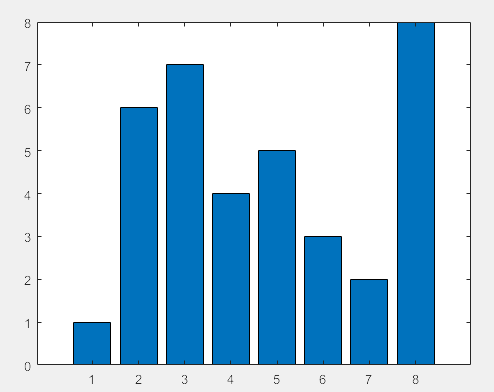
>> Y = round(rand(5,3)*10); %随机产生一个5×3矩阵,每个元素为1-10之间的整数
subplot(2,2,1) %设定绘图区域,在图形对象的左上角绘制
bar(Y,'group') %绘制纵向条形图
title 'Group' %添加标题Group
subplot(2,2,2) %在图形对象的右上角绘制
bar(Y,'stack')
title 'Stack'
subplot(2,2,3) %在图形对象的左下角绘制
barh(Y,'stack') %绘制横向条形图
title 'Stack'
subplot(2,2,4) %在图形对象的右下角绘制
bar(Y,7.5)
title 'Width = 7.5'
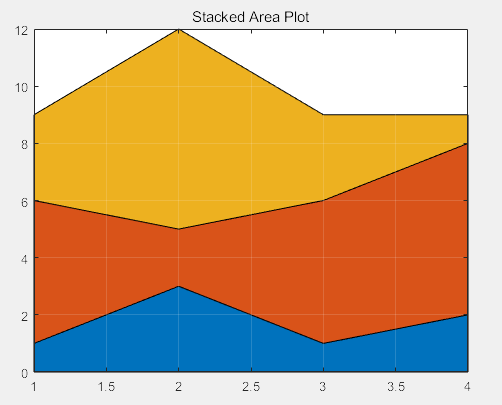
(3)区域图
>> figure %先画1312,然后画5256,向上叠加
Y = [1, 5, 3;
3, 2, 7;
1, 5, 3;
2, 6, 1];
area(Y)
grid on
set(gca,'Layer','top') % 将图纸的背景放到所画的图像的顶层
title 'Stacked Area Plot' % 图名
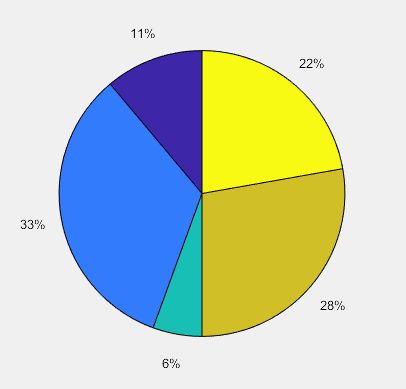
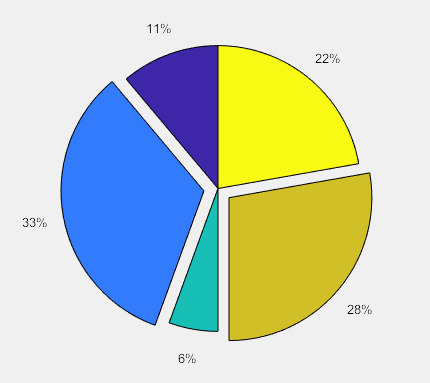
(4)饼形图
1)单个饼形图
>> X = [1 3 0.5 2.5 2];
pie(X)
>> explode = [0 1 0 1 0];
pie(X,explode)
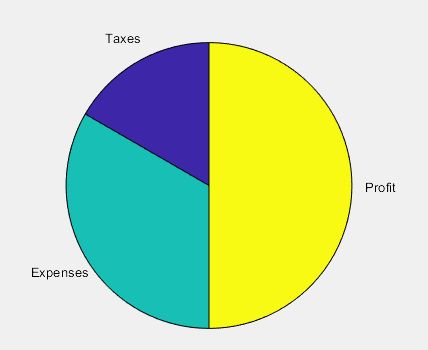
>> figure
X = 1:3;
labels = {'Taxes','Expenses','Profit'};
pie(X,labels)
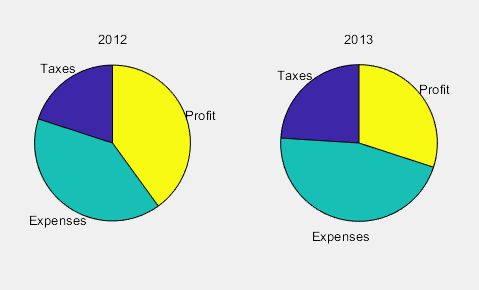
2)两个饼形图
>> X = [0.2 0.4 0.4];
labels = {'Taxes','Expenses','Profit'};
ax1 = subplot(1,2,1);
pie(ax1,X,labels)
title(ax1,'2012');
Y = [0.24 0.46 0.3];
ax2 = subplot(1,2,2);
pie(ax2,Y,labels)
title(ax2,'2013');
(5)直方图
>> figure
x = -4:0.1:4;
y = randn(10000,1); %生成一组符合正态分布的数
histogram(y,x) %绘制直方图
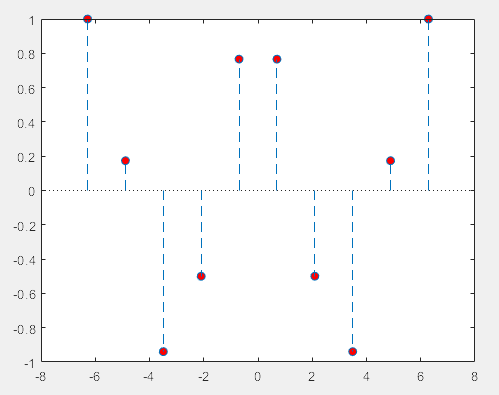
(6)stem杆图
>> figure
t = linspace(-2*pi,2*pi,10); % 创建10个位于-2*pi到2*pi之间的等间隔的数
h = stem(t,cos(t),'fill','--'); % 以'--'绘制离散数据图,fill表示给蓝色圆圈填充上颜色
set(get(h,'BaseLine'),'LineStyle',':') % 改变基准线的线型
set(h,'MarkerFaceColor','red') % 填充的内容为红色
(7)阶跃图形
x = linspace(-2*pi,2*pi,40); % 创建40个位于-2*pi到2*pi之间的等间隔的数
stairs(x,sin(x)) % 绘制正弦曲线的二维阶跃图形
![]()
(8)误差图
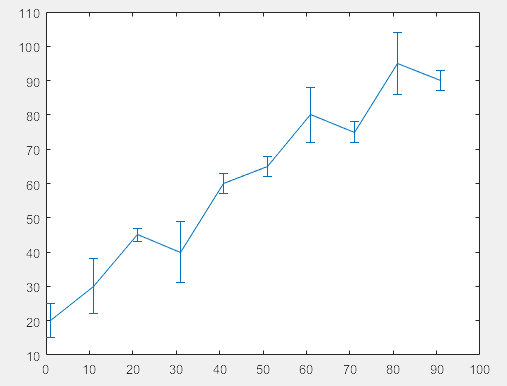
>> % 误差相同情况
x = 1:10:100;
y = [20 30 45 40 60 65 80 75 95 90];
err = 8*ones(size(y));
errorbar(x,y,err)
>> % 误差变化情况
x = 1:10:100;
y = [20 30 45 40 60 65 80 75 95 90];
err = [5 8 2 9 3 3 8 3 9 3];
errorbar(x,y,err)
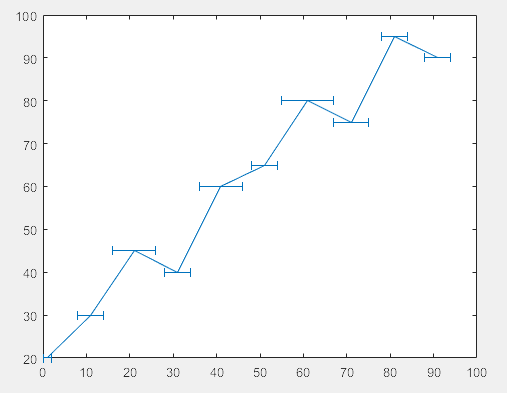
>> % 水平方向误差
x = 1:10:100;
y = [20 30 45 40 60 65 80 75 95 90];
err = [1 3 5 3 5 3 6 4 3 3];
errorbar(x,y,err,'horizontal')
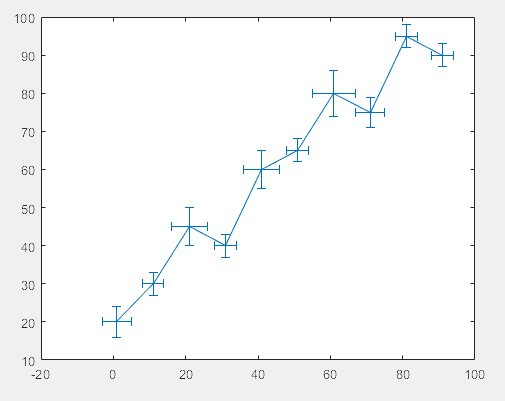
>> % 双方向误差
x = 1:10:100;
y = [20 30 45 40 60 65 80 75 95 90];
err = [4 3 5 3 5 3 6 4 3 3];
errorbar(x,y,err,'both')
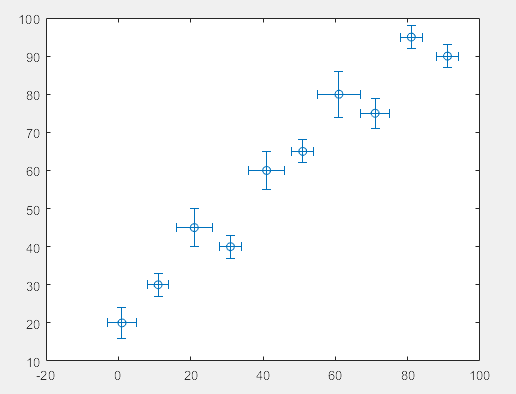
>> % 双方向误差,没有线情况
x = 1:10:100;
y = [20 30 45 40 60 65 80 75 95 90];
err = [4 3 5 3 5 3 6 4 3 3];
errorbar(x,y,err,'both','o')
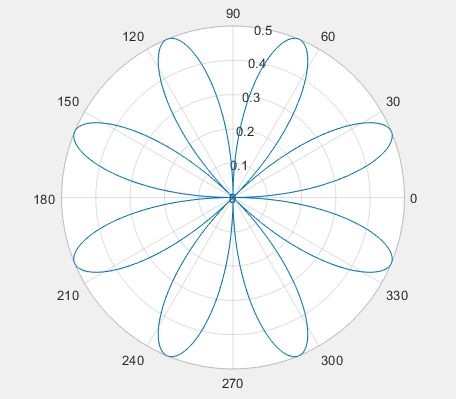
(9)极坐标图
>> theta = 0:0.01:2*pi; %角度
rho = sin(2*theta).*cos(2*theta);
polarplot(theta,rho)
6、三维图形
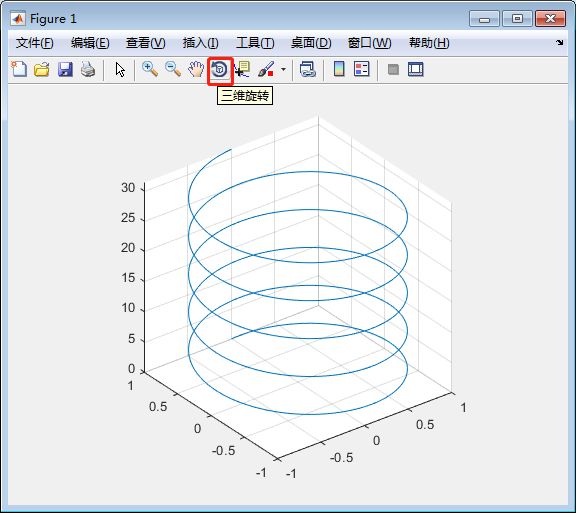
(1)三维曲线图
>> t = 0:pi/50:10*pi;
plot3(sin(t),cos(t),t)
grid on
axis square
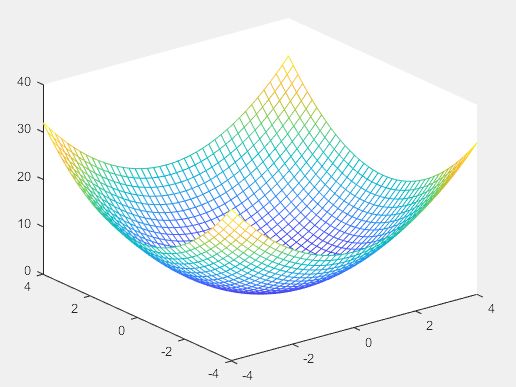
(2)绘制函数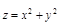 的网格图
的网格图
>> x=-4:.2:4;y=x; % x:1*41 y:1*41
[X,Y]=meshgrid(x,y); % X:41*41重复41行 Y:41*41 重复41列,将一维数据生成网格数据
Z=X.^2+Y.^2; %点乘,计算的是相对应的元素之间的计算
mesh(X,Y,Z) %绘制网格图
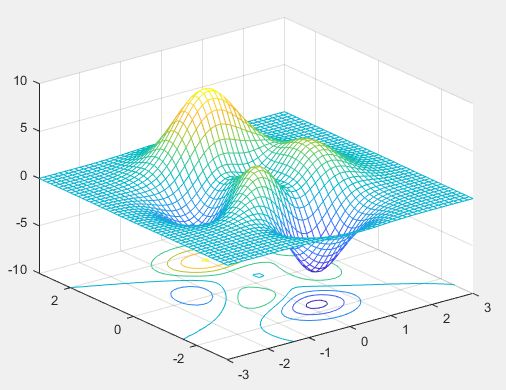
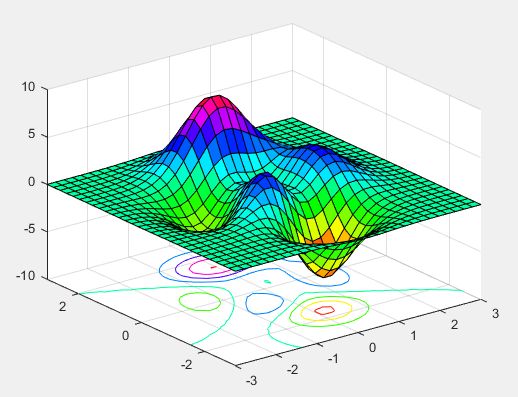
(3)绘制peaks函数的三维网格图及其在底面投影的等高线图
>> [X,Y] = meshgrid(-3:.125:3);
Z = peaks(X,Y);
meshc(X,Y,Z); % 绘制网格图的同时,在底面加上等高线图
axis([-3 3 -3 3 -10 10])
(4)曲面图
>> [X,Y,Z] = peaks(30);
surfc(X,Y,Z) %绘制曲面,加上等高线
colormap hsv %设置颜色
axis([-3 3 -3 3 -10 10])
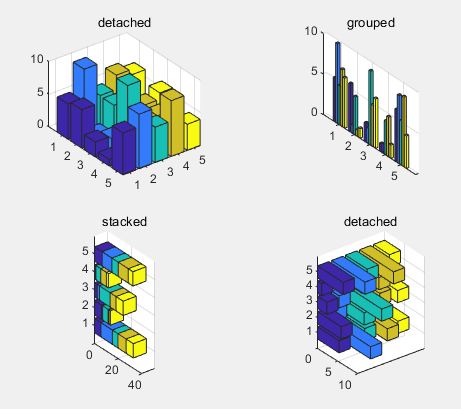
(5)三维柱状图
>> X=rand(5,5)*10; % 产生5×5矩阵,其中每个元素为1~10之间的随机数
subplot(221),bar3(X,'detached'),title('detached');
subplot(222),bar3(X,'grouped'),title('grouped');
subplot(223),bar3h(X,'stacked'),title('stacked');
subplot(224),bar3h(X,'detached'),title('detached');
三维柱状图可能看起来更好看,但是会挡住后面数据的展示
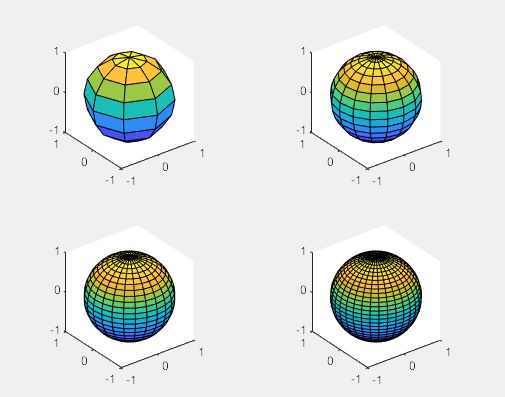
(6)三维球体图
>> figure
subplot(2,2,1)
sphere(8) % 括号中的数字指生成球体的面数,这里是指8×8
axis equal
subplot(2,2,2)
sphere(16)
axis equal
subplot(2,2,3)
sphere(24)
axis equal
subplot(2,2,4)
sphere(32)
axis equal
(7)三维饼形图
>> figure
x = 1:3;
labels = {'Taxes','Expenses','Profit'};
explode=[0 1 0 ] % 突出显示向量x的第二个元素
pie3(x,explode,labels)
explode =
0 1 0
(8)三维等高线图
>> [X,Y] = meshgrid([-2:.25:2]); % 生成维数相同的两个矩阵X,Y
Z = X.*exp(-X.^2-Y.^2);
contour3(X,Y,Z,40) % 绘制Z的等高线,40为等高线的数目
surface(X,Y,Z,'EdgeColor',[.8 .8 .8],'FaceColor','none') % 绘制表面图
grid off % 去掉网格线
view(-15,25) % 设定视角
colormap cool % 建立颜色图
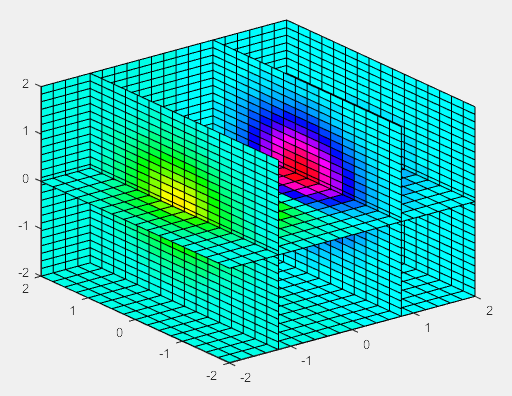
(9)三维切片图
绘制x,y,z在 [-2,2]范围内的![]() 函数的分布(此时有四个维度,切出一个面来展示)
函数的分布(此时有四个维度,切出一个面来展示)
>> figure
[x,y,z] = meshgrid(-2:.2:2,-2:.25:2,-2:.16:2);
v = x.*exp(-x.^2-y.^2-z.^2);
xslice = [-1.2,.8,2];
yslice = 2;
zslice = [-2,0];
slice(x,y,z,v,xslice,yslice,zslice)
colormap hsv
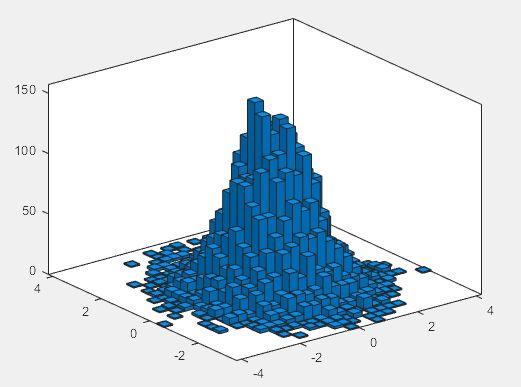
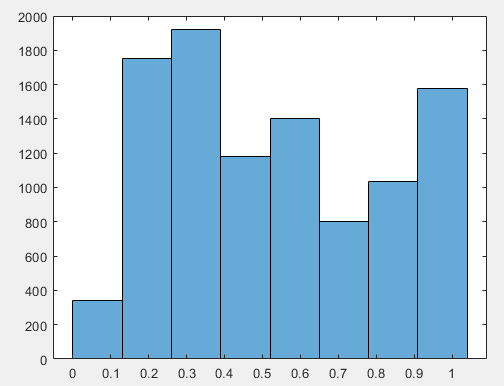
(10)三维直方图
>> figure
x = randn(10000,1);
y = randn(10000,1);
h = histogram2(x,y)
h =
Histogram2 - 属性:
Data: [10000×2 double]
Values: [28×26 double]
NumBins: [28 26]
XBinEdges: [1×29 double]
YBinEdges: [1×27 double]
BinWidth: [0.3000 0.3000]
Normalization: 'count'
FaceColor: 'auto'
EdgeColor: [0.1500 0.1500 0.1500]
显示 所有属性
(11)视点控制
>> [X,Y,Z] = peaks(30);
subplot(121),surf(X,Y,Z)
view(3) % 默认的三维视角
subplot(122),surfc(X,Y,Z)
view(30,60) % 和x轴夹角为30度,和y轴夹角为60度
(12)光照控制
>> figure
[X,Y,Z] = peaks(30);
surfc(X,Y,Z)
colormap hsv
axis([-3 3 -3 3 -10 10])
light('Position',[-20,20,5]) % 光照控制,数字指的是角度
第2节 图形句柄(handle)
1、图形对象基本概念
Matlab的图形系统是面向对象的,图形对象之间的关系为父代与子代的关系。
MATLAB图形对象包括:
每个图形对象都拥有自己的句柄 ( handle )。所有能创建图形对象的matlab函数都可给出所创建图形对象的句柄。
Root 是关联计算机屏幕的一个图形对象。Matlab系统只有一个Root对象,它没有父对象,子对象是Figure。当启动Matlab时,Root对象就创建,用户无法再创建一个Root,也无法删除这个对象。
图形对象举例:
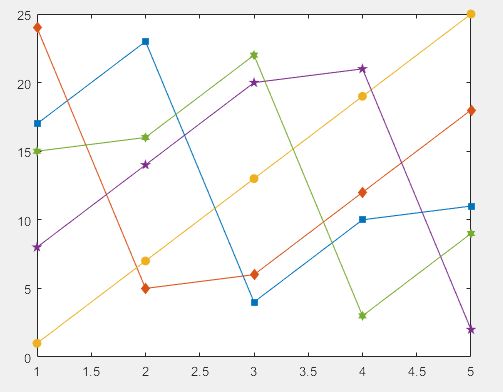
>> plot(rand(5)) %生成五条任意的折线
>> ax = gca %返回当前轴对象的句柄
ax =
Axes - 属性:
XLim: [1 5] % x轴范围
YLim: [0 1]
XScale: 'linear' %线型
YScale: 'linear'
GridLineStyle: '-'
Position: [0.1300 0.1100 0.7750 0.8150] %(0,0)位置,宽度以及高度
Units: 'normalized' % 单位:归一化
>> ax.Children %查看子对象
ans =
5×1 Line 数组:
Line
Line
Line
Line
Line
>> ax.Parent %查看父对象
ans =
Figure (1) - 属性:
Number: 1
Name: ''
Color: [0.9400 0.9400 0.9400]
Position: [403 246 560 420]
Units: 'pixels' %单位:像素
>> af=gcf %返回当前窗口对象的句柄
af =
Figure (1) - 属性:
Number: 1
Name: ''
Color: [0.9400 0.9400 0.9400]
Position: [403 246 560 420]
Units: 'pixels'
>> af.Parent % 即根对象:显示器的屏幕
ans =
Graphics Root - 属性:
CurrentFigure: [1×1 Figure]
ScreenPixelsPerInch: 96
ScreenSize: [1 1 1366 768]
MonitorPositions: [1 1 1366 768]
Units: 'pixels'
还可以指定父对象,比如上面图中可以将画的线组成一个群组对象
>> close all
>> clear
>> figure
>> hg = hggroup;
>> plot(rand(5),'Parent',hg)
>> ax = gca
ax =
Axes - 属性:
XLim: [1 5]
YLim: [0 1]
XScale: 'linear'
YScale: 'linear'
GridLineStyle: '-'
Position: [0.1300 0.1100 0.7750 0.8150]
Units: 'normalized'
显示 所有属性
>> ax.Children
ans =
Group - 属性:
Children: [5×1 Line]
Visible: 'on'
HitTest: 'on'
显示 所有属性
>> ax.Children.Children
ans =
5×1 Line 数组:
Line
Line
Line
Line
Line
MATLAB在用户调用绘图命令时总会创建一个轴和图形对象。在用户创建一个图形M文件的时候,尤其是别人在使用用户创建的程序时,最好使用命令来设置轴和图形对象。进行此设置可以解决如下两个问题。
(1)用户的M文件绘制的图形覆盖了当前图形窗口(用户单击图形窗口,该窗口就会变为当前窗口)。
(2)当前图形或许处于一种意外的状态,并没有像程序设置的那样显示。
专用函数
| gcf | 返回当前窗口对象的句柄 | Get Current Figure |
|---|---|---|
| gca | 返回当前轴对象的句柄 | Get Current Axes |
| gco | 返回当前图形对象的句柄 | Get Current Object |
句柄属性的设置与修改
| get | 获得句柄图形对象的属性和返回某些对象的句柄值 |
|---|---|
| set | 改变图形对象的属性 |
| delete(h) | 删除句柄为h的图形对象 |
| 直接通过属性赋值来修改 |
>> get(0) %% 获取显示器属性
CallbackObject: [0×0 GraphicsPlaceholder]
Children: [1×1 Figure]
CurrentFigure: [1×1 Figure]
FixedWidthFontName: 'SimHei'
HandleVisibility: 'on'
MonitorPositions: [1 1 1366 768]
Parent: [0×0 GraphicsPlaceholder]
PointerLocation: [390 57]
ScreenDepth: 32
ScreenPixelsPerInch: 96
ScreenSize: [1 1 1366 768]
ShowHiddenHandles: 'off'
Tag: ''
Type: 'root'
Units: 'pixels'
UserData: []
>> set(gca,'YAxisLocation','right') %将轴对象的Y轴改到右边
>> plot(rand(5))
ax = gca
>> ax.YAxisLocation='left'
>> ax.YAxisLocation='Right'
2、图形窗口设置
(1)图像窗口(Figure)
Figure对象是Matlab系统中显示的图形窗口。用户可建立任意多个Figure窗口。所有Figure对象的父对象都是Root对象,而其他所有Matlab图形对象都是Figure的子对象。
- figure( ) 创建图形窗口
- close( ) 删除图形窗口
- clf( ) 图形图形窗口中的子对象
- gcf 返回当前窗口对象的句柄
(2)创建图形窗口 :figure
- figure 利用缺省属性值来创建新的图形窗口对象。
- figure(‘PropertyName’,propertyvalue,…) 利用指定的属性值来创建图形窗口对象。对于用户没有显式地定义的属性值,将其设置为默认的属性值。
- figure(h) 如果句柄h所指示的图形窗口对象存在,则将其设置为当前窗口,并将其移动到屏幕的最前方。如果h所指示的图形窗口不存在且h是个整数 (h >= 1),则创建一个图形窗口,并将窗口的句柄设置为h;如果h不是整数,则返回错误信息。
- h = figure(…) 返回图形窗口对象的句柄。
备注:为了在一个已有的图形窗口中绘制图形,这个窗口必须是激活的,或者是当前的图形窗口。
>> T=datetime(2018,1,1:10,0,0,0);
>> for n=1:10
figure('Name',datestr(T(n),'yyyy年mm月dd日'),'NumberTitle','off',...
'Position',[200+n*30 250-n*20 560 420]);
% 注意,这里的位置是适用于双显示器且主显示器在左方情况,测试时需要相应修改
% datestr 将日期的变量转换为年月日的格式
% 'NumberTitle','off',将标题的编号关闭掉
plot(T(n)+hours(0:23),sin(1:24)*n)
ylim([-10,10])
end
>> hold on %在当前点击的窗口上进行增加绘图
plot(T(n)+hours(0:23),cos(1:24)*n)
>> findobj %查找对象函数
ans =
28×1 graphics 数组:
Root
Figure (3: 2018年01月03日)
Figure (2: 2018年01月02日)
Figure (4: 2018年01月04日)
Figure (5: 2018年01月05日)
Figure (6: 2018年01月06日)
Figure (7: 2018年01月07日)
Figure (8: 2018年01月08日)
Figure (10: 2018年01月10日)
Figure (9: 2018年01月09日)
Axes
Axes
Axes
Axes
Axes
Axes
Axes
Axes
Axes
Line
Line
Line
Line
Line
Line
Line
Line
Line
(3)删除图形窗口:close
- close 删除当前figure,相当于close(gcf)
- close(h) 删除由h确定的figure。如果h是一个向量或矩阵,就删除由h指定的所有图像
- close name 删除指定名称的figure
- close all 删除所有句柄没有隐藏的figure
- close all hidden 删除所有figure,包括句柄隐藏的。
- status = close(…) 如果指定的figure已经被删除则返回1,否则为0。
(4)清除图形窗口中的子对象:clf
- clf 删除当前图形窗口中、句柄未被隐藏(即它们的HandleVisibility属性为on)的图形对象。
- clf(‘reset’) 或 clf reset 删除当前图形窗口中的所有图形对象,无论其句柄是否被隐藏,同时将图形窗口的属性(除Position, Units, PaperPosition, PaperUnits外)恢复为默认值。
- clf(fig)或 clf(fig,‘reset’) 清除由句柄为fig的图形窗口中的内容。
- figure_handle = clf(…) 返回图形窗口的句柄。
(5)坐标轴 (axes)
- axes( ) 创建坐标轴
- cla 清除坐标轴中的子对象
- gca 返回当前轴对象的句柄
- xlim( ) / ylim( ) / zlim( ) 设置x / y / z 轴刻度范围
- grid 设置坐标轴网格线的显示
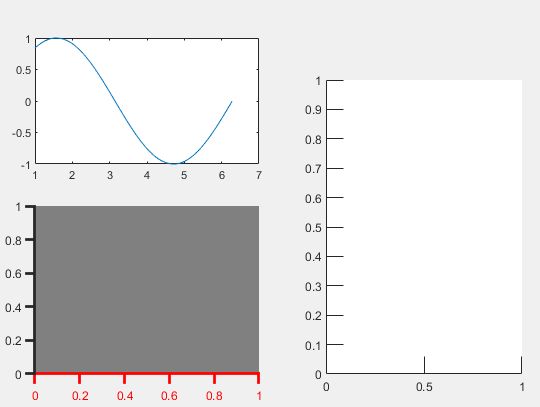
>> figure
h1 = axes('position',[0.08,0.1,0.4,0.4])
h2 = axes('position',[0.6,0.1,0.35,0.7])
h3 = axes('position',[0.08,0.6,0.4,0.3])
set(h1,'Color',[0.5,0.5,0.5],'XColor',[1,0,0],'LineWidth',2)
% 区域颜色设置为灰色,X轴颜色设置为红色,线宽改为2
set(h1,'TickDir','out','TickLength',[0.04,0.03])
% 刻度线朝外,并且变长
set(h2,'TickLength',[0.06,0.02])
plot(h3,1:0.01:2*pi,sin(1:0.01:2*pi))
h1 =
Axes - 属性:
XLim: [0 1]
YLim: [0 1]
XScale: 'linear'
YScale: 'linear'
GridLineStyle: '-'
Position: [0.0800 0.1000 0.4000 0.4000]
Units: 'normalized'
显示 所有属性
h2 =
Axes - 属性:
XLim: [0 1]
YLim: [0 1]
XScale: 'linear'
YScale: 'linear'
GridLineStyle: '-'
Position: [0.6000 0.1000 0.3500 0.7000]
Units: 'normalized'
显示 所有属性
h3 =
Axes - 属性:
XLim: [0 1]
YLim: [0 1]
XScale: 'linear'
YScale: 'linear'
GridLineStyle: '-'
Position: [0.0800 0.6000 0.4000 0.3000]
Units: 'normalized'
显示 所有属性
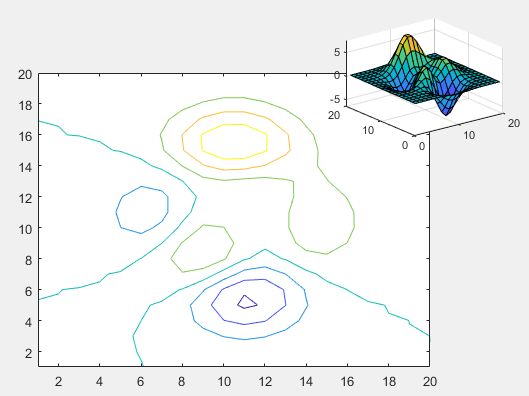
(6)图形叠加
figure
ax1 = axes('Position',[0.1 0.1 0.7 0.7]);
ax2 = axes('Position',[0.65 0.65 0.28 0.28]);
contour(ax1,peaks(20))
surf(ax2,peaks(20))
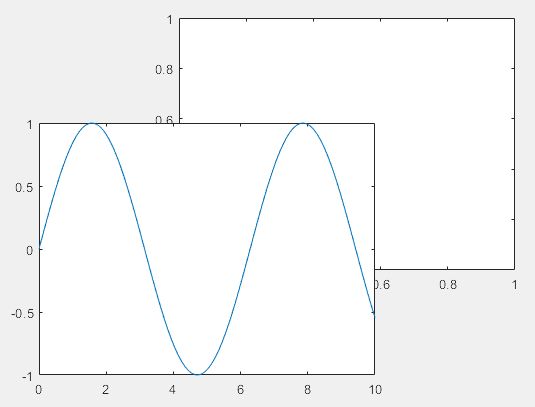
>> figure
ax1 = axes('Position',[0.1 0.1 .6 .6],'Box','on');
ax2 = axes('Position',[.35 .35 .6 .6],'Box','on');
axes(ax1) % 将第一个窗口置于前方
x = linspace(0,10);
y = sin(x);
plot(x,y)
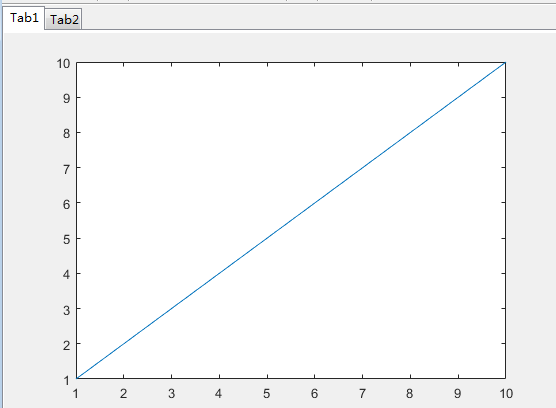
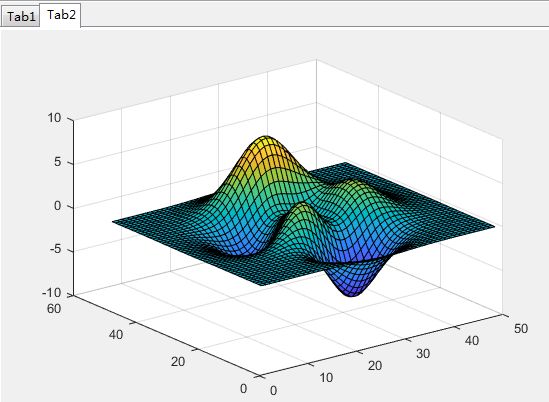
(7)tab页中创建新图形
>> figure
tab1 = uitab('Title','Tab1');
ax1 = axes(tab1);
plot(ax1,1:10)
tab2 = uitab('Title','Tab2');
ax2 = axes(tab2);
surf(ax2,peaks)
3、图形对象设置
(1)子图所对应的对象
>> clear
>> close all
>> t=(pi*(0:1000)/1000)';
y1=sin(t);y2=sin(10*t);
y12=sin(t).*sin(10*t);
subplot(2,2,1)
plot(t,y1);
axis([0,pi,-1,1])
subplot(2,2,2)
plot(t,y2)
axis([0,pi,-1,1])
% subplot('position',[0.2,0.05,0.6,0.45])
subplot(2,2,[3 4])
plot(t,y12,'b-',t,[y1,-y1],'r:')
axis([0,pi,-1,1])
>> A=findobj
A =
10×1 graphics 数组:
Root
Figure (1)
Axes
Axes
Axes
Line
Line
Line
Line
Line
>> A(2)
ans =
Figure (1) - 属性:
Number: 1
Name: ''
Color: [0.9400 0.9400 0.9400]
Position: [403 246 560 420]
Units: 'pixels'
显示 所有属性
>> A(2).Children
ans =
3×1 Axes 数组:
Axes
Axes
Axes
>> A(3)
ans =
Axes - 属性:
XLim: [0 3.1416]
YLim: [-1 1]
XScale: 'linear'
YScale: 'linear'
GridLineStyle: '-'
Position: [0.1300 0.1100 0.7750 0.3412]
Units: 'normalized'
显示 所有属性
>> A(3).Children
ans =
3×1 Line 数组:
Line
Line
Line
(2)设置已有图形对象属性
>> figure
h = plot(magic(5));
>> set(h,'Marker','s','MarkerFaceColor','g') %给图形数据点加上标记并设置颜色
%设置标记点为方块形状,并设置标记点内部的颜色
![]()
如果用户需要为每条线添加不同的标记符号,同时将标记符号的颜色设置为线的颜色,则需要定义两个元胞数组,一个储存属性名,另一个储存需要设置的属性值。
比如可以设置元胞数组prop_name储存有两个元素:
>> prop_name(1) = {'Marker'};
prop_name(2) = {'MarkerFaceColor'};
另外元胞数组prop_values储存有10个值:5个用来指定标记的形状,另外5个用来指定颜色属性。需要注意的是:prop_values是一个二维元胞数组,第1维表示h中的哪个句柄,第2维表示哪一个属性。
>> prop_values(1,1) = {'s'}; % 标记形状
prop_values(1,2) = {get(h(1),'Color')}; % 获取线的颜色
prop_values(2,1) = {'d'};
prop_values(2,2) = {get(h(2),'Color')};
prop_values(3,1) = {'o'};
prop_values(3,2) = {get(h(3),'Color')};
prop_values(4,1) = {'p'};
prop_values(4,2) = {get(h(4),'Color')};
prop_values(5,1) = {'h'};
prop_values(5,2) = {get(h(5),'Color')};
在定义了以上两个元胞数组之后,接下来调用set函数将对象设置为新的属性:
>> set(h,prop_name,prop_values)
4、轴对象设置
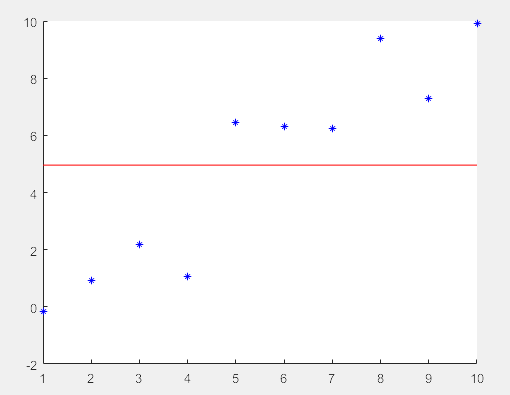
% 创建一个.m文件
function myfunc(x)
y = 1.5*cos(x) + 6*exp(-.1*x) + exp(.07*x).*sin(3*x);
ym = mean(y); % 求平均值
hfig = figure('Name','Function and Mean',...
'Pointer','crosshair'); % 设置窗口名和指针
% 鼠标放置到图形窗口,会变成十字形
hax = axes('Parent',hfig); %创建轴对象
plot(hax,x,y)
hold on
plot(hax,[min(x) max(x)],[ym ym],'Color','red')
hold off
ylab = get(hax,'YTick'); % 提取出y轴有的数值标签
set(hax,'YTick',sort([ylab ym])) % 设置轴对象 将平均数放置到数组里面,sort排序,从大到小
title ('y = 1.5cos(x) + 6e^{-0.1x} + e^{0.07x}sin(3x)') % 标题
xlabel('X Axis'); ylabel('Y Axis') % 坐标轴标签
%最终可以在Y轴显示出平均数值
>> x = -10:.005:40;
>> myfunc(x)
5、弹出式菜单
>> figure
% 定义弹出式菜单
cmenu = uicontextmenu;
% 画正弦曲线,并把弹出式菜单与正弦曲线联系起来
x=-2*pi:pi/100:2*pi;
y=sin(x);
hline = plot(x,y, 'UIContextMenu', cmenu);
title('使用不同线型绘制正弦曲线')
%定义弹出式菜单子菜单项的“callback”属性值。
cb1 = ['set(hline, ''LineStyle'', ''--'')'];
% 单引号里面再放引号,就必须放双引号了
cb2 = ['set(hline, ''LineStyle'', '':'')'];
cb3 = ['set(hline, ''LineStyle'', ''-'')'];
% 定义弹出式菜单的子菜单项
item1 = uimenu(cmenu, 'Label', 'dashed', 'Callback', cb1);
item2 = uimenu(cmenu, 'Label', 'dotted', 'Callback', cb2);
item3 = uimenu(cmenu, 'Label', 'solid', 'Callback', cb3);
% 右击曲线,会出现dashed,dotted,solid三个按钮,点击之后,会改变线型
按钮
>> figure
% uicontrol,加控件
% pushbutton 普通按钮
% Callback 按下按钮后会执行什么操作
h = uicontrol('Style', 'pushbutton', 'String', '绘图',...
'Position', [20 150 100 70], 'Callback', 'plot(0:0.01:2*pi,sin(0:0.01:2*pi))');
% 点击绘图按钮之后,将会生成函数
6、坐标轴关联
>> figure
ax1 = subplot(2,2,1);
x1 = linspace(0,6);
y1 = sin(x1);
plot(x1,y1)
ax2 = subplot(2,2,2);
x2 = linspace(0,10);
y2 = sin(2*x2);
plot(x2,y2)
ax3 = subplot(2,2,[3,4]);
x3 = linspace(0,16);
y3 = sin(6*x3);
plot(x3,y3)
linkaxes([ax1,ax2,ax3],'xy')%让三幅图的xy轴进行联动,也可以只写x或者y
% 点击图片中的放大镜,三个图片是一起动的
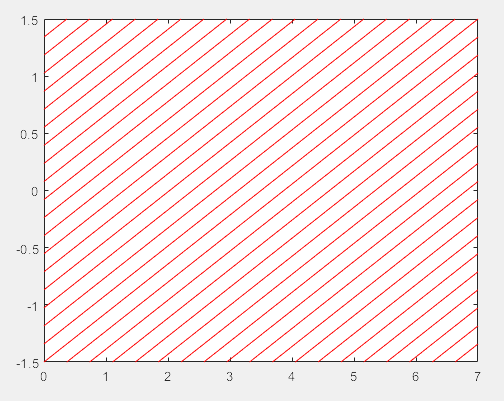
7、阴影底纹的复杂绘图
>> x=linspace(0,2*pi,100); % 曲线数据,x坐标
y1=sin(x); % 曲线数据,y坐标
y2=cos(x); % 曲线数据,y坐标
>> % 绘制斜线底纹
N=20; % 绘制斜线的密度
a=linspace(-1.5,1.5,N); % 斜线的顶点坐标
b=linspace(0,7,N); % 斜线的顶点坐标
plot([zeros(1,N);b],fliplr([a;ones(1,N)*1.5]),'r') % 绘制最底层斜线(上三角)
>> hold on
plot([b;ones(1,N)*7],fliplr([ones(1,N)*-1.5;a]),'r') % 绘制最底层斜线(下三角)
>> % 计算区域数据
Y1=max(y1,y2);
Y2=min(y1,y2);
Ymax=repmat(1.5,1,length(Y1))-Y1;
Ymin=repmat(-1.5,1,length(Y1));
Ydown=Y2-Ymin;
Yup=Y1-Y2;
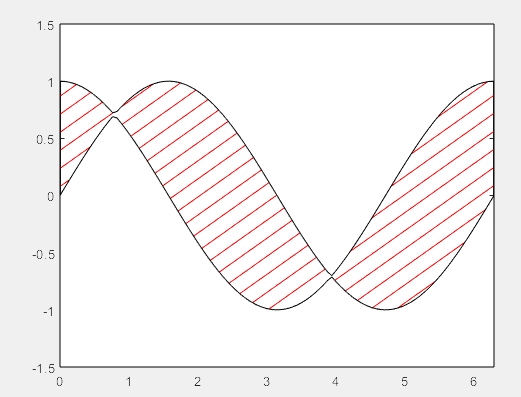
>> % 绘制区域图,覆盖掉原来的底纹
h=area(x,[Ymin;Ydown;Yup;Ymax]',-1.5)
h(1).FaceColor = 'w';% 不需要的区域该为白色,看起来像是没有东西
h(2).FaceColor = 'w';% 不需要的区域该为白色,看起来像是没有东西
h(3).FaceAlpha=0;% 需要显示底纹的区域该为透明,露出最底层的斜线
h(4).FaceColor = 'w';% 不需要的区域该为白色,看起来像是没有东西
xlim([0,2*pi])% 更改坐标,去掉多余的图
h =
1×4 Area 数组:
Area Area Area Area
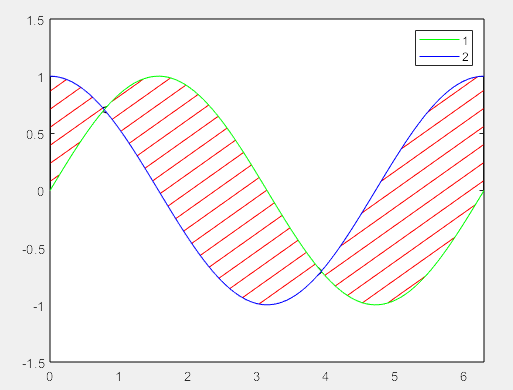
>> hh=plot(x,y1,'g',x,y2,'b') % 最终在绘制原始边界曲线,覆盖掉原来的曲线,更直接,并可设置颜色
% legend 如果直接用legend的话会有太多的标签
legend(hh,'1','2') % 只给指定曲线加标签
hh =
2×1 Line 数组:
Line
Line
第三章 MATLAB流程结构、脚本文件、函数文件的编写
第1节 流程控制
1、脚本文件和函数文件
(1)示例脚本文件(Ex1.m)
a=2;
b=2;
clf;
x=-a:0.2:a;y=-b:0.2:b;
z=zeros(20,10);
for i=1:length(y)
for j=1:length(x)
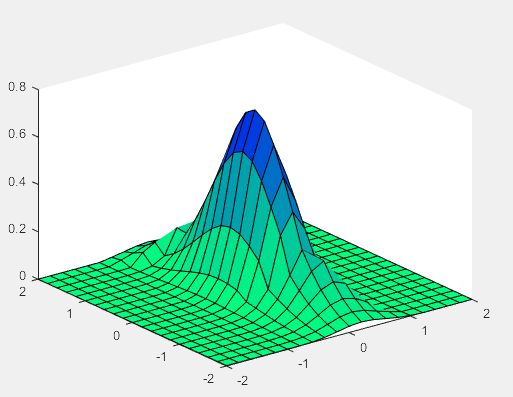
if x(j)+y(i)>1
z(i,j)=0.5457*exp(-0.75*y(i)^2-3.75*x(j)^2-1.5*x(j));
elseif x(j)+y(i)<=-1
z(i,j)=0.5457*exp(-0.75*y(i)^2-3.75*x(j)^2+1.5*x(j));
else
z(i,j)=0.7575*exp(-y(i)^2-6.*x(j)^2);
end
end
end
axis([-a,a,-b,b,min(min(z)),max(max(z))]);
colormap(flipud(winter));
surf(x,y,z);
(2)示例函数文件(fact.m)
function f = fact(n) % 函数定义行,脚本式M文件无此行
% Compute a factorial value. % H1 行,会在详细信息中展示,表名函数是干什么的
% FACT(N) returns the factorial of N, % Help 文本
% usually denoted by N!
% Put simply, FACT(N) is PROD(1:N). % 注释
f = prod(1:n); % 函数或脚本主体
- 在脚本里可以多次调用函数文件
- 保存的时候函数名和文件名一定要一样
2、顺序结构
%Ex2.m
a=1;
b=2;
c=3;
ans1=a+b;
ans2=a*b;
ans3=ans2*ans1-c;
f = fact(5); % 调用fact函数
% 命令窗口中也可运行
>> Ex2 正确
>> Ex2.m 错误
3、条件语句
(1)if语句
% Ex3.m if…end
a=8; %需要改值的时候
if rem(a, 2) == 0 % 判断a是否是偶数
disp('a is even')
b = a/2
end
% Ex4.m if…else…end
a=4
b=4
if a>b
disp('a is bigger than b') % 若a>b则执行此句
y=a; % 若a>b则执行此句
else
disp('a is not bigger than b') % 若a<=b则执行此句
y=b; % 若a<=b则执行此句
end
% Ex5.m if…elseif…else…end
n=5
if n < 0 % 如果n是负数,则显示错误信息
disp('Input must be positive');
elseif rem(n,2) == 0 % 如果n是偶数,则除以2
A = n/2;
else
A = (n+1)/2; % 如果n是奇数,则加1,然后除以2
end
A
if n < 0 % 如果n是负数,则显示错误信息
disp('Input must be positive');
else %一般换行会自动缩进,或者右击,智能缩进
if rem(n,2) == 0 % 如果n是偶数,则除以2
A = n/2;
else
A = (n+1)/2; % 如果n是奇数,则加1,然后除以2
end
end
A
(2)switch语句
%Ex6.m
switch 开关语句
case 条件语句1
执行语句1
case 条件语句2
执行语句2
…
otherwise
执行语句n
end
V=6;
switch V
case 1 % 判断var是不是1
disp('1')
case {2,3,4} % 判断var是不是2,3,4
disp('2 or 3 or 4')
case 5 % 判断var是不是5
disp('5')
otherwise % 其他情况
disp('something else')
end
4、循环语句
(1)for循环
-
variable表示变量,initval:stepval:endval表示一个以initval开始,以endval结束,步长为stepval的向量。
-
其中initval、stepval和endval可以是整数、小数或负数。
-
但是当initval
endval时,stepval则必须为小于0的数。 -
表达式也可以为initval:endval这样的形式,此时,stepval的默认值为1,initval必须小于endval。
-
另外还可以直接将一个向量赋值给variable,此时程序进行多次循环直至穷尽该向量的每一个值。
for variable = initval:stepval:endval
statement1
...
statementn
end
% 可行的表达方式
for n=1:2:100
for n=1:100
for n=10:-1:1
for n=[1 3 4 5]
a=1:0.1:10
for n=1:90
N=a(n)
% Ex7.m
x=ones(1,6)
for n = 2:6 % 循环控制
% n=5 在循环变量中,通过改变变量值,不能改变循环次数,但是可以改变计算结果
x(n) = 2 * x(n - 1); % 循环体
end
x
>> Ex7
x =
1 1 1 1 1 1
x =
1 2 4 8 16 32
for m = 1:5
for n = 1:10
A(m, n) = 1/(m + n - 1) ; % 使用循环体给变量A赋值
n %中间加变量可以看出循环进行到哪一步了
end
m
end
A
(2)while循环
while循环的判断控制是逻辑判断语句,因此,它的循环次数并不确定。
(多数while循环和for循环是可以互相改变的,尽量用for循环,不容易变成死循环)
while 表达式
执行语句
end
在这个循环中,只要表达式的值不为false,程序就会一直运行下去。通常在执行语句中要有使表达式值改变的语句。用户必须注意的是:当程序设计出了问题,比如表达式的值总是true时,程序就容易陷入死循环。
% Ex8.m
i=1;
while i<10 % i小于10时进行循环
x(i)=i^3; % 循环体内的计算
i=i+1; % 表达式值的改变 (一定要写改变循环变量的语句)
end
x
% ctrl+c 退出死循环
>> Ex8
x =
1 8 27 64 125 216 343 512 729
% Ex9.m 多种循环体的嵌套使用
clear
clc
for i=1:1:6 % 行号循环,从1到6
j=6;
while j>0 % 列号循环,从6到1
x(i,j)=i-j; % 矩阵x的第i行第j列元素值为其行列号的差
if x(i,j)<0 % 当x(i,j)为负数时,取其相反数
x(i,j)=-x(i,j);
end
j=j-1;
end
end
x
x =
0 1 2 3 4 5
1 0 1 2 3 4
2 1 0 1 2 3
3 2 1 0 1 2
4 3 2 1 0 1
5 4 3 2 1 0
5、continue和break命令
(1)continue命令
continue命令经常与for或while循环语句一起使用,作用是结束本次循环,即跳过循环体中下面尚未执行的语句,接着进行下一次循环。
% Ex10.m
fid = fopen('magic.m','r'); % 打开魔方矩阵函数文件,存入文件句柄fid,r:只读
%可以右击magic.m,查看这个函数文件
count = 0;
while ~feof(fid) % 判断是否到了文件的结尾,end of file ,读取文件是一行一行读取
line = fgetl(fid); % 读取一行文件内容
line(line==' ')=[]; % 删除空格
if isempty(line) || strncmp(line,'%',1) || ~ischar(line) % || 表示或
% 判断是否是空行与注释
continue % 如果是注释或者空行,则进入下一轮while循环,而不会记录行数
end
count = count + 1; % 记录行数
end
fprintf('%d lines\n',count); % 输出结果
fclose(fid); % 关闭文件
>> Ex10
27 lines
(2)break命令
语句break通常用在循环语句或条件语句中。通过使用break语句,可以不必等待循环的自然结束,而可以根据循环的终止条件来跳出循环。(并不只是退出这一次循环,是退出当前这个循环语句)
% Ex11.m
fid = fopen('fft.m','r');
s = '';
while ~feof(fid)
line = fgetl(fid);
% 如果遇到空行,则使用break命令跳出while循环
if isempty(line) || ~ischar(line)
break
end
s = sprintf('%s%s\n', s, line); % 将非空行内容写入s
end
disp(s); % 显示结果
fclose(fid);
6、return命令
使用return命令,能够使得当前正在调用的函数正常退出。首先对特定条件进行判断,然后根据需要,调用return语句终止当前运行的函数。
% Ex_return.m
function d = Ex_return(A)
% Ex_return用来演示return命令的使用
if isempty(A)
disp('输入为空阵');
return
d=0;
else
d=sin(A);
end
>> Ex_return([])
输入为空阵
>> d=Ex_return([])
输入为空阵
调用 "Ex_return" 时,未对输出参数 "d" (可能还包括其他参数)赋值。
% 因为return会跳出整个函数,并不会执行d=0
>> d=Ex_return(pi/2)
d =
1
7、人机交互命令
- 输入提示----input
- 键盘控制-----keyboard
- 暂停-------pause
%Ex12.m
reply = input('Do you want more? Y/N [Y]: ', 's'); %s:字符串类型
if reply == 'Y'
disp('Welcome to the MATLAB world !');
else
keyboard % 在程序中控制是不是进入调试模式
disp('Goodbye.')
end
>> Ex12
Do you want more? Y/N [Y]: Y
Welcome to the MATLAB world !
>> Ex12
Do you want more? Y/N [Y]: N
K>> a=1
a =
1
K>> reply
reply =
'N'
K>> dbcont %退出当前调试模式,但是会直接运行完下面的程序
Goodbye.
>> Ex12
Do you want more? Y/N [Y]: N
K>> dbquit %直接退出整个函数,不会执行后面的程序了
%Ex13.m
t = 0:pi/20:2*pi;
for k = 1:.1:10
y = exp(sin(t.*k));
h = plot(t,y);
% drawnow; 在每一次循环中进行实时的绘图,而不会跳过中间的执行过程,只显示最后的结果
% pause(0.2) 每次暂停,都只暂停0.2秒
pause %可以细看怎么画图的,如果不加pause,只显示最终结果,会把开始的给覆盖掉
end
8、函数的类型
(1)主函数
function d = Ex_return(A)
% Ex_return用来演示return命令的使用
if isempty(A)
disp('输入为空阵');
return
d=0;
else
d=sin(A);
end
(2)子函数
一个M文件中可以写入多个函数定义式,排在第1个位置的是主函数,排在主函数后面进行定义的函数都叫子函数,子函数的排列无规定顺序。子函数只能被同一个文件上的主函数或其他子函数调用
注意:几个子函数虽然在同一个文件上,但各有自己的变量存储空间,子函数之间不能相互存取别人的变量。
[avg, med] = newstats(u) % 主函数
从一个M文件中调用函数时,MATLAB首先查看被调用的函数是否是本M文件上的子函数,是,则调用它;不是,再寻找是否有同名的私有函数;如果还不是,则从搜索路径中查找其他M文件。因为最先查找的是子函数,所以在M文件中可以编写子函数来覆盖原有的其他同名函数文件。
例如【newstats】中子函数名称mean和median是MATLAB内建函数,但是通过子函数的定义,我们可以调用自定义的mean和median函数。
function [avg, med] = newstats(u) % 主函数
% NEWSTATS Find mean and median with internal functions.
n = length(u);
avg = mean(u, n); %系统中也有mean函数,会优先调用子函数
med = median(u, n); % 求中位数
end %function和end是对应的,要么所有函数都加end,要么都不加
function a = mean(v, n) % 子函数,子函数的n和主函数的n并不一样
% Calculate average.
a = sum(v)/n;
end
function m = median(v, n) % 子函数
% Calculate median.
w = sort(v);
if rem(n, 2) == 1
m = w((n+1) / 2);
else
m = (w(n/2) + w(n/2+1)) / 2;
end
end
(3)私有函数
- 私有函数编写形式上和主函数是相同的,但它是私有的,实际上是另一种子函数,只有父M文件函数能调用它。
- 私有函数的存储需要在当前目录下建一个子目录,子目录名字必须为private。
- 存放于private文件夹内的函数即为私有函数,它的上层目录称为父目录,只有父目录中的M文件才可以调用该私有函数。
- 私有函数对于其父目录以外的目录中的M文件来说是不可见的。
- 调用私有函数的M文件必须在private子目录的直接父目录内。
- 私有函数只能被其父文件夹中的函数调用,因此,用户可以开发自己的函数库,函数名称可以与系统标准M函数库名称相同,而不必担心在函数调用时发生冲突,因为MATLAB首先查找私有函数,然后再查找标准函数。
(4)嵌套函数
% 最简单的嵌套函数的结构如下:
function x = A(p1, p2)
...
function y = B(p3)
...
end
...
end
% 另外一个主函数还可以嵌套多个函数,例如多个平行嵌套函数结构如下:
function x = A(p1, p2)
...
function y = B(p3)
...
end
function z = C(p4)
...
end
...
end
% 多层嵌套函数
function x = A(p1, p2)
...
function y = B(p3)
...
function z = C(p4)
...
end
...
end
...
end
(5)匿名函数
- 匿名函数提供了一种不需要每次都调用M文件编辑器的快速建立简单函数的方法。用户可以在MATLAB命令行、函数文件或脚本文件中建立匿名函数。
- 匿名函数总体来讲比较简单,由一条表达式组成,能够接受多个输入或输出参数。使用匿名函数可以避免文件的管理和存储。但是匿名函数的执行效率比较低,会占用较多的时间。
>> sqr = @(x) x.^2; % 创建匿名函数句柄
>> a=sqr(5) % 函数句柄的调用
a =
25
>> A=7;
B=3;
sumAxBy = @(x, y) (A*x + B*y); % 创建匿名函数
sumAxBy(5, 7) % 函数句柄的调用
ans =
56
- 匿名函数数组
>> A = {@(x)x.^2, @(y)y+10, @(x,y)x.^2+y+10}
A =
1×3 cell 数组
{@(x)x.^2} {@(y)y+10} {@(x,y)x.^2+y+10}
>> A{1}(4) + A{2}(7)
ans =
33
% 4*4+7+10=33
(6)函数句柄
函数句柄是一种数据结构,用来存储函数。例如,可以使用函数句柄用来创建匿名函数,或者通过函数句柄将一个函数传递给另一个函数。
>> y=@sin; % 创建函数句柄
z=y(pi/2) % 调用函数句柄
z =
1
>> f = @(X)find(X); % find用来查找矩阵中的非0元素
m = [3 2 0; -5 0 7; 0 0 1]
[row col val] = f(m)
m =
3 2 0
-5 0 7
0 0 1
row =
1
2
1
2
3
col =
1
1
2
3
3
val =
3
-5
2
7
1
>> plot(0:0.05:1,humps)
h = @humps; % 创建函数句柄h
x = fminbnd(h, 0.3, 1) % 将函数句柄传递给优化函数
% fminbnd函数用来求解标量最小值优化问题,采用的是黄金分割法和抛物内插法
x =
0.6370
第2节 变量调试模式
1、局部变量
每个函数都有自己的局部变量,这些变量存储在该函数独立的工作空间中,与其他函数的变量及主工作空间中的变量分开存储。当函数调用结束时,这些变量随之删除,不保存在内存中。并且除了函数返回值,该函数不改变工作空间中其他变量的值。
% zrf_v.m 计算标准差
function f=zrf_v(x) %这个x就是局部变量
l=length(x);
s=sum(x);
y=s/l;
% t=zrf_fun(x,y);
t=zrf_fun(y);
f=sqrt(t/(l-1));
% function f=zrf_fun(x,y)
function f=zrf_fun(y)
%nested function
t=0;
for i=1:length(x) %嵌套函数是可以和父函数共享变量的
t=t+((x(i)-y).^2);
end
f=t;
end
end
>> a = randperm(100,50)
a =
1 至 13 列
46 21 93 18 71 34 97 66 47 81 6 50 89
14 至 26 列
80 40 51 99 54 83 39 22 7 67 98 3 92
27 至 39 列
12 13 32 42 4 70 30 91 84 72 94 57 77
40 至 50 列
53 62 27 25 56 49 36 75 64 86 38
>> f = zrf_v(a)
f =
28.6694
>> std(a) %计算标准差函数
ans =
28.6694
选中对应堆栈,可以查看临时变量
2、全局变量
全局变量可以在定义该变量的全部工作空间中有效。当在一个工作空间内改变该变量的值时,该变量在其他工作空间中的变量同时改变。
% countGlobalx.m
function countGlobalx(val)
global x %声明全局变量
if isempty(x)
x=val;
else
x = x+val;
end
% getGlobalx.m
function r = getGlobalx
global x
r = x;
>> countGlobalx(4) % 更改x的值
>> getGlobalx % 读取x的值
ans =
4
>>countGlobalx(6)
>> getGlobalx
ans =
10
>> clear global x % 清除全局变量
>> getGlobalx
ans =
[]
注意:使用全局变量有一定的风险,容易造成错误,所以建议用户尽量少使用全局变量。例如,用户可能不经意间在一个函数文件中声明的全局变量名和另外一个函数文件中的全局变量名相同,这样在运行程序的时候,一个函数就可能对另一个函数中使用的全局变量进行覆盖赋值,这种错误是很难被发现的。
3、程序调试
和其他编程语言一样,当使用MATLAB编写函数或者脚本M文件的时候,遇到错误(bug)是在所难免的,尤其是在比较大规模或者多人合作的情况下。因此,掌握程序调试的方法和技巧,对提高工作效率是很重要的。
一般来讲,程序代码的错误主要分为语法错误和逻辑错误两种。其中,语法错误通常包括变量名和函数名的误写、标点符号的缺漏和end等关键词的漏写等。对于这类错误,MATLAB会在编译运行时发现,并给出错误信息。用户很容易发现这类错误。而且与逻辑错误相比,这种错误也是比较容易修改的。
对于逻辑错误,情况相对而言比较复杂,处理起来也比较困难。其主要原因如下:逻辑错误一般会涉及算法模型与程序模型是否一致,还涉及编程人员对程序算法的理解是否正确,对MATLAB语言和机理的理解是否深入。逻辑错误的表现形态也比较多,如程序运行正常,但是结果异常,或者程序代码不能正常运行而中断等。逻辑错误相对于语法错误而言,更难查找错误原因,此时就需要使用工具来帮助完成程序的调试和优化。
- 1.设置断点
- 2.清除断点
- 3.恢复执行
- 4.切换工作空间
- 5.step,step in,step out
% debugEx1.m
% l = [ 2 3 1 2 4 ]; % x每个元素重复的个数
% v = [ 4 5 6 7 8 ]; % x中重复元素的值
% 求x = [ 4 4 5 5 5 6 7 7 8 8 8 8 ]
%% 错误方式
% clc
% clear
% l = [ 2 3 1 2 4 ]; % x每个元素重复的个数
% v = [ 4 5 6 7 8 ] % x中重复元素的值
% x=zeros(1,sum(l));
% i=1;
% while i<=sum(l)
% if l(1)>0
% x(i)=v(1);
% end
% l(1)=l(1)-1;
% if l(1)==0
% l(1)=[];
% v(1)=[];
% end
% i=i+1;
% end
%
% x
v =
4 5 6 7 8
x =
4 4 5 5 5 6 0 0 0 0 0 0
% 可以看到大概在i=7左右,出现了错误
% 在断点处右击——>设置条件断点——>i==5——>出现黄色断点——>运行,直接到第5次循环,并步进,可以发现会退出while循环
% 因为l一直在-1,所以sum(l)也一直在变化,并不是一直都是12
%% 正确方式
clear
clc
l = [ 2 3 1 2 4 ] % x每个元素重复的个数
v = [ 4 5 6 7 8 ] % x中重复元素的值
x=zeros(1,sum(l));
i=1;
l1=l;
while i<=sum(l1)
if l(1)>0
x(i)=v(1);
end
l(1)=l(1)-1;
if l(1)==0
l(1)=[];
v(1)=[];
end
i=i+1;
end
x
% debugEx2.m
% l = [ 2 3 1 2 4 ]; % x每个元素重复的个数
% v = [ 4 5 6 7 8 ]; % x中重复元素的值
% 求x = [ 4 4 5 5 5 6 7 7 8 8 8 8 ]
%% 错误计算方式
% clear
I = [ 2 3 1 2 4 ] % x每个元素重复的个数
V = [ 4 5 6 7 8 ] % x中重复元素的值
X=[];
k=1;
a=0;
for i=1:5
a=a+I(i);
X(k:a)=V(i);
k=k+a;
end
X
>> debugEx2
I =
2 3 1 2 4
V =
4 5 6 7 8
X =
4 4 5 5 5
%% 正确计算方式
%
clc
clear
I = [ 2 3 1 2 4 ] % x每个元素重复的个数
V = [ 4 5 6 7 8 ] % x中重复元素的值
X=[];
k=1;
a=0;
for i=1:5
a=a+I(i);
X(k:a)=V(i);
k=1+a;
end
X
4、错误处理
% try…catch语句的一般调用语法如下:
try
statements
catch exception
statements
end
% Ex_try_catch.m
clear
N=6;
A=magic(5);
A_N=A(N,:)
>> Ex_try_catch
位置 1 的索引超出数组范围(不能超过 5)。
出错 Ex_try_catch (line 4)
A_N=A(N,:)
try
A_N=A(N,:) % 取A的第N行元素
catch
A_end=A(end,:) % 如果取A(N,:)出错,则改取A的最后一行
end
5、MATLAB的搜索顺序
在编程的过程中,MATLAB在运行的过程中如果遇到命令test_command,它将按照以下搜索顺序来检查输入命令的具体含义。了解MATLAB的搜索顺序和了解运算符的优先级顺序是同等重要的,建议熟记以下搜索顺序,以免在编程过程中遇到难以察觉的错误。
- (1)检查test_command是否是一个变量名,如果不是则执行下一步。
- (2)检查test_command是否是一个子函数,如果不是则执行下一步。
- (3)检查test_command是否是一个私有函数,如果不是则执行下一步。
- (4)检查test_command是否是一个类构造器,如果不是则执行下一步。
- (5)检查test_command是否是一个重载函数,如果不是则执行下一步。
- (6)检查test_command是否是当前目录下的M文件,如果不是则执行下一步。
- (7)检查test_command是否是MATLAB搜索目录下的M文件或者MATLAB内建函数(built-in function),如果不是则执行下一步。
- (8)如果经过以上步骤还是找不到test_command的话,那么MATLAB将给出错误信息。
比如,创建一个变量名mean = 2,调用mean(5),会报错,因为这是个变量名,所以不要用函数名来命名变量,这样的话,函数就不能用了。
>> a = six
未定义函数或变量 'six'。
第四章 MATLAB数据分析及各种算法介绍
第1节 数据拟合
1、拟合函数
(1)多项式拟合
m是人为决定的,a值是需要选取的,最终要让误差最小,即最小二乘拟合
案例1:
>> x=1:1:10;
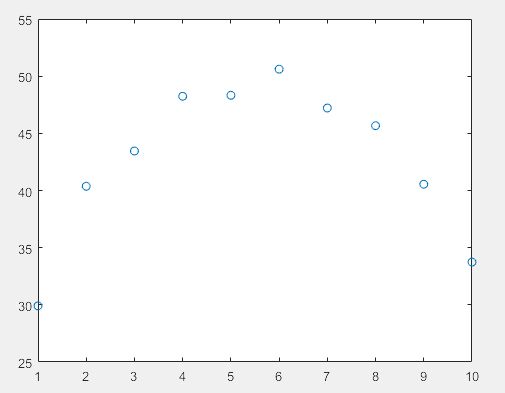
y=-0.9*x.^2+10*x+20+rand(1,10).*5; % 产生测试数据
plot(x,y,'o') % 绘图并标出原始数据点
>> p=polyfit(x,y,2) % 2次方是抛物线
p =
-0.8618 9.7580 22.3182 % 分别为x^2,x,常数项 的系数
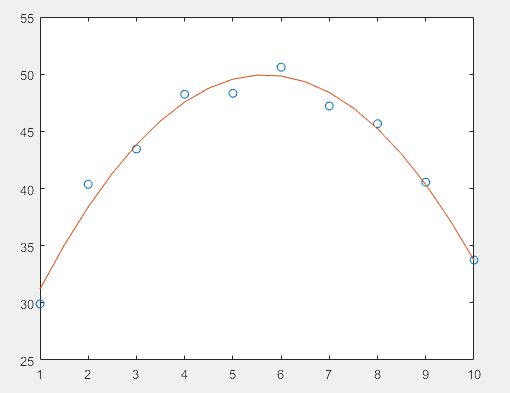
>> xi=1:0.5:10;
yi=polyval(p,xi); % 计算拟合的结果
hold on
plot(xi,yi); % 绘制拟合结果图
hold off
- 得到的p值和原始数据很相近
- 得到的p值和原始数据有差别,这是随机数造成的误差
- 在实际中是否可以消除这种误差,不可以期望通过算法来消除误差,要通过减少原始测量误差来实现
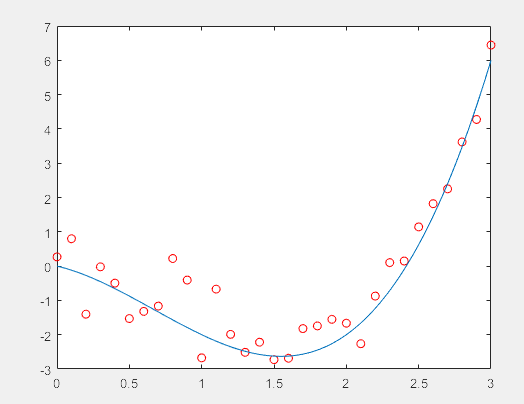
案例2:
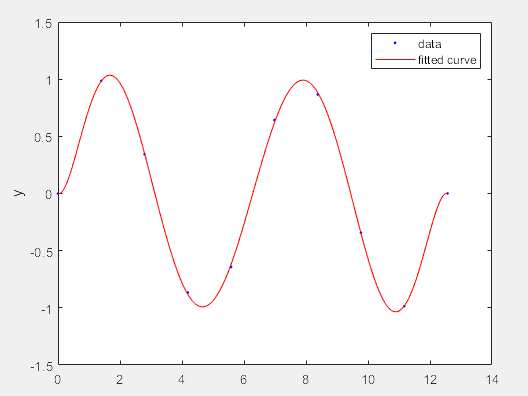
>> x = linspace(0,4*pi,10)';
y = sin(x);
p = polyfit(x,y,7);
x1 = linspace(0,4*pi);
y1 = polyval(p,x1);
figure
plot(x,y,'o')
hold on
plot(x1,y1)
hold off
案例3:预测
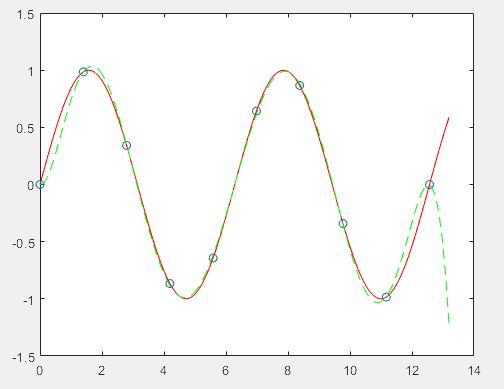
预测,看之后某些点的走向
绿色是预测,其实效果并不是很好
>> x2=linspace(0,4.2*pi,120);
y2=sin(x2);
x3=x2;
y3=polyval(p,x3);
figure
plot(x,y,'o')
hold on
plot(x2,y2,'r')
plot(x3,y3,'--g')
hold off
(2)fit函数
1)一维多项式拟合(曲线)
>> clear
x = linspace(0,4*pi,10)';
y = sin(x);
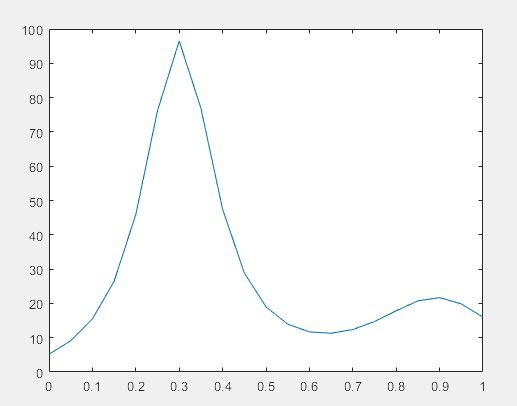
f=fit(x,y,'poly7') % 最大可到poly9,使用7阶多项式进行拟合
figure
plot(f,x,y)
f =
Linear model Poly7:
f(x) = p1*x^7 + p2*x^6 + p3*x^5 + p4*x^4 + p5*x^3 +
p6*x^2 + p7*x + p8
Coefficients (with 95% confidence bounds):
p1 = -6.261e-05 (-7.536e-05, -4.986e-05)
p2 = 0.002754 (0.002192, 0.003315)
p3 = -0.04638 (-0.05617, -0.0366)
p4 = 0.3702 (0.2847, 0.4556)
p5 = -1.381 (-1.77, -0.9917)
p6 = 1.908 (1.044, 2.772)
p7 = -0.1141 (-0.846, 0.6177)
p8 = 0.0001973 (-0.1321, 0.1325)
2)二维多项式拟合(曲面)
>> load franke % matlab自带的一组测试数据,包含x,y,z
>> sf = fit([x, y],z,'poly23') % 最大可到poly55,即x系数最大到5,y系数最大到5,ploy表示多项式系数
plot(sf,[x,y],z)
Linear model Poly23:
sf(x,y) = p00 + p10*x + p01*y + p20*x^2 + p11*x*y + p02*y^2 + p21*x^2*y
+ p12*x*y^2 + p03*y^3
Coefficients (with 95% confidence bounds):
p00 = 1.118 (0.9149, 1.321)
p10 = -0.0002941 (-0.000502, -8.623e-05)
p01 = 1.533 (0.7032, 2.364)
p20 = -1.966e-08 (-7.084e-08, 3.152e-08)
p11 = 0.0003427 (-0.0001009, 0.0007863)
p02 = -6.951 (-8.421, -5.481)
p21 = 9.563e-08 (6.276e-09, 1.85e-07)
p12 = -0.0004401 (-0.0007082, -0.0001721)
p03 = 4.999 (4.082, 5.917)
3)指定拟合参数和类型
>> clear
load census % 生成一组测试数据,cdate和pop,各21个
plot(cdate,pop,'o')
fo = fitoptions('Method','NonlinearLeastSquares',... % 非线性最小二乘
'Lower',[0,0],...
'Upper',[Inf,max(cdate)],... % 范围
'StartPoint',[1 1]); % 搜索的起始点
ft = fittype('a*(x-b)^n','problem','n','options',fo);
% 指定多项式的类型,n是可变参数,求解的是a和b
[curve2,gof2] = fit(cdate,pop,ft,'problem',2) % a*(x-b)^2
[curve3,gof3] = fit(cdate,pop,ft,'problem',3)
hold on
plot(curve2,'m')
plot(curve3,'c')
legend('Data','n=2','n=3')
hold off
curve2 =
General model:
curve2(x) = a*(x-b)^n
Coefficients (with 95% confidence bounds):
a = 0.006092 (0.005743, 0.006441) % 后面是置信区间
b = 1789 (1784, 1793)
Problem parameters:
n = 2
gof2 =
包含以下字段的 struct:
sse: 246.1543
rsquare: 0.9980
dfe: 19
adjrsquare: 0.9979
rmse: 3.5994
curve3 =
General model:
curve3(x) = a*(x-b)^n
Coefficients (with 95% confidence bounds):
a = 1.359e-05 (1.245e-05, 1.474e-05)
b = 1725 (1718, 1731)
Problem parameters:
n = 3
gof3 =
包含以下字段的 struct:
sse: 232.0058
rsquare: 0.9981
dfe: 19
adjrsquare: 0.9980
rmse: 3.4944
4)定义函数,根据指定函数文件进行拟合
function y = piecewiseLine(x,a,b,c,d,k)
% PIECEWISELINE A line made of two pieces
% that is not continuous.
y = zeros(size(x));
% This example includes a for-loop and if statement
% purely for example purposes.
for i = 1:length(x)
if x(i) < k
y(i) = a + b.* x(i);
else
y(i) = c + d.* x(i);
end
end
end
>> x = [0.81;0.91;0.13;0.91;0.63;0.098;0.28;0.55;...
0.96;0.96;0.16;0.97;0.96];
y = [0.17;0.12;0.16;0.0035;0.37;0.082;0.34;0.56;...
0.15;-0.046;0.17;-0.091;-0.071];
ft = fittype( 'piecewiseLine( x, a, b, c, d, k )' )
ft =
General model:
ft(a,b,c,d,k,x) = piecewiseLine( x, a, b, c, d, k )
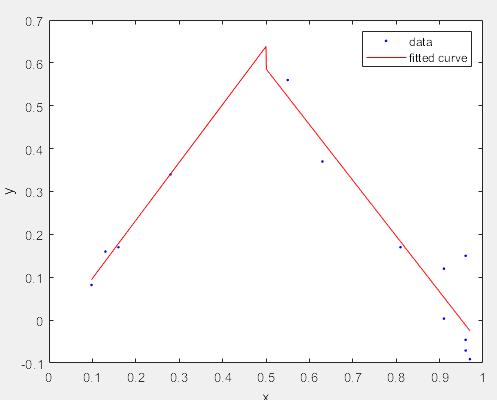
>> f = fit( x, y, ft, 'StartPoint', [1, 0, 1, 0, 0.5] ) % 起始点,abcdk初始分别为多少
f =
General model:
f(x) = piecewiseLine( x, a, b, c, d, k )
Coefficients (with 95% confidence bounds):
a = -0.03779
b = 1.352
c = 1.237
d = -1.301
k = 0.5
>> plot( f, x, y )
5)排除个别点之后进行拟合
>> clear
[x, y] = titanium; % x和y各生成49个数
>> gaussEqn = 'a*exp(-((x-b)/c)^2)+d'
startPoints = [1.5 900 10 0.6]
f1 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', [1 10 25]) %剔除第1,10,25个数
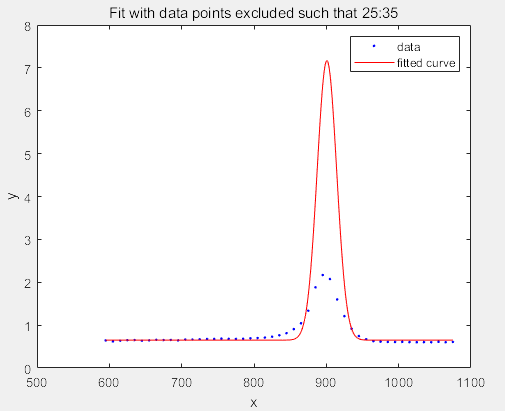
f2 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude', x < 800)
f3 = fit(x',y',gaussEqn,'Start', startPoints, 'Exclude',25:35)
% 剔除部分峰值,可以看出结果的变化
gaussEqn =
'a*exp(-((x-b)/c)^2)+d'
startPoints =
1.5000 900.0000 10.0000 0.6000
f1 =
General model:
f1(x) = a*exp(-((x-b)/c)^2)+d
Coefficients (with 95% confidence bounds):
a = 1.493 (1.432, 1.554)
b = 897.4 (896.5, 898.3)
c = 27.9 (26.55, 29.25)
d = 0.6519 (0.6367, 0.6672)
f2 =
General model:
f2(x) = a*exp(-((x-b)/c)^2)+d
Coefficients (with 95% confidence bounds):
a = 1.494 (1.41, 1.578)
b = 897.4 (896.2, 898.7)
c = 28.15 (26.22, 30.09)
d = 0.6466 (0.6169, 0.6764)
f3 =
General model:
f3(x) = a*exp(-((x-b)/c)^2)+d
Coefficients (with 95% confidence bounds):
a = 6.519 (-5.781e+04, 5.782e+04)
b = 900.8 (-6.541e+04, 6.721e+04)
c = 19.08 (-1.284e+04, 1.288e+04)
d = 0.6496 (0.6365, 0.6628)
>> x<800 % 显示的是逻辑数组
ans =
1×49 logical 数组
1 至 19 列
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
20 至 38 列
1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
39 至 49 列
0 0 0 0 0 0 0 0 0 0 0
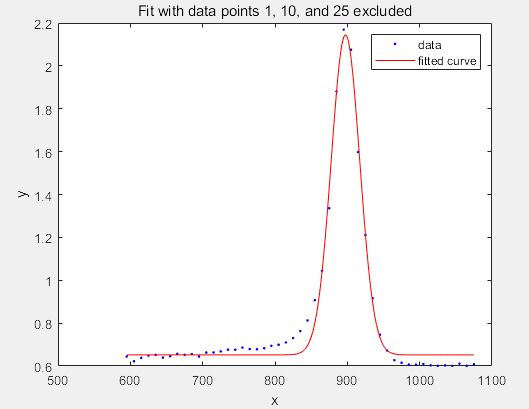
>> plot(f1,x,y)
title('Fit with data points 1, 10, and 25 excluded')
figure
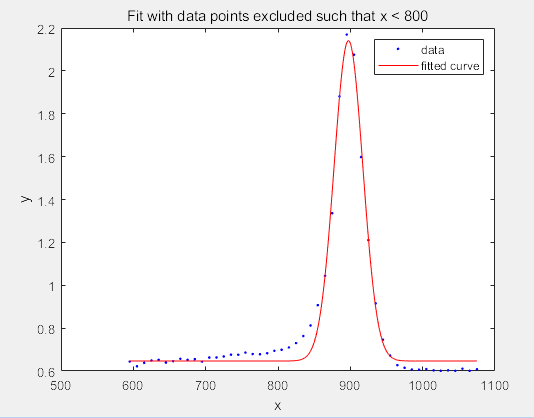
plot(f2,x,y)
title('Fit with data points excluded such that x < 800')
figure
plot(f3,x,y)
title('Fit with data points excluded such that 25:35')
% 注意y轴大小
6)曲面情况下剔除部分点,并在图中标记
>> clear
load franke
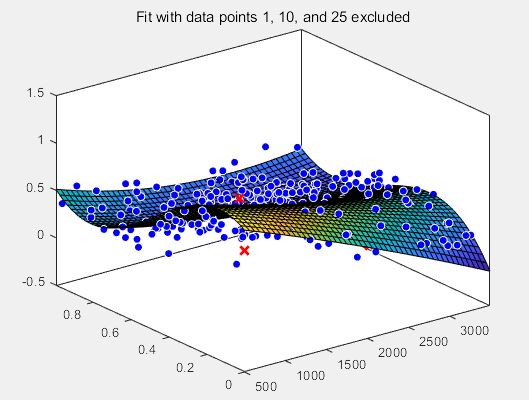
f1 = fit([x y],z,'poly23', 'Exclude', [1 10 25]);
f2 = fit([x y],z,'poly23', 'Exclude', z > 1);
figure
plot(f1, [x y], z, 'Exclude', [1 10 25]);
title('Fit with data points 1, 10, and 25 excluded')
figure
plot(f2, [x y], z, 'Exclude', z > 1);
title('Fit with data points excluded such that z > 1')
2、拟合工具 Curve Fitting app
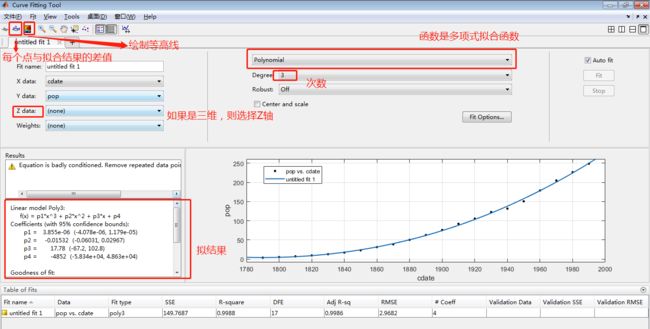
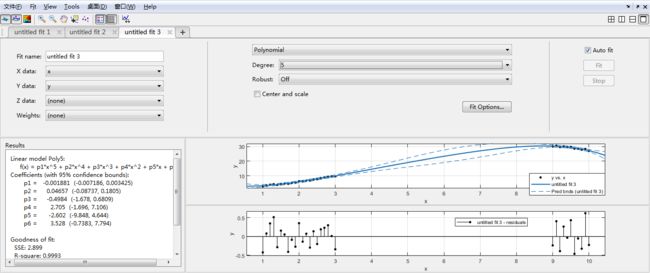
(1)介绍cftool
点击APP——>点击Curve Fitting
clear
load census % 输入测试数据,二维
>> load franke % 生成三维数据
Tools——>Exclude by Rule 剔除某些值
Tools——>Exclude Outliers 图上选取要剔除的值
(2)误差分析
>> clear
x = [1:0.1:3 9:0.1:10]';
c = [2.5 -0.5 1.3 -0.1];
y = c(1) + c(2)*x + c(3)*x.^2 + c(4)*x.^3 + (rand(size(x))-0.5);
Tools——>Prediction Bounds,选择置信区间,可以看出三阶的误差会比较小
3、数据平滑
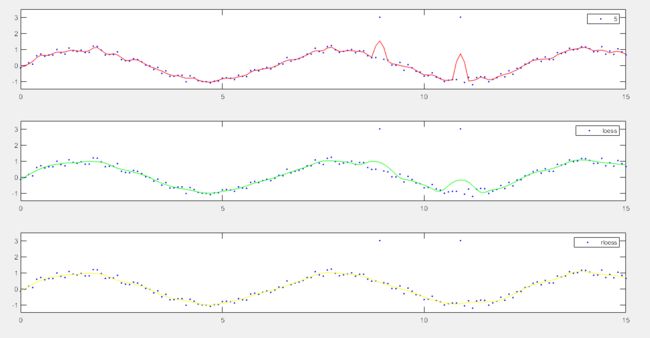
(1)滑动平均
>> clear
x = (0:0.1:15)';
y = sin(x) + 0.5*(rand(size(x))-0.5);
y([90,110]) = 3; % 第90和110个数改成3
yy0 = smooth(x,y,5); % 多少个数做平均,默认是5,一般放奇数
yy1 = smooth(x,y,0.1,'loess'); % 用10%的数据做平均,loess 线性最小二乘法
yy2 = smooth(x,y,0.1,'rloess');% 稳定模式的线性最小二乘
subplot(3,1,1)
plot(x,y,'b.',x,yy0,'r-')
set(gca,'YLim',[-1.5 3.5])
legend('5')
subplot(3,1,2)
plot(x,y,'b.',x,yy1,'g-')
set(gca,'YLim',[-1.5 3.5])
legend('loess') % Local regression
subplot(3,1,3)
plot(x,y,'b.',x,yy2,'y-')
set(gca,'YLim',[-1.5 3.5])
legend('rloess') % A robust version of 'lowess'
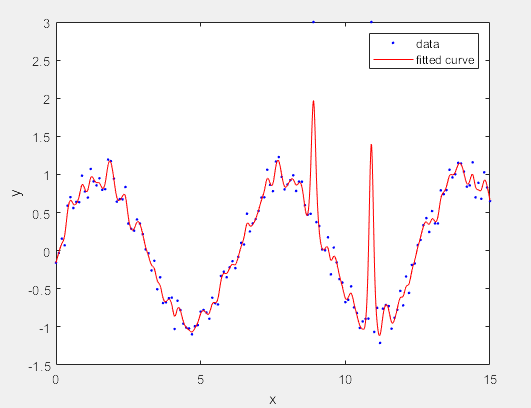
(2)平滑样条
p=0 最小二乘直线拟合
p=1 三次样条插值
>> f = fit(x,y,'smoothingspline');
figure
plot(f,x,y)
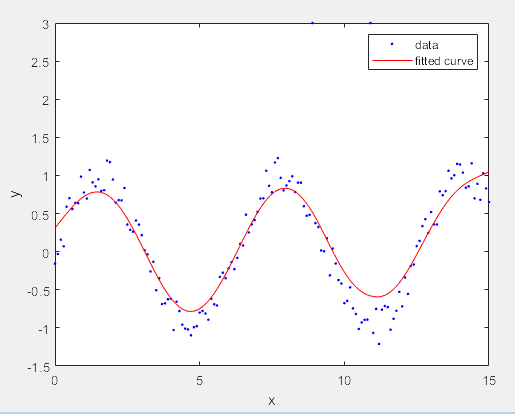
>> f = fit(x,y,'smoothingspline','SmoothingParam',0.4); % 更改P值
figure
plot(f,x,y)
>> [f,gof,out]= fit(x,y,'smoothingspline','SmoothingParam',0.4)
f =
Smoothing spline:
f(x) = piecewise polynomial computed from p
Coefficients:
p = coefficient structure
gof =
包含以下字段的 struct:
sse: 25.0266
rsquare: 0.7218
dfe: 141.4237
adjrsquare: 0.7049
rmse: 0.4207
out =
包含以下字段的 struct:
numobs: 151
numparam: 9.5763
residuals: [151×1 double]
Jacobian: []
exitflag: 1
p: 0.4000
>> options = fitoptions('Method','Smooth','SmoothingParam',0.3);
[f,gof,out] = fit(x,y,'smooth',options)
f =
Smoothing spline:
f(x) = piecewise polynomial computed from p
Coefficients:
p = coefficient structure
gof =
包含以下字段的 struct:
sse: 26.4747
rsquare: 0.7057
dfe: 142.3204
adjrsquare: 0.6898
rmse: 0.4313
out =
包含以下字段的 struct:
numobs: 151
numparam: 8.6796
residuals: [151×1 double]
Jacobian: []
exitflag: 1
p: 0.3000
>> plot(f,x,y)
4、插值
(1)一维数据插值
>> clear
x=0:10;
y=cos(x);
xi=0:0.25:10;
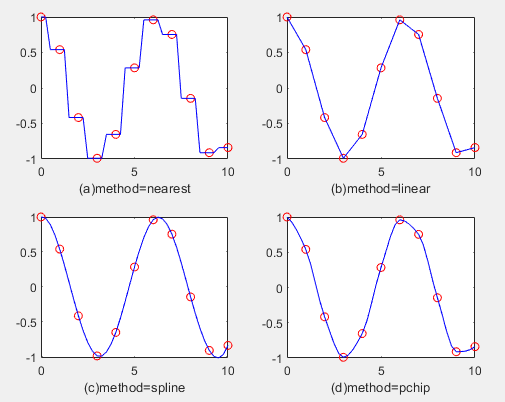
strmod={'nearest','linear','spline','pchip'} % 将插值方法存储到元胞数组
strlb={'(a)method=nearest','(b)method=linear',...
'(c)method=spline','(d)method=pchip'} % 绘图标签
for i=1:4
yi=interp1(x,y,xi,strmod{i}); % 插值
subplot(2,2,i) % 子图
plot(x,y,'ro',xi,yi,'b'),xlabel(strlb(i)) % 绘图
end
strmod =
1×4 cell 数组
{'nearest'} {'linear'} {'spline'} {'pchip'}
strlb =
1×4 cell 数组
1 至 3 列
{'(a)method=nearest'} {'(b)method=linear'} {'(c)method=spline'}
4 列
{'(d)method=pchip'}
(a)临近点插值,找到与其最接近的点插值
(b)线性插值,两个数据点之间连一条直线
(c)样条插值,曲线较平滑
(d)立方插值
(2)二维数据插值
>> clear
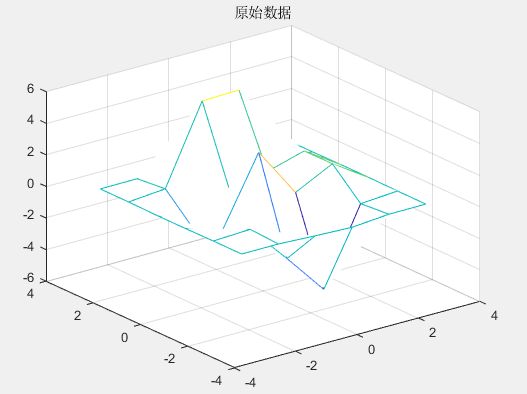
[x,y,z]=peaks(6); % MATLAB自带的测试函数
figure
mesh(x,y,z) % 绘制原始数据图
title('原始数据')
figure
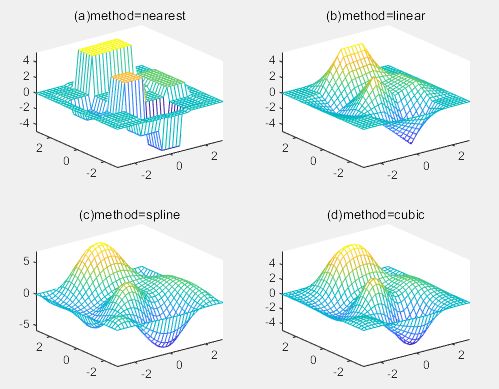
[xi,yi]=meshgrid(-3:0.2:3,-3:0.2:3); % 生成供插值的数据网格
strmod={'nearest','linear','spline','cubic'}; % 将插值方法存储到元胞数组
strlb={'(a)method=nearest','(b)method=linear',...
'(c)method=spline','(d)method=cubic'}; % 绘图标签
figure % 建立新绘图窗口
for i=1:4
zi=interp2(x,y,z,xi,yi,strmod{i}); % 插值
subplot(2,2,i)
mesh(xi,yi,zi); % 绘图
title(strlb{i}) % 图标题
end
(3)三维插值
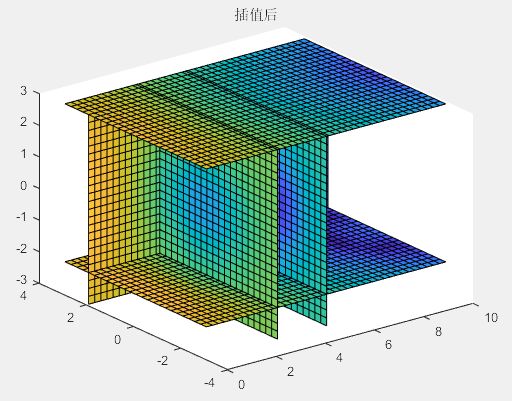
>> figure
[x,y,z,v]=flow(8); % flow是MATLAB自带的测试函数
slice(x,y,z,v,[3,5],2,[-2,3]) % 画切片图
title('插值前')
[xi,yi,zi]=meshgrid(0.1:0.25:10,-3:0.25:3,-3:0.25:3); % 创建插值点数据网格
vi=interp3(x,y,z,v,xi,yi,zi); % 插值
figure
slice(xi,yi,zi,vi,[3,5],2,[-2,3]) % 画插值后切片图
title('插值后')
(4)使用fit函数进行插值
figure
clear
load carbon12alpha
f1 = fit(angle,counts,'nearestinterp'); % 临近点插值
f2 = fit(angle,counts,'pchip'); % 立方插值
p1 = plot(f1,angle,counts);
xlim([min(angle),max(angle)])
hold on
p2 = plot(f2,'b');
hold off
legend([p1;p2],'Counts per Angle','Nearest Neighbor','pchip',...
'Location','northwest')
(5)使用cftool进行插值
APP——>Curve Fitting Tool
第2节 概率统计
1、常用函数
(1)sum函数
>> clear
A = pascal(6)
A =
1 1 1 1 1 1
1 2 3 4 5 6
1 3 6 10 15 21
1 4 10 20 35 56
1 5 15 35 70 126
1 6 21 56 126 252
>> A=A(:,1:4) % 创建演示矩阵
A =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
1 5 15 35
1 6 21 56
>> B=sum(A) % 求各列的和
B =
6 21 56 126
>> C=sum(A') % 求转置后矩阵各列的和
C =
4 10 20 35 56 84
>> D=sum(A,1) % 求第1维方向也就是列方向各元素的和
D =
6 21 56 126
>> E=sum(A,2) % 求第2维方向也就是行方向各元素的和
E =
4
10
20
35
56
84
(2)cumsum函数
>> cumsum(1:5) % 累积求和,按照元素来的
ans =
1 3 6 10 15
>> A=magic(4)
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> cumsum(A) % 列方向上求累积和
ans =
16 2 3 13
21 13 13 21
30 20 19 33
34 34 34 34
>> cumsum(A,1) % 列方向上求累积和
ans =
16 2 3 13
21 13 13 21
30 20 19 33
34 34 34 34
>> cumsum(A,2) % 行方向上求累积和
ans =
16 18 21 34
5 16 26 34
9 16 22 34
4 18 33 34
(3)prod函数
求矩阵元素的积
>> A=magic(4)
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> B=prod(A)
B =
2880 2156 2700 1248
>> B=prod(A,2)
B =
1248
4400
4536
840
(4)cumprod函数
求矩阵或向量的累积乘积
>> A=magic(4)
A =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> B=cumprod(A,2)
B =
16 32 96 1248
5 55 550 4400
9 63 378 4536
4 56 840 840
(5)sort函数
排序函数
>> A = [ 3 7 5;0 4 2 ]
A =
3 7 5
0 4 2
>> sort(A,1) % 列方向排序
ans =
0 4 2
3 7 5
>> sort(A,2) % 行方向排序
ans =
3 5 7
0 2 4
>> sort(A,2,'descend') % 行方向降序排序
ans =
7 5 3
4 2 0
>> [C,IX] = sort(A,2) % 排序并返回下标
C =
3 5 7
0 2 4
IX =
1 3 2
1 3 2
>> B=reshape(18:-1:1,3,3,2) % 创建高维矩阵
B(:,:,1) =
18 15 12
17 14 11
16 13 10
B(:,:,2) =
9 6 3
8 5 2
7 4 1
>> sort(B,1) % 列方向排序
ans(:,:,1) =
16 13 10
17 14 11
18 15 12
ans(:,:,2) =
7 4 1
8 5 2
9 6 3
>> sort(B,2) % 行方向排序
ans(:,:,1) =
12 15 18
11 14 17
10 13 16
ans(:,:,2) =
3 6 9
2 5 8
1 4 7
>> sort(B,3) % 页方向排序
ans(:,:,1) =
9 6 3
8 5 2
7 4 1
ans(:,:,2) =
18 15 12
17 14 11
16 13 10
(6)sortrows函数
>> clear
A = floor(rand(6,7) * 100) % 创建测试矩阵,floor函数用于取整,以便于观察
A =
81 27 95 79 67 70 69
90 54 48 95 75 3 31
12 95 80 65 74 27 95
91 96 14 3 39 4 3
63 15 42 84 65 9 43
9 97 91 93 17 82 38
>> A(1:4,1)=95; A(5:6,1)=76;
A(2:4,2)=7; A(3,3)=73 % 修改部分数据,以体现函数用法
A =
95 27 95 79 67 70 69
95 7 48 95 75 3 31
95 7 73 65 74 27 95
95 7 14 3 39 4 3
76 15 42 84 65 9 43
76 97 91 93 17 82 38
>> B = sortrows(A)
% 按照第1列元素大小对矩阵A进行排序,第一列相等,按照第二列排序
B =
76 15 42 84 65 9 43
76 97 91 93 17 82 38
95 7 14 3 39 4 3
95 7 48 95 75 3 31
95 7 73 65 74 27 95
95 27 95 79 67 70 69
>> B1=sort(A) % 每一列各自分别排序
B1 =
76 7 14 3 17 3 3
76 7 42 65 39 4 31
95 7 48 79 65 9 38
95 15 73 84 67 27 43
95 27 91 93 74 70 69
95 97 95 95 75 82 95
>> C = sortrows(A,2) % 按照第2列的大小进行排序
C =
95 7 48 95 75 3 31
95 7 73 65 74 27 95
95 7 14 3 39 4 3
76 15 42 84 65 9 43
95 27 95 79 67 70 69
76 97 91 93 17 82 38
>> D = sortrows(A,[1 7]) % 按照第1列和第7列进行排序
D =
76 97 91 93 17 82 38
76 15 42 84 65 9 43
95 7 14 3 39 4 3
95 7 48 95 75 3 31
95 27 95 79 67 70 69
95 7 73 65 74 27 95
>> E = sortrows(A,[1 -7]) % 按照第1列和第7列进行排序,第七列按照降序
E =
76 15 42 84 65 9 43
76 97 91 93 17 82 38
95 7 73 65 74 27 95
95 27 95 79 67 70 69
95 7 48 95 75 3 31
95 7 14 3 39 4 3
>> F = sortrows(A, -4) % 按照第4列进行降序排序
F =
95 7 48 95 75 3 31
76 97 91 93 17 82 38
76 15 42 84 65 9 43
95 27 95 79 67 70 69
95 7 73 65 74 27 95
95 7 14 3 39 4 3
>> F = sortrows(A', -4) % 按照行排序
F =
95 95 95 95 76 76
67 75 74 39 65 17
95 48 73 14 42 91
27 7 7 7 15 97
70 3 27 4 9 82
79 95 65 3 84 93
69 31 95 3 43 38
2、概率函数
(1)std函数
标准差函数
s=std(x,flag):若flag=0,则等同于s=std(x);若flag=1,则按照公式(2)求x的标准差,默认为1
>> A=magic(5)
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> s1=std(A,0,1) % flag=0,1代表第一维,即列,对每一列求标准差
s1 =
7.2457 8.0623 9.4868 8.0623 7.2457
>> s2=std(A,1,1)
s2 =
6.4807 7.2111 8.4853 7.2111 6.4807
>> s3=std(A,0,2)
s3 =
8.8034
7.2457
8.0623
7.2457
8.8034
(2)var函数
方差函数,与std用法一样
>> A=magic(5)
A =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> v1=var(A) % 样本方差
v1 =
52.5000 65.0000 90.0000 65.0000 52.5000
>> v2=var(A,0,1) % 和v1结果相同
v2 =
52.5000 65.0000 90.0000 65.0000 52.5000
>> v3=var(A,1,1) % 计算方差
v3 =
42 52 72 52 42
(3)cov函数
cov函数用于求协方差矩阵,计算协方差的数学公式为:cov(x1,x2)=E[(x1-u1)(x2-u2)]
>> A = [-1 1 2 ; -2 3 1 ; 4 0 3]
A =
-1 1 2
-2 3 1
4 0 3
>> C=cov(A) % 协方差矩阵
C =
10.3333 -4.1667 3.0000
-4.1667 2.3333 -1.5000
3.0000 -1.5000 1.0000
>> v = diag(cov(A))' % 矩阵A每列的方差
v =
10.3333 2.3333 1.0000
>> V = var(A) % 矩阵A每列的方差
V =
10.3333 2.3333 1.0000
(4)corrcoef函数
相关系数
>> rng('default')
>> x = randn(30,4);% 30*4的二维数组
y = randn(30,4);
y(:,4) = sum(x,2); % introduce correlation
>> [r1,p1] = corrcoef(x,y) % 将所有元素转换为列向量,然后计算
r1 = % 相关系数
1.0000 0.1252
0.1252 1.0000
p1 =
1.0000 0.1729
0.1729 1.0000
>> [r2,p2] = corrcoef(x(:),y(:)) % 将所有元素转换为列向量,然后计算
r2 =
1.0000 0.1252
0.1252 1.0000
p2 =
1.0000 0.1729
0.1729 1.0000
>> [r3,p3] = corrcoef(x(:,1),y(:,1)) % 对x的第一列与y的第一列计算相关系数
r3 =
1.0000 -0.1686
-0.1686 1.0000
p3 =
1.0000 0.3731
0.3731 1.0000
>> [r,p] = corr(x,y) % 计算相关系数的矩阵
r =
-0.1686 -0.0363 0.2278 0.6901
0.3022 0.0332 -0.0866 0.2617
-0.3632 -0.0987 -0.0200 0.3504
-0.1365 -0.1804 0.0853 0.4908
p =
0.3731 0.8489 0.2260 0.0000
0.1045 0.8619 0.6491 0.1624
0.0485 0.6039 0.9166 0.0577
0.4721 0.3400 0.6539 0.0059
>> [i,j] = find(p<0.05) % 查找显著性相关
i =
3
1
4
j =
1
4
4
3、分布函数、逆分布函数和随机数
(1)泊松分布与正态分布的关系
>> Lambda=20;
x=0:50;
yd_p=poisspdf(x,Lambda); % 泊松分布
yd_n=normpdf(x,Lambda,sqrt(Lambda)); % 正态分布
plot(x,yd_n,'b-',x,yd_p,'r+') % 绘图
>> text(30,0.07,'\fontsize{12} {\mu} = {\lambda} = 20') % 在图中作标注
legend('正态分布','泊松分布')
(2)![]() 分布逆累积分布函数应用
分布逆累积分布函数应用
>> v=4;xi=0.9;
x_xi=chi2inv(xi,v); % 设置信水平为90%
x=0:0.1:15;
yd_c=chi2pdf(x,v); % 计算自由度(4)的概率密度函数
% 绘制图形,并给置信区间填色
plot(x,yd_c,'b'),hold on
xxf=0:0.1:x_xi;
yyf=chi2pdf(xxf,v); % 为填色而计算
fill([xxf,x_xi],[yyf,0],'g') % 加入点(x_xi,0)使填色区域封闭
% 添加注释
text(x_xi*1.01,0.01,num2str(x_xi))
text(10,0.16,['\fontsize{16} x~{\chi}^2' '(4)'])
text(1.5,0.08,'\fontname{隶书}\fontsize{22}置信水平0.9')
hold off
(2)生成既定直方图分布的随机数
function rm=RDrnd(countData,m)
% 生成与既有直方图分布相同的随机数
% countData 既有直方图分布
% m 生成m个随机数
% 生成的随机数为归一化之后的
Nbins=length(countData); % 直方图有多少柱子
C=sum(countData); % 直方图总计数
edg=cumsum(countData);
Edg=zeros(length(countData),2);
Edg(2:end,1)=edg(1:end-1);
Edg(:,2)=edg(1:end);
% Edg=[0 edg(1:end-1);edg(1:end)]';
r=rand(m,1)*C;
a=linspace(0,1,Nbins+1);
b=[a(1:end-1);a(2:end)]';
rm=zeros(m,1);
for i=1:m
idx1=r(i)>=Edg(:,1);
idx2=r(i)>> countData=randperm(8)
countData =
1 6 7 4 5 3 2 8
>> bar(countData)
>> rm=RDrnd(countData,10000); % 生成1w个随机数
figure
histogram(rm,8) % 用直方图进行统计
4、描述统计学
描述统计(descriptive statistics),又称叙述统计,是统计学中,来描绘或总结观察量的基本情况的统计总称。其与推论统计相对应。
研究者可以透过对数据资料的图像化处理,将资料摘要变为图表,以直观了解整体资料分布的情况。通常会使用的工具是频数分布表与图示法,如多边图、直方图、饼图、散点图等。
研究者也可以透过分析数据资料,以了解各变量内的观察值集中与分散的情况。运用的工具有:集中量数,如平均数、中位数、众数、几何平均数、调和平均数。与变异量数,如全距、平均差、标准差、相对差、四分差。
数据的次数分配情况,往往会呈现正态分布。为了表示测量数据与正态分布偏离的情况,会使用偏度、峰度这两种统计数据。
为了解个别观察值在整体中所占的位置,会需要将观察值转换为相对量数,如百分等级、标准分数、四分位数等。
(1)几何平均数
>> x = exprnd(1,10,6)
x =
0.2254 0.1834 0.4222 0.1451 1.0470 0.5497
0.1982 2.7704 0.4563 1.0825 0.3570 0.0393
0.9980 0.5108 0.9118 2.7604 0.7160 2.7586
0.2108 2.8122 1.0277 1.3210 0.1980 0.3293
2.8021 1.4544 0.7897 2.3798 1.1088 0.1031
2.3996 1.5155 0.1756 0.3985 2.3637 1.6338
0.2162 1.3500 0.9416 0.0567 0.1842 0.1080
0.6033 0.5120 0.1169 0.4211 0.8517 0.1965
0.1108 0.3640 0.2089 0.8762 1.3589 0.4065
1.6774 0.0811 0.1957 1.4204 0.5011 0.4206
>> geometric = geomean(x)
geometric =
0.5230 0.7105 0.4029 0.6619 0.6563 0.3220
(2)调和平均数
>> harmonic = harmmean(x)
harmonic =
0.3134 0.3670 0.3021 0.2965 0.4793 0.1662
(3)峰态
>> X = randn([5 4])
X =
0.1923 0.4845 -0.2388 -0.3610
-1.5175 0.7883 0.9647 -0.2477
0.5714 -1.6560 -0.9639 -0.8803
-0.5108 1.6262 0.0542 0.2874
-0.3383 0.6934 0.8776 -0.2923
>> k = kurtosis(X)
k =
2.1565 2.7771 1.6814 2.4532
(4)中心矩
>> m = moment(X,3)
m =
-0.1754 -1.3070 -0.0857 0.0009
(5)偏态
>> y = skewness(X)
y =
-0.4880 -1.0008 -0.2293 0.0182
(6)范围
>> rv = normrnd(0,1,1000,5);
near6 = range(rv) % 最大的数-最小的数
near6 =
6.6636 7.0172 6.5374 7.5891 6.4757
(7)四分位差
>> x=1:100;
iqr(x)
ans =
50
>> x=1:500;
iqr(x)
ans =
250
>> pd = makedist('Normal',0,1);% 生成正态分布函数
r = iqr(pd)
r =
1.3490
(8)百分位
>> x=1:100;
Y = prctile(x,42)
Y =
42.5000
>> X = (1:10)'*(1:5)
X =
1 2 3 4 5
2 4 6 8 10
3 6 9 12 15
4 8 12 16 20
5 10 15 20 25
6 12 18 24 30
7 14 21 28 35
8 16 24 32 40
9 18 27 36 45
10 20 30 40 50
>> Y1 = prctile(X,[25 50 75],1) % 对每一列求25%,50%,75%的百分位
Y1 =
3.0000 6.0000 9.0000 12.0000 15.0000
5.5000 11.0000 16.5000 22.0000 27.5000
8.0000 16.0000 24.0000 32.0000 40.0000
>> Y2 = prctile(X,[25 50 75],2) % 对每一行求25%,50%,75%的百分位
Y2 =
1.7500 3.0000 4.2500
3.5000 6.0000 8.5000
5.2500 9.0000 12.7500
7.0000 12.0000 17.0000
8.7500 15.0000 21.2500
10.5000 18.0000 25.5000
12.2500 21.0000 29.7500
14.0000 24.0000 34.0000
15.7500 27.0000 38.2500
17.5000 30.0000 42.5000
(9)分位数
>> rng('default'); % for reproducibility
x = normrnd(0,1,1,10)
x =
1 至 7 列
0.5377 1.8339 -2.2588 0.8622 0.3188 -1.3077 -0.4336
8 至 10 列
0.3426 3.5784 2.7694
>> y1 = quantile(x,0.30)
y1 =
-0.0574
>> y2 = quantile(x,[0.25, 0.5, 0.75])
y2 =
-0.4336 0.4401 1.8339
>> y3 = quantile(x,3)
y3 =
-0.4336 0.4401 1.8339
(10)频率表
>> tabulate([1 2 4 4 3 4])
Value Count Percent
1 1 16.67%
2 1 16.67%
3 1 16.67%
4 3 50.00%
第3节 统计可视化
1、分布曲线
分布曲线可以展示数据的分布情况,可以让人从视觉上对数据是否符合一个特定分布、是否有异常值等进行判断。MATLAB提供了以下几种分布曲线绘制方式:
- 正态概率曲线可以用来评估一组样本是否是一个正态分布。相应函数为normplot。
- 分位数图可以用来评估两组样本是否属于同一类分布,并且相对于位置和刻度都很稳定。相应函数为qqplot。
- 累计分布曲线可以用来显示样本数据的累积分布情况,可以用来估计其是否和特定分布的理论累计分布曲线一致。相应的函数有cdfplot,ecdf和stairs。
- 其他概率分布曲线。相应的函数为probplot。
(1)正态概率曲线
正态概率曲线可以用来评估一组样本是否是一个正态分布。相应函数为normplot。
>> rng default; % For reproducibility
x = normrnd(10,1,25,1); % mu = 10 sigma = 1,25行1列的一组数
normplot(x)
有几点说明:
- 纵轴对应的是正态分布的概率
- 红色线的虚线、实线对应25和75百分位
- 纵轴的刻度并不线性,和相应分位数之间的距离对应
- 样本点越接近红色直线,则越符合正态分布
>> x = exprnd(10,100,1); % mu=10 指数分布
normplot(x)
从此图可以看出,并不符合正态分布
(2)分位数图
分位数图可以用来评估两组样本是否属于同一类分布,并且相对于位置和刻度都很稳定。相应函数为qqplot。
>> x = poissrnd(10,50,1); % lambda=10
y = poissrnd(5,100,1); % lambda=5
qqplot(x,y)
从图中可以看出,x和y是同一类分布,泊松分布
>> x = normrnd(5,1,100,1);
y = wblrnd(2,0.5,100,1);
qqplot(x,y)
上图是这样画出来的:先对所有x排序,再对所有y排序,在图上标出最小的x对应的最小的y,在第一、三两个四分位之间画直线,看其他点是否落在其延长线上。
>> figure;scatter(sort(x),sort(y))
ylim([-10 35])
(3)累积分布曲线
累计分布曲线可以用来显示样本数据的累积分布情况,可以用来估计其是否和特定分布的理论累计分布曲线一致。相应的函数有cdfplot,ecdf和stairs。
>> y = evrnd(0,3,100,1); % 极值分布
cdfplot(y)
>> hold on
x = -20:0.1:10;
f = evcdf(x,0,3);% 极值分布的理论曲线
plot(x,f,'m')
legend('Empirical','Theoretical','Location','NW')
(4)概率分布曲线
和正态概率分布曲线规则一致,只是采用的分布并不是正态分布。在第一和第三两个四分位之间画一条直线,看其他数据点是否落在这个直线上。
>> x1 = wblrnd(3,3,100,1); % Weibull distribution
x2 = raylrnd(3,100,1); % Rayleigh distribution
probplot('weibull',[x1 x2])
legend('Weibull Sample','Rayleigh Sample','Location','NW')
y轴刻度等于相应两个分位数之间的距离。
2、统计可视化
(1)Andrews plot
假设X数组每行代表一个样本,每列代表一个变量,每行用如下公式计算
>> clear
load fisheriris
>> andrewsplot(meas,'group',species)
>> figure
andrewsplot(meas,'group',species,'quantile',.25)
![]()
(2)平行坐标图
>> figure
load fisheriris
labels = {'Sepal Length','Sepal Width','Petal Length','Petal Width'};
parallelcoords(meas,'Group',species,'Labels',labels)
figure
parallelcoords(meas,'group',species,'labels',labels,...
'quantile',.25) % 分组,标签,分位数
(3)箱形图
(3)箱形图
于1977年由美国著名统计学家约翰·图基(John Tukey)发明。
它能显示出一组数据的最大值、最小值、中位数、及上下四分位数。
>> load carsmall % 关于汽车的一组测试数据
>> boxplot(MPG) % MPG是油耗
>> xlabel('All Vehicles')
ylabel('Miles per Gallon (MPG)')
title('Miles per Gallon for All Vehicles')
>> boxplot(MPG,Origin) % 画出每个国家的
title('Miles per Gallon by Vehicle Origin')
xlabel('Country of Origin')
ylabel('Miles per Gallon (MPG)')
(4)Glyph plot
>> load carsmall
X = [Acceleration Displacement Horsepower MPG Weight];% 五根线的长短代表了五个量的大小
glyphplot(X,'standardize','column','obslabels',Model,'grid',[2 2],...
'page','scroll'); % 标准形式,滑动条形式
>> glyphplot(X,'glyph','face','obslabels',Model,'grid',[2 3],'page',9); % 有的变量对应鼻子,眼睛等,最多支持17个变量
(5)gscatter
散点图
Scatter plot by group 分组同时绘制
>> load carsmall
gscatter(Weight,MPG,Model_Year,'','xos')
>> xvars = [Weight Displacement Horsepower];
yvars = [MPG Acceleration];
gplotmatrix(xvars,yvars,Model_Year,'','xos') % 2行3列
(6)双变量直方图
>> load carbig
>> X = [MPG,Weight];
hist3(X,[7 7]);
xlabel('MPG'); ylabel('Weight');
% 半透明设置
hist3(X,[7 7],'FaceAlpha',.65); % FaceAlpha,显示透明
xlabel('MPG'); ylabel('Weight');
set(gcf,'renderer','opengl');
set(get(gca,'child'),'FaceColor','interp','CDataMode','auto');
(7)参考曲线
refcurve
>> p = [1 -2 -1 0];
t = 0:0.1:3;
rng default % For reproducibility
y = polyval(p,t) + 0.5*randn(size(t));
plot(t,y,'ro')
>> h = refcurve(p)
h =
Line - 属性:
Color: [0 0.4470 0.7410]
LineStyle: '-'
LineWidth: 0.5000
Marker: 'none'
MarkerSize: 6
MarkerFaceColor: 'none'
XData: [1×100 double]
YData: [1×100 double]
ZData: [1×0 double]
显示 所有属性
>> h.Color = 'r';
q = polyfit(t,y,3);
refcurve(q)
legend('Data','Population Mean','Fitted Mean',...
'Location','NW')
![]()
此时蓝色线是自己计算生成的
(8)参考线
>> x = 1:10;
y = x + randn(1,10);
scatter(x,y,25,'b','*') % 绘出散点图
>> mu = mean(y);
hline = refline([0 mu]); % 画一条平均数的直线
hline.Color = 'r';
(9)scatterhist 散点图+直方图
>> load fisheriris.mat;
x = meas(:,1);
y = meas(:,2);
>> scatterhist(x,y) % 散点图+直方图
>> figure
scatterhist(x,y,'Group',species,'Kernel','on') % 分组,Kernel,将直方图变成曲线形式
![]()
>> figure
scatterhist(x,y,'Group',species,'Kernel','on','Location','SouthEast',...
'Direction','out','Color','kbr','LineStyle',{'-','-.',':'},...
'LineWidth',[2,2,2],'Marker','+od','MarkerSize',[4,5,6]); % 指定详细绘图信息
%更改直方图的位置,在东面和南面,方向变成out,颜色,线型,线宽,数据点大小
>> figure
h = scatterhist(x,y,'Group',species);
>> hold on;
clr = get(h(1),'colororder'); 提取出散点图的颜色
boxplot(h(2),x,species,'orientation','horizontal',...
'label',{'','',''},'color',clr); % 将下面的图变成箱型图
>> boxplot(h(3),y,species,'orientation','horizontal',...
'label', {'','',''},'color',clr);% 将左边的图变成箱型图
>> set(h(2:3),'XTickLabel','');
view(h(3),[270,90]); % Rotate the Y plot
axis(h(1),'auto'); % Sync axes
hold off;
第4节 文件I/O
1、数据导入工具
(1)导入grades.txt
可以按住ctrl,选择某几列或者某几行,点击导入
可以更改字段类型
双击,可以更改列名与文件名
>> grades
grades =
4×4 table
John Ann Mark Rob
____ ____ ____ ____
88.4 91.5 89.2 77.3
83.2 88 67.8 91
77.8 76.3 NaN 92.5
92.1 96.4 81.2 84.6
>> grades.John
ans =
88.4000
83.2000
77.8000
92.1000
(2)导入T3.txt文件
>> B.T
ans =
3×1 datetime 数组
01 01 2014
01 02 2014
01 03 2014
>> B.T.Format
ans =
'dd MM yyyy'
>> B.T.Format = 'yyyy-MM-dd'
B =
3×3 table
T x y
__________ ____ _____
2014-01-01 20.2 100.5
2014-02-01 21.6 102.7
2014-03-01 20.7 99.8
(3)导入tempdata.xls
根据sheet页,导入
2、MAT文件的读写
(1)目录的操作
>> file = 'F:\研二上\数模\课件\MATLAB课件\第4章 Matlab数据分析及各种算法介绍\第4节 文件IO\【课件】文件IO\L11 文件IO\L11.mlx'
file =
'F:\研二上\数模\课件\MATLAB课件\第4章 Matlab数据分析及各种算法介绍\第4节 文件IO\【课件】文件IO\L11 文件IO\L11.mlx'
>> [pathstr,name,ext]=fileparts(file) % 分解文件名
pathstr =
'F:\研二上\数模\课件\MATLAB课件\第4章 Matlab数据分析及各种算法介绍\第4节 文件IO\【课件】文件IO\L11 文件IO'
name =
'L11'
ext =
'.mlx'
>> f = fullfile(pathstr,[name,ext]) % 路径和文件名组合起来,可以自动补全分隔符
f =
'F:\研二上\数模\课件\MATLAB课件\第4章 Matlab数据分析及各种算法介绍\第4节 文件IO\【课件】文件IO\L11 文件IO\L11.mlx'
>> fullfile(matlabroot, 'toolbox', 'matlab', 'general', 'Contents.m') % 代表安装matlab的根目录
ans =
'E:\wenjiananzhaung\MATLAB\toolbox\matlab\general\Contents.m'
(2)save函数
save函数的调用语法如下:
save filename
若没有指定输出路径,那么调用save函数以及后文所涉及的数据保存函数所输出的文件均保存在MATLAB当前目录下。
另外也可以只保存Workspace中的指定变量:
save filename var1 var2 ... varN
在变量名中使用通配符(*),可以保存名字类似的变量。例如使用下面的命令,就可以保存名字以str开始的变量:
save strinfo str
>> S.a = 12.7; S.b = {'abc', [4 5; 6 7]}; S.c = 'Hello!';
>> save newstruct.mat S; % 保存newstruct.mat 中的S变量,newstruct.mat可以自动生成
>> save('newstruct1.mat','S');
>> clear
>> load('newstruct1.mat')
>> clear
>> load newstruct.mat
3、TXT文件的读写
对于简单的txt来说
>> clear
>> load testdata1.txt
>> clear
>> load test\testdata1.txt
>> A=dlmread('testdata2.dat',';')
A =
7.2000 8.5000 6.2000 6.6000
5.4000 9.2000 8.1000 7.2000
>> A=csvread('testdata3.dat')
A =
7.2000 8.5000 6.2000 6.6000
5.4000 9.2000 8.1000 7.2000
4、有标题行的情况
>> clear
>> fid = fopen('grades.txt', 'r'); % fid为返回的文件句柄,r代表只读形式
>> grades = textscan(fid, '%f %f %f %f', 3, 'headerlines', 1);
% %f代表数据类型
% 3 代表执行3次,这样就可以读取前三行,
% headerlines代表有几个标题行
>> fclose(fid);
>> grades{:}
ans =
88.4000
83.2000
77.8000
ans =
91.5000
88.0000
76.3000
ans =
89.2000
67.8000
92.5000
ans =
77.3000
91.0000
NaN
>> fid = fopen('grades.txt', 'r');
>> grades = textscan(fid, '%f %f %f %f', 3, 'headerlines', 1);
>> grades = textscan(fid, '%f %f %f %f', 3, 'headerlines', 1);
% textscan是每次读取一行,再次读的时候是从下一行开始读
% 如果使用fclose关闭,下次再打开的时候就从第一行开始读了
>> grades{:}
ans =
92.1000
ans =
96.4000
ans =
81.2000
ans =
84.6000
5、复杂格式情况
09/12/2005 Level1 12.34 45 1.23e10 inf Nan Yes 5.1+3i
10/12/2005 Level2 23.54 60 9e19 -inf 0.001 No 2.2-.5i
11/12/2005 Level3 34.90 12 2e5 10 100 No 3.1+.1i
>> filename = fullfile(matlabroot,'examples','matlab','scan1.dat'); % matlab自带的文件
>> filename
filename =
'D:\MATLAB\R2018a\examples\matlab\scan1.dat'
>> fileID = fopen(filename);
>> C = textscan(fileID,'%s %s %f32 %d8 %u %f %f %s %f');
% %s代表文本,%f小数,%d整数
>> fclose(fileID);
>> celldisp(C) % 元胞数组
C{1}{1} =
09/12/2005
C{1}{2} =
10/12/2005
C{1}{3} =
11/12/2005
C{2}{1} =
Level1
C{2}{2} =
Level2
C{2}{3} =
Level3
C{3} =
12.3400
23.5400
34.9000
C{4} =
45
60
12
C{5} =
4294967295
4294967295
200000
C{6} =
Inf
-Inf
10
C{7} =
NaN
0.0010
100.0000
C{8}{1} =
Yes
C{8}{2} =
No
C{8}{3} =
No
C{9} =
5.1000 + 3.0000i
2.2000 - 0.5000i
3.1000 + 0.1000i
>> fileID = fopen(filename);
>> C1 = textscan(fileID,'%{dd/mm/yyyy}D %s %f32 %d8 %u %f %f %s %f');
% D代表日期
>> fclose(fileID);
% 文件打开之后要及时关闭
>> C1{1}
ans =
3×1 datetime 数组
09/12/2005
10/12/2005
11/12/2005
6、txt文件的写入
>> A = [ 1 2 3 4 ; 5 6 7 8 ]
A =
1 2 3 4
5 6 7 8
>> save my_dataout.txt A -ASCII % 使用save写入
>> dlmwrite('my_dataout1.txt',A, ';') % 使用dlmwrite写入
7、Excel文件读写
>> d = {'Time', 'Temp'; 12 98; 13 99; 14 97}
d =
4×2 cell 数组
{'Time'} {'Temp'}
{[ 12]} {[ 98]}
{[ 13]} {[ 99]}
{[ 14]} {[ 97]}
>> xlswrite('tempdata.xls', d, 'Temperatures', 'E1');
% 'Temperatures'代表所存的sheet页,E1代表从哪个位置开始存
Excel文件的读取
>> ndata = xlsread('tempdata.xls', 'Temperatures')
ndata =
12 98
13 99
14 97
>> [ndata1, headertext1] = xlsread('tempdata.xls', 'Temperatures') %既读出数值数据,又读出文本数据(标题行也读出来了)
ndata1 =
12 98
13 99
14 97
headertext1 =
1×2 cell 数组
{'Time'} {'Temp'}
8、读取为表格readtable
>> filename = fullfile(matlabroot,'examples','matlab','myCsvTable.dat');
>> filename
filename =
'D:\MATLAB\R2018a\examples\matlab\myCsvTable.dat'
>> T = readtable(filename)
T =
5×6 table
LastName Gender Age Height Weight Smoker
__________ ______ ___ ______ ______ ______
'Smith' 'M' 38 71 176 1
'Johnson' 'M' 43 69 163 0
'Williams' 'F' 38 64 131 0
'Jones' 'F' 40 67 133 0
'Brown' 'F' 49 64 119 0
>> T1 = readtable(filename,'Format','%s%s%u%f%f%s')
T1 =
5×6 table
LastName Gender Age Height Weight Smoker
__________ ______ ___ ______ ______ ______
'Smith' 'M' 38 71 176 '1'
'Johnson' 'M' 43 69 163 '0'
'Williams' 'F' 38 64 131 '0'
'Jones' 'F' 40 67 133 '0'
'Brown' 'F' 49 64 119 '0'
>> filename = fullfile(matlabroot,'examples','matlab','german_dates.txt');
>> filename
filename =
'D:\MATLAB\R2018a\examples\matlab\german_dates.txt'
% 是一个德语文件,有些乱码
>> T3 = readtable(filename,'ReadVariableNames',false,... % 不读取变量名
'Format','%{dd MMMM yyyy}D %f %f',... % 显示为日期格式
'FileEncoding','ISO-8859-15',... % 指定德语的编码
'DateLocale','de_DE')
T3 =
3×3 table
Var1 Var2 Var3
__________ ____ _____
01 一月 2014 20.2 100.5
01 二月 2014 21.6 102.7
01 三月 2014 20.7 99.8
>> writetable(T3)
>> type 'T3.txt' % 查看该文件
Var1,Var2,Var3
01 一月 2014,20.2,100.5
01 二月 2014,21.6,102.7
01 三月 2014,20.7,99.8
第5节 优化工具箱
- 最小值优化
这一组求解器用于求解目标函数在初始点x0附近的最小值位置。适用于无约束优化、线性规划、二次规划和一般的非线性规划。
- 多目标最小值优化
这一组求解器用于求解一组方程极大值中的极小值(fminimax),还可以求解一组方程低于某一特定值的定义域(fgoalattain)。
- 方程求解器
这一组求解器用于求解一个标量或者向量非线性方程f(x) = 0在初始点x0附近的解。也可以将方程求解当作是一种形式的优化,因为它等同于在x0附近找到一个f(x)模的最小值。
- 最小二乘(曲线拟合)求解器
这一组求解器用于求解一组平方和的最小值。这样的问题常在求一组数据的拟合模型的过程中出现。这组求解器适用于求问题非负解、边界限定或者线性约束解问题,还适用于根据数据拟合出参数化非线性模型。
为此,我们应根据自己的实际需要,根据实际的约束条件来选择相应的求解器。4种求解器所对应的所有优化函数如所示。
1、极小值优化
(1)标量最小值优化
求解单变量最优化问题的方法有多种,根据目标函数是否需要求导,可以分为两类,即直接法和间接法。直接法不需要对目标函数进行求导,而间接法则需要用到目标函数的导数。
常用的一维直接法主要有消去法和近似法两种。
- 消去法:该法利用单峰函数具有的消去性质进行反复迭代,逐渐消去不包含极小点的区间,缩小搜索区间,直到搜索区间缩小到给定的允许精度为止。一种典型的消去法为黄金分割法(Golden Section Search)。黄金分割法的基本思想是在单峰区间内适当地插入两点,将区间分为3段,然后通过比较这两点函数值的大小来确定是删去最左段还是最右段,或同时删去左右两段,而保留中间段。重复该过程可以使区间无限缩小。插入点的位置放在区间的黄金分割点及其对称点上,所以该法称为黄金分割法。该法的优点是算法简单,效率较高,稳定性好。
- 多项式近似法:该法用于目标函数比较复杂的情况。此时搜索一个与它近似的函数代替目标函数,并用近似函数的极小点作为原函数极小点的近似。常用的近似函数为二次和三次多项式。二次插值法的计算速度比黄金分割法快,但是对于一些强烈扭曲或可能多峰的函数,该法的收敛速度会变得很慢,甚至失败。
间接法需要计算目标函数的导数,优点是计算速度很快。常见的间接法包括牛顿切线法、对分法、割线法和三次插值多项式近似法等。优化工具箱中用得较多的是三次插值法。如果函数的导数容易求得,一般来说应首先考虑使用三次插值法,因为它具有较高的效率。在只需要计算函数值的方法中,二次插值法是一个很好的方法,它的收敛速度较快,特别是在极小点所在区间较小时尤为如此。黄金分割法则是一种十分稳定的方法,并且计算简单。基于以上分析,MATLAB优化工具箱中使用得较多的方法是二次插值法、三次插值法、二次三次混合插值法和黄金分割法。
MATLAB优化工具箱提供了fminbnd函数来进行标量最小值问题的优化求解。
例:对边长为3m的正方形铁板,在4个角处剪去相等的正方形,以制成方形无盖水槽,问如何剪才能使水槽的容积最大?
function f = myfun1(x)
f = -(3-2*x).^2 * x;
>> x = fminbnd(@myfun1,0,1.5) %
% x = fminbnd(fun,x1,x2):返回标量函数fun在条件x1 < x < x2下取最小值时自变量x的值
x =
0.5000
>> y= -myfun1(x) % 调用myfun1函数来计算水槽的最大容积
y =
2.0000
(2)无约束最小值优化
无约束最优化问题在实际应用中也比较常见,如工程中常见的参数反演问题。另外,许多有约束最优化问题也可以转化为无约束最优化问题进行求解。
求解无约束最优化问题的方法主要有两类,即直接搜索法(Search method)和梯度法(Gradient method)。
直接搜索法适用于目标函数高度非线性,没有导数或导数很难计算的情况。实际工程中很多问题都是非线性的,因此直接搜索法不失为一种有效的解决办法。常用的直接搜索法为单纯形法,此外还有Hooke-Jeeves搜索法、Pavell共轭方向法等,其缺点是收敛速度慢。
在函数的导数可求的情况下,梯度法是一种更优的方法,该法利用函数的梯度(一阶导数)和Hessian矩阵(二阶导数)构造算法,可以获得更快的收敛速度。函数f(x)的负梯度方向即反映了函数的最大下降方向。当搜索方向取为负梯度方向时,称为最速下降法。但当需要最小化的函数有一狭长的谷形值域时,该法的效率则很低。常见的梯度法有最速下降法、Newton法、Marquart法、共轭梯度法和拟牛顿法(Quasi-Newton method)等。在这些方法中,用得最多的是拟牛顿法。
在MATLAB中,有fminunc和fminsearch两个函数用来求解无约束最优化问题。
当函数不连续,或者无法求导时,使用fminsearch函数,可以应用的范围更广,但是计算速度会慢一些。
例:求函数![]() 的最小值
的最小值
function f = myfun2(x)
f = 3*x(1)^2 + 2*x(1)*x(2) + x(2)^2; % 目标函数
>> x0 = [1,1]; % 初始点,一般不影响结果,如果有n个变量,x0中就有n个元素
[x,fval] = fminunc(@myfun2,x0) % 因为并没有定义函数句柄,所以要加上@符号
Local minimum found.
Optimization completed because the size of the gradient is less than
the default value of the optimality tolerance.
x =
1.0e-06 *
0.2541 -0.2029
fval =
1.3173e-13
求banana方程的最小值:
![]()
在指定a的情况下求这个方程的最小值
>> a=3;
>> banana = @(x)100*(x(2)-x(1)^2)^2+(a-x(1))^2;
>> options = optimset('Display','iter','PlotFcns',@optimplotfval);
>> [x,fval,exitflag,output] = fminsearch(banana, [-1.2, 1], ...
optimset('TolX',1e-8,'Display','iter','PlotFcns',@optimplotfval))
% optimset设置参数
% optimset('TolX',1e-8)用来设置算法终止误差
% 'Display','iter' 显示出迭代过程
% 'PlotFcns',@optimplotfval 设置绘图函数
优化已终止:
当前的 x 满足使用 1.000000e-08 的 OPTIONS.TolX 的终止条件,
F(X) 满足使用 1.000000e-04 的 OPTIONS.TolFun 的收敛条件
x =
3.0000 9.0000
fval =
2.4045e-18
exitflag =
1
output =
包含以下字段的 struct:
iterations: 159 % 迭代次数
funcCount: 303 % 函数被调用次数
algorithm: 'Nelder-Mead simplex direct search'
message: '优化已终止:↵ 当前的 x 满足使用 1.000000e-08 的 OPTIONS.TolX 的终止条件,↵F(X) 满足使用 1.000000e-04 的 OPTIONS.TolFun 的收敛条件↵'
(3)线性规划
线性规划是处理线性目标函数和线性约束的一种较为成熟的方法,目前已经广泛地应用于军事、经济、工业、农业、教育、商业和社会科学等许多方面。
线性规划的标准形式要求目标函数最小化,约束条件取等式,变量非负。不符合这几个条件的线性模型要首先转换成标准形。线性规划的求解方法主要是单纯形法。
MATLAB优化工具箱提供了linprog函数用来进行线性规划的求解
linprog函数适用的线性规划问题标准形式为:
例:求如下函数的最小值
![]()
>> f = [-5; -4; -6]; % 用矩阵表示目标函数
>> A = [1 -1 1
3 2 4
3 2 0]; % 用矩阵形式表示约束条件系数
>> b = [20; 42; 30]; % 约束条件
>> lb = zeros(3,1); % 下界约束
>> [x,fval,exitflag,output,lambda] = linprog(f,A,b,[],[],lb)
% [],[]代表的是Aeq,Beq,等式约束,需要用空格占位
Optimal solution found.
x =
0
15.0000
3.0000
fval =
-78
exitflag =
1
output =
包含以下字段的 struct:
iterations: 3
constrviolation: 0
message: 'Optimal solution found.'
algorithm: 'dual-simplex'
firstorderopt: 1.7764e-15
lambda = % 求解过程中的主动约束
包含以下字段的 struct:
lower: [3×1 double]
upper: [3×1 double]
eqlin: []
ineqlin: [3×1 double]
>> lambda.ineqlin % 不等式约束,第一个没起到作用
ans =
0
1.5000
0.5000
>> lambda.lower % 下界约束,第二第三个没起到作用
ans =
1.0000
0
0
Lambda域中向量里的非零元素可以反映出求解过程中的主动约束。在本例的结果中可以看出,第2个和第3个不等式约束(lambda.ineqlin)和第1个下界约束(lambda.lower)是主动约束。
(4)二次规划
二次规划是非线性规划中一类特殊的数学规划问题,它的解是可以通过求解得到的。通常通过解其库恩-塔克条件(K-T条件),获取一个K-T条件的解,称为K-T对,其中与原问题的变量对应的部分称为K-T点。二次规划的一般形式为:
其中![]() 为对称矩阵。二次规划分为凸二次规划与非凸二次规划两者,前者的K-T点便是其全局极小值点,而后者的K-T点则可能连局部极小值点都不是。若它的目标函数是二次函数,则约束条件是线性的。求解二次规划的方法很多,较简便易行的是沃尔夫法,它是依据K-T条件,在线性规划单纯形法的基础上加以修正而得到的。此外还有莱姆基法、毕尔法、凯勒法等。MATLAB优化工具箱中提供了quadprog函数用来进行二次规划的求解。
为对称矩阵。二次规划分为凸二次规划与非凸二次规划两者,前者的K-T点便是其全局极小值点,而后者的K-T点则可能连局部极小值点都不是。若它的目标函数是二次函数,则约束条件是线性的。求解二次规划的方法很多,较简便易行的是沃尔夫法,它是依据K-T条件,在线性规划单纯形法的基础上加以修正而得到的。此外还有莱姆基法、毕尔法、凯勒法等。MATLAB优化工具箱中提供了quadprog函数用来进行二次规划的求解。
例:求下面函数的最小值
![]()
首先要将方程写成矩阵形式
>> H = [1 -1; -1 2];
>> f = [-2; -6];
>> A = [1 1; -1 2; 2 1]; % 线性不等式约束
>> b = [2; 2; 3]; % 线性不等式约束
>> lb = zeros(2,1);
>> [x,fval,exitflag,output,lambda] = quadprog(H,f,A,b,[],[],lb)
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the default value of the optimality tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
x =
0.6667
1.3333
fval =
-8.2222
exitflag =
1
output =
包含以下字段的 struct:
message: 'Minimum found that satisfies the constraints.↵↵Optimization completed because the objective function is non-decreasing in ↵feasible directions, to within the default value of the optimality tolerance,↵and constraints are satisfied to within the default value of the constraint tolerance.↵↵Stopping criteria details:↵↵Optimization completed: The relative dual feasibility, 1.394658e-16,↵is less than options.OptimalityTolerance = 1.000000e-08, the complementarity measure,↵2.675395e-14, is less than options.OptimalityTolerance, and the relative maximum constraint↵violation, 1.480297e-16, is less than options.ConstraintTolerance = 1.000000e-08.↵↵Optimization Metric Options↵relative dual feasibility = 1.39e-16 OptimalityTolerance = 1e-08 (default)↵complementarity measure = 2.68e-14 OptimalityTolerance = 1e-08 (default)↵relative max(constraint violation) = 1.48e-16 ConstraintTolerance = 1e-08 (default)'
algorithm: 'interior-point-convex'
firstorderopt: 2.6645e-14
constrviolation: 0
iterations: 4
cgiterations: []
lambda =
包含以下字段的 struct:
ineqlin: [3×1 double]
eqlin: [0×1 double]
lower: [2×1 double]
upper: [2×1 double]
(5)有约束最小值优化
在有约束最优化问题中,通常要将该问题转换为更简单的子问题,对这些子问题可以求解并作为迭代过程的基础。早期的方法通常是通过构造惩罚函数等,将有约束的最优化问题转换为无约束最优化问题进行求解。现在,这些方法已经被更有效的基于K-T方程解的方法所取代。K-T方程是有约束最优化问题求解的必要条件。
MATLAB优化工具箱提供了fmincon函数用来计算有约束的最小值优化。
例:求函数![]() 的最小值,搜索的起始值为x = [10;10;10],同时目标函数中的变量要服从以下约束条件:
的最小值,搜索的起始值为x = [10;10;10],同时目标函数中的变量要服从以下约束条件:
![]()
function f = myfun3(x)
f = -x(1) * x(2) * x(3);
约束条件改写:
>> x0 = [10; 10; 10]; % 求解的起始点
A=[-1 -2 -2;1 2 2];
b=[0;72];
[x,fval] = fmincon(@myfun3,x0,A,b)
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the default value of the optimality tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
x =
24.0000
12.0000
12.0000
fval =
-3.4560e+03
>> A*x-b %对约束条件进行验证
ans =
-72.0000
-0.0000
(6)另外两种极小值优化问题
| 半无限问题 | fseminf |
|---|---|
| 0-1规划 | bintprog |
2、多目标优化
前面介绍的最优化方法只有一个目标函数,是单目标最优化方法。但是,在许多实际工程问题中,往往希望多个指标都达到最优值,所以就有多个目标函数,这种问题称为多目标最优化问题。
多目标规划有许多解法,下面列出常用的几种。
-
化多为少法:将多目标问题化成只有1个或2个目标的问题,然后用简单的决策方法求解。最常用的是线性加权和法。
-
分层序列法:将所有的目标按其重要程度依次排序,先求出第1个(最重要的)目标的最优解,然后在保证前一个目标最优解的前提下依次求下一个目标的最优解,一直求到最后一个目标为止。
-
直接求非劣解法:先求出一组非劣解,然后按事先确定好的评价标准从中找出一个满意的解。
-
目标规划法:当所有的目标函数和约束条件都是线性时,可以采用目标规划法,它是20世纪60年代初由查纳斯和库珀提出来的。此方法对每一个目标函数都事前给定一个期望值,然后在满足约束条件集合的情况下,找出使目标函数离期望值最近的解。
-
多属性效用法(MAUM):各个目标分别用各自的效用函数表示,然后构成多目标综合效用函数,以此来评价各个可行方案的优劣。
-
层次分析法:由T.沙基于1980年提出来。这种方法是通过对目标、约束条件、方案等的主观判断,对各种方案加以综合权衡比较,然后评定优劣。
-
重排次序法:把原来不好比较的非劣解,通过其他办法排出优劣次序。此外,还有多目标群决策和多目标模糊决策等方法。
针对多目标优化问题,MATLAB提供了fgoalattain和fminimax 函数用来进行求解。
例:
某工厂因生产需要欲采购一种原材料,市场上这种原材料有两个等级,甲级单价2元/千克,乙级单价1元/千克。要求所花总费用不超过200元,购得原材料总量不少于100千克,其中甲级原材料不少于50千克,问如何确定最好的采购方案。
设x1、x2分别为采购甲级和乙级原材料的数量(千克),要求总采购费用尽量少,总采购重量尽量多,采购甲级原材料尽量多。
function f=myfun4(x)
f(1)=2*x(1)+ x(2);
f(2)=-x(1)- x(2);
f(3)=-x(1);
>> goal=[200 -100 -50]; % 要达到的目标
weight=[2040 -100 -50]; % 各个目标的权重,多目标优化,比较主观,权重由自己设置
x0=[55 55]; % 搜索的初始值
% 约束条件
A=[2 1;-1 -1;-1 0];
b=[200 -100 -50];
lb=zeros(2,1);
% 调用fgoalattain函数进行多目标优化
[x,fval,attainfactor,exitflag] =...
fgoalattain(@myfun4,x0,goal,weight,A,b,[],[],lb,[])
Local minimum possible. Constraints satisfied.
fgoalattain stopped because the size of the current search direction is less than
twice the default value of the step size tolerance and constraints are
satisfied to within the default value of the constraint tolerance.
x =
50 50
fval =
150 -100 -50
attainfactor =
3.4101e-10
exitflag =
4
3、方程组求解
优化工具箱提供了3个方程求解的函数,其中,“\”算子可用于求解线性方程组Cx=d。当矩阵为n阶方阵时,采用高斯消元法进行求解;如果A不为方阵,则采用数值方法计算方程最小二乘意义上的解。fzero采用数值解法求解非线性方程,fsolve函数则采用非线性最小二乘算法求解非线性方程组。
例:求解下面方程组的根,其中包含两个未知数、两个方程。
方程组变换
function F = myfun5(x)
F = [2*x(1) - x(2) - exp(-x(1));
-x(1) + 2*x(2) - exp(-x(2))];
>> x0 = [-5; -5]; % 猜测的搜索初始值
options=optimset('Display','iter'); % 输出显示选项设置,显示出迭代过程
[x,fval] = fsolve(@myfun5,x0,options) % 调用fsolve命令
Norm of First-order Trust-region
Iteration Func-count f(x) step optimality radius
0 3 47071.2 2.29e+04 1
1 6 12003.4 1 5.75e+03 1
2 9 3147.02 1 1.47e+03 1
3 12 854.452 1 388 1
4 15 239.527 1 107 1
5 18 67.0412 1 30.8 1
6 21 16.7042 1 9.05 1
7 24 2.42788 1 2.26 1
8 27 0.032658 0.759511 0.206 2.5
9 30 7.03149e-06 0.111927 0.00294 2.5
10 33 3.29525e-13 0.00169132 6.36e-07 2.5
Equation solved.
fsolve completed because the vector of function values is near zero
as measured by the default value of the function tolerance, and
the problem appears regular as measured by the gradient.
x =
0.5671
0.5671
fval =
1.0e-06 *
-0.4059
-0.4059
4、最小二乘及数据拟合
最小二乘法是一种数学优化技术,它通过最小化误差的平方和找到一组数据的最佳函数匹配。最小二乘法通常用于曲线拟合。很多其他的优化问题也可以通过最小化能量或最大化熵用最小二乘形式表达。
MATLAB中提供了多个函数用来计算最小二乘问题,如\、lsqnonneg、lsqlin、lsqnonlin、lsqcurvefit等。
(方程的个数大于变量的个数)
求超定系统C·x = d的最小二乘解,约束条件为A·x≤b,lb≤x≤ub(具体的系数矩阵、边界条件如下所示)。
首先输入系数矩阵和上下边界。
>> C = [0.9501 0.7620 0.6153 0.4057
0.2311 0.4564 0.7919 0.9354
0.6068 0.0185 0.9218 0.9169
0.4859 0.8214 0.7382 0.4102
0.8912 0.4447 0.1762 0.8936];
d = [0.0578
0.3528
0.8131
0.0098
0.1388];
A =[0.2027 0.2721 0.7467 0.4659
0.1987 0.1988 0.4450 0.4186
0.6037 0.0152 0.9318 0.8462];
b =[0.5251
0.2026
0.6721];
lb = -0.1*ones(4,1);
ub = 2*ones(4,1);
% 然后调用约束最小二乘lsqlin函数:
>> [x,resnorm,residual,exitflag,output,lambda] = ...
lsqlin(C,d,A,b,[],[],lb,ub);
x,lambda.ineqlin,lambda.lower,lambda.upper % 查看计算的结果
Minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the default value of the optimality tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.
x =
-0.1000
-0.1000
0.2152
0.3502
ans =
0.0000
0.2392
0.0000
ans =
0.0409
0.2784
0.0000
0.0000
ans =
0
0
0
0
lambda结构数组中向量的非零元素可以说明解的主动约束条件。在本例中,第2个不等式约束和第1个、第2个下界边界约束是主动约束。
例:对下面的公式进行最小化优化。搜索的初始值为x = [0.3, 0.4]。
lsqnonlin函数用下面的向量值函数代替,其中k = 1:10 (因为 F 包含k个部分)。
![]()
function F = myfun6(x)
k = 1:10;
F = 2 + 2*k-exp(k*x(1))-exp(k*x(2));
>> x0 = [0.3 0.4] % 初始值
[x,resnorm] = lsqnonlin(@myfun6,x0) % 调用优化命令
x0 =
0.3000 0.4000
Local minimum possible.
lsqnonlin stopped because the size of the current step is less than
the default value of the step size tolerance.
x =
0.2578 0.2578
resnorm =
124.3622
第6节 模拟退火
函数需要连续,可求导
模拟退火算法(Simulated Annealing, SA)的思想借鉴于固体的退火原理,当固体的温度很高的时候,内能比较大,固体的内部粒子处于快速无序运动,当温度慢慢降低的过程中,固体的内能减小,粒子的慢慢趋于有序,最终,当固体处于常温时,内能达到最小,此时,粒子最为稳定。模拟退火算法便是基于这样的原理设计而成。
模拟退火算法过程(求最小值):
(1)随机挑选一个单元k,并给它一个随机的位移,求出系统因此而产生的能量变化ΔEk。
(2)若ΔEk⩽ 0,该位移可采纳,而变化后的系统状态可作为下次变化的起点;
若ΔEk>0,位移后的状态可采纳的概率为
式中T为温度,然后从(0,1)区间均匀分布的随机数中挑选一个数R,若R (3)转第(1)步继续执行,知道达到平衡状态为止。 MATLAB 工具箱中自带了模拟退火优化函数simulannealbnd 例: 蒙特卡罗方法(Monte Carlo method)也称统计模拟方法,是20世纪40年代中期由于科学技术的发展和电子计算机的发明,而被提出的以概率统计理论为指导的一类非常重要的数值计算方法,是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。蒙特卡罗方法的名字来源于摩纳哥的一个城市蒙特卡罗,该城市以赌博业闻名,而蒙特卡罗方法正是以概率为基础的方法。与蒙特卡罗方法对应的是确定性算法。 蒙特卡罗方法在金融工程学、宏观经济学、生物医学、计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算等)等领域应用的较为广泛。 当所求解的问题是某种随机事件出现的概率,或者是某个随机变量的期望值时,可通过某种“实验”的方法,以这种事件出现的频率估计这一随机事件的概率,或者得到这个随机变量的某些数字特征,并将其作为问题的解。有一个例子可以比较直观地了解蒙特卡罗方法:假设我们要计算一个不规则图形的面积,那么图形的不规则程度和分析性计算(比如积分)的复杂程度是成正比的。蒙特卡罗方法是怎么计算的呢?假想你有一袋豆子,把豆子均匀地朝这个图形上撒,然后数这个图形内外有多少颗豆子,计算豆子占所有豆子的比例,然后乘以撒豆子的总面积就是图形的面积。当豆子越小,撒得越多的时候,结果就越精确。在这里要假定豆子都在一个平面上,且相互之间没有重叠。 撒豆子——>统计 在解决实际问题的时候应用蒙特卡罗方法,主要有以下两部分工作。 通常蒙特卡罗方法通过构造符合一定规则的随机数,来解决数学上的各种问题。对于那些由于计算过于复杂而难以得到解析解或者根本没有解析解的问题,蒙特卡罗方法是一种有效的求出数值解的方法。一般蒙特卡罗方法在数学中最常见的应用就是蒙特卡罗积分。 首先使用均匀分布在边长为2的正方形面积内生成随机数,然后计算随机数落在圆内的比例,那么就可以得到圆占正方形面积的比例了。进而可以反推出圆周率,不过因为蒙特卡罗方法是一种随机方法,所以这个圆周率的误差比使用其他解析方法得到的结果误差要大很多。 因为rand函数生成的是1以内的均匀分布随机数,为了方便,这里只计算1/4圆的面积。相应的代码如下: 尝试不同的模拟点个数,观察结果变化情况 点越多,算出的结果越接近准确值 遗传算法(Genetic Algorithms)是基于生物进化理论的原理发展起来的一种广为应用的、高效的随机搜索与优化的方法。其主要特点是群体搜索策略和群体中个体之间的信息交换,搜索不依赖于梯度信息。它是20世纪70年代初期由美国密执根(Michigan)大学的霍兰(Holland)教授发展起来的。迄今为止,遗传算法是进化算法中最广为人知的算法。 遗传算法主要在复杂优化问题求解和工业工程领域应用,取得了一些令人信服的成果,所以引起了很多人的关注。遗传算法成功的应用包括:作业调度与排序、可靠性设计、车辆路径选择与调度、成组技术、设备布置与分配、交通问题,等等。 遗传算法具有以下几方面的特点。 遗传算法中的基本概念 遗传算法终止规则 遗传算法原理演示: 求解的最小值,x取值范围0~100之间的整数 第一代 第二代 第三代 通过三次迭代,可以找出最优解 MATLAB中的遗传算法函数: 约束条件如何写 nonlcon c ≤ 0 and ceq = 0 对上述条件写代码: 例: 在下列给定不等式约束和下边界条件约束下求MATLAB自带测试函数lincontest6 例: 将上面的遗传算法代码完成,求解(x − 50)^2 的最小值,x取值范围0~100之间的整数 要求每代4个个体 注意:不要设置随机种子,因为本身就要这种随机性 适用于离散问题,路径问题,旅行商问题等,没有标准的蚁群算法函数,需要改代码,很针对现实情况 旅行商问题(Traveling Saleman Problem,TSP)是车辆路径调度问题(VRP)的特例,由于数学家已证明TSP问题是NP难题,因此,VRP也属于NP难题。旅行商问题(TSP)又译为旅行推销员问题、货郎担问题,简称为TSP问题,是最基本的路线问题,该问题是在寻求单一旅行者由起点出发,通过所有给定的需求点之后,最后再回到原点的最小路径成本。 经典精确算法:穷举法、线性规划算法、动态规划算法、分支定界算法等运筹学中的传统算法,这些算法复杂度一般都很大,只适用于求解小规模问题。 近似算法:当问题规模较大时,其所需的时间成级数增长,这是我们无法接受的,算法求解问题的规模受到了很大的限制,一个很自然的想法就是牺牲精确解法中的最优性,去寻找一个好的时间复杂度我们可以容忍的,同时解的质量我们可以接受的算法.基于这一思想所设计出的算法统称为近似算法。如插入算法,最邻近算法等。 智能算法:随着科学技术和生产的不断发展,许多实际问题不可能在合理的时间范围内找到全局最优解,这就促使了近代最优化问题求解方法的产生。随着各种不同搜索机制的启发式算法相继出现,如禁忌搜索、遗传算法、模拟退火算法、人工神经网络、进化策略、进化编程、粒子群优化算法、蚁群优化算法和免疫计算等。 蚁群算法是受到对真实蚂蚁群觅食行为研究的启发而提出。生物学研究表明:一群相互协作的蚂蚁能够找到食物和巢穴之间的最短路径,而单只蚂蚁则不能。生物学家经过大量细致观察研究发现,蚂蚁个体之间的行为是相互作用相互影响的。蚂蚁在运动过程中,能够在它所经过的路径上留下一种称之为信息素的物质,而此物质恰恰是蚂蚁个体之间信息传递交流的载体。 随着时间推移,信息素会挥发,有蚂蚁走过,信息素会增加,p是挥发概率 终止条件 蚁群算法处理的都是离散问题(城市都是离散的),对于连续问题(比如求一个实数)很难操作,如果是一个实数,可参考的操作方式如下: 第一列:百位,第二列:十位,第三列:个位等。。。 第一次迭代结果: 最终结果: 图论起源于著名的柯尼斯堡七桥问题。一般认为,著名的数学家欧拉于1736年出版的柯尼斯堡七桥问题的论文是图论领域的第一篇文章。每座桥只走一次,然后回到远点。 图论(Graph theory)是数学的一个分支,它以图为研究对象,研究顶点和边组成的图形的数学理论和方法。图是区域在头脑和纸面上的反映,图论就是研究区域关系的学科。区域是一个平面,平面当然是二维的,但是,图在特殊的构造中,可以形成多维(例如大于3维空间)空间,这样的图已经超越了一般意义上的区域(例如一个有许多洞的曲面,它是多维的,曲面染色已经超出了平面概念)。 图论中的图是由若干给定的顶点及连接两顶点的边所构成的图形,这种图形通常用来描述某些事物之间的某种特定关系,用顶点代表事物,用连接两顶点的边表示相应两个事物间具有这种关系。 所有的点相连,边上的权重相加是最小的 MATLAB中的图像处理工具箱提供了一套全方位的标准算法和图形工具,用于进行图像处理、分析、可视化和算法开发。可用其对有噪图像或退化图像进行去噪或还原、增强图像以获得更高的清晰度、提取特征、分析形状和纹理,以及对两个图像进行匹配。工具箱中的大部分函数均以开放式MATLAB语言编写,这意味着可以检查算法、修改源代码和创建自定义函数。 图像处理工具箱在医学、机器视觉、遥感、监控、基因表达、显微镜技术、半导体测试、图像传感器设计、颜色科学及材料科学等领域,为工程师和科学家提供支持,同时也促进了图像处理技术的教学。 面临的问题有: 图像处理工具箱支持多种设备生成的图像,包括数码相机、图像采集系统、卫星和空中传感器、医学成像设备、显微镜、望远镜和其他科学仪器。用户可以用多种数据类型来可视化、分析和处理这些图像,包括单精度和双精度浮点和有符号或无符号的8、16和32位整数。 在MATLAB环境中,导入或导出图像进行处理的方式有几种。用户可以使用图像采集工具箱从Web 摄像头、图像采集系统、DCAM兼容相机和其他设备中采集实时图像。另外通过使用数据库工具箱,用户可以访问ODBC/JDBC兼容数据库中存储的图像。 MATLAB支持标准数据和图像格式,包括JPEG、TIFF、PNG、HDF、HDF-EOS、FITS、Microsoft Excel、ASCII和二进制文件等。它还支持多频带图像格式,如LANDSAT。同时MATLAB提供了低级I/O函数,可以让用户开发用于处理任何数据格式的自定义程序。图像处理工具箱支持多种专用图像文件格式。例如对于医学图像,它支持DICOM文件格式,包括关联的元数据,以及Analyze 7.5和Interfile格式。另外此工具箱还可以读取NITF格式的地理空间图像和HDR格式的高动态范围图像等。 图片的像素坐标: 在MATLAB中,使用函数imfinfo能够获得图像处理工具箱所支持的任何格式的图像文件的信息,其调用语法为: 在MATLAB中,可以使用函数translate来实现图像的平移。其调用语法为:SE2 = translate(SE,V)。其中,SE为一个模板,使用函数strel来创建,V是一个向量,用来指定平移的方向。 7、图像的镜像变换 图像的镜像变换分为两种:一种是水平镜像,另一种是垂直镜像。图像的水平镜像操作是将图像左半部分和右半部分以图像垂直中轴线为中心镜像进行变换,图像的垂直镜像操作是将图像上半部分和下半部分以图像水平中轴线为中心镜像进行变换。 对图像进行水平镜像和垂直镜像变换是通过对图像的像素数据做变换实现的。 使用函数fliplr和flipud对像素矩阵进行水平和垂直反转,就可以完成图像的镜像变换。 一般的方法是直接赋值为和它最相近的像素值,也可以通过一些插值算法来计算。后者处理的效果要好些,但是运算量也相应地会增加很多。MATLAB提供了imresize函数用于改变图像的尺寸。 旋转通常的做法是以图像的中心为圆心旋转。MATLAB提供了imrotate函数用于实现图像的旋转。 对于要处理的图像,用户可能只关心图像的一部分内容,而不是整个图像。如果对整个图像进行处理,不仅要花费大量的时间,而且图像的其他部分可能会影响处理的效果,所以这时就要剪切出所要关心的部分图像,这样可以大大地提高处理的效率。MATLAB提供了imcrop函数用来实现图像的剪切。 对比度增强是增强技术中的一种比较简单但又十分重要的方法。这种方法是按一定的规则逐点修改输入图像每一像素的灰度,从而改变图像灰度的动态范围。MATLAB提供了imadjust函数用来对图像的强度进行调整。 MATLAB提供了histeq函数通过直方图均衡化方法来增强对比度。 使用空域模板进行的图像处理,被称为空域滤波。模板本身被称为空域滤波器。按空域滤波处理的效果分类,可以分为平滑滤波器和锐化滤波器。平滑的目的在于消除混杂图像干扰,改善图像质量,强化图像表现特征。锐化的目的在于增强图像边缘,以便对图像进行识别和处理。 对图像中的每个像素进行3×3模板均值滤波,可以有效地平滑噪声。 MATLAB还提供了函数wiener2用于实现维纳滤波 (1)知道现值计算终值 (2)知道终值计算现值 内部收益率法(英文:Internal Rate of Return)是用内部收益率来评价项目投资财务效益的方法。 cf1:一年以后的钱 一年以后挣的钱/一年的利率=当前的价值 两年以后挣的钱/两年的利率=当前的价值 一般r是不知道的 123400:投资的钱,预计第一年挣:36200,第二年挣:54800,第三年挣:48100 列出公式之后,计算收益率 在机器学习和认知科学领域,人工神经网络(英文:artificial neural network,缩写ANN),简称神经网络(英文:neural network,缩写NN)或类神经网络,是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。神经网络由大量的人工神经元联结进行计算。大多数情况下人工神经网络能在外界信息的基础上改变内部结构,是一种自适应系统。现代神经网络是一种非线性统计性数据建模工具。 神经元:(对其进行加权求和) 单个神经元计算: 多个神经元计算: 多层网络的计算: 在图中每个圆圈都是一个神经元,每条线表示神经元之间的连接。分成了多层 输入层是知道的,输出层也是知道的,但是每一层中间的权重是不知道的 bp算法:反向传播,从右边依次向左调整权重,最终让整体误差最小,η:调整速率 最常用的函数:sigmoid 每一层里,神经元的个数并不是固定的,可以自己设置,神经元越多,拟合函数越复杂,所需要的计算时间也越多。如果层数过多,容易陷入局部最优。 选择拟合,也可以在命令行输入nftool,也可以在APPs中选 相关系数R越接近于1,效果越好 点击performance,训练次数越多,效果越好 点击save results,保存结果,最重要的结果就是net,接着可以在工作区中看到net对象,在命令行中输入net 通过上述的工具,生成代码,再对代码进行更改 利用上述工具,只能创建单层的神经网络 为了降低噪声、测量误差等带来的影响,也为了提高对未出现过的数据的预测能力,建议使用尽量少的隐含层层数。而单层结构可以使用有限的神经元个数拟合出任意有边界的分段连续函数。 支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解,是在分类与回归分析中分析数据的监督式学习模型与相关的学习算法。 线性分类: 将二维图改成三维图,用一个平面将两组点分开 Classification Learner使用演示 点开APPS——>classification learner 可以将并行计算的按钮关闭 除了可以导出模型,还可以导出代码 保存模型trainedModel 将导出的代码存为函数trainClassifier 元胞自动机是一种离散模型,在可计算性理论、数学及理论生物学都有相关研究。它是由无限个有规律、坚硬的方格组成,每格均处于一种有限状态。整个格网可以是任何有限维的。同时也是离散的。每格于t时的态由t-1时的一集有限格(这集叫那格的邻域)的态决定。每一格的“邻居”都是已被固定的。(一格可以是自己的邻居。)每次演进时,每格均遵从同一规矩一齐演进。 就形式而言,细胞自动机有三个特征: 康威生命游戏(Conway’s Game of Life),又称康威生命棋,是英国数学家约翰·何顿·康威在1970年发明的细胞自动机。 生命游戏中,对于任意细胞,规则如下: 可以把最初的细胞结构定义为种子,当所有在种子中的细胞同时被以上规则处理后,可以得到第一代细胞图。按规则继续处理当前的细胞图,可以得到下一代的细胞图,周而复始。 生命游戏是一个零玩家游戏。它包括一个二维矩形世界,这个世界中的每个方格居住着一个活着的或死了的细胞。一个细胞在下一个时刻生死取决于相邻八个方格中活着的或死了的细胞的数量。如果相邻方格活着的细胞数量过多,这个细胞会因为资源匮乏而在下一个时刻死去;相反,如果周围活细胞过少,这个细胞会因太孤单而死去。实际中,玩家可以设定周围活细胞的数目怎样时才适宜该细胞的生存。如果这个数目设定过高,世界中的大部分细胞会因为找不到太多的活的邻居而死去,直到整个世界都没有生命;如果这个数目设定过低,世界中又会被生命充满而没有什么变化。 实际中,这个数目一般选取2或者3;这样整个生命世界才不至于太过荒凉或拥挤,而是一种动态的平衡。这样的话,游戏的规则就是:当一个方格周围有2或3个活细胞时,方格中的活细胞在下一个时刻继续存活;即使这个时刻方格中没有活细胞,在下一个时刻也会“诞生”活细胞。 在这个游戏中,还可以设定一些更加复杂的规则,例如当前方格的状况不仅由父一代决定,而且还考虑祖父一代的情况。玩家还可以作为这个世界的“上帝”,随意设定某个方格细胞的死活,以观察对世界的影响。 在游戏的进行中,杂乱无序的细胞会逐渐演化出各种精致、有形的结构;这些结构往往有很好的对称性,而且每一代都在变化形状。一些形状已经锁定,不会逐代变化。有时,一些已经成形的结构会因为一些无序细胞的“入侵”而被破坏。但是形状和秩序经常能从杂乱中产生出来。 兰顿蚂蚁(英语:Langton’s ant)是细胞自动机的例子。它由克里斯托夫·兰顿在1986年提出,它由黑白格子和一只“蚂蚁”构成,是一个二维图灵机。兰顿蚂蚁拥有非常简单的逻辑和复杂的表现。在2000年兰顿蚂蚁的图灵完备性被证明。兰顿蚂蚁的想法后来被推广,比如使用多种颜色。 规则: 行为模式: 若从全白的背景开始,在一开始的数百步,蚂蚁留下的路线会出现许多对称或重复的形状,然后会出现类似混沌的假随机,至约一万步后会出现以104步为周期无限重复的“高速公路”朝固定方向移动。在目前试过的所有起始状态,蚂蚁的路线最终都会变成高速公路,但尚无法证明这是无论任何起始状态都会导致的必然结果。 Statistics and Machine Learning Toolbox™ 提供用来描述、分析数据和对数据建模的函数和应用程序。可以使用用于探查数据分析的描述性统计和绘图,使用概率分布拟合数据,生成用于 Monte Carlo 仿真的随机数,以及执行假设检验。回归和分类算法用于依据数据执行推理并构建预测模型。 对于多维数据分析,Statistics and Machine Learning Toolbox 提供特征选择、逐步回归、主成分分析 (PCA)、正则化和其他降维方法,从而确定影响模型的变量或特征。 该工具箱提供了受监督和无监督机器学习算法,包括支持向量机 (SVM)、促进式 (boosted) 和袋装 (bagged) 决策树、k-最近邻、k-均值、k-中心点、分层聚类、高斯混合模型和隐马尔可夫模型。许多统计和机器学习算法可以用于大到无法在内存中存储的数据集的计算。 (1)MATLAB机器学习工具箱支持的数据有: (2)MATLAB机器学习工具箱不支持的数组有: (3)数据类型举例: (4)数据有缺值的情况处理: 在实际运用机器学习相关分析时,数据难免会有缺失的情况。这种时候一般用NaN来代替相应的数据,这样可以保留原始数据的结构。如果要删除某些具有NaN数值的行,那么会把一些有用的数据可能也删掉了。 matlab提供了一些函数,可以支持NaN: 载入测试数据 将病人按照年龄分类别 查验一下效果 改为类别类型会丢失一些信息,但可能会更方便些。 将体重分为四个级别 查验结果 根据分类进行统计 有输入有输出 具体执行步骤: 1)数据准备 一般准备好一个数组X,每行是一个样本,每列是一个变量,或者predictor。缺失值使用NaN代替。响应数据一般定义为Y。对于回归来说,Y必须是数值型。对于分类来说,各种数据类型均支持。 2)选择算法 权衡各种算法优缺点,选择合适的算法。 需要考虑的因素有: 3)训练模型 4)验证方法选择 5)模型改进 6)预测 机器学习中,决策树是一个预测模型;他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表某个可能的属性值,而每个叶节点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。 数据挖掘中决策树是一种经常要用到的技术,可以用于分析数据,同样也可以用来作预测。 信息熵是用来衡量一元模型中信息不确定性的指标。信息的不确定性越大,熵的值也就越大。而影响熵值的主要因素是概率。这里所说的一元模型就是指单一事件,而不确定性是一个事件出现不同结果的可能性。 例如抛硬币,可能出现的结果有两个,分别是正面和反面。而每次抛硬币的结果是一个非常不确定的信息。因为根据我们的经验或者历史数据来看,一个均匀的硬币出现正面和反面的概率相等,都是50%。因此很难判断下一次出现的是正面还是反面。这时抛硬币这个事件的熵值也很高。而如果历史数据告诉我们这枚硬币在过去的100次试验中99次都是正面,也就是说这枚硬币的质量不均匀,出现正面结果的概率很高。那么我们就很容易判断下一次的结果了。这时的熵值很低,只有0.08。 我们把抛硬币这个事件看做一个随机变量S,它可能的取值有2种,分别是正面x1和反面x2。每一种取值的概率分别为P1和P2。我们要获得随机变量S的取值结果至少要进行1次试验,试验次数与随机变量S可能的取值数量(2种)的对数函数Log有联系。Log2=1(以2为底)。因此熵的计算公式是: 条件熵是通过获得更多的信息来消除一元模型中的不确定性。也就是通过二元或多元模型来降低一元模型的熵。我们知道的信息越多,信息的不确定性越小。 例如,只使用一元模型时我们无法根据用户历史数据中的购买频率来判断这个用户本次是否也会购买。因为不确定性太大。在加入了促销活动,商品价格等信息后,在二元模型中我们可以发现用户购买与促销活动,或者商品价格变化之间的联系。并通过购买与促销活动一起出现的概率,和不同促销活动时购买出现的概率来降低不确定性。 确定哪个条件是放在最上面的。 互信息是用来衡量信息之间相关性的指标。当两个信息完全相关时,互信息为1,不相关时为0。在前面的例子中用户购买与促销活动这两个信息间的相关性究竟有多高,我们可以通过互信息这个指标来度量。具体的计算方法就熵与条件熵之间的差。用户购买的熵E(T)减去促销活动出现时用户购买的熵E(T,X)。 例1: 判别分析是一种有监督学习,最简单的情况是LDA,即限行判别分析。 例如需要解决以下的分类问题。 但平均值的差有其缺点: 所以希望同时引入对集中程度的评价,相当于方差: 最终的评价指标为: 示例: 贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。这里就来介绍贝叶斯定理以及贝叶斯分类中最简单的一种:朴素贝叶斯分类。 一个简单例子: 一个班级有300个女生,200个男生 P(女)=300/500=0.6 P(男)=200/500=0.4 载入测试数据: 训练朴素贝叶斯分类器: 构造测试数据: 预测: 结果绘图: 分别绘图: 属于有监督的机器学习,是分类方法。 最邻近分类模型属于“基于记忆”的非参数局部模型,这种模型并不是立即利用训练数据建立模型,数据也不再被函数和参数所替代。在对测试样例进行类别预测的时候,找出和其距离最接近的k个样例,以其中数量最多的类别作为该样例的类预测结果。 在黑色实线圈内,红色点多,所以绿色点归类到红色这一类 一般圈内都是奇数,这样就不存在红色的点和蓝色的点一样多了 欧式距离: 曼哈顿距离: 切比雪夫距离: 一个主要的缺点:如果距离计算中的各变量测量尺度不同,那么距离的计算会有相当大的影响。 可能的一个解决办法:归一化 一个例子,贷款违约率: 例1: 还可以选用其他距离计算方法: 预测: 例2: 如何对一个点进行分类的: 画一个新点: 训练一个Kd-tree搜索模型: 搜索新点周围最近的10个点: 查看10个临近点的种类: 属于无监督的机器学习 聚类分析(英语:Cluster analysis,亦称为群集分析)是对于统计数据分析的一门技术,在许多领域受到广泛应用,包括机器学习,数据挖掘,模式识别,图像分析以及生物信息。聚类是把相似的对象通过静态分类的方法分成不同的组别或者更多的子集(subset),这样让在同一个子集中的成员对象都有相似的一些属性,常见的包括在坐标系中更加短的空间距离等。 一般把数据聚类归纳为一种非监督式学习。 Statistics and Machine Learning Toolbox 包括用于执行聚类分析的算法,通过根据相似度测量对数据分组来发现数据集中的规律。可用的算法包括 k-均值、k-中心点、分层聚类、高斯混合模型和隐马尔可夫模型。当不知道聚类的数量时,可以使用聚类评估技术根据特定指标确定数据中存在的聚类数量。 假设有N个待聚类的样本,对于层次聚类来说,步骤: 整个聚类过程其实是建立了一棵树,在建立的过程中,可以通过在第二步上设置一个阈值,当最近的两个类的距离大于这个阈值,则认为迭代可以终止。另外关键的一步就是第三步,如何判断两个类之间的相似度有不少种方法。这里介绍一下三种: 使用linkage函数计算分层聚类树 横轴:第几个样本 纵轴:两个样本点之间的距离(上图指定的是切比雪夫距离) 查看结果系统树图 K平均算法需要输入待聚类的数据和欲聚类的簇数k,主要的聚类过程有3步: 原始数据绘图 K平均算法进行聚类 对新值进行计算 结果绘图 GMM和k-means其实是十分相似的,区别仅仅在于对GMM来说,我们引入了概率。 GMM将求解分为两步:第一步是假设我们知道各个高斯模型的参数(可以初始化一个,或者基于上一步迭代结果),去估计每个高斯模型的权值;第二步是基于估计的权值,回过头再去确定高斯模型的参数。重复这两个步骤,直到波动很小,近似达到极值。 创建高斯混合模型数据 拟合高斯混合模型 聚类结果绘图 回归:连续的,并不是离散的分类,有监督的学习 回归分析(Regression Analysis)是一种统计学上分析数据的方法,目的在于了解两个或多个变量间是否相关、相关方向与强度,并建立数学模型以便观察特定变量来预测研究者感兴趣的变量。一般来说,通过回归分析我们可以由给出的自变量估计因变量的条件期望。 回归分析是建立因变量Y与自变量X之间关系的模型。 在统计学中,线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。 线性回归的模型: 拟合方法选择: 最小二乘法 fitlm函数使用最小二乘法进行拟合。这种方法在很确定模型的形式的时候非常好用,就是只需要寻找参数的情况下。这种方法需要用户人工检查数据中的异常值并剔除。而异常值的检验办法是通过残差分析来实现。 稳定回归 fitlm函数中如果添加了RobustOpts参数对,那么就可以进行稳定回归了。稳定回归方法可以省去人工检测异常值的步骤,但是step函数不能适用于稳定回归方法。 逐步回归 使用逐步回归函数stepwiselm可以从一个模型出发,尝试增加或者减少一项,从而改进结果,知道无法改进为止。 准备数据: predictor data X 行:observation --样本 列:predictor --变量 response data Y 有两种数据输入格式: 对于table数组来说,通过以下方式指定response: 一般数组形式: 例:数组的创建 选择设置具体拟合模型的方法有三种: (a)简称: constant:常数,linear:各项直接相加,purequadratic:平方项, fitlm函数默认模型是 ‘linear’ stepwiselm函数默认起始模型是’constant’,上限模型是’interactions’ 调用格式举例: (b)公式: ‘Y ~ terms’ 例如: 举例: (c)项目数组 通过一个矩阵数组来指定方程的形式,数组的每一行表示一项,每一列表示一个predictor变量,最后再加一列,一般指的是response变量 如果输入输出变量是table格式: 如果更改了table数组的每列顺序: 如果输入输出变量是矩阵数组格式: 如果使用的是stepwiselm函数: 从最简单的模型开始尝试,逐步回归,如下例子,最简单是[0 0 0],最复杂的是T 自动寻找最合适的相关模型,做拟合 绿色线是预测的油耗 上下是95%的置信区间 有三种方法可以用来使用得到的模型进行预测的方法: 缺点是:不可以返回置信区间,一般都用predict 提供模型显示信息 提供模型定义和参数 如果数据有有类别格式的 70年是B2 * 0 先使用相等的权重进行回归计算,第二代将误差较大的点对应的权重调低,然后再进行回归计算。 查看异常值的权重 而权重中位数为 检查结果 排除异常值 预测 预测 Mathworks在R2016a中正式推出了GUIDE的替代产品:AppDesigner, 这是在MATLAB图形系统转向使用面向对象系统之后(2014b),一个重要的后续产品,它旨在顺应Web的潮流,帮助用户利用新的图形系统方便的设计更加美观的GUI。 3、具体代码操作 下面我们来演示如何使用app designer 调用App Designer,只需要在命令行中输入appdesigner就可以了 或者在工具栏中选择新建>app>app designer,也可以打开一个appdesigner的窗口。 邻里成分分析(Neighbourhood components analysis,Nca)是一种监督式学习的方法,根据一种给定的距离度量算法对样本数据进行度量,然后对多元变量数据进行分类。在功能上其和k近邻算法的目的相同,直接利用随机近邻的概念确定与测试样本临近的有标签的训练样本。 邻里成分分析是一种距离度量学习方法,其目的在于通过在训练集上学习得到一个线性空间转移矩阵,在新的转换空间中最大化平均留一(LOO)分类效果。该算法的关键是与空间转换矩阵相关的的一个正定矩阵A,该矩阵A可以通过定义A的一个可微的目标函数并利用迭代法(如共轭梯度法、共轭梯度下降法等)求解得到。该算法的好处之一是类别数K可以用一个函数f(确定标量常数)来定义。因此该算法可以用来解决模型选择的问题。 MATLAB 提供了fscnca和fsrnca两个函数进行邻里成分分析。 fscnca:特征选择分类 fsrnca:特征选择回归 创建测试数据 调用fscnca函数进行分类 绘制特征选择的权重数据,不相关特征的权重会非常接近于0 从图中可以看出,3,9,15是异常的,刚好对应上一开始更改的数据 添加100个不相关的特征 使用nca模型进行拟合 绘制特征权重结果图 所有的权重都接近于0,说明使用的lambda太大了。如果lambda趋近于无穷大,那么所有的特征权重就会趋近于0. 下面使用五折交叉验证来调节lambda。 对于n个样本来说,最佳的lambda可以最小化NCA模型的误差,一般的话会是1/n的倍数。 针对不同的lambda绘制平均损失值 选择得到最佳的lambda数值 使用最佳的lambda数值拟合nca模型 绘制新的特征权重 fsrnca函数使用nca对回归问题进行特征选择 绘制特征权重信息>> dejong5fcn % 需要优化的测试函数
>> dejong5fcn % 优化测试函数
>> fun = @dejong5fcn; % 目标函数
>> [x,fval] = simulannealbnd(fun,[0 0]) % 目标函数、初始点
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-32.0285 -0.1280
fval =
10.7632
>> % 如果有绘图
options = saoptimset('PlotFcns',{@saplotbestx,@saplotbestf,@saplotx,@saplotf});
% 最优解,最优函数值,当前点,当前函数值
>> % 如果有上下限约束
x0 = [0,0];
lb = [-64,-64];
ub = [64,64];
x = simulannealbnd(fun,x0,lb,ub,options)
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-31.9797 -31.9777
% 多次运行发现,会出现不同的结果,所以多运行几次,选结果最好的那个就可以了
>> [x,fval] = simulannealbnd(fun,[0 0])
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-31.9808 -31.9728
fval =
0.9980
>> [x,fval] = simulannealbnd(fun,[0 0])
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
16.0012 -31.9608
fval =
3.9683
>> [x,fval] = simulannealbnd(fun,[0 0])
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
0 0
fval =
12.6705
>> [x,fval] = simulannealbnd(fun,[0 0])
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-31.8048 -31.9290
fval =
0.9981
% 求:min f(x) = (4 - 2.1*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-4 + 4*x2^2)*x2^2;
% 写成函数形式
function y = simple_objective(x)
y = (4 - 2.1*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-4 + 4*x(2)^2)*x(2)^2;
>> ObjectiveFunction = @simple_objective; % 创建函数句柄
>> X0 = [0.5 0.5]; % 初始点
>> [x,fval,exitFlag,output] = simulannealbnd(ObjectiveFunction,X0)
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-0.0900 0.7128
fval =
-1.0316
exitFlag =
1
output =
包含以下字段的 struct:
iterations: 1223
funccount: 1232
message: 'Optimization terminated: change in best function value less than options.FunctionTolerance.'
rngstate: [1×1 struct]
problemtype: 'unconstrained'
temperature: [2×1 double]
totaltime: 0.3595
>> % 如果有上下限约束
lb = [-64 -64];
ub = [64 64];
[x,fval,exitFlag,output] = simulannealbnd(ObjectiveFunction,X0,lb,ub);
Optimization terminated: change in best function value less than options.FunctionTolerance.
>> fprintf('The number of iterations was : %d\n', output.iterations);
fprintf('The number of function evaluations was : %d\n', output.funccount);
fprintf('The best function value found was : %g\n', fval);
The number of iterations was : 2386 迭代次数
The number of function evaluations was : 2405
The best function value found was : -1.03163 最佳值
>> x
x =
0.0897 -0.7129
% 求:min f(x) = (a - b*x1^2 + x1^4/3)*x1^2 + x1*x2 + (-c + c*x2^2)*x2^2;
% 这是个带参数的函数
% 写成函数形式
function y = parameterized_objective(x,a,b,c)
y = (a - b*x(1)^2 + x(1)^4/3)*x(1)^2 + x(1)*x(2) + (-c + c*x(2)^2)*x(2)^2;
>> a = 4; b = 2.1; c = 4; % define constant values
ObjectiveFunction = @(x) parameterized_objective(x,a,b,c);
>> X0 = [0.5 0.5];
[x,fval] = simulannealbnd(ObjectiveFunction,X0)
Optimization terminated: change in best function value less than options.FunctionTolerance.
x =
-0.0899 0.7127
fval =
-1.0316
第7节 蒙特卡罗算法
用蒙特卡罗方法模拟某一过程时,需要产生各种概率分布的随机变量。
用统计方法把模型的数字特征估计出来,从而得到实际问题的数值解。
>> A=rand(1000,1000);
B=rand(1000,1000);
C=sqrt(A.^2+B.^2); % 点到原点的距离
D=logical(C<=1); % 若<=1,说明在圆内
F=sum(D(:));
mypi=F/numel(A)*4 % 计算pi,其中numel(A)为A中的元素个数
mypi =
3.1404
>> clear
for n=10:20:1000
A=rand(n,n);
B=rand(n,n);
C=sqrt(A.^2+B.^2);
D=logical(C<=1);
F=sum(D(:));
mypi=F/numel(A)*4; % 计算pi,其中numel(A)为A中的元素个数
plot(A(D),B(D),'r.')
hold on
plot(A(~D),B(~D),'b.')
hold off
axis square
title(['总点数 =' num2str(n*n) ' and my pi = ' num2str(mypi)])
drawnow
end
>> X=12*rand(1000,1000)-6; % 因为rand生成的是0-1之间的随机数,*12-6后的区间为【-6,6】
Y=12*rand(1000,1000)-6;
C1=sqrt(X.^2/9+Y.^2/36);
C2=sqrt(X.^2/36+Y.^2);
C3=sqrt((X-2).^2/9+(Y+1).^2/9);
D1=logical(C1<=1);
D2=logical(C2<=1);
D3=logical(C3<=1);
D=D1&D2&D3;
F=sum(D(:));
area_shade=F/numel(X)*12*12 %阴影个数/总个数=比例,比例*总面积=阴影面积
area_shade =
7.2072
第8节 遗传算法
>> objfun=@(x)(x-50).^2
x=0:100;
y=(x-50).^2;
plot(x,y)
objfun =
包含以下值的 function_handle:
@(x)(x-50).^2
>> rng(0) %设置随机种子
>> c=randperm(100,4)' % 100以内的整数随机选择四个
c =
82
90
13
89
>> str = dec2bin(c) % 二进制编码
str =
4×7 char 数组 '1010010'
'1011010'
'0001101'
'1011001'
>> %%%% 选择
idx_choose=reshape(randperm(4),2,2) % 随机生成数组,并转化成2行2列
idx_choose =
2 4
3 1
% 将第一列放在一起,第二列放在一起
>> cp1=str(idx_choose(:,1),:) % 选择配对1
cp2=str(idx_choose(:,2),:) % 选择配对2
cp1 =
2×7 char 数组
'1011010'
'0001101'
cp2 =
2×7 char 数组
'1011001'
'1010010'
>> % 单点交叉,交叉点生成,选择交叉点,可以用随机数生成交叉点,也可以指定
% cros_p1=randperm(6,1)
% cros_p2=randperm(6,1)
cros_p1=5;
cros_p2=4;
>> %%%% 交叉
cp1_new=[cp1(1,1:cros_p1) cp1(2,cros_p1+1:end);
cp1(2,1:cros_p1) cp1(1,cros_p1+1:end);]
cp1_new = % 第一行与第二行的前五个数不变,后两个数交换了
2×7 char 数组
'1011001'
'0001110'
>> bin2dec(cp1) % 原始数据 将二进制转换为十进制
bin2dec(cp1_new) % 新数据
ans =
90
13
ans =
89
14
>> cp2_new=[cp2(1,1:cros_p2) cp2(2,cros_p2+1:end);
cp2(2,1:cros_p2) cp2(1,cros_p2+1:end);]
cp2_new = % 第一行与第二行的前四个数不变,后三个数交换了
2×7 char 数组
'1011010'
'1010001'
>> bin2dec(cp2) % 原始数据
bin2dec(cp2_new) % 新数据
ans =
89
82
ans =
90
81
>> str_new=[cp1_new; %组合新生成的数
cp2_new]
str_new =
4×7 char 数组
'1011001'
'0001110'
'1011010'
'1010001'
>> bin2dec(str_new)
ans =
89
14
90
81
>> %%%% 变异,一般变异概率都是很小的
if str_new(15)=='1'
str_new(15)='0';
else
str_new(15)='1';
end
>> str_new
str_new =
4×7 char 数组
'1011001'
'0001110'
'1010010'
'1010001'
>> c_new=bin2dec(str_new)
c_new =
89
14
82
81
>> c_alltemp=[c;c_new]
c_alltemp =
82
90
13
89
89
14
82
81
>> b=objfun(c_alltemp)
b =
1024
1600
1369
1521
1521
1296
1024
961
>> [bbest,idx_b]=sort(b) % 排序,找到最小的值
bbest =
961
1024
1024
1296
1369
1521
1521
1600
idx_b =
8
1
7
6
3
4
5
2
>> c_1=c % 保存历史数据
c_1 =
82
90
13
89
>> c=c_alltemp(idx_b(1:4)) %保留出下标排名前四的最小的四个数据
c =
81
82
82
14
>> str = dec2bin(c)
str =
4×7 char 数组
'1010001'
'1010010'
'1010010'
'0001110'
>> idx_choose= [ 2 3
1 4]
idx_choose =
2 3
1 4
>> cp1=str(idx_choose(:,1),:) % 选择配对1
cp2=str(idx_choose(:,2),:) % 选择配对2
cp1 =
2×7 char 数组
'1010010'
'1010001'
cp2 =
2×7 char 数组
'1010010'
'0001110'
>> %%%% 交叉
cp1_new=[cp1(1,1:cros_p1) cp1(2,cros_p1+1:end);
cp1(2,1:cros_p1) cp1(1,cros_p1+1:end);]
bin2dec(cp1) % 原始数据
bin2dec(cp1_new) % 新数据
cp1_new =
2×7 char 数组
'1010001'
'1010010'
ans =
82
81
ans =
81
82
>> cp2_new=[cp2(1,1:cros_p2) cp2(2,cros_p2+1:end);
cp2(2,1:cros_p2) cp2(1,cros_p2+1:end);]
bin2dec(cp2) % 原始数据
bin2dec(cp2_new) % 新数据
cp2_new =
2×7 char 数组
'1011110'
'0000010'
ans =
82
14
ans =
94
2
>> str_new=[cp1_new;
cp2_new]
bin2dec(str_new)
str_new =
4×7 char 数组
'1010001'
'1010010'
'1011110'
'0000010'
ans =
81
82
94
2
>> %%%% 变异,变异位置理论上来说不是指定的,而是随机生成的,此处为了看演示效果,直接指定
if str_new(9)=='1'
str_new(9)='0';
else
str_new(9)='1';
end
str_new
str_new =
4×7 char 数组
'1000001'
'1010010'
'1011110'
'0000010'
>> c_new=bin2dec(str_new)
c_new =
65
82
94
2
>> c_alltemp=[c;c_new]
c_alltemp =
81
82
82
14
65
82
94
2
>> b=objfun(c_alltemp)
b =
961
1024
1024
1296
225
1024
1936
2304
>> [bbest,idx_b]=sort(b)
bbest =
225
961
1024
1024
1024
1296
1936
2304
idx_b =
5
1
2
3
6
4
7
8
>> c_2=c % 保存历史数据
c_2 =
81
82
82
14
>> c=c_alltemp(idx_b(1:4)) % 选出这一代中最适应环境的四个数
c =
65
81
82
82
>> str = dec2bin(c)
idx_choose= [ 2 3
1 4]
cp1=str(idx_choose(:,1),:) % 选择配对1
cp2=str(idx_choose(:,2),:) % 选择配对2
% 单点交叉,交叉点生成
% cros_p1=randperm(6,1)
% cros_p2=randperm(6,1)
cros_p1=5;
cros_p2=2;
%%%% 交叉
cp1_new=[cp1(1,1:cros_p1) cp1(2,cros_p1+1:end);
cp1(2,1:cros_p1) cp1(1,cros_p1+1:end);]
bin2dec(cp1) % 原始数据
bin2dec(cp1_new) % 新数据
cp2_new=[cp2(1,1:cros_p2) cp2(2,cros_p2+1:end);
cp2(2,1:cros_p2) cp2(1,cros_p2+1:end);]
bin2dec(cp2) % 原始数据
bin2dec(cp2_new) % 新数据
str_new=[cp1_new;
cp2_new]
bin2dec(str_new)
%%%% 变异
if str_new(3)=='1'
str_new(3)='0';
else
str_new(3)='1';
end
if str_new(7)=='1'
str_new(7)='0';
else
str_new(7)='1';
end
str_new
c_new=bin2dec(str_new)
c_alltemp=[c;c_new]
b=objfun(c_alltemp)
[bbest,idx_b]=sort(b)
c_3=c % 保存历史数据
c=c_alltemp(idx_b(1:4))
str =
4×7 char 数组
'1000001'
'1010001'
'1010010'
'1010010'
idx_choose =
2 3
1 4
cp1 =
2×7 char 数组
'1010001'
'1000001'
cp2 =
2×7 char 数组
'1010010'
'1010010'
cp1_new =
2×7 char 数组
'1010001'
'1000001'
ans =
81
65
ans =
81
65
cp2_new =
2×7 char 数组
'1010010'
'1010010'
ans =
82
82
ans =
82
82
str_new =
4×7 char 数组
'1010001'
'1000001'
'1010010'
'1010010'
ans =
81
65
82
82
str_new =
4×7 char 数组
'1010001'
'1000001'
'0110010'
'1010010'
c_new =
81
65
50
82
c_alltemp =
65
81
82
82
81
65
50
82
b =
225
961
1024
1024
961
225
0
1024
bbest =
0
225
225
961
961
1024
1024
1024
idx_b =
7
1
6
2
5
3
4
8
c_3 =
65
81
82
82
c =
50
65
65
81
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)
% 函数,变量个数,等式约束,不等式约束,上下限约束,非线性约束,参数设置
[x,fval,exitflag,output,population,scores] = ga(...)
![]()
![]()
function [c ceq] = nlinconst(x)
% 加冒号,写成数组相乘的形式,加快计算速度,而不是用循环
c(:,1) = x(:,1).^2/4 + x(:,2).^2/9 + x(:,3).^2/25 - 6;
c(:,2) = cosh(x(:,1) + x(:,2)) - x(:,3);
ceq = x(:,1).*x(:,2).*x(:,3) - 2;
![]() 的最小值
的最小值>> A = [1 1; -1 2; 2 1]; % 线性不等式约束条件
b = [2; 2; 3]; % 线性不等式约束条件
lb = zeros(2,1); % 边界约束
[x,fval,exitflag] = ga(@lincontest6,2,A,b,[],[],lb) % 2代表有两个变量
Optimization terminated: average change in the fitness value less than options.FunctionTolerance.
x =
0.6670 1.3340
fval =
-8.2258
exitflag =
1
clear
objfun=@(x)(x-50).^2;
c=randperm(100,4)'; % 随机生成的初始解,如果是个位数,转换成二进制,不一定是7列
best_result=[];
c_result=[];
str00=['0';'0';'0';'0'];
for iter=1:100 % 终止条件是最大迭代次数是100次
str = dec2bin(c); % 转换为二进制
while size(str,2)<7 % 如果列数小于7
str=[str00 str]; % 通过循环补为7列
end
%%%% 选择
idx_choose=reshape(randperm(4),2,2);
cp1=str(idx_choose(:,1),:); % 选择配对1
cp2=str(idx_choose(:,2),:); % 选择配对2
% 单点交叉,交叉点生成
cros_p1=randperm(length(cp2)-1,1);
cros_p2=randperm(length(cp2)-1,1);
%%%% 交叉
cp1_new=[cp1(1,1:cros_p1) cp1(2,cros_p1+1:end);
cp1(2,1:cros_p1) cp1(1,cros_p1+1:end);];
cp2_new=[cp2(1,1:cros_p2) cp2(2,cros_p2+1:end);
cp2(2,1:cros_p2) cp2(1,cros_p2+1:end);];
str_new=[cp1_new;
cp2_new];
%%%% 变异
n_mute=randperm(numel(str_new),1); % 每次随机 选其中一个基因变异,变异的概率是1/28
if str_new(n_mute)=='1'
str_new(n_mute)='0';
else
str_new(n_mute)='1';
end
c_new=bin2dec(str_new);
c_alltemp=[c;c_new];
b=objfun(c_alltemp);
[bbest,idx_b]=sort(b);
best_result(iter)=bbest(1);
c_result=[c_result c]; % 保存历史数据
c=c_alltemp(idx_b(1:4));
% if all(diff(c)==0) % 所有个体相同的时候终止迭代
% break
% end
end
best_result % 历史最优值
c_result % 历史个体
c % 最终代个体
第9节 蚁群算法
% 蚁群算法示例程序
clc;
clear;
close all;
%% 初始数据输入
x=[82 91 12 92 63 9 28 55 96 97 15 98 96 49 80 14 42 92 80 96]; % 坐标点x坐标
y=[66 3 85 94 68 76 75 39 66 17 71 3 27 4 9 83 70 32 95 3]; % 坐标点y坐标
% x=[1304,3639,4177,3712,3488,3326,3238,4196,4312,4386,3007,2562,2788,2381,1332,3715,3918,4061,3780,3676,4029,4263,3429,3507,3394,3439,2935,3140,2545,2778,2370];
% y=[2312,1315,2244,1399,1535,1556,1229,1004,790,570,1970,1756,1491,1676,695,1678,2179,2370,2212,2578,2838,2931,1908,2367,2643,3201,3240,3550,2357,2826,2975];
[X1,X2]=meshgrid(x,x); %生成网格数据
[Y1,Y2]=meshgrid(y,y);
D=sqrt((X1-X2).^2+(Y1-Y2).^2); % 两点之间距离
N=numel(x); % 一共有多少个城市
MaxIt=300; % 最大迭代次数
nAnt=40; % 蚂蚁的个数(种群数量)
tau=ones(N,N); % 初始信息素
eta=1./D; % 启发因子矩阵,也就是距离的倒数,用于对转移概率的修正。不仅依靠信息素,也可以引入距离信息
rho=0.05; % 挥发率,太小速度会很慢,太大会陷入局部最优,需要小,但是不能特别小
Tour=zeros(nAnt,N);% 用于记录路径,得到40行,20列数组(40是蚂蚁的个数)
Cost=zeros(nAnt,1);% 用于记录路径总长度
BestCost=inf; % 全局最优的路径长度,初始值定义为最大
BestCostALL=Inf(MaxIt,1); % 每次迭代最优的路径的长度
for iter=1:MaxIt % 迭代次数 所有蚂蚁同时出发,所有都走完一圈回来了,再同时出发
for kAntID=1:nAnt % 每个蚂蚁分别计算
Tour(kAntID,1)=randi([1 N]); % 1到N之间的任意一个整数,作为起始点
for itourcity=2:N % 需要走的城市路径下标,因为第一个已经有了,所以这里从2开始编号
lastcityID=Tour(kAntID,itourcity-1); % 提取出上一个城市的值
P=tau(lastcityID,:).*eta(lastcityID,:);% 转移概率
P(Tour(kAntID,1:itourcity-1))=0; % 禁忌表,已经走过的概率设置为0
P=P/sum(P); % 归一化
r=rand; % 生成一个随机数
C=cumsum(P); %概率累加求和
j=find(r<=C,1); % 根据之前概率分布随机选择一个城市
Tour(kAntID,itourcity)=j; % 记录蚂蚁走过的城市
end
Ttemp=[Tour(kAntID,:)' Tour(kAntID,[2:end 1])']; % 当前蚂蚁各段路径的起点终点
L=0; % 总路径长度初始值
for i=1:N
L=L+D(Ttemp(i,1),Ttemp(i,2)); % 将各段路径长度加起来
end
Cost(kAntID)=L; % 总的路径长度
if Cost(kAntID)Iteration 1: Best Cost = 557.469
% 中间的绘图程序
function PlotSolution(tour,x,y)
tour=[tour tour(1)];
plot(x(tour),y(tour),'k-o',...
'MarkerSize',10,...
'MarkerFaceColor','y',...
'LineWidth',1.5);
xlabel('x');
ylabel('y');
axis equal;
grid on;
alpha = 0.1;
xmin = min(x);
xmax = max(x);
dx = xmax - xmin;
xmin = floor((xmin - alpha*dx)/10)*10;
xmax = ceil((xmax + alpha*dx)/10)*10;
xlim([xmin xmax]);
ymin = min(y);
ymax = max(y);
dy = ymax - ymin;
ymin = floor((ymin - alpha*dy)/10)*10;
ymax = ceil((ymax + alpha*dy)/10)*10;
ylim([ymin ymax]);
end
第10节 图论
1、图的创建
(1)无向图
>> figure
>> G = graph([1 1],[2 3]) % 创建
G =
graph - 属性:
Edges: [2×1 table]
Nodes: [3×0 table]
>> G.Edges % 边
ans =
2×1 table
EndNodes
________
1 2
1 3
>> plot(G)
>> G.Nodes.Name = {'A' 'B' 'C'}'; % 节点名称
>> G.Edges
ans =
2×1 table
EndNodes
__________
'A' 'B'
'A' 'C'
>> plot(G)
>> G = addedge(G,2,3) % 给第二个和第三个顶点之间加一条边
G =
graph - 属性:
Edges: [3×1 table]
Nodes: [3×1 table]
>> plot(G)
>> s = [1 1 1 2 2 3 3 4 5 5 6 7];
t = [2 4 8 3 7 4 6 5 6 8 7 8];
weights = [10 10 1 10 1 10 1 1 12 12 12 12]; % 加入权重
names = {'A' 'B' 'C' 'D' 'E' 'F' 'G' 'H'};
G = graph(s,t,weights,names)
G =
graph - 属性:
Edges: [12×2 table]
Nodes: [8×1 table]
>> plot(G,'EdgeLabel',G.Edges.Weight) % EdgeLabel:将权重是多少标在边上
![]()
>> % 使用邻接矩阵来创建
A = ones(4) - diag([1 1 1 1]) % 除了对角线,自己与自己相连,其余都有连线
A =
0 1 1 1
1 0 1 1
1 1 0 1
1 1 1 0
>> G = graph(A~=0)
G =
graph - 属性:
Edges: [6×1 table]
Nodes: [4×0 table]
>> figure
plot(G)
>> A = triu(magic(4))
A =
16 2 3 13
0 11 10 8
0 0 6 12
0 0 0 1
>> names = {'alpha' 'beta' 'gamma' 'delta'};
>> G = graph(A,names,'upper','OmitSelfLoops')
G =
graph - 属性:
Edges: [6×2 table]
Nodes: [4×1 table]
>> G.Edges
ans =
6×2 table
EndNodes Weight
__________________ ______
'alpha' 'beta' 2
'alpha' 'gamma' 3
'alpha' 'delta' 13
'beta' 'gamma' 10
'beta' 'delta' 8
'gamma' 'delta' 12
>> figure
>> plot(G)
>> G.Nodes
ans =
4×1 table
Name
_______
'alpha'
'beta'
'gamma'
'delta'
(2)有向图
>> s = [1 1 1 2 2 3 3 4 5 5 6 7];
t = [2 4 8 3 7 4 6 5 6 8 7 8];
weights = [10 10 1 10 1 10 1 1 12 12 12 12];
names = {'A' 'B' 'C' 'D' 'E' 'F' 'G' 'H'};
G = digraph(s,t,weights,names) % s是七点,t是终点
G =
digraph - 属性:
Edges: [12×2 table]
Nodes: [8×1 table]
>> plot(G,'Layout','force','EdgeLabel',G.Edges.Weight)
% 'Layout','force'指的是一种布局
>> plot(G,'EdgeLabel',G.Edges.Weight)
![]()
>> A = magic(4);
A(A>10) = 0
A =
0 2 3 0
5 0 10 8
9 7 6 0
4 0 0 1
>> names = {'alpha' 'beta' 'gamma' 'delta'};
>> G = digraph(A,names,'OmitSelfLoops') % 忽略环状:即自己连自己
G =
digraph - 属性:
Edges: [8×2 table]
Nodes: [4×1 table]
>> G.Edges
ans =
8×2 table
EndNodes Weight
__________________ ______
'alpha' 'beta' 2
'alpha' 'gamma' 3
'beta' 'alpha' 5
'beta' 'gamma' 10
'beta' 'delta' 8
'gamma' 'alpha' 9
'gamma' 'beta' 7
'delta' 'alpha' 4
>> G.Nodes
ans =
4×1 table
Name
_______
'alpha'
'beta'
'gamma'
'delta'
>> plot(G,'EdgeLabel',G.Edges.Weight)
>> s = [1 1 1 2 2 3];
t = [2 3 4 5 6 7];
G = digraph(s,t) %创建好有向图
G =
digraph - 属性:
Edges: [6×1 table]
Nodes: [7×0 table]
>> A = adjacency(G) %根据有向图,求邻接矩阵
A =
(1,2) 1
(1,3) 1
(1,4) 1
(2,5) 1
(2,6) 1
(3,7) 1
>> full(A) %行表示七点,列表示终点
ans =
0 1 1 1 0 0 0
0 0 0 0 1 1 0
0 0 0 0 0 0 1
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
>> s = [1 2 1 3 2 3 3 3];
t = [2 1 3 1 3 4 5 6];
G = digraph(s,t);
I = incidence(G) %稀疏矩阵
I =
(1,1) -1
(2,1) 1
(1,2) -1
(3,2) 1
(1,3) 1
(2,3) -1
(2,4) -1
(3,4) 1
(1,5) 1
(3,5) -1
(3,6) -1
(4,6) 1
(3,7) -1
(5,7) 1
(3,8) -1
(6,8) 1
>> full(I) % 全矩阵,六行八列,每一列表示一个边,-1表示起点,1表示终点
%第一行表示第一个顶点,第二行表示定二个顶点
ans =
-1 -1 1 0 1 0 0 0
1 0 -1 -1 0 0 0 0
0 1 0 1 -1 -1 -1 -1
0 0 0 0 0 1 0 0
0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 1
>> figure
>> plot(G)
![]()
2、广度优先搜索
>> s = [1 1 1 1 2 2 2 2 2 2 2 2 2 2 15 15 15 15 15];
t = [3 5 4 2 14 6 11 12 13 10 7 9 8 15 16 17 19 18 20];
G = graph(s,t);
figure
plot(G)
>> v = bfsearch(G,2) %从第2个顶点出发,进行广度优先搜索,先搜索所有与它相连的点
v =
2
1
6
7
8
9
10
11
12
13
14
15
3 %接着搜索与1相连的点
4
5
16 % 与15相连的点
17
18
19
20
% 同级别的点,是按照编号顺序来的
3、深度优先搜索
>> s = [1 1 1 1 2 2 2 2 2 2 2 2 2 2 15 15 15 15 15];
t = [3 5 4 2 14 6 11 12 13 10 7 9 8 15 16 17 19 18 20];
G = graph(s,t);
figure
plot(G)
>> v = dfsearch(G,17) % 从17开始,进行深度优先搜索,搜索距离17最近的点,
v =
17
15
2
1
3 % 找到与17相连的最长的一条线
4
5
6 % 与1相连的分支搜索完了,再搜索与2相连的分支
7
8
9
10
11
12
13
14
16 %再搜索与15相连的分支
18
19
20
4、最小生成树
>> s = [1 1 1 2 5 3 6 4 7 8 8 8];
t = [2 3 4 5 3 6 4 7 2 6 7 5];
weights = [100 10 10 10 10 20 10 30 50 10 70 10];
G = graph(s,t,weights);
figure
p = plot(G,'EdgeLabel',G.Edges.Weight);
>> T = minspantree(G);
>> T
T =
graph - 属性:
Edges: [7×2 table]
Nodes: [8×0 table]
>> highlight(p,T)
![]()
5、最短路问题
>> s = [1 1 1 1 1 2 2 7 7 9 3 3 1 4 10 8 4 5 6 8];
t = [2 3 4 5 7 6 7 5 9 6 6 10 10 10 11 11 8 8 11 9];
weights = [1 1 1 1 3 3 2 4 1 6 2 8 8 9 3 2 10 12 15 16];
G = graph(s,t,weights);
x = [0 0.5 -0.5 -0.5 0.5 0 1.5 0 2 -1.5 -2];
y = [0 0.5 0.5 -0.5 -0.5 2 0 -2 0 0 0];
figure
p = plot(G,'XData',x,'YData',y,'EdgeLabel',G.Edges.Weight);
% 并没有采用默认形式,而是指定坐标
>> [path1,d] = shortestpath(G,6,8) %第6个点到第8个点之间的最短路径
path1 =
6 3 1 4 8
d =
14
>> highlight(p,path1,'EdgeColor','g')
>> [path2,d] = shortestpath(G,6,8,'Method','unweighted') %在计算的时候不考虑权重
path2 =
6 9 8
d =
2
>> highlight(p,path2,'EdgeColor','r')
第11节 图像处理相关函数介绍
1、文件的读写
2、图像文件的读取
>> RGB = imread('football.jpg'); % 读入jpg图像文件到RGB
% 256*320个像素,3维空间,unit8格式
>> [X,map] = imread('trees.tif'); % 读入tif文件到[X,map]
% X代表颜色的索引,map对应的是颜色
3、图像显示
>> imshow(RGB)
>> imshow(X)
>> imshow(X,map)
4、图像的写入
>> imwrite(RGB,'footballtemp.jpg') % 写入jpg文件
>> imwrite(X,map,'treestemp.tif') % 写入tif文件
5、查看图像信息
info = imfinfo(filename,fmt) % 文件名,文件格式
info = imfinfo(filename)
>> info = imfinfo('canoe.tif') % canoe.tif 是系统自带的图片
info =
包含以下字段的 struct:
Filename: 'D:\MATLAB\R2018a\toolbox\images\imdata\canoe.tif'
FileModDate: '13-四月-2015 13:23:12'
FileSize: 71548
Format: 'tif'
FormatVersion: []
Width: 346
Height: 207
BitDepth: 8
ColorType: 'indexed'
FormatSignature: [73 73 42 0]
ByteOrder: 'little-endian'
NewSubFileType: 0
BitsPerSample: 8
Compression: 'PackBits'
PhotometricInterpretation: 'RGB Palette'
StripOffsets: [1×9 double]
SamplesPerPixel: 1
RowsPerStrip: 23
StripByteCounts: [7978 7919 7844 7895 7310 6796 7286 7463 7410]
XResolution: 72
YResolution: 72
ResolutionUnit: 'Inch'
Colormap: [256×3 double]
PlanarConfiguration: 'Chunky'
TileWidth: []
TileLength: []
TileOffsets: []
TileByteCounts: []
Orientation: 1
FillOrder: 1
GrayResponseUnit: 0.0100
MaxSampleValue: 255
MinSampleValue: 0
Thresholding: 1
Offset: 69708
ImageDescription: 'Copyright The MathWorks, Inc.'
>> info1 = imfinfo('treestemp.tif')
info1 =
包含以下字段的 struct:
Filename: 'E:\王萌萌\数模公司\课件\MATLAB课件\第4章 Matlab数据分析及各种算法介绍\第11节 图像处理相关函数介绍\【课件】图像处理相关函数介绍\treestemp.tif'
FileModDate: '01-九月-2021 08:53:44'
FileSize: 75764
Format: 'tif'
FormatVersion: []
Width: 350
Height: 258
BitDepth: 8
ColorType: 'indexed'
FormatSignature: [73 73 42 0]
ByteOrder: 'little-endian'
NewSubFileType: 0
BitsPerSample: 8
Compression: 'PackBits'
PhotometricInterpretation: 'RGB Palette'
StripOffsets: [1×12 double]
SamplesPerPixel: 1
RowsPerStrip: 23
StripByteCounts: [1×12 double]
XResolution: 72
YResolution: 72
ResolutionUnit: 'Inch'
Colormap: [256×3 double]
PlanarConfiguration: 'Chunky'
TileWidth: []
TileLength: []
TileOffsets: []
TileByteCounts: []
Orientation: 1
FillOrder: 1
GrayResponseUnit: 0.0100
MaxSampleValue: 255
MinSampleValue: 0
Thresholding: 1
Offset: 73930
6、图像的平移
>> I = imread('football.jpg');
se = translate(strel(1), [30 30]); % 向下和向右移动30个位置
J = imdilate(I,se); % 利用膨胀函数平移图像
subplot(121);imshow(I), title('原图')
subplot(122), imshow(J), title('移动后的图像');
>> I = imread('cameraman.tif');
figure
Flip1=fliplr(I); % 对矩阵I左右反转
subplot(131);imshow(I);title('原图');
subplot(132);imshow(Flip1);title('水平镜像');
Flip2=flipud(I); % 对矩阵I垂直反转
subplot(133);imshow(Flip2);title('竖直镜像');
7、图像缩放
>> I = imread('rice.png');
J = imresize(I, 0.5); % 缩小
figure, imshow(I), figure, imshow(J)
>> [X, map] = imread('trees.tif');
[Y, newmap] = imresize(X, map, 0.5); % 索引图像的缩小
figure, imshow(X,map)
figure, imshow(Y, newmap)
8、图像的旋转
>> I=imread('cameraman.tif');
% 双线性插值法旋转图像,并裁剪图像,使其和原图像大小一致
B=imrotate(I,60,'bilinear','crop'); % 60:旋转60度,若逆时针旋转,加个负号,bilinear:插值方法,crop:裁剪
subplot(121),imshow(I),title('原图');
subplot(122),imshow(B),title('旋转图像60^{o},并剪切图像');
9、图像的剪切
>> I = imread('circuit.tif');
I2 = imcrop(I,[75 68 130 112]); % [75 68 130 112]为剪切区域
figure
imshow(I)
figure
imshow(I2)
10、对比度增强
>> I = imread('pout.tif');
J = imadjust(I);
figure
imshow(I)
title('原始图像')
figure
imshow(J)
title('调整后图像')
>> RGB1 = imread('football.jpg');
RGB2 = imadjust(RGB1,[.2 .3 0; .6 .7 1],[]); % imadjust(I,[low_in high_in],[low_out high_out]) I,输入图像增强区域(R G B),输出
figure
imshow(RGB1)
title('原始图像')
figure
imshow(RGB2)
title('调整后图像')
11、直方图均衡化
>> I = imread('tire.tif'); % 读入系统自带的测试图片
J = histeq(I); % 使用直方图均衡化方法增强对比度
imshow(I) % 原始图像
figure, imshow(J) % 增强对比度之后的图像
figure; imhist(I,64) % 原始直方图
figure; imhist(J,64) % 增强对比度之后的直方图
12、空域滤波增强
(1)邻域平均法滤波
>> I=imread('cameraman.tif'); % cameraman.tif为系统自带的测试图片
figure
subplot(131),imshow(I);title('原图')
J=imnoise(I,'salt & pepper',0.01); % 添加椒盐噪声
subplot(132),imshow(J);title('噪声图像')
% 应用3×3邻域窗口法,fspecial函数用来实现一个均值滤波器
K1=filter2(fspecial('average',3),J,'full')/255; % 除以255来归一化
subplot(133),imshow(K1);title('3×3窗的邻域平均滤波图像')
(2)终值滤波
>> I=imread('cameraman.tif');
J=imnoise(I,'salt & pepper',0.02); % 添加椒盐噪声
figure
subplot(121),imshow(J);title('噪声图像')
K=medfilt2(J); % 使用3×3的邻域窗的中值滤波
subplot(122),imshow(K);title('中值滤波后图像')
(3)维纳滤波
>> I=imread('eight.tif');
figure
subplot(131),imshow(I);title('原图')
J=imnoise(I,'gauss',0,0.01); % 添加高斯噪声
subplot(132),imshow(J);title('噪声图像')
[K1,noise]=wiener2(J,[5 5]); % 在5×5邻域内对图像进行维纳滤波
subplot(133),imshow(K1);title('维纳滤波后图像')
第12节 金融工具箱简介
1、金钱的时间价值
现值 100 年利率5%
终值 2年后 100×1.05^2>> pv=100
r=0.05
n=2;
fv=pv*(1+r)^n
pv =
100
r =
0.0500
fv =
110.2500
>> clear
fv=100
r=0.05
n=2;
pv=fv/(1+r)^n
fv =
100
r =
0.0500
pv =
90.7029
2、内部收益率
![]()
>> Stream = [-20000, 2000, 2500, 3500, -5000, 6500, 9500, 9500, 9500];
ROR = irr(Stream)
ROR =
0.1172
% 第三年之后,可能设备老化,需要再投入5000元
% 算出来之后和银行的利率,或者其他的投资项目作对比,再考虑要不要拿去投资项目
3、房贷还款
% Payment = payper(Rate,NumPeriods,PresentValue,FutureValue,Due)
>> Payment = payper(0.056/12, 300, 1000000, 0, 0) % 此时计算的是月还款
Payment =
6.2007e+03
% 利率,多少期,现值:贷款多少,终值(还完之后,还欠银行多少钱),due:月初还是月末还款,一般都是月末
% 计算得出每个月还款6200
4、现值计算
% PresentVal = pvfix(Rate,NumPeriods,Payment,ExtraPayment,Due) 固定
>> PresentVal = pvfix(0.06/12, 5*12, 200, 0, 0)
PresentVal =
1.0345e+04
% 每个月利率,还60期,每个月还200元,还完5年之后,还需额外还0元,这笔钱折算到现在,价值10345
% PresentVal = pvvar(CashFlow,Rate) 每个月还款钱数非固定
>> PresentVal = pvvar([-10000 2000 1500 3000 3800 5000], 0.08)
PresentVal =
1.7154e+03
% 投入1000,每年挣一些钱,利率是0.08,现在可以赚多少
% 如果要计算五年后赚多少,要1715.4*1.08^5
5、终值计算
% FutureVal = fvfix(Rate,NumPeriods,Payment,PresentVal,Due) 固定
>> FutureVal = fvfix(0.09/12, 12*10, 200, 1500, 0)
FutureVal =
4.2380e+04
% 现在是1500,每个月月末挣200,放银行,再*利息,十年后,这笔钱会变成4238
% FutureVal = fvvar(CashFlow,Rate) 非固定
>> FutureVal = fvvar([-10000 2000 1500 3000 3800 5000], 0.08)
FutureVal =
2.5205e+03
% 先投入10000,每年挣这么多钱,第一年2000拿到手之后,是放进银行吃利息的,利率0.08,五年之后可以挣2520.5
第13节 神经网络算法
![]()
![]()
![]()
1、神经网络算法建模的步骤
2、神经网络工具使用演示
(1)载入测试数据
>> load simplefit_dataset
(2)进行神经网络建模、训练
1)利用matlab神经网络工具建模训练
>> nnstart % 打开 Neural Network Start GUI
>> nftool % Fitting Tool
![]()
% 就像函数一样,可以进行预测
>> net(5)
ans =
7.3192
2)使用代码建模训练
% Create a Fitting Network
hiddenLayerSize = [10 5]; % 在生成的代码中,在这里更改为数组,第一层10个神经元,第二层5个
net = fitnet(hiddenLayerSize,trainFcn);
第14节 SVM算法
>> load carsmall
>> cartable = table(Acceleration, Cylinders, Displacement,...
Horsepower, Model_Year, MPG, Weight, Origin);
% 查看怎样使用模型
>> trainedModel.HowToPredict
ans =
'To make predictions on a new table, T, use:
yfit = c.predictFcn(T)
replacing 'c' with the name of the variable that is this struct, e.g. 'trainedModel'.
The table, T, must contain the variables returned by:
c.RequiredVariables
Variable formats (e.g. matrix/vector, datatype) must match the original training data.
Additional variables are ignored.
For more information, see How to predict using an exported model.'
>> trainedModel.predictFcn(cartable(1,:)) %取出数组第一行进行预测
ans =
18
>> [trainedClassifier, validationAccuracy] = trainClassifier(cartable)
trainedClassifier =
包含以下字段的 struct:
predictFcn: @(x)svmPredictFcn(predictorExtractionFcn(x))
RequiredVariables: {1×7 cell}
ClassificationSVM: [1×1 ClassificationECOC]
About: 'This struct is a trained model exported from Classification Learner R2018a.'
HowToPredict: 'To make predictions on a new table, T, use: ↵ yfit = c.predictFcn(T) ↵replacing 'c' with the name of the variable that is this struct, e.g. 'trainedModel'. ↵ ↵The table, T, must contain the variables returned by: ↵ c.RequiredVariables ↵Variable formats (e.g. matrix/vector, datatype) must match the original training data. ↵Additional variables are ignored. ↵ ↵For more information, see How to predict using an exported model.'
validationAccuracy =
0.2447
>> trainedClassifier.predictFcn(cartable(1,:))
ans =
18
第15节 元胞自动机
1、康威生命游戏
>> life % 右击,查看文件内容
% life_modified:写了注释了
2、兰顿蚂蚁
>> LangtonsAnts
第16节 机器学习工具箱初步
1、机器学习工具箱
2、数据
>> X = magic(3);
>> X([1 5]) = [NaN NaN]
X =
NaN 1 6
3 NaN 7
4 9 2
>> var(X)
ans =
NaN NaN 7
>> nanvar(X)
ans =
0.5000 32.0000 7.0000
>> var(X,'omitnan')% 同时这种形式也可实现相同效果
ans =
0.5000 32.0000 7.0000
3、将数值类型转换为类别类型
>> load hospital % 数据类型是dataset
>> hospital=dataset2table(hospital); % 改为table数组类型
>> quantile(hospital.Age,[0,.5,1]) % 计算年龄最小值、最大值、中位数
% quantile 计算分位数
ans =
25 39 50
>> hospital.AgeCat = ordinal(hospital.Age,{'Under 30','30-39','Over 40'},...
[],[25,30,40,50]);% 间隔点,最后一类包括40及其以上年龄段
% [25,30,40,50]:指的是分类标准,25-30,30-40,大于等于40且小于50
>> getlevels(hospital.AgeCat)
ans =
1×3 ordinal 数组
Under 30 30-39 Over 40
>> hospital(2,{ 'Age' 'AgeCat'}) %提取第2行
ans =
1×2 table
Age AgeCat
___ _______
GLI-532 43 Over 40
>> p = 0:.25:1;
breaks = quantile(hospital.Weight,p); %四分位
>> breaks
breaks =
111.0000 130.5000 142.5000 180.5000 202.0000
hospital.WeightQ = ordinal(hospital.Weight,{'Q1','Q2','Q3','Q4'},...
[],breaks); %
getlevels(hospital.WeightQ)
ans =
1×4 ordinal 数组
Q1 Q2 Q3 Q4
>> hospital(2,{ 'Weight' 'WeightQ'})
ans =
1×2 table
Weight WeightQ
______ _______
GLI-532 163 Q3
>> grpstats(hospital,{'AgeCat','WeightQ'},'mean','DataVars','BloodPressure')
ans =
12×4 table
AgeCat WeightQ GroupCount mean_BloodPressure
________ _______ __________ __________________
Under 30_Q1 Under 30 Q1 6 123.17 79.667
Under 30_Q2 Under 30 Q2 3 120.33 79.667
Under 30_Q3 Under 30 Q3 2 127.5 86.5
Under 30_Q4 Under 30 Q4 4 122 78
30-39_Q1 30-39 Q1 12 121.75 81.75
30-39_Q2 30-39 Q2 9 119.56 82.556
30-39_Q3 30-39 Q3 9 121 83.222
30-39_Q4 30-39 Q4 11 125.55 87.273
Over 40_Q1 Over 40 Q1 7 122.14 84.714
Over 40_Q2 Over 40 Q2 13 123.38 79.385
Over 40_Q3 Over 40 Q3 14 123.07 84.643
Over 40_Q4 Over 40 Q4 10 124.6 85.1
>> stats = grpstats(hospital,'Sex',{'min','max'},'DataVars','Weight')
stats =
2×4 table
Sex GroupCount min_Weight max_Weight
______ __________ __________ __________
Female Female 53 111 147
Male Male 47 158 202
>> stats1 = grpstats(hospital,{'Sex','Smoker'},{'min','max'},...
'DataVars','Weight')
stats1 =
4×5 table
Sex Smoker GroupCount min_Weight max_Weight
______ ______ __________ __________ __________
Female_0 Female false 40 111 147
Female_1 Female true 13 115 146
Male_0 Male false 26 158 194
Male_1 Male true 21 164 202
4、有监督学习和无监督学习
(1)有监督学习
(2)无监督学习
(3)有监督学习的流程
Ypredicted = predict(obj,Xnew)
第17节 决策树
1、信息熵
2、条件熵
3、互信息
>> load ionosphere % Contains X and Y variables
Mdl = fitctree(X,Y) %fit:拟合,c:分类,而非回归,tree:决策树
Mdl =
ClassificationTree
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'b' 'g'}
ScoreTransform: 'none'
NumObservations: 351
Properties, Methods
>> view(Mdl)
Decision tree for classification
1 if x5<0.23154 then node 2 elseif x5>=0.23154 then node 3 else g
2 if x5<0.04144 then node 4 elseif x5>=0.04144 then node 5 else b
3 if x27<0.999945 then node 6 elseif x27>=0.999945 then node 7 else g
4 class = b
5 if x24<-0.05605 then node 8 elseif x24>=-0.05605 then node 9 else b
6 if x8<-0.89669 then node 10 elseif x8>=-0.89669 then node 11 else g
7 if x1<0.5 then node 12 elseif x1>=0.5 then node 13 else b
8 class = g
9 class = b
10 class = b
11 if x3<0.73125 then node 14 elseif x3>=0.73125 then node 15 else g
12 class = b
13 if x3<0.73004 then node 16 elseif x3>=0.73004 then node 17 else b
14 if x14<0.17103 then node 18 elseif x14>=0.17103 then node 19 else g
15 if x10<-0.755855 then node 20 elseif x10>=-0.755855 then node 21 else g
16 class = b
17 if x22<0.47714 then node 22 elseif x22>=0.47714 then node 23 else g
18 if x7<0.92561 then node 24 elseif x7>=0.92561 then node 25 else g
19 if x6<0.23199 then node 26 elseif x6>=0.23199 then node 27 else b
20 class = b
21 if x4<-0.146965 then node 28 elseif x4>=-0.146965 then node 29 else g
22 if x6<-0.727275 then node 30 elseif x6>=-0.727275 then node 31 else g
23 class = b
24 if x28<-0.23939 then node 32 elseif x28>=-0.23939 then node 33 else g
25 class = b
26 class = b
27 class = g
28 if x4<-0.15535 then node 34 elseif x4>=-0.15535 then node 35 else g
29 class = g
30 class = b
31 if x4<-0.68006 then node 36 elseif x4>=-0.68006 then node 37 else g
32 class = b
33 class = g
34 class = g
35 class = b
36 class = b
37 class = g
>> view(Mdl,'Mode','graph')
clear
load carsmall % Contains Horsepower, Weight, MPG
X = [Horsepower Weight];
Mdl = fitrtree(X,MPG) % r:回归模型
view(Mdl)
view(Mdl,'Mode','graph')
第18节 判别分析
![]()
>> clear
load fisheriris
MdlLinear = fitcdiscr(meas,species);
meanmeas = mean(meas); % 人为创建一个新的x值
meanclass = predict(MdlLinear,meanmeas) %预测
meanclass =
1×1 cell 数组
{'versicolor'}
>> % 二次
MdlQuadratic = fitcdiscr(meas,species,'DiscrimType','quadratic');
meanclass2 = predict(MdlQuadratic,meanmeas)
meanclass2 =
1×1 cell 数组
{'versicolor'}
第19节 朴素贝叶斯
1%的学生不及格
P(不及格)=0.01
不及格的学生中,男生占50%,女生占50%
P(男|不及格)=0.5
P(女|不及格)=0.5
求:一个男生不及格的概率是多少?
P(不及格|男)=?

朴素贝叶斯算法即计算各种情况的概率,然后通过以下公式进行分类预测,然后即可得到所需要的分类预测模型。>> load fisheriris
X = meas(:,1:2);
Y = species;
labels = unique(Y);
>> labels
labels =
3×1 cell 数组
{'setosa' }
{'versicolor'}
{'virginica' }
>> figure;
gscatter(X(:,1), X(:,2), species,'rgb','osd');
xlabel('Sepal length');
ylabel('Sepal width');
![]()
mdl = fitcnb(X,Y); % fit:拟合,c:分类,nb:朴素贝叶斯
% X:原始数据;Y:分类的数据
>> [xx1, xx2] = meshgrid(4:.01:8,2:.01:4.5);
XGrid = [xx1(:) xx2(:)];
>> [predictedspecies,Posterior,~] = predict(mdl,XGrid);
% predictedspecies:样本对应的类别; Posterior:三列,即三个类别,分别的概率是多少,每一行和为1
>> sz = size(xx1);
>> s = max(Posterior,[],2);
>> figure
hold on
surf(xx1,xx2,reshape(Posterior(:,1),sz),'EdgeColor','none') %第一类的概率
surf(xx1,xx2,reshape(Posterior(:,2),sz),'EdgeColor','none')
surf(xx1,xx2,reshape(Posterior(:,3),sz),'EdgeColor','none')
xlabel('Sepal length');
ylabel('Sepal width');
colorbar % 颜色条
view(2)
hold off
>> figure('Units','Normalized','Position',[0.25,0.55,0.4,0.35]);
hold on
surf(xx1,xx2,reshape(Posterior(:,1),sz),'FaceColor','red','EdgeColor','none')
surf(xx1,xx2,reshape(Posterior(:,2),sz),'FaceColor','blue','EdgeColor','none')
surf(xx1,xx2,reshape(Posterior(:,3),sz),'FaceColor','green','EdgeColor','none')
xlabel('Sepal length');
ylabel('Sepal width');
zlabel('Probability');
legend(labels)
title('Classification Probability')
alpha(0.2) % 做半透明的设置
view(3) % 设置视觉
hold off
第20节 最邻近分类
![]()
>> clear
load fisheriris
X = meas;
Y = species;
Mdl = fitcknn(X,Y,'NumNeighbors',5,'Standardize',1)% 指定查找最近的5个点,使用归一化工具
%knn:最邻近分类
Mdl =
ClassificationKNN
ResponseName: 'Y'
CategoricalPredictors: []
ClassNames: {'setosa' 'versicolor' 'virginica'}
ScoreTransform: 'none'
NumObservations: 150
Distance: 'euclidean'
NumNeighbors: 5
Properties, Methods
%得到最邻近模型
>> Mdl1 = fitcknn(X,Y,'NumNeighbors',3,...
'NSMethod','exhaustive','Distance','minkowski',...% 搜索办法:改为穷举,距离:minkowski
'Standardize',1); % 默认为kdtree,euclidean:欧氏距离
>> flwr = mean(X); % an average flower
flwrClass = predict(Mdl,flwr)
flwrClass =
1×1 cell 数组
{'versicolor'}
>> clear
load fisheriris
x = meas(:,3:4);
gscatter(x(:,1),x(:,2),species)
legend('Location','best')
>> newpoint = [5 1.45];
line(newpoint(1),newpoint(2),'marker','x','color','k',...
'markersize',10,'linewidth',2)
>> Mdl = KDTreeSearcher(x)
Mdl =
KDTreeSearcher - 属性:
BucketSize: 50
Distance: 'euclidean'
DistParameter: []
X: [150×2 double]
>> [n,d] = knnsearch(Mdl,newpoint,'k',10) % n:点的坐标编号,d:距离
n =
120 53 73 134 84 77 78 51 64 87
d =
1 至 8 列
0.0500 0.1118 0.1118 0.1118 0.1803 0.2062 0.2500 0.3041
9 至 10 列
0.3041 0.3041
>> line(x(n,1),x(n,2),'color',[.5 .5 .5],'marker','o',...
'linestyle','none','markersize',10)
>> x(n,:) % 有两组数据重复的坐标点
ans =
5.0000 1.5000
4.9000 1.5000
4.9000 1.5000
5.1000 1.5000
5.1000 1.6000
4.8000 1.4000
5.0000 1.7000
4.7000 1.4000
4.7000 1.4000
4.7000 1.5000
>> xlim([4.5 5.5]);
ylim([1 2]);
axis square
>> tabulate(species(n))
Value Count Percent
virginica 2 20.00%
versicolor 8 80.00%
>> ctr = newpoint - d(end);
diameter = 2*d(end);
% Draw a circle around the 10 nearest neighbors.
h = rectangle('position',[ctr,diameter,diameter],... %先画一个长方形,将角改为圆角
'curvature',[1 1]);
h.LineStyle = ':';
第21节 聚类分析
1、分层聚类
>> clear
load fisheriris
>> Z = linkage(meas,'average','chebychev');
>> dendrogram(Z,0) % 绘制距离计算的结果,系统树状图,0:表示绘图时显示所有分层
>> dendrogram(Z,10) % 只展示最上层的十个样本点
>> c = cluster(Z,'maxclust',3); % 分层聚类,最大分类为3个类,c的取值只有1,2,3
>> cutoff = median([Z(end-2,3) Z(end-1,3)]); % 其实就是选择一个标准,按照这个标准可以将系统树状图分为3类 median:中位数
>> dendrogram(Z,'ColorThreshold',cutoff) % 绘制聚类结果图
>> lastTwo = Z(end-1:end,:)
lastTwo =
293.0000 297.0000 1.7583
296.0000 298.0000 3.4445
>> crosstab(c,species) % 统计分类情况,c中的分类和原始数据中的分类相互对应关系
ans =
0 0 10
0 50 40
50 0 0
% 第1,2,3行:c里面的第1,2,3类;第1,2,3列:species第1,2,3类,可以看出,那个40是分错的,完美分类是对角线三个50
2、K-平均算法
clear
load fisheriris
X = meas(:,3:4);
>> figure;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
![]()
>> rng(1); % For reproducibility 设置随机种子,实际操作时不需要这一步,只是为了演示结果一样而已
[idx,C] = kmeans(X,3); % idx为分类结果,C为图中各个类别质心的坐标 用K平均算法,将结果分成三类
>> x1 = min(X(:,1)):0.01:max(X(:,1));
x2 = min(X(:,2)):0.01:max(X(:,2));
[x1G,x2G] = meshgrid(x1,x2); % 生成网格数据
XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot %将二维网格数据改成一维
>> % 指明了从哪里出发,然后只迭代一次,其实也就是按照既有质心对新的数据点进行分类
idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C);
>> figure;
gscatter(XGrid(:,1),XGrid(:,2),idx2Region,...
[0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..');
hold on;
plot(X(:,1),X(:,2),'k*','MarkerSize',5);
title 'Fisher''s Iris Data';
xlabel 'Petal Lengths (cm)';
ylabel 'Petal Widths (cm)';
legend('Region 1','Region 2','Region 3','Data','Location','SouthEast');
hold off;
3、高斯混合模型
>> clear
mu1 = [2 2]; % Mean of the 1st component
sigma1 = [2 0; 0 1]; % Covariance of the 1st component
mu2 = [-2 -1]; % Mean of the 2nd component
sigma2 = [1 0; 0 1]; % Covariance of the 2nd component
>> rng('default') % For reproducibility
r1 = mvnrnd(mu1,sigma1,1000);
r2 = mvnrnd(mu2,sigma2,1000);
X = [r1; r2];
figure
scatter(X(:,1),X(:,2),10,'.') % Scatter plot with points of size 10
hold on
>> gm = fitgmdist(X,2); % fit:拟合,gm:高斯,dist:分布 分成两类
>> ezcontour(@(x,y)pdf(gm,[x y]),[-6 8],[-4 6]) % 高斯模型概率密度分布
% ezcontour:绘制等高线 pdf:概率分布
>> idx = cluster(gm,X); % 输入数据进行聚类
>> figure;
gscatter(X(:,1),X(:,2),idx);
legend('Cluster 1','Cluster 2','Location','best');
第22节 回归分析
1、线性回归
![]()
mdl = fitlm(tbl,'ResponseVar','BloodPressure');
mdl = fitlm(X,y)
% 如果数组中某一列是类别格式,可以通过以下形式指定
mdl = fitlm(X,y,'Categorical',[2,3]);
>> clear
load carsmall
X = [Weight Horsepower Cylinders Model_Year];
y = MPG;
% 或者数组形式
>> X1 = table(Weight, Horsepower, Cylinders, Model_Year);
y1 = MPG;
(1)基本步骤
1)选择一个模型或者一组模型
mdl = fitlm(X,y,'interactions');
mdl2 = stepwiselm(tbl,'constant', ...
'Upper','linear','ResponseVar',3);
'Y ~ A + B + C' 三个变量相加,并加上常数项.
'Y ~ A + B + C - 1' 三个变量相加,并排除常数项.
'Y ~ A + B + C + B^2' 三个变量相加,并加上常数项,再加上B^2.
'Y ~ A + B^2 + C' 和上例相同,因为B的低阶项也包括进去了
'Y ~ A + B + C + A:B' 三个变量相加,并加上常数项,再加上 A*B 项.
'Y ~ A*B + C' 和上例相同, 三个变量相加,并加上常数项,再加上 A*B 项,
因为 A*B = A + B + A:B.
'Y ~ A*B*C - A:B:C' 含有ABC各项之间所有的相乘项,但是不包括三个连成项.
'Y ~ A*(B + C + D)' 含有所有的线性项,加上A和其他各变量的相乘项
mdl = fitlm(X,y,'y ~ x1*x2*x3 - x1:x2:x3');
mdl2 = stepwiselm(tbl,'y ~ 1','Upper','y ~ x1 + x2 + x3');
【A B C response】
[0 0 0 0] % Constant term or intercept
[0 1 0 0] % B; equivalently, A^0 * B^1 * C^0
[1 0 1 0] % A*C
[2 0 0 0] % A^2
[0 1 2 0] % B*(C^2)
>> clear
load hospital
dsa = table(hospital.Sex,hospital.BloodPressure(:,1), ...
hospital.Age,hospital.Smoker,'VariableNames', ...
{'Sex','BloodPressure','Age','Smoker'});
T = [0 0 0 0;1 0 0 0;0 0 1 0;0 0 0 1] % 'BloodPressure ~ 1 + Sex + Age + Smoker'
% BloodPressure:作为Y,因为这一列全是0
T =
0 0 0 0
1 0 0 0
0 0 1 0
0 0 0 1
>> dsa = table(hospital.BloodPressure(:,1),hospital.Sex, ...
hospital.Age,hospital.Smoker,'VariableNames', ...
{'BloodPressure','Sex','Age','Smoker'});
T = [0 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1] % 'BloodPressure ~ 1 + Sex + Age + Smoker'
T =
0 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
>> clear
load carsmall
X = [Acceleration,Weight];
% 'MPG ~ Acceleration + Weight + Acceleration:Weight + Weight^2'
>> T = [0 0 0;1 0 0;0 1 0;1 1 0;0 2 0]
T = % 第一列是加速,第二列是车重
0 0 0
1 0 0
0 1 0
1 1 0
0 2 0
>> mdl = fitlm(X,MPG,T) % 这里的MPG相当于Y
mdl =
Linear regression model:
y ~ 1 + x1*x2 + x2^2 % x1*x2:包括了低阶项
Estimated Coefficients:
Estimate SE tStat pValue
___________ __________ _______ __________
(Intercept) 48.906 12.589 3.8847 0.00019665 %常数项系数
x1 0.54418 0.57125 0.95261 0.34337 %x1项系数
x2 -0.012781 0.0060312 -2.1192 0.036857
x1:x2 -0.00010892 0.00017925 -0.6076 0.545
x2^2 9.7518e-07 7.5389e-07 1.2935 0.19917
% Estimate:权重, SE:误差,
Number of observations: 94, Error degrees of freedom: 89
Root Mean Squared Error: 4.1
R-squared: 0.751, Adjusted R-Squared 0.739
F-statistic vs. constant model: 67, p-value = 4.99e-26
T = [0 0 0;1 0 0;0 1 0;1 1 0];
mdl = stepwiselm(X,MPG,[0 0 0],'upper',T)
1. Adding x2, FStat = 259.3087, pValue = 1.643351e-28
mdl =
Linear regression model:
y ~ 1 + x2
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ _______ __________
(Intercept) 49.238 1.6411 30.002 2.7015e-49
x2 -0.0086119 0.0005348 -16.103 1.6434e-28
% p值远小于0.05,说明目标和变量还是非常相关的
Number of observations: 94, Error degrees of freedom: 92
Root Mean Squared Error: 4.13
R-squared: 0.738, Adjusted R-Squared 0.735
F-statistic vs. constant model: 259, p-value = 1.64e-28
2)检查效果,并调整模型
>> clear
X = randn(100,5);
y = X*[1;0;3;0;-1] + randn(100,1);
mdl = fitlm(X,y)
mdl =
Linear regression model:
y ~ 1 + x1 + x2 + x3 + x4 + x5
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ _______ __________
(Intercept) 0.080495 0.096376 0.83521 0.40571 % p值大于0.05,没什么用
x1 0.98854 0.1188 8.3212 6.735e-13
x2 0.094421 0.093578 1.009 0.31556
x3 2.9694 0.10459 28.391 6.6665e-48
x4 0.081853 0.096331 0.84971 0.39765
x5 -1.0417 0.093105 -11.188 5.6528e-19
Number of observations: 100, Error degrees of freedom: 94
Root Mean Squared Error: 0.94
R-squared: 0.907, Adjusted R-Squared 0.902
F-statistic vs. constant model: 184, p-value = 6.39e-47
>> load carsmall
tbl = table(Weight,MPG,Cylinders);
tbl.Cylinders = categorical(tbl.Cylinders); %将气缸转化为类别型
mdl = fitlm(tbl,'MPG ~ Cylinders*Weight + Weight^2');
plotDiagnostics(mdl)
>> plotDiagnostics(mdl,'cookd') % 观察异常点
![]()
>> [~,larg] = max(mdl.Diagnostics.CooksDistance);
>> larg
larg =
90 %从上图也可以看出,第90个点是异常点
>> mdl2 = fitlm(tbl,'MPG ~ Cylinders*Weight + Weight^2', ...
'Exclude',larg) %将此异常点排除,再进行训练
mdl2 =
Linear regression model:
MPG ~ 1 + Weight*Cylinders + Weight^2
Estimated Coefficients:
Estimate SE tStat pValue
___________ _________ _______ _________
(Intercept) 20.596 14.224 1.4479 0.15127
Weight 0.015482 0.011609 1.3336 0.18584
Cylinders_6 -39.926 12.734 -3.1355 0.0023481
Cylinders_8 -68.837 23.374 -2.945 0.0041536
Weight:Cylinders_6 0.012659 0.0044221 2.8628 0.0052737
Weight:Cylinders_8 0.019745 0.0072926 2.7076 0.0081745
Weight^2 -4.8505e-06 2.347e-06 -2.0667 0.041773
Number of observations: 93, Error degrees of freedom: 86
Root Mean Squared Error: 3.43
R-squared: 0.825, Adjusted R-Squared 0.813
F-statistic vs. constant model: 67.6, p-value = 1.85e-30
(2)误差图分析
>> clear
load carsmall
tbl = table(Weight,MPG,Cylinders);
tbl.Cylinders = categorical(tbl.Cylinders);
mdl = fitlm(tbl,'MPG ~ Cylinders*Weight + Weight^2')
mdl =
Linear regression model:
MPG ~ 1 + Weight*Cylinders + Weight^2
Estimated Coefficients:
Estimate SE tStat pValue
___________ __________ _______ _________
(Intercept) 16.049 15.789 1.0165 0.31222
Weight 0.019269 0.012884 1.4956 0.13839
Cylinders_6 -39.625 14.167 -2.797 0.0063494
Cylinders_8 -76.144 25.948 -2.9345 0.0042713
Weight:Cylinders_6 0.012985 0.0049194 2.6395 0.0098378
Weight:Cylinders_8 0.022039 0.0080952 2.7225 0.007828
Weight^2 -5.6217e-06 2.6048e-06 -2.1582 0.033668
Number of observations: 94, Error degrees of freedom: 87
Root Mean Squared Error: 3.82
R-squared: 0.789, Adjusted R-Squared 0.774
F-statistic vs. constant model: 54.1, p-value = 2.82e-27
>> plotResiduals(mdl)
>> plotResiduals(mdl,'probability')
![]()
>> outl = find(mdl.Residuals.Raw > 12)
outl =
90
97
% 从上图也可以看出,第90和97个点误差较大
>> mdl2 = fitlm(tbl,'MPG ~ Cylinders*Weight + Weight^2', ...
'Exclude',outl); % 剔除90和97个点,重新建模
>> plotResiduals(mdl2)
(3)考察变量的影响
>> load carsmall
tbl = table(Weight,MPG,Cylinders);
tbl.Cylinders = categorical(tbl.Cylinders);
mdl = fitlm(tbl,'MPG ~ Cylinders*Weight + Weight^2');
plotSlice(mdl)
>> plotInteraction(mdl,'Cylinders','Weight','predictions')
>> plotInteraction(mdl,'Weight','Cylinders','predictions')
(4)改变模型
>> clear
load carbig
tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG);
mdl = fitlm(tbl,'linear','ResponseVar','MPG')
mdl =
Linear regression model:
MPG ~ 1 + Acceleration + Displacement + Horsepower + Weight
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ ________ __________
(Intercept) 45.251 2.456 18.424 7.0721e-55
Acceleration -0.023148 0.1256 -0.1843 0.85388
Displacement -0.0060009 0.0067093 -0.89441 0.37166
Horsepower -0.043608 0.016573 -2.6312 0.008849
Weight -0.0052805 0.00081085 -6.5123 2.3025e-10
Number of observations: 392, Error degrees of freedom: 387
Root Mean Squared Error: 4.25
R-squared: 0.707, Adjusted R-Squared 0.704
F-statistic vs. constant model: 233, p-value = 9.63e-102
% 从最初的初始值开始一步一步训练
>> mdl1 = step(mdl,'NSteps',10) % 使用step函数改进模型
1. Adding Displacement:Horsepower, FStat = 87.4802, pValue = 7.05273e-19
mdl1 =
Linear regression model:
MPG ~ 1 + Acceleration + Weight + Displacement*Horsepower
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ _______ __________
(Intercept) 61.285 2.8052 21.847 1.8593e-69
Acceleration -0.34401 0.11862 -2.9 0.0039445
Displacement -0.081198 0.010071 -8.0623 9.5014e-15
Horsepower -0.24313 0.026068 -9.3265 8.6556e-19
Weight -0.0014367 0.00084041 -1.7095 0.088166
Displacement:Horsepower 0.00054236 5.7987e-05 9.3531 7.0527e-19
Number of observations: 392, Error degrees of freedom: 386
Root Mean Squared Error: 3.84
R-squared: 0.761, Adjusted R-Squared 0.758
F-statistic vs. constant model: 246, p-value = 1.32e-117
>> mdl2 = removeTerms(mdl1,'Acceleration + Weight') 去掉mdl1中某些项
mdl2 =
Linear regression model:
MPG ~ 1 + Displacement*Horsepower
Estimated Coefficients:
Estimate SE tStat pValue
__________ _________ _______ ___________
(Intercept) 53.051 1.526 34.765 3.0201e-121
Displacement -0.098046 0.0066817 -14.674 4.3203e-39
Horsepower -0.23434 0.019593 -11.96 2.8024e-28
Displacement:Horsepower 0.00058278 5.193e-05 11.222 1.6816e-25
Number of observations: 392, Error degrees of freedom: 388
Root Mean Squared Error: 3.94
R-squared: 0.747, Adjusted R-Squared 0.745
F-statistic vs. constant model: 381, p-value = 3e-115
(5)使用模型进行预测
1)predict
>> clear
load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
mdl = fitlm(X,MPG);
Xnew = [nanmin(X);nanmean(X);nanmax(X)]; % new data
>> Xnew
Xnew =
1.0e+03 *
0.0080 0.0680 0.0460 1.6130
0.0155 0.1948 0.1051 2.9794
0.0248 0.4550 0.2300 5.1400
>> [NewMPG, NewMPGCI] = predict(mdl,Xnew)
NewMPG =
34.1345
23.4078
4.7751
NewMPGCI = %置信区间
31.6115 36.6575
22.9859 23.8298
0.6134 8.9367
2)feval
>> load carbig
tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG);
mdl = fitlm(tbl,'linear','ResponseVar','MPG');
X = [Acceleration,Displacement,Horsepower,Weight];
Xnew = [nanmin(X);nanmean(X);nanmax(X)]; % new data
NewMPG = feval(mdl,Xnew)
NewMPG =
34.1345
23.4078
4.7751
3)random
>> load carbig
X = [Acceleration,Displacement,Horsepower,Weight];
mdl = fitlm(X,MPG);
Xnew = [nanmin(X);nanmean(X);nanmax(X)]; % new data
rng('default') % for reproducibility
NewMPG1 = random(mdl,Xnew) % 可以多次运行,查看趋势,比如第三个解是相当不稳定的,说明模型不太靠谱
NewMPG1 =
36.4178
31.1958
-4.8176
>> NewMPG2 = random(mdl,Xnew)
NewMPG2 =
37.7959
24.7615
-0.7783
>> NewMPG3 = random(mdl,Xnew)
NewMPG3 =
32.2931
24.8628
19.9715
(6)分享保存模型
>> clear
>> load carbig
tbl = table(Acceleration,Displacement,Horsepower,Weight,MPG);
mdl = fitlm(tbl,'linear','ResponseVar','MPG');
>> mdl
mdl =
Linear regression model:
MPG ~ 1 + Acceleration + Displacement + Horsepower + Weight
Estimated Coefficients:
Estimate SE tStat pValue
__________ __________ ________ __________
(Intercept) 45.251 2.456 18.424 7.0721e-55
Acceleration -0.023148 0.1256 -0.1843 0.85388
Displacement -0.0060009 0.0067093 -0.89441 0.37166
Horsepower -0.043608 0.016573 -2.6312 0.008849
Weight -0.0052805 0.00081085 -6.5123 2.3025e-10
Number of observations: 392, Error degrees of freedom: 387
Root Mean Squared Error: 4.25
R-squared: 0.707, Adjusted R-Squared 0.704
F-statistic vs. constant model: 233, p-value = 9.63e-102
>> mdl.CoefficientNames
mdl.Coefficients.Estimate
mdl.Formula
ans =
1×5 cell 数组
1 至 4 列
{'(Intercept)'} {'Acceleration'} {'Displacement'} {'Horsepower'}
5 列
{'Weight'}
ans =
45.2511
-0.0231
-0.0060
-0.0436
-0.0053
ans =
MPG ~ 1 + Acceleration + Displacement + Horsepower + Weight
(7)类别数组的回归
>> load carsmall
figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
title('MPG vs. Weight, Grouped by Model Year')
>> cars = table(MPG,Weight,Model_Year);
cars.Model_Year = categorical(cars.Model_Year);
fit = fitlm(cars,'MPG~Weight*Model_Year')
fit =
Linear regression model:
MPG ~ 1 + Weight*Model_Year
Estimated Coefficients:
Estimate SE tStat pValue
___________ __________ ________ __________
(Intercept) 37.399 2.1466 17.423 2.8607e-30
Weight -0.0058437 0.00061765 -9.4612 4.6077e-15
% 默认按照70年
Model_Year_76 4.6903 2.8538 1.6435 0.10384
Model_Year_82 21.051 4.157 5.0641 2.2364e-06
Weight:Model_Year_76 -0.00082009 0.00085468 -0.95953 0.33992
Weight:Model_Year_82 -0.0050551 0.0015636 -3.2329 0.0017256
Number of observations: 94, Error degrees of freedom: 88
Root Mean Squared Error: 2.79
R-squared: 0.886, Adjusted R-Squared 0.88
F-statistic vs. constant model: 137, p-value = 5.79e-40
![]()
>> w = linspace(min(Weight),max(Weight));
figure()
gscatter(Weight,MPG,Model_Year,'bgr','x.o')
line(w,feval(fit,w,'70'),'Color','b','LineWidth',2)
line(w,feval(fit,w,'76'),'Color','g','LineWidth',2)
line(w,feval(fit,w,'82'),'Color','r','LineWidth',2)
title('Fitted Regression Lines by Model Year')
(8)稳定回归
>> load moore
X = [moore(:,1:5)];
y = moore(:,6);
mdl = fitlm(X,y); % not robust
mdlr = fitlm(X,y,'RobustOpts','on'); % 打开稳定回归
>> subplot(1,2,1)
plotResiduals(mdl,'probability')
subplot(1,2,2)
plotResiduals(mdlr,'probability')
>> [~,outlier] = max(mdlr.Residuals.Raw);
mdlr.Robust.Weights(outlier)
ans =
0.0246
>> median(mdlr.Robust.Weights)
ans =
0.9718
2、非线性回归
>> clear
load reaction
xn % x名称
yn % y名称
beta0 = ones(5,1); %初始值
mdl = fitnlm(reactants,...
rate,@hougen,beta0) %beta0:起始值
xn =
3×10 char 数组
'Hydrogen '
'n-Pentane '
'Isopentane'
yn =
'Reaction Rate'
mdl =
Nonlinear regression model:
y ~ hougen(b,X)
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ _______
b1 1.2526 0.86702 1.4447 0.18654
b2 0.062776 0.043562 1.4411 0.18753
b3 0.040048 0.030885 1.2967 0.23089
b4 0.11242 0.075158 1.4957 0.17309
b5 1.1914 0.83671 1.4239 0.1923
Number of observations: 13, Error degrees of freedom: 8
Root Mean Squared Error: 0.193
R-Squared: 0.999, Adjusted R-Squared 0.998
F-statistic vs. zero model: 3.91e+03, p-value = 2.54e-13
>> plotResiduals(mdl)
>> plotDiagnostics(mdl,'cookd')
>> mdl1 = fitnlm(reactants,...
rate,@hougen,ones(5,1),'Exclude',6)
mdl1 =
Nonlinear regression model:
y ~ hougen(b,X)
Estimated Coefficients:
Estimate SE tStat pValue
________ ________ ______ _______
b1 0.619 0.4552 1.3598 0.21605
b2 0.030377 0.023061 1.3172 0.22924
b3 0.018927 0.01574 1.2024 0.26828
b4 0.053411 0.041084 1.3 0.23476
b5 2.4125 1.7903 1.3475 0.2198
Number of observations: 12, Error degrees of freedom: 7
Root Mean Squared Error: 0.198
R-Squared: 0.999, Adjusted R-Squared 0.998
F-statistic vs. zero model: 2.67e+03, p-value = 2.54e-11
>> Xnew = [200,200,200;100,200,100;500,50,5];
[ypred, yci] = predict(mdl,Xnew)
ypred =
1.8762
6.2793
1.6718
yci =
1.6283 2.1242
5.9789 6.5797
1.5589 1.7846
>> [ypred1, yci1] = predict(mdl1,Xnew)
ypred1 =
1.8984
6.2555
1.6594
yci1 =
1.6260 2.1708
5.9323 6.5787
1.5345 1.7843
3、SVM回归
>> load carsmall
rng 'default' % For reproducibility
X = [Horsepower,Weight];
Y = MPG;
Mdl = fitrsvm(X,Y) %r:回归
Mdl =
RegressionSVM
ResponseName: 'Y'
CategoricalPredictors: []
ResponseTransform: 'none'
Alpha: [75×1 double]
Bias: 43.2943
KernelParameters: [1×1 struct]
NumObservations: 93
BoxConstraints: [93×1 double]
ConvergenceInfo: [1×1 struct]
IsSupportVector: [93×1 logical]
Solver: 'SMO'
Properties, Methods
4、回归树
>> load carsmall;
tree = fitrtree([Weight, Cylinders],MPG,...
'categoricalpredictors',2,'MinParentSize',20,...
'PredictorNames',{'W','C'})
% MinParentSize 最小的父节点样本个数 categoricalpredictors:类别数组
tree =
RegressionTree
PredictorNames: {'W' 'C'}
ResponseName: 'Y'
CategoricalPredictors: 2
ResponseTransform: 'none'
NumObservations: 94
Properties, Methods
>> mileage4K = predict(tree,[4000 4; 4000 6; 4000 8])
mileage4K =
19.2778
19.2778
14.3889
第23节 App Designer
1、App Desinger的主要特点
2、设计界面的内容
>> appdesigner
第24节 特征选择
1、邻里成分分析
2、fscnca函数
>> rng(0,'twister'); % For reproducibility
N = 100;
X = rand(N,20);
y = -ones(N,1);
y(X(:,3).*X(:,9)./X(:,15) < 0.4) = 1;
>> mdl = fscnca(X,y,'Solver','sgd','Verbose',1);
% x:一百行二十列 每行是一个样本,每列是一个变量 solver:求解器
% 训练出模型mdl
o Tuning initial learning rate: NumTuningIterations = 20, TuningSubsetSize = 100
|===============================================|
| TUNING | TUNING SUBSET | LEARNING |
| ITER | FUN VALUE | RATE |
|===============================================|
| 1 | -3.755936e-01 | 2.000000e-01 |
| 2 | -3.950971e-01 | 4.000000e-01 |
| 3 | -4.311848e-01 | 8.000000e-01 |
| 4 | -4.903195e-01 | 1.600000e+00 |
| 5 | -5.630190e-01 | 3.200000e+00 |
| 6 | -6.166993e-01 | 6.400000e+00 |
| 7 | -6.255669e-01 | 1.280000e+01 |
| 8 | -6.255669e-01 | 1.280000e+01 |
| 9 | -6.255669e-01 | 1.280000e+01 |
| 10 | -6.255669e-01 | 1.280000e+01 |
| 11 | -6.255669e-01 | 1.280000e+01 |
| 12 | -6.255669e-01 | 1.280000e+01 |
| 13 | -6.255669e-01 | 1.280000e+01 |
| 14 | -6.279210e-01 | 2.560000e+01 |
| 15 | -6.279210e-01 | 2.560000e+01 |
| 16 | -6.279210e-01 | 2.560000e+01 |
| 17 | -6.279210e-01 | 2.560000e+01 |
| 18 | -6.279210e-01 | 2.560000e+01 |
| 19 | -6.279210e-01 | 2.560000e+01 |
| 20 | -6.279210e-01 | 2.560000e+01 |
o Solver = SGD, MiniBatchSize = 10, PassLimit = 5
|==========================================================================================|
| PASS | ITER | AVG MINIBATCH | AVG MINIBATCH | NORM STEP | LEARNING |
| | | FUN VALUE | NORM GRAD | | RATE |
|==========================================================================================|
| 0 | 9 | -5.658450e-01 | 4.492407e-02 | 9.290605e-01 | 2.560000e+01 |
| 1 | 19 | -6.131382e-01 | 4.923625e-02 | 7.421541e-01 | 1.280000e+01 |
| 2 | 29 | -6.225056e-01 | 3.738784e-02 | 3.277588e-01 | 8.533333e+00 |
| 3 | 39 | -6.233366e-01 | 4.947901e-02 | 5.431133e-01 | 6.400000e+00 |
| 4 | 49 | -6.238576e-01 | 3.445763e-02 | 2.946188e-01 | 5.120000e+00 |
Two norm of the final step = 2.946e-01
Relative two norm of the final step = 6.588e-02, TolX = 1.000e-06
EXIT: Iteration or pass limit reached.
>> figure()
plot(mdl.FeatureWeights,'ro')
grid on
xlabel('Feature index')
ylabel('Feature weight')
3、fscnca函数调节正则化参数
clear
load('twodimclassdata.mat');
figure()
gscatter(X(:,1),X(:,2),y)
xlabel('x1')
ylabel('x2')
>> n = size(X,1);
rng('default')
XwithBadFeatures = [X,randn(n,100)*sqrt(20)];
XwithBadFeatures=(XwithBadFeatures-min(XwithBadFeatures))./range(XwithBadFeatures,1);
X = XwithBadFeatures;
>> ncaMdl = fscnca(X,y,'FitMethod','exact','Verbose',1,...
'Solver','lbfgs');
% 'FitMethod','exact' 使用所有的数据进行拟合
% 'Verbose',1 信息显示
% 'Solver','lbfgs' 求解器的设置,'lbfgs' — Limited memory Broyden-Fletcher-Goldfarb-Shanno (LBFGS) algorithm
o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 0 | 9.519258e-03 | 1.494e-02 | 0.000e+00 | | 4.015e+01 | 0.000e+00 | YES |
| 1 | -3.093574e-01 | 7.186e-03 | 4.018e+00 | OK | 8.956e+01 | 1.000e+00 | YES |
| 2 | -4.809455e-01 | 4.444e-03 | 7.123e+00 | OK | 9.943e+01 | 1.000e+00 | YES |
| 3 | -4.938877e-01 | 3.544e-03 | 1.464e+00 | OK | 9.366e+01 | 1.000e+00 | YES |
| 4 | -4.964759e-01 | 2.901e-03 | 6.084e-01 | OK | 1.554e+02 | 1.000e+00 | YES |
| 5 | -4.972077e-01 | 1.323e-03 | 6.129e-01 | OK | 1.195e+02 | 5.000e-01 | YES |
| 6 | -4.974743e-01 | 1.569e-04 | 2.155e-01 | OK | 1.003e+02 | 1.000e+00 | YES |
| 7 | -4.974868e-01 | 3.844e-05 | 4.161e-02 | OK | 9.835e+01 | 1.000e+00 | YES |
| 8 | -4.974874e-01 | 1.417e-05 | 1.073e-02 | OK | 1.043e+02 | 1.000e+00 | YES |
| 9 | -4.974874e-01 | 4.893e-06 | 1.781e-03 | OK | 1.530e+02 | 1.000e+00 | YES |
| 10 | -4.974874e-01 | 9.404e-08 | 8.947e-04 | OK | 1.670e+02 | 1.000e+00 | YES |
Infinity norm of the final gradient = 9.404e-08
Two norm of the final step = 8.947e-04, TolX = 1.000e-06
Relative infinity norm of the final gradient = 9.404e-08, TolFun = 1.000e-06
EXIT: Local minimum found.
>> figure
semilogx(ncaMdl.FeatureWeights,'ro');
xlabel('Feature index');
ylabel('Feature weight');
grid on;
figure % 和上面的图作对比
plot(ncaMdl.FeatureWeights,'ro');
xlabel('Feature index');
ylabel('Feature weight');
grid on;
>> % 对于每一折来说cvpartition将 4/5的数据作为训练集,另外1/5作为测试集
cvp = cvpartition(y,'kfold',5);
numtestsets = cvp.NumTestSets;
lambdavalues = linspace(0,2,20)/length(y);
>> lossvalues = zeros(length(lambdavalues),numtestsets);
for i = 1:length(lambdavalues) % 对lambda的数值进行循环
for k = 1:numtestsets % 对测试集进行循环
% 提取训练集
Xtrain = X(cvp.training(k),:);
ytrain = y(cvp.training(k),:);
% 提取测试集
Xtest = X(cvp.test(k),:);
ytest = y(cvp.test(k),:);
% 使用训练集训练nca模型
ncaMdl = fscnca(Xtrain,ytrain,'FitMethod','exact',...
'Solver','lbfgs','Lambda',lambdavalues(i));
% 使用nca模型对测试集的损失函数进行计算。
lossvalues(i,k) = loss(ncaMdl,Xtest,ytest,...
'LossFunction','quadratic');
end
end
>> figure()
plot(lambdavalues,mean(lossvalues,2),'ro-');
xlabel('Lambda values');
ylabel('Loss values');
grid on;
>> [~,idx] = min(mean(lossvalues,2)); % Find the index
bestlambda = lambdavalues(idx) % Find the best lambda value
bestlambda =
0.0037
>> ncaMdl = fscnca(X,y,'FitMethod','exact','Verbose',1,...
'Solver','lbfgs','Lambda',bestlambda);
o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 0 | -1.246913e-01 | 1.231e-02 | 0.000e+00 | | 4.873e+01 | 0.000e+00 | YES |
| 1 | -3.411330e-01 | 5.717e-03 | 3.618e+00 | OK | 1.068e+02 | 1.000e+00 | YES |
| 2 | -5.226111e-01 | 3.763e-02 | 8.252e+00 | OK | 7.825e+01 | 1.000e+00 | YES |
| 3 | -5.817731e-01 | 8.496e-03 | 2.340e+00 | OK | 5.591e+01 | 5.000e-01 | YES |
| 4 | -6.132632e-01 | 6.863e-03 | 2.526e+00 | OK | 8.228e+01 | 1.000e+00 | YES |
| 5 | -6.135264e-01 | 9.373e-03 | 7.341e-01 | OK | 3.244e+01 | 1.000e+00 | YES |
| 6 | -6.147894e-01 | 1.182e-03 | 2.933e-01 | OK | 2.447e+01 | 1.000e+00 | YES |
| 7 | -6.148714e-01 | 6.392e-04 | 6.688e-02 | OK | 3.195e+01 | 1.000e+00 | YES |
| 8 | -6.149524e-01 | 6.521e-04 | 9.934e-02 | OK | 1.236e+02 | 1.000e+00 | YES |
| 9 | -6.149972e-01 | 1.154e-04 | 1.191e-01 | OK | 1.171e+02 | 1.000e+00 | YES |
| 10 | -6.149990e-01 | 2.922e-05 | 1.983e-02 | OK | 7.365e+01 | 1.000e+00 | YES |
| 11 | -6.149993e-01 | 1.556e-05 | 8.354e-03 | OK | 1.288e+02 | 1.000e+00 | YES |
| 12 | -6.149994e-01 | 1.147e-05 | 7.256e-03 | OK | 2.332e+02 | 1.000e+00 | YES |
| 13 | -6.149995e-01 | 1.040e-05 | 6.781e-03 | OK | 2.287e+02 | 1.000e+00 | YES |
| 14 | -6.149996e-01 | 9.015e-06 | 6.265e-03 | OK | 9.974e+01 | 1.000e+00 | YES |
| 15 | -6.149996e-01 | 7.763e-06 | 5.206e-03 | OK | 2.919e+02 | 1.000e+00 | YES |
| 16 | -6.149997e-01 | 8.374e-06 | 1.679e-02 | OK | 6.878e+02 | 1.000e+00 | YES |
| 17 | -6.149997e-01 | 9.387e-06 | 9.542e-03 | OK | 1.284e+02 | 5.000e-01 | YES |
| 18 | -6.149997e-01 | 3.250e-06 | 5.114e-03 | OK | 1.225e+02 | 1.000e+00 | YES |
| 19 | -6.149997e-01 | 1.574e-06 | 1.275e-03 | OK | 1.808e+02 | 1.000e+00 | YES |
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 20 | -6.149997e-01 | 5.764e-07 | 6.765e-04 | OK | 2.905e+02 | 1.000e+00 | YES |
Infinity norm of the final gradient = 5.764e-07
Two norm of the final step = 6.765e-04, TolX = 1.000e-06
Relative infinity norm of the final gradient = 5.764e-07, TolFun = 1.000e-06
EXIT: Local minimum found.
>> figure
semilogx(ncaMdl.FeatureWeights,'ro');
xlabel('Feature index');
ylabel('Feature weight');
grid on;
4、fsrnca函数
>> rng(0,'twister'); % For reproducibility
N = 100;
X = rand(N,20);
y = 1 + X(:,3)*5 + sin(X(:,9)./X(:,15) + 0.25*randn(N,1));
mdl = fsrnca(X,y,'Verbose',1,'Lambda',0.5/N);
o Solver = LBFGS, HessianHistorySize = 15, LineSearchMethod = weakwolfe
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 0 | 1.636932e+00 | 3.688e-01 | 0.000e+00 | | 1.627e+00 | 0.000e+00 | YES |
| 1 | 8.304833e-01 | 1.083e-01 | 2.449e+00 | OK | 9.194e+00 | 4.000e+00 | YES |
| 2 | 7.548105e-01 | 1.341e-02 | 1.164e+00 | OK | 1.095e+01 | 1.000e+00 | YES |
| 3 | 7.346997e-01 | 9.752e-03 | 6.383e-01 | OK | 2.979e+01 | 1.000e+00 | YES |
| 4 | 7.053407e-01 | 1.605e-02 | 1.712e+00 | OK | 5.809e+01 | 1.000e+00 | YES |
| 5 | 6.970502e-01 | 9.106e-03 | 8.818e-01 | OK | 6.223e+01 | 1.000e+00 | YES |
| 6 | 6.952347e-01 | 5.522e-03 | 6.382e-01 | OK | 3.280e+01 | 1.000e+00 | YES |
| 7 | 6.946302e-01 | 9.102e-04 | 1.952e-01 | OK | 3.380e+01 | 1.000e+00 | YES |
| 8 | 6.945037e-01 | 6.557e-04 | 9.942e-02 | OK | 8.490e+01 | 1.000e+00 | YES |
| 9 | 6.943908e-01 | 1.997e-04 | 1.756e-01 | OK | 1.124e+02 | 1.000e+00 | YES |
| 10 | 6.943785e-01 | 3.478e-04 | 7.755e-02 | OK | 7.621e+01 | 1.000e+00 | YES |
| 11 | 6.943728e-01 | 1.428e-04 | 3.416e-02 | OK | 3.649e+01 | 1.000e+00 | YES |
| 12 | 6.943711e-01 | 1.128e-04 | 1.231e-02 | OK | 6.092e+01 | 1.000e+00 | YES |
| 13 | 6.943688e-01 | 1.066e-04 | 2.326e-02 | OK | 9.319e+01 | 1.000e+00 | YES |
| 14 | 6.943655e-01 | 9.324e-05 | 4.399e-02 | OK | 1.810e+02 | 1.000e+00 | YES |
| 15 | 6.943603e-01 | 1.206e-04 | 8.823e-02 | OK | 4.609e+02 | 1.000e+00 | YES |
| 16 | 6.943582e-01 | 1.701e-04 | 6.669e-02 | OK | 8.425e+01 | 5.000e-01 | YES |
| 17 | 6.943552e-01 | 5.160e-05 | 6.473e-02 | OK | 8.832e+01 | 1.000e+00 | YES |
| 18 | 6.943546e-01 | 2.477e-05 | 1.215e-02 | OK | 7.925e+01 | 1.000e+00 | YES |
| 19 | 6.943546e-01 | 1.077e-05 | 6.086e-03 | OK | 1.378e+02 | 1.000e+00 | YES |
|====================================================================================================|
| ITER | FUN VALUE | NORM GRAD | NORM STEP | CURV | GAMMA | ALPHA | ACCEPT |
|====================================================================================================|
| 20 | 6.943545e-01 | 2.260e-05 | 4.071e-03 | OK | 5.856e+01 | 1.000e+00 | YES |
| 21 | 6.943545e-01 | 4.250e-06 | 1.109e-03 | OK | 2.964e+01 | 1.000e+00 | YES |
| 22 | 6.943545e-01 | 1.916e-06 | 8.356e-04 | OK | 8.649e+01 | 1.000e+00 | YES |
| 23 | 6.943545e-01 | 1.083e-06 | 5.270e-04 | OK | 1.168e+02 | 1.000e+00 | YES |
| 24 | 6.943545e-01 | 1.791e-06 | 2.673e-04 | OK | 4.016e+01 | 1.000e+00 | YES |
| 25 | 6.943545e-01 | 2.596e-07 | 1.111e-04 | OK | 3.154e+01 | 1.000e+00 | YES |
Infinity norm of the final gradient = 2.596e-07
Two norm of the final step = 1.111e-04, TolX = 1.000e-06
Relative infinity norm of the final gradient = 2.596e-07, TolFun = 1.000e-06
EXIT: Local minimum found.
>> figure()
plot(mdl.FeatureWeights,'ro')
grid on
xlabel('Feature index')
ylabel('Feature weight')
![]()