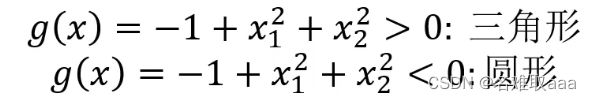机器学习之逻辑回归：芯片质量预测

---

前言

在上一篇文章中用逻辑回归方法解决了一个考试预测问题，这次我们依然用逻辑回归方法来解决一个芯片质量预测问题，但本次实战和上一次有所不同，本次实战中运用了以函数的方式求解边界曲线并且描绘出完整的决策边界曲线

---

邏輯回歸的概念

logistic回归是一种广义线性回归（generalized linear model），因此与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w‘x+b作为因变量，即y =w‘x+b，而logistic回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。

logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归

Logistic回归模型的适用条件：

1. 因变量为二分类的分类变量或某事件的发生率，并且是数值型变量。但是需要注意，重复计数现象指标不适用于Logistic回归。

2. 残差和因变量都要服从二项分布。二项分布对应的是分类变量，所以不是正态分布，进而不是用最小二乘法，而是最大似然法来解决方程估计和检验问题。

3. 自变量和Logistic概率是线性关系

4. 各观测对象间相互独立。

原理：如果直接将线性回归的模型扣到Logistic回归中，会造成方程二边取值区间不同和普遍的非直线关系。因为Logistic中因变量为二分类变量，某个概率作为方程的因变量估计值取值范围为0-1，但是，方程右边取值范围是无穷大或者无穷小。所以，才引入Logistic回归。

Logistic回归实质：发生概率除以没有发生概率再取对数。就是这个不太繁琐的变换改变了取值区间的矛盾和因变量自变量间的曲线关系。究其原因，是发生和未发生的概率成为了比值 ，这个比值就是一个缓冲，将取值范围扩大，再进行对数变换，整个因变量改变。不仅如此，这种变换往往使得因变量和自变量之间呈线性关系，这是根据大量实践而总结。所以，Logistic回归从根本上解决因变量要不是连续变量怎么办的问题。还有，Logistic应用广泛的原因是许多现实问题跟它的模型吻合。例如一件事情是否发生跟其他数值型自变量的关系。

---

逻辑回归方程

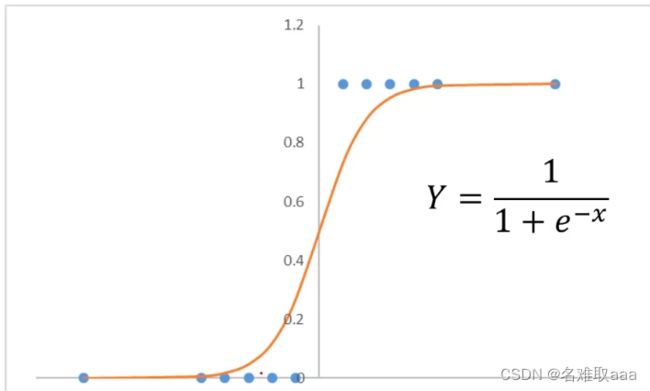
可以发现当样本值越大y越接近1，样本值越小y越接近0，以0.5为分界点就可以将y分成以下两种情况。

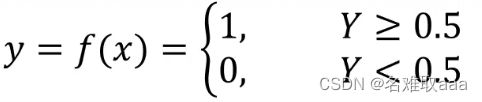
这时负样本就是0，正样本就是1，0和1就是我们给样本定义的标签。在考试通过问题中，可以用1代表通过（pass）,用0代表失败（failed），这样就可以通过标签0和1将失败和通过进行一个分类，就可以很好地解决二分类问题了。

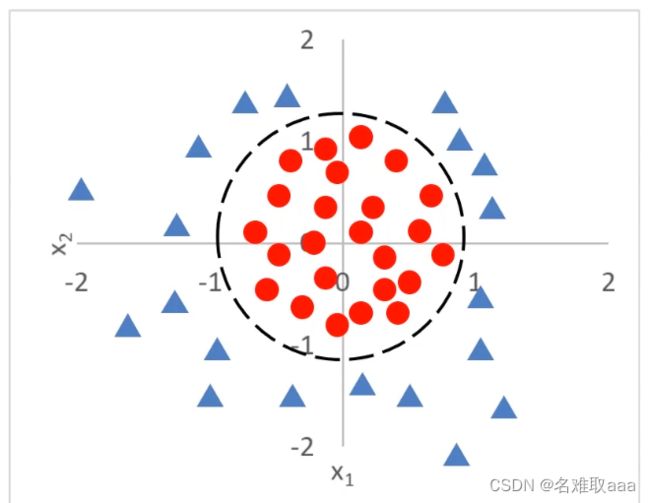
当问题更复杂时，可以用g(x)代替x，然后就可以根据g(x)寻找最合适的决策边界从而解决二分类问题

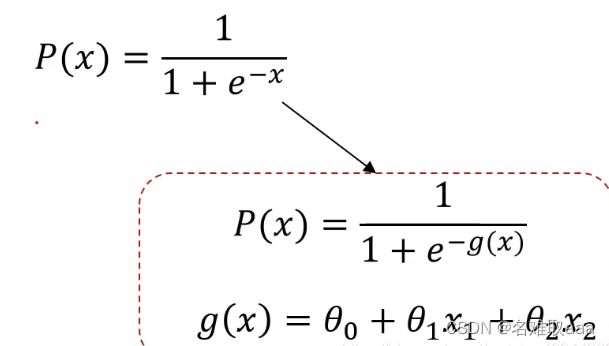
比如下面这个图形：

此时虚线部分就是它的决策边界

實戰

大部分跟上一篇的一樣就直接拷貝過來了

#load the data
import pandas as pd
import numpy as np
data = pd.read_csv('chip_test.csv')
data.head()

#visualize the data
from matplotlib import pyplot as plt
fig1 = plt.figure()
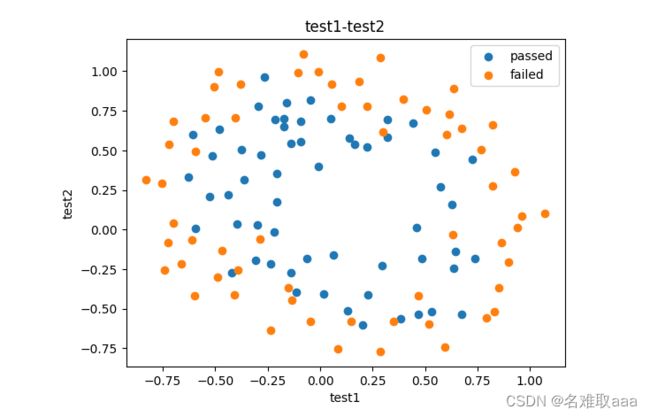
plt.scatter(data.loc[:,'test1'],data.loc[:,'test2'])
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.show()

#add label mask
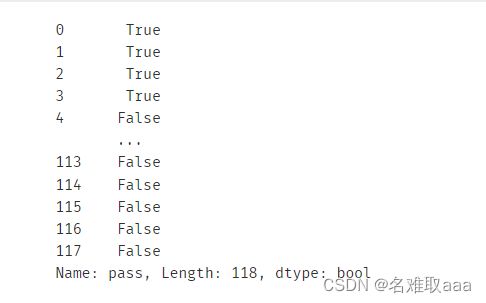
mask=data.loc[:,'pass']==1
print(mask)

fig2 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()

#define X,y
X = data.drop(['pass'],axis=1)
y = data.loc[:,'pass']
X1 = data.loc[:,'test1']
X2 = data.loc[:,'test2']
X1.head()

# create new data
X1_2 = X1*X1
X2_2 = X2*X2
X1_X2 = X1*X2
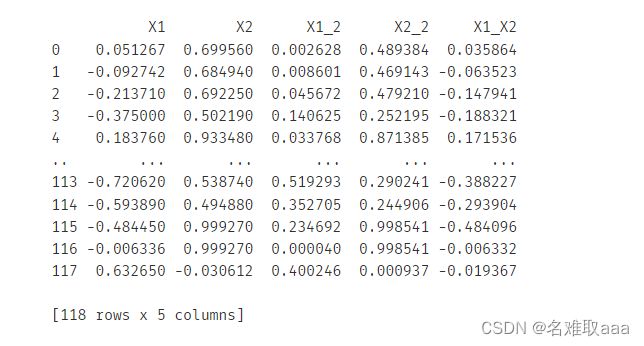
X_new = {'X1':X1,'X2':X2,'X1_2':X1_2,'X2_2':X2_2,'X1_X2':X1_X2}#将所有数据放到一个字典里面
X_new = pd.DataFrame(X_new) #方便后面进行模型数据的加载
print(X_new)

#establish new model and train
from sklearn.linear_model import LogisticRegression
LR1 = LogisticRegression()
LR1.fit(X_new,y)

這樣就訓練好模型了

#show the predicted result and its accuracy
from sklearn.metrics import accuracy_score
y1_predict = LR1.predict(X_new)
accuracy1 = accuracy_score(y,y1_predict)
print(accuracy1)

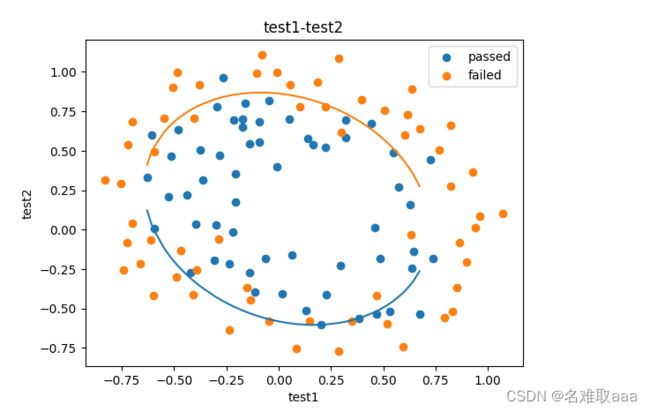
從accuracy分數0.8可以看出還行吧，畢竟有些點混在裏面和外面了，二階也難以分開得試試更高階吧

X1_new = X1.sort_values()
theta0 = LR1.intercept_
theta1,theta2,theta3,theta4,theta5 = LR1.coef_[0][0],LR1.coef_[0][1],LR1.coef_[0][2],LR1.coef_[0][3],LR1.coef_[0][4]
a = theta4
b = theta5*X1_new+theta2
c = theta0+theta1*X1_new+theta3*X1_new*X1_new
X2_new_boundary = (-b+np.sqrt(b*b-4*a*c))/(2*a)

fig2 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_new,X2_new_boundary)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show()

可以看出這裏只有一半曲綫，因爲X2_new_boundary 捨棄了(-b-np.sqrt(bb-4ac))/(2a)的結果

#define f(x)
def f(x):
    a = theta4
    b = theta5*x+theta2
    c = theta0+theta1*x+theta3*x*x
    X2_new_boundary1 = (-b+np.sqrt(b*b-4*a*c))/(2*a)
    X2_new_boundary2 = (-b-np.sqrt(b*b-4*a*c))/(2*a)
    return X2_new_boundary1,X2_new_boundary2

爲了把另一半補上去也方便以後的使用就封裝為一個函數

#define f(x)
def f(x):
    a = theta4
    b = theta5*x+theta2
    c = theta0+theta1*x+theta3*x*x
    X2_new_boundary1 = (-b+np.sqrt(b*b-4*a*c))/(2*a)
    X2_new_boundary2 = (-b-np.sqrt(b*b-4*a*c))/(2*a)
    return X2_new_boundary1,X2_new_boundary2

用兩個列表來接收一下

X2_new_boundary1 = [] 
X2_new_boundary2 = []
for x in X1_new:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])
print(X2_new_boundary1,X2_new_boundary2)

fig3 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_new,X2_new_boundary1)
plt.plot(X1_new,X2_new_boundary2)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show();

再可視化出來看一下，可以看出已經有了另一半就是還有個缺口

X1_range = [-0.9 + x/10000 for x in range(0,19000)]
X1_range = np.array(X1_range) #转换成数组
X2_new_boundary1 = []
X2_new_boundary2 = []
for x in X1_range:
    X2_new_boundary1.append(f(x)[0])
    X2_new_boundary2.append(f(x)[1])

爲了補齊缺口則新增一些數據補充進去

可以看到這裏的維度是19000後面也一定要用X1_range 不然就會和X2_new_boundary1對應不上就報錯了

fig3 = plt.figure()
passed=plt.scatter(data.loc[:,'test1'][mask],data.loc[:,'test2'][mask])
failed=plt.scatter(data.loc[:,'test1'][~mask],data.loc[:,'test2'][~mask])
plt.plot(X1_range,X2_new_boundary1)
plt.plot(X1_range,X2_new_boundary2)
plt.title('test1-test2')
plt.xlabel('test1')
plt.ylabel('test2')
plt.legend((passed,failed),('passed','failed'))
plt.show();

重新可視化，可以看出缺口補上了

總結

附上數據集和源碼
鏈接：https://github.com/fbozhang/python/tree/master/jupyter