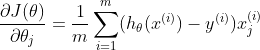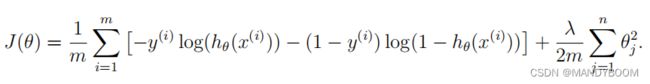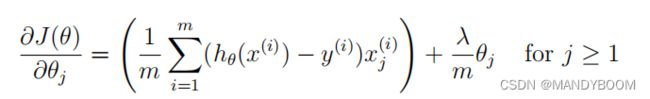第02周:吴恩达机器学习课后编程题ex2逻辑回归——Python

1 逻辑回归

在这部分练习中，您将建立一个逻辑回归模型以预测学生是否被大学录取。 假设你是一个大学部门的管理员，并且你想根据他们两次考试的成绩的情况来确定每个申请人的录取机会 。 您有以前申请人的历史数据您可以将其用作逻辑回归的训练集。 每次训练例如，您有申请人在两次考试中的成绩和录取决定。 你的任务是建立一个分类模型来估计申请人的录取概率基于这两个考试的分数。

1.1 可视化数据

其中轴是两个考试成绩，正类和负类用不同的标记显示。

• 先导入两次的成绩数据

import pandas as pd #导包

def importData():
    f = open('ex2data1.txt',encoding='utf8')##打开数据
    data = pd.read_csv(f,header=None,names=['exam01','exam02','admitted'])##将数据导入，并为变量命名
    negative = data[data['admitted'].isin(['0'])] #负类样本是没被录取的
    positive = data[data['admitted'].isin(['1'])]#正类样本是被录取的
    return negative,positive,data #返回负类值、正类值、以及整个数据集
neg,pos,data = importData() #运行上边的方法，验证是否数据正确导入了
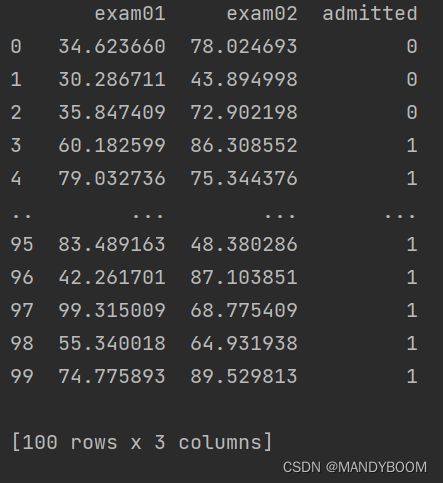
print(data) #输出看看

• 导入结果

• 可视化数据——绘制散点图（plt.scatter()） 

import matplotlib.pyplot as plt #导包

#绘制散点图
def drawScatter():
    neg, pos, data = importData()  # 运行上边的方法，获得各数据
    plt.scatter(neg['exam01'],neg['exam02'],label = 'not admitted',color = 'blue',marker='x') #画负类数据的点
    plt.scatter(pos['exam01'],pos['exam02'],label = 'admitted',color='orange',marker="*")#画正类数据得点
    plt.legend(loc = 0, ncol =1) #将图例放在数据点最少的地方，并以一列展示
    plt.xlabel('exam01score') #给x轴加上意义为第一次考试的分数
    plt.ylabel('exam02score') #给y轴加上意义为第二次考试的分数
    plt.show() #打印散点图

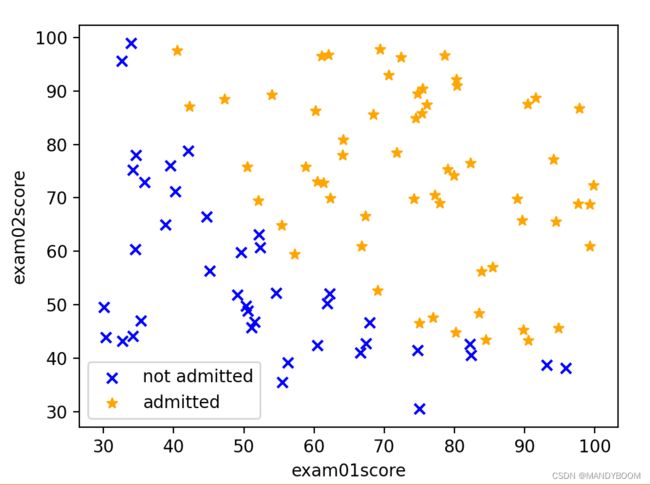
drawScatter() #运行绘制散点图的方法

• 画出来的散列图如图：

 初步可判断，这个训练集的决策边界是一根斜向下的直线，是线性的。

2.逻辑回归函数

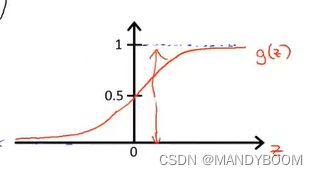
1.2.1 Warmup exercise: sigmoid function 定义sigmoid函数

              →         

import numpy as np #导包
#定义sigmoid函数
def sigmoid(z):
    return 1/(1+np.exp(-z)) #根据sigmoid函数列式

1.2.2 Cost function and gradient代价函数和梯度

吴恩达老师讲了优化后的代价函数

• 

       先定义优化后的代价函数，因为优化后的代价函数比较长，可以分成两部分，再进行计算代价函数值。

#定义代价函数
def J(theta,x,y):
    p1 = np.log(sigmoid(x.dot(theta))).dot(-y) 
    p2 = np.log(1-sigmoid(x.dot(theta))).dot(1-y)
    return (p1-p2)/(len(x))

•  定义梯度gradient，并且代价的梯度是一个与  长度相同的向量，其中第 j 个 元素（对于 j = 0, 1,...,n）定义如下：

      

        所以，梯度定义如下：

#定义梯度
def gradient(theta,x,y):
    return x.T.dot(sigmoid(x.dot(theta))-y)/(len(x))

1.2.3 Learning parameters using fminunc 学习参数

在用python实现逻辑回归和线性回归时，使用梯度下降法最小化cost function，用到了fmin_tnc()和minimize(),这两个方法都属于scipy.optimize包，故先导包。

scipy.optimize.minimize(fun, x0, args=(), method=None, jac=None, hess=None, hessp=None, bounds=None, constraints=(), tol=None, callback=None, options=None)

参数：

fun ：优化的目标函数J(θ)

x0 ：初值，一维数组，shape (n,) x0=theta

args ： 元组，可选，额外传递给优化函数的参数(x,y)

method：求解的算法，选择TNC则和fmin_tnc()类似, 截断牛顿 (TNC)算法最小化一个或多个变量的标量函数

jac：返回梯度向量的函数gradient()

import scipy.optimize as opt
def mingradient():
    neg,pos,data = importData()
    data.insert(0,'辅助向量',1)
    x = np.array(data.iloc[:,:-1])
    y = np.array(data.iloc[:,-1])
    theta = np.array(np.zeros(x.shape[1])) #theta初始化为0
    Cost = J(theta,x,y) #调用代价函数计算代价
    Gra = gradient(theta,x,y)
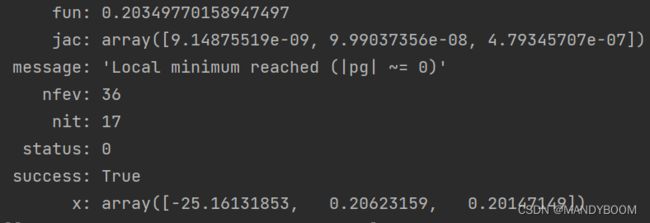
    res = opt.minimize(fun = J,x0 = theta,method = 'TNC',args=(x,y),jac = gradient)
    print(res)
    #print(x)
    #print(y)

mingradient()

结果：

其中，最后一行x:array([-25.16131853,0.20623159,0.20147149])，表示参数值，决策边界方程的参数里的三个参数。

1.2.4 Evaluating logistic regression

• 对预测准确率进行计算，对录取与不录取进行分类预测，如果预测值与实际值相等，则在correct数组中输入1，反之，在correct数组中输入0
• 先定义预测函数，根据三个参数进行预测，如果sigmoid函数算出来的大于0.5，则预测的离散值为1，若小于0.5，则预测的离散值为0

def Predict(parameter,x):
    return [1 if i >= 0.5 else 0 for i in sigmoid(x.dot(parameter))]

 计算预测的准确率

 learning_parameters = np.array([-25.1613186, 0.20623159, 0.20147149])
    predictions = Predict(learning_parameters, x) #用预测方法得到预测值的数组
    correct = [] #定义预测正确的值的数组
    for i in range(len(predictions)):
        if predictions[i] == y[i]:
            correct.append(1)
        else:
            correct.append(0)

    accuracy = sum(correct) / len(x)
    print(accuracy)

得到正确率为0.89

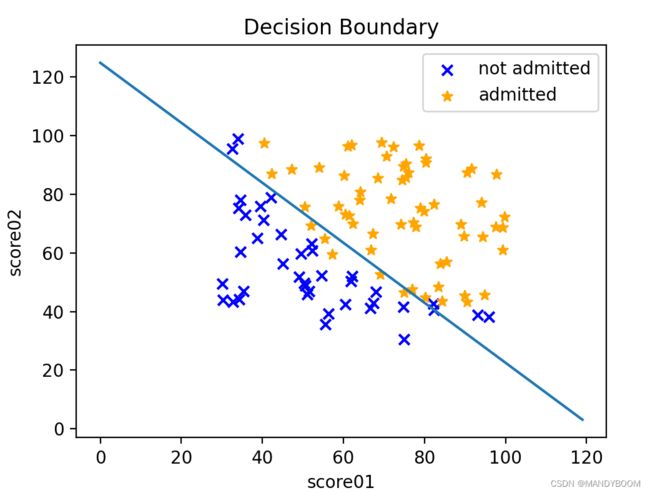
•  画出决策边界

       横坐标为成绩一x1，其范围是0~120分，通过可以算出x2,

       定义画决策边界方法：

#画出决策边界
def DrawDecisionBoundary(parameters):
    learning_parameters = parameters
    x1 = np.arange(120)
    x2 = -(learning_parameters[0]+x1*learning_parameters[1])/learning_parameters[2]
    neg,pos,data = importData()
    plt.scatter(neg['exam01'],neg['exam02'],label = 'not admitted',color='blue',marker='x' )
    plt.scatter(pos['exam01'],pos['exam02'],label = 'admitted',color='orange',marker='*' )
    plt.plot(x1,x2)
    plt.legend(loc=0,ncol=1)
    plt.title('Decision Boundary')
    plt.xlabel('score01')
    plt.ylabel('score02')
    plt.show()
learning_parameters,accuracy=mingradient()
DrawDecisionBoundary(learning_parameters)

 决策边界结果如图：

 2 Regularized logistic regression正则化逻辑回归

预测制造厂的微芯片是否通过质量保证 (QA)。 在 QA 期间，每个微芯片都经过各种测试，以确保 它运行正常。 假设你是工厂的产品经理，你有 一些微芯片在两个不同测试中的测试结果。 从这两个测试中， 您想确定是否应接受微芯片或 被拒绝。 为了帮助您做出决定，您有一个测试结果数据集 在过去的微芯片上，您可以从中构建逻辑回归模型。

2.1 Visualizing the data可视化数据

• 与上例类似，先导入数据，再画散点图

#导入数据，画出散点图
import matplotlib.pyplot as plt
import pandas as pd
def importData():
    f = open('ex2data2.txt', encoding='utf8')  ##打开数据
    data = pd.read_csv(f, header=None, names=['test01', 'test02', 'accepted'])  ##将数据导入，并为变量命名
    negative = data[data['accepted'].isin(['0'])]  # 负类样本是不合格的
    positive = data[data['accepted'].isin(['1'])]  # 正类样本是合格的
    return negative, positive, data  # 返回负类值、正类值、以及整个数据集
def visualData():
    neg,pos,data = importData()
    print(data)
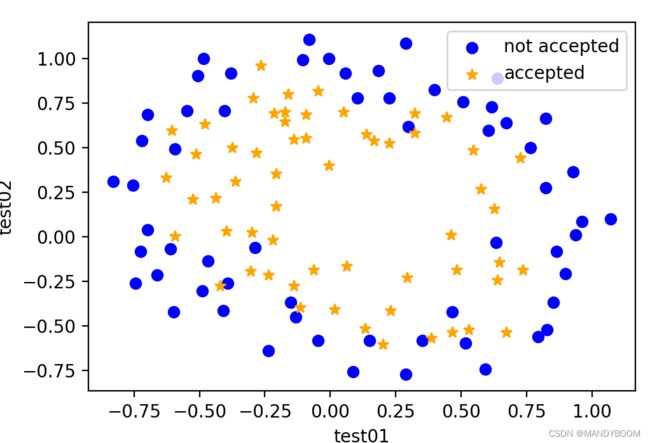
    plt.scatter(neg['test01'],neg['test02'],marker='o',color='blue',label='not accepted')
    plt.scatter(pos['test01'],pos['test02'],marker='*',color='orange',label='accepted')
    plt.legend(loc=0,ncol=1)
    plt.xlabel('test01')
    plt.ylabel('test02')
    plt.show()
    return plt
visualData()

散点图如图：

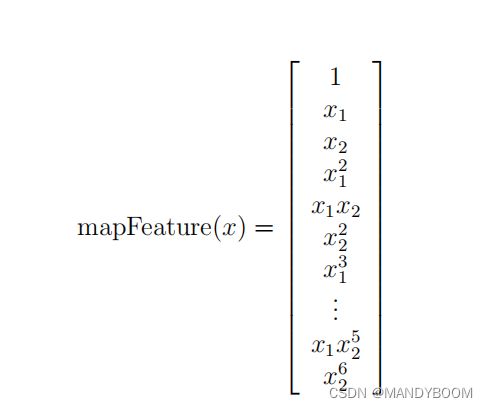
 2.2 特征映射

更好地拟合数据的一种方法是从每个数据中创建更多特征 观点。 在提供的函数 mapFeature.m 中，我们将特征映射到 x1 和 x2 的所有多项式项，直到六次方。

#定义特征映射函数
def feature_mapping(x1,x2,jie=6):
    data={}
    data={}
    for i in np.arange(jie+1):
        for p in np.arange(i+1):
            data["f{}{}".format(i-p,p)] = np.power(x1,i-p)*np.power(x2,p)
    return pd.DataFrame(data)

2.3 Cost function and gradient代价函数和梯度

• 现在将实现代码来计算成本函数和梯度正则化逻辑回归。逻辑回归中的正则化代价函数 

#将代价函数正则化
def regularizedJ(theta,x,y,Lambda=2):
    return J(theta,x,y)+(Lambda/(2*len(x)))*(theta.dot(theta))

•  正则化梯度

 

#正则化梯度
def regularizedgradient(theta,x,y,Lambda=2):
    return gradient(theta,x,y)+Lambda*theta/len(x)

 2.3.1 使用 minimize(） 学习参数

与前面部分类似，使用 minimize(） 来学习最优参数。 

import scipy.optimize as opt

neg,pos,data = importData()
fdata = feature_mapping(data['test01'],data['test02'])
x=fdata.values
y = data['accepted']
theta = np.zeros(x.shape[1])
parameters = opt.minimize(fun = regularizedJ,x0=theta,method='TNC',jac=regularizedgradient,args=(x,y,1))

theta = parameters.x
print(theta)

得到参数为：

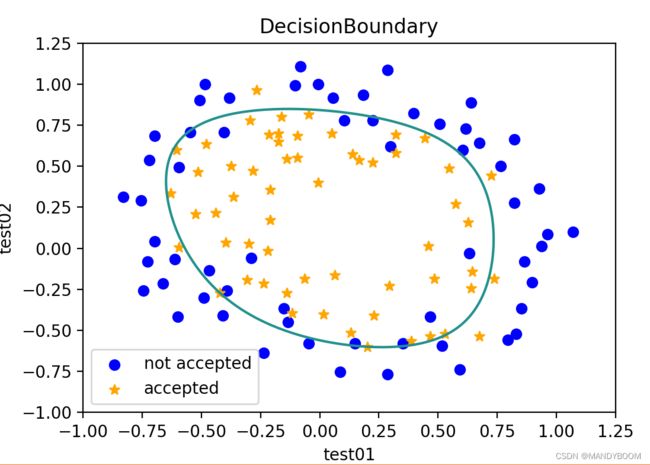
2.4 Plotting the decision boundary画出决策边界 

利用求出来的最优参数，画决策边界

def DecisionBoundary(theta):
    x=np.linspace(-1,1.25,200)
    x1,x2=np.meshgrid(x,x)
    z=feature_mapping(x1.reshape(-1),x2.reshape(-1)).dot(theta).values
    z=z.reshape(x1.shape)
    plt.scatter(neg['test01'], neg['test02'], marker='o', color='blue', label='not accepted')
    plt.scatter(pos['test01'], pos['test02'], marker='*', color='orange', label='accepted')
    plt.legend(loc=0, ncol=1)
    plt.xlabel('test01')
    plt.ylabel('test02')
    plt.title("DecisionBoundary")
    plt.contour(x1,x2,z,0)
    plt.show()

决策边界：