用matlab实现决策树算法,机器学习-ID3决策树算法（附matlab/octave代码）

ID3决策树算法是基于信息增益来构建的，信息增益可以由训练集的信息熵算得，这里举一个简单的例子

data=[心情好 天气好  出门

心情好 天气不好 出门

心情不好 天气好 出门

心情不好 天气不好 不出门]

前面两列是分类属性，最后一列是分类

分类的信息熵可以计算得到：

出门=3，不出门=1，总行数=4

分类信息熵 = -(3/4)*log2(3/4)-(1/4)*log2(1/4)

第一列属性有两类，心情好，心情不好

心情好 ,出门=2，不出门=0，行数=2

心情好信息熵=-(2/2)*log2(2/2)+(0/2)*log2(0/2)

同理

心情不好信息熵=-(1/2)*log2(1/2)-(1/2)*log2(1/2)

心情的信息增益=分类信息熵 - 心情好的概率*心情好的信息熵 - 心情不好的概率*心情不好的信息熵

由此可以得到每个属性对应的信息熵，信息熵最大的即为最优划分属性。

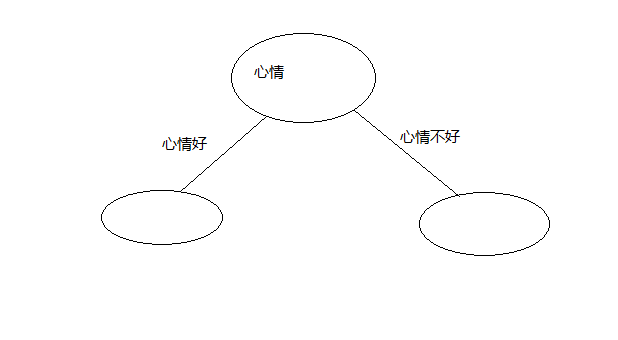
还是这个例子，加入最优划分属性为心情

然后分别在心情属性的每个具体情况下的分类是否全部为同一种，若为同一种则该节点标记为此类别，

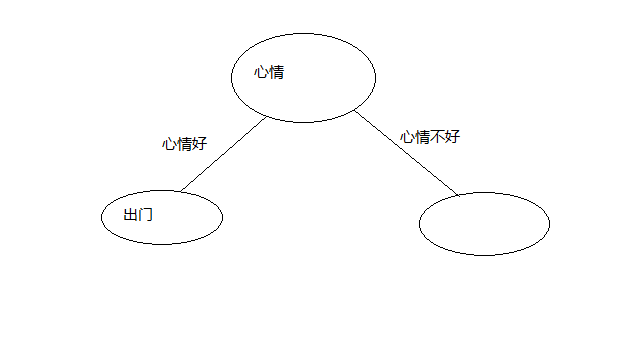
这里我们在心情好的情况下不管什么天气结果都是出门所以，有了

心情不好的情况下有不同的分类结果，继续计算在心情不好的情况下，其它属性的信息增益，

把信息增益最大的属性作为这个分支节点，这个我们只有天气这个属性，那么这个节点就是天气了，

天气属性有两种情况，如下图

在心情不好并且天气好的情况下，若分类全为同一种，则改节点标记为此类别

有训练集可以，心情不好并且天气好为出门，心情不好并且天气不好为不出门，结果入下图

对于分支节点下的属性很有可能没有数据，比如，我们假设训练集变成

data=[心情好 晴天  出门

心情好 阴天 出门

心情好 雨天 出门

心情好 雾天 出门

心情不好 晴天 出门

心情不好 雨天 不出门

心情不好 阴天 不出门]

如下图：

在心情不好的情况下，天气中并没有雾天，我们如何判断雾天到底是否出门呢？我们可以采用该样本最多的分类作为该分类，

这里天气不好的情况下，我们出门=1，不出门=2，那么这里将不出门，作为雾天的分类结果

在此我们所有属性都划分了，结束递归，我们得到了一颗非常简单的决策树。

下面附上我的实现ID3决策树算法代码：(octave/matlab，该程序本人已经验证过可以执行且结果正确，这里属性集我偷了一个懒，

没有标识出具体属性名，我是使用矩阵中的列号)

著名的还有C4.5决策树算法，它是ID3的改进，作者都是同一个人，罗斯昆兰

%生成决策树ID3算法

%data:训练集

%feature:属性集

function [node] =createTree(data,feature)

type=mostType(data);

[m,n]=size(data);

%生成节点node

%value：分类结果，若为null则表示该节点是分支节点

%name:节点划分属性

%type:节点属性值

%children:子节点

node=struct('value','null','name','null','type','null','children',[]);

temp_type=data(1,n);

temp_b=true;

for i=1:m

if temp_type!=data(i,n)

temp_b=false;

end

end

%样本中全为同一分类结果，则node节点为叶子节点

if temp_b==true

node.value=data(1,n);

return;

end

%属性集合为空，将结果标记为样本中最多的分类

if sum(feature)==0

node.value=type;

return;

end

feature_bestColumn=bestFeature(data);

best_feature=getData()(:,feature_bestColumn);

best_distinct=unique(best_feature);

best_num=length(best_distinct);

best_proc=zeros(best_num,2);

best_proc(:,1)=best_distinct(:,1);

%循环该属性的每一个值

for i=1:best_num

Dv=[];

Dv_index=1;

%为node创建一个bach_node分支，设样本data中改属性值为best_proc(i,1)的集合为Dv

bach_node=struct('value','null','name','null','type','null','children',[]);

for j=1:m

if best_proc(i,1)==data(j,feature_bestColumn)

Dv(Dv_index,:)=data(j,:);

Dv_index=Dv_index+1;

end

end

%Dv为空则将结果标记为样本中最多的分类

if length(Dv)==0

bach_node.value=type;

bach_node.type=best_proc(i,1);

bach_node.name=feature_bestColumn;

node.children(i)=bach_node;

return;

else

feature(feature_bestColumn)=0;

%递归调用createTree方法

bach_node=createTree(Dv,feature);

bach_node.type=best_proc(i,1);

bach_node.name=feature_bestColumn;

node.children(i)=bach_node;

end

end

end

%获取最优划分属性

function [column] = bestFeature(data)

[m,n]=size(data);

featureSize=n-1;

gain_proc=zeros(featureSize,2);

entropy=getEntropy(data);

for i=1:featureSize

gain_proc(i,1)=i;

gain_proc(i,2)=getGain(entropy,data,i);

end

for i=1:featureSize

if gain_proc(i,2)==max(gain_proc(:,2))

column=i;

break;

end

end

end

%计算样本最多的结果

function [res] = mostType(data)

[m,n]=size(data);

res_distinct = unique(data(:,n));

res_proc = zeros(length(res_distinct),2);

res_proc(:,1)=res_distinct(:,1);

for i=1:length(res_distinct)

for j=1:m

if res_proc(i,1)==data(j,n)

res_proc(i,2)=res_proc(i,2)+1;

end

end

end

for i=1:length(res_distinct)

if res_proc(i,2)==max(res_proc(:,2))

res=res_proc(i,1);

break;

end

end

end

%计算信息熵

function [entropy] = getEntropy(data)

entropy=0;

[m,n]=size(data);

label=data(:,n);

label_distinct=unique(label);

label_num=length(label_distinct);

proc=zeros(label_num,2);

proc(:,1)=label_distinct(:,1);

for i=1:label_num

for j=1:m

if proc(i,1)==data(j,n)

proc(i,2)=proc(i,2)+1;

end

end

proc(i,2)=proc(i,2)/m;

end

for i=1:label_num

entropy=entropy-proc(i,2)*log2(proc(i,2));

end

end

%计算信息增益

function [gain] = getGain(entropy,data,column)

[m,n]=size(data);

feature=data(:,column);

feature_distinct=unique(feature);

feature_num=length(feature_distinct);

feature_proc=zeros(feature_num,2);

feature_proc(:,1)=feature_distinct(:,1);

f_entropy=0;

for i=1:feature_num

feature_data=[];

feature_proc(:,2)=0;

feature_row=1;

for j=1:m

if feature_proc(i,1)==data(j,column)

feature_proc(i,2)=feature_proc(i,2)+1;

end

if feature_distinct(i,1)==data(j,column)

feature_data(feature_row,:)=data(j,:);

feature_row=feature_row+1;

end

end

f_entropy=f_entropy+feature_proc(i,2)/m*getEntropy(feature_data);

end

gain=entropy-f_entropy;