【计算机图形学】【MacOS Xcode】【实验报告】OpenGL下的图形变换、Cohen-sutherland算法、改进的Cohen-sutherland算法

实  验  报  告

一、实验目的

1. 掌握图形的二维基本几何变换，如平移、旋转、缩放、对称、错切变换；
2. 掌握OpenGL中模型变换函数的功能及使用方法；
3. 掌握基本的图形裁剪算法的思想，会编写程序实现算法的应用；
4. 进一步学习并掌握鼠标、键盘交互；

---

二、实验内容与实验步骤

任务一：

• 绘制三角形相对于一条直线方程y = 50 – x对称的图形。

思路：将三角形平移、旋转、翻转、反向旋转、反向平移的顺序，利用gltranslatef()、glrotatef()、glscalef()函数将三角形乘上变换矩阵，最终实现关于直线对称的功能。

• 绘制以三角形的顶点（0.0，25.0）为原点将三角形旋转30度和-45度的图形。

思路：利用gltranslatef()、glrotatef()函数，将三角形平移、旋转、反向平移，实现三角形绕定点旋转的效果。

任务二：

• 绘制旋转缩小正方形

思路：先绘制第一个最大的矩形，其次设计缩小旋转函数，使矩形绕坐标原点进行旋转的同时在框内生成三角形，其中正方形的底边分割比例为1:4。设计键盘交互控制函数，使每次按键A时可以生成一个新的缩小旋转正方形。

• 绘制旋转风车

思路：利用对矩形的错切运算生成单个风车扇叶，利用旋转运算使其生成三个扇叶构成一个完整的风车。设计鼠标交互函数，实现点击左键风车转动，点击右键停止的功能。

任务三：改进的Cohen-sutherland算法

裁剪线段原理：首先将窗口区域分为9个部分，每个部分给一个区域码，然后计算线段两端端点的区域码，根据区域码来选择抛弃线段。之后利用中点中点分割法代替Cohen-sutherland算法中的“计算直线段与窗口边界的交点”的步骤，实现取交功能。

实现思路：先对线段的端点所在的位置进行编码，根据编码判断全取或全弃，如果不能全取或全弃则用中点分割算法进一步求解是否有交点。

---

三、实验环境

1. 操作系统：macOS Big Sur Version 11.6
2. 调试软件：Xcode Version 13.0
3. 上机地点：xxx
4. 机器台号：xxx

---

四、实验过程与分析

任务一：

• 绘制三角形相对于一条直线方程y = 50 – x对称的图形。

主要代码：

void display(void)
{
    glClear (GL_COLOR_BUFFER_BIT);
    glLoadIdentity ();
    glColor3f (1.0, 0.7, 0.8);
    draw_axis();
    glColor3f (1.0, 1.0, 1.0);
    draw_line();
    draw_triangle ();
    
    glLineStipple (1, 0x8888);
    glLoadIdentity ();
    glTranslatef (50.0, 0.0, 0.0); //平移
    glRotatef (-45.0, 0.0, 0.0, 1.0); //旋转
    glScalef (1.0, -1.0, 1.0); //对称
    glRotatef (45.0, 0.0, 0.0, 1.0);
    glTranslatef (-50.0, 0.0, 0.0);
    draw_line();
    draw_triangle ();
    glFlush ();
}

• 绘制三角形相对于一条直线方程y = 50 – x对称的图形。               

主要代码：

void display(void)
{
    glClear (GL_COLOR_BUFFER_BIT);
    glLoadIdentity ();
    glColor3f (1.0, 0.7, 0.8);
    draw_axis();
    glColor3f (1.0, 1.0, 1.0);
    glLineStipple (1, 0x8888);
    draw_triangle ();

    glEnable (GL_LINE_STIPPLE);
    glLineStipple (1, 0xF00F);
    glLoadIdentity ();
    glTranslatef (0.0, 25.0, 0.0); //平移
    glRotatef (-45.0, 0.0, 0.0, 1.0); //旋转
    glTranslatef (0.0, -25.0, 0.0);
    draw_triangle ();
    
    glLoadIdentity ();
    glTranslatef (0.0, 25.0, 0.0); //平移
    glRotatef (30.0, 0.0, 0.0, 1.0); //旋转
    glTranslatef (0.0, -25.0, 0.0);
    draw_triangle ();

    glFlush ();
}

---

任务二：

• 绘制旋转缩小正方形

主要代码：

void rotate(void)
{
    a = a * (sqrt(10) / 4);
    b = b * (sqrt(10) / 4);
    c = c * (sqrt(10) / 4);
    d = d * (sqrt(10) / 4);
    spin = spin -(45-(atan(4)/PI*360));
    if (spin > 360.0)
        spin = spin - 360.0;
    glutPostRedisplay();
}

void keyboard(unsigned char key, int x,int y) {
    switch (key) {
    case'a':
        rotate();
        break;
    case'c':
        glutIdleFunc(NULL);
        break;
    default:
        break;
    }
    glutPostRedisplay();
}

• 绘制旋转风车

主要代码：

static GLfloat spin = 0.0;

void draw_part(void){
    glBegin(GL_QUAD_STRIP);
    glVertex2f(0,0);
    glVertex2f(0,20);
    glVertex2f(20,0);
    glVertex2f(20,20);
    glEnd();
}
void draw_thing() {//根据参数错切为菱形并绘制图形
    float a = sqrt(3)/4;
    float arr[16]={
        1,0,0,0,
        a,1,0,0,
        0,0,1,0,
        0,0,0,1
    };
    glMultMatrixf(arr);
    draw_part();
    glEnd();
}

void draw_thing2(void) {//绘制风车
    glClear(GL_COLOR_BUFFER_BIT);
//    glLoadIdentity();
    glColor3f(1.0, 0, 0);
    glRotatef(spin, 0.0, 0.0, 1.0);
    draw_thing();


//
    glLoadIdentity();
    glColor3f(0, 1.0, 0);
    glRotatef(120, 0.0, 0.0, 1.0);
    glRotatef(spin, 0.0, 0.0, 1.0);
    draw_thing();

    glLoadIdentity();
    glColor3f(0, 0, 1.0);
    glRotatef(240, 0.0, 0.0, 1.0);
    glRotatef(spin, 0.0, 0.0, 1.0);

    draw_thing();

    glDisable(GL_LINE_STIPPLE);
    glFlush();


}

void display(void)
{
    glClear(GL_COLOR_BUFFER_BIT);
    glPushMatrix();
    draw_thing2();
    glPopMatrix();
    glutSwapBuffers();
}

void spinDisplay(void)
{
    spin = spin + 0.5;
    if (spin > 360.0)
        spin = spin - 360.0;
    glutPostRedisplay();
}

---

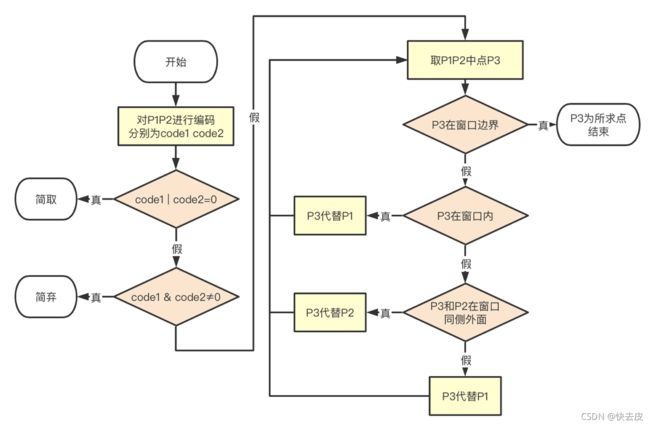
任务三（改进的Cohen-sutherland算法）：

流程图：（求距离P1最远的可见点，P2同理）

 【还尝试了经典的Cohen-sutherland算法，即求交点的方法】

代码：

// classic_Cohen-sutherland
// 经典Cohen-sutherland算法

#define GL_SILENCE_DEPRECATION

#include 
#include 
#include 

#define LEFT 1
#define RIGHT 2
#define BOTTOM 4
#define TOP 8

using namespace std;



class ObjPoint{
public:
    ObjPoint(int xv, int yv):x(xv), y(yv) {}
    int x;
    int y;
};

class ObjLine{
public:
    ObjLine(ObjPoint p1v, ObjPoint p2v):
    p1(p1v.x, p1v.y), p2(p2v.x, p2v.y){}
    ObjPoint p1;
    ObjPoint p2;
};

class ObjRect{
public:
    ObjRect(int x1, int x2, int y1, int y2):xl(x1), xr(x2), yb(y1), yt(y2){}
    int xl;
    int xr;
    int yb;
    int yt;
};



// global variables
int cut_status = 0;
vector lines;
vector cutlines;

void init(void)
{
    glClearColor (0.0, 0.0, 0.0, 0.0);
    glShadeModel (GL_FLAT);
}
void draw_triangle(void)
{ //绘制一个三角形
    glBegin (GL_LINE_LOOP);
    glVertex2f(0.0, 25.0);
    glVertex2f(25.0, -25.0);
    glVertex2f(-25.0, -25.0);
    glEnd();
}
void draw_rec(int l, int r, int b, int t)
{ //绘制一个矩形
    glBegin (GL_LINE_LOOP);
    glVertex2f(l,b);
    glVertex2f(l,t);
    glVertex2f(r,t);
    glVertex2f(r,b);
    
    glEnd();
}

// 求编码
// 0xFF 1111 1111
// 0x01 0000 0001
GLbyte code(ObjPoint p1, ObjRect w)
{
    GLbyte pcode = 0;
    //上下右左
    // 左边界的左侧
    if(p1.x < w.xl){
        pcode = pcode | 0x01;
    }
    // 上边界的上侧
    if(p1.y > w.yt){
        pcode = pcode | 0x08;
    }
    // 右边界的右侧
    if(p1.x > w.xr){
        pcode = pcode | 0x02;
    }
    // 下边界的下侧
    if(p1.y < w.yb){
        pcode = pcode | 0x04;
    }
    
    return pcode;
}

int far(ObjPoint p1, ObjPoint p2, ObjPoint& pf, ObjRect w)
{
    return 0;
}


void cut(ObjRect w)
{
    for(int i=0; i

// improved_Cohen-sutherland
// 改进的Cohen-sutherland算法

#define GL_SILENCE_DEPRECATION

#include 
#include 
#include 
using namespace std;
#include 
#include 
#define DIST(x1,y1,x2,y2)  sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2))
//class
class ObjPoint {
public:
    ObjPoint() {};
    ObjPoint(int xv, int yv) :x(xv), y(yv) {};
    int x;
    int y;
};
class ObjLine {
public:
    ObjLine(ObjPoint p1v, ObjPoint p2v) :p1(p1v), p2(p2v) {};
    ObjPoint p1;
    ObjPoint p2;
};
class ObjRect{
public:
    ObjRect(int x1, int x2, int y1, int y2):xl(x1), xr(x2), yb(y1), yt(y2){}
    int xl;
    int xr;
    int yb;
    int yt;
};
//global variables
int cut_status = 0;
vector lines;
vector cutlines;

void draw_rec(int l, int r, int b, int t)
{ //绘制一个矩形
  glBegin (GL_LINE_LOOP);
  glVertex2f(l,b);
  glVertex2f(l,t);
  glVertex2f(r,t);
glVertex2f(r,b);
    
  glEnd();
}
void init(void)
{
    glClearColor(0.0, 0.0, 0.0, 0.0);
    glShadeModel(GL_FLAT);
}
GLbyte code(ObjPoint p1, ObjRect w) {
    GLbyte pcode = 0;

    // 左边界的左侧
    if(p1.x < w.xl){
        pcode = pcode | 0x01;
    }
    // 上边界的上侧
    if(p1.y > w.yt){
        pcode = pcode | 0x08;
    }
    // 右边界的右侧
    if(p1.x > w.xr){
        pcode = pcode | 0x02;
    }
    // 下边界的下侧
    if(p1.y < w.yb){
        pcode = pcode | 0x04;
    }
    
    return pcode;
}
int far(ObjPoint p1, ObjPoint p2, ObjPoint& pf, ObjRect w) {
    long dist;
    ObjPoint pm;
    GLbyte p1code, p2code, pmcode;
    p1code = code(p1, w);
    p2code = code(p2, w);
    if (p2code == 0) {
        pf = p2;
        return 0;
    }
    dist = DIST(p1.x, p1.y, p2.x, p2.y);
    while (dist > 1) {
        p1code = code(p1, w);
        p2code = code(p2, w);
        if ((p1code & p2code) != 0) return 1;
        pm.x = (p1.x + p2.x) / 2;
        pm.y = (p1.y + p2.y) / 2;
        pmcode = code(pm, w);
        if (pmcode == 0) {
            p1 = pm;
        }
        else if ((p1code & pmcode) != 0) {
            p1 = pm;
        }
        else if ((p2code & pmcode) != 0) {
            p2 = pm;
        }
        dist = DIST(p1.x, p1.y, p2.x, p2.y);
    }
    pf = pm;
    return 0;
}
void cut(ObjRect w) {
    unsigned int i = 0;
    ObjPoint p1;
    ObjPoint p2;
    ObjPoint pf;
    GLbyte p1code;
    GLbyte p2code;
    cutlines.clear();//清空
    for (i = 0; i < lines.size(); i++) {
        //lines.[i]
        //求编码
        p1 = lines[i].p1;
        p2 = lines[i].p2;
        p1code = code(p1, w);
        p2code = code(p2, w);
        //1.判断全取
        if ((p1code | p2code) == 0) {
            cutlines.push_back(lines[i]);
            continue;
        }
        //2.可能有交点
        else if ((p1code & p2code) == 0) {
            //p1 p2 最远可见点
            if (far(p1, p2, pf, w))continue;
            //p1 p2 交换
            p2 = p1;
            p1 = pf;
            //p1 p2 最远可见点
            if (far(p1, p2, pf, w))continue;
            //可见段p1 pf放进cutlines
            cutlines.push_back(ObjLine(p1, pf));
        }
        //3.全弃
    }
}
void draw_line(void)
{ //绘制一条线
    unsigned int i;
    glPolygonMode(GL_FRONT, GL_LINE);
    glRectf(100, 400, 100, 600);
    if (cut_status == 0) {
        for ( i = 0; i < lines.size(); i++) {
            glBegin(GL_LINES);
            glVertex2f(lines[i].p1.x, lines[i].p1.y);
            glVertex2f(lines[i].p2.x, lines[i].p2.y);
            glEnd();
        }
    }
    else {
        cut(ObjRect(100, 400, 100, 600));
        for (int i = 0; i < cutlines.size(); i++) {
            glBegin(GL_LINES);
            glVertex2f(cutlines[i].p1.x, cutlines[i].p1.y);
            glVertex2f(cutlines[i].p2.x, cutlines[i].p2.y);
            glEnd();
        }
    }

}

void keyboard(unsigned char key, int x, int y) {
    switch (key) {
    case 'o':
        cut_status = 0;
        break;
    case 'c':
        cut_status = 1;
        break;
    }
    glutPostRedisplay();
}
void display(void)
{
    glClear(GL_COLOR_BUFFER_BIT);
    glLoadIdentity();
    glColor3f(1.0, 1.0, 1.0);
    draw_rec(100, 400, 100, 600);
    draw_line();
    glFlush();
}
void reshape(int w, int h)
{
    glViewport(0, 0, (GLsizei)w, (GLsizei)h);
    glMatrixMode(GL_PROJECTION);
    glLoadIdentity();
    if (w <= h)
    gluOrtho2D (0, 800, 0*(GLfloat)h/(GLfloat)w,800.0*(GLfloat)h/(GLfloat)w);
    else
    gluOrtho2D (0.0*(GLfloat)w/(GLfloat)h,
    800.0*(GLfloat)w/(GLfloat)h, 0.0, 800.0);
    glMatrixMode(GL_MODELVIEW);
}

int main(int argc, char** argv)
{
    glutInit(&argc, argv);
    glutInitDisplayMode (GLUT_SINGLE | GLUT_RGB);
    glutInitWindowSize (300, 400);
    glutInitWindowPosition (100, 100);
    glutCreateWindow (argv[0]);
    init ();

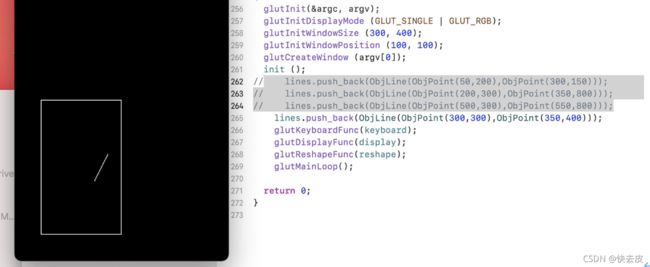
    lines.push_back(ObjLine(ObjPoint(50,200),ObjPoint(300,150)));
    lines.push_back(ObjLine(ObjPoint(200,300),ObjPoint(350,800)));
    lines.push_back(ObjLine(ObjPoint(500,300),ObjPoint(550,800)));
    lines.push_back(ObjLine(ObjPoint(300,300),ObjPoint(350,400)));
    glutKeyboardFunc(keyboard);
    glutDisplayFunc(display);
    glutReshapeFunc(reshape);
    glutMainLoop();

  return 0;
}

---

五、实验结果总结（包括Bug调试）

任务一：

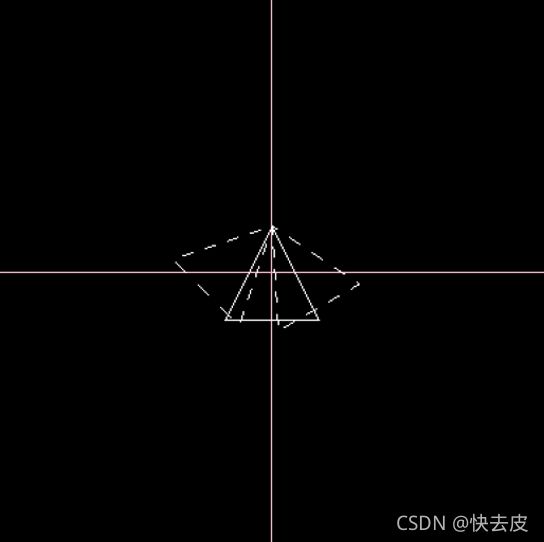
• 绘制三角形相对于一条直线方程y = 50 – x对称的图形。

之前调试都是一步一步看的，看ppt上说旋转要绕着原点转，一直在纠结怎么绕着原点转，耽误了很久。因为OpenGL中的变换操作都是对整个坐标系一起操作的，每次平移时坐标系也会跟着动，让我十分迷茫和困惑。后来才想到，应该从整体来看，如果说变换的前半部分做不到控制坐标轴不变，只需要在变换后半的恢复部分同样随着坐标系一起动就可以了，说明解决问题还是应该有大局意识，不能说看资料中一步一步的操作就一定要按部就班。

运行截图：

 中间步骤：

•  绘制以三角形的顶点（0.0，25.0）为原点将三角形旋转30度和-45度的图形。

规律：期待按哪个点旋转，就将其x、y、z值输入第一个gltranslatef()函数作为参数，再调用glrotatef()函数旋转即可。

运行结果：

 任务二：

• 绘制旋转缩小正方形

初始代码：

void draw_recs(){
    for(int i=0; i<10; i++){

        glRotatef (18.44, 0.0, 0.0, 1.0); //旋转
        glScalef (0.78, 0.78, 1.0); //对称
        
        if(cut_status==1){
            //glLoadIdentity ();
            draw_rec();
        }
    }
}

运行结果：

按键前：

按键后： 

问题1：无法实现点一次“a”键绘制一个新正方体的功能，而是按一下就全部出来了。

原因：在第一次按键时，cut_status便为1，之后再按无法起作用。

改进：改变策略，在键盘交互的函数中直接调用绘制函数。

修改代码：

void keyboard(unsigned char key, int x,int y) {
    switch (key) {
    case'a':
        rotate();
        break;
    case'c':
        glutIdleFunc(NULL);
        break;
    default:
        break;
    }
    glutPostRedisplay();
}

问题2：这里分割的比例是通过运算和大致感觉“凑”出来的，不怎么精准。

修改代码：

void rotate(void)
{
    a = a * (sqrt(10) / 4);
    b = b * (sqrt(10) / 4);
    c = c * (sqrt(10) / 4);
    d = d * (sqrt(10) / 4);
    spin = spin -(45-(atan(4)/PI*360));
    if (spin > 360.0)
        spin = spin - 360.0;
    glutPostRedisplay();
}

运行结果：最终效果如前，但每按一次键盘才会生成一次图形。

---

• 绘制旋转风车

问题：最开始想将正方形错切成为菱形时采用了glscalef()函数，然而这个函数应该用于不同坐标轴的按比例缩放。

运行结果：

改进：创建数组，采用矩阵乘法进行错切。引入arr[9]创建三阶矩阵，通过改变变换矩阵中的值，可以实现沿x轴方向错切。

问题：没有反应，还是同原来一样的正方形。

错误原因猜想：由于在旋转、平移的时候，glrotate()和gltranslate()两个函数都输入了三个坐标参数，分别代表在x轴、y轴、z轴上的数值，因此构造变换矩阵时应当采用四阶矩阵输入。

改进：用arr[16]创建四阶矩阵，通过变换矩阵中的值可以使图形沿x错切。

代码：

void draw_thing() {//根据参数错切为菱形并绘制图形
    float a = sqrt(3)/4;
    float arr[16]={
        1,0,0,0,
        a,1,0,0,
        0,0,1,0,
        0,0,0,1
    };
    glMultMatrixf(arr);
    draw_part();
    glEnd();
}

运行结果：（旋转的）

创新：利用圆形以及对其错切、旋转、改变颜色，可以得到一朵旋转的花。

代码：

void draw_part(void){
//    glBegin(GL_QUAD_STRIP);
//    glVertex2f(0,0);
//    glVertex2f(0,20);
//    glVertex2f(20,0);
//    glVertex2f(20,20);
//    glEnd();
    float R = 10.0f;
    int n = 80;     //这里的n表示用多边形绘制圆的精度，可以考虑增大精度
    glBegin(GL_POLYGON);
    /*
        表示对以下画出的点进行的操作，这里是形成多边形
        类似的还有GL_LINE_STRIP、GL_LINE_LOOP、GL_POINT等
    */
    for (int i = 0; i < n; i++)     //通过数学计算来画多边形的点
    {
        glVertex2f(R*cos(2 * PI*i / n), R*sin(2 * PI*i / n));
    }
    glEnd();
}

 运行结果：（旋转的）

---

 任务三（改进的Cohen-sutherland算法）：

最开始写了一个经典Cohen-sutherland的裁剪方法，并且用的是之前图形作为测试样例。

按键前：

 按键后：

问题：只能裁一半，并且非题目要求的图形。

修改：将自定义的图形换成题目要求的图形，并利用循环，交换p1code和p2code。

修改代码：（此处用的是经典Cohen-sutherland算法，求交点计算边界点）

void cut(ObjRect w)
{
    unsigned int i;
    ObjPoint p1(0,0);
    ObjPoint p2(0,0);
    ObjPoint pf(0,0);
    GLbyte pcode, p1code, p2code;
    
    for(i=0; i

改进代码： 

 测试样例：

ObjLine(ObjPoint(50,200),ObjPoint(300,150))
ObjLine(ObjPoint(200,300),ObjPoint(350,800))
ObjLine(ObjPoint(500,300),ObjPoint(550,800))
ObjLine(ObjPoint(300,300),ObjPoint(350,400))

运行结果：

按键前：

 

问题：内部的线也裁剪没了。并且，仅显示内部这条线的时候，又不会被剪切。

错误原因猜想：应该是由于变量声明放在了循环之前，上一个直线的点如果没有更新值将会被放入下一条直线中。而“简取”就是没有更新值的一种情况，因此按照上一条直线做了处理，被裁剪掉了。

改进：将其放入循环之内。

结果：不对。。区域内的还是会被裁剪。

解决：尝试只在这类情况中进行裁剪，结果当只留这一条线的时候，它并不会被裁剪。

Debug代码：

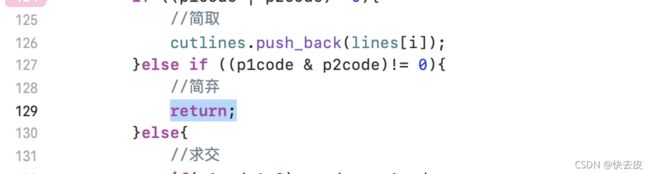
发现是由于这条线之前是“简弃”的情形，采用了return，使后面的步骤出了问题。

错误代码：

解决方案：将其删去。

多加一条测试线：

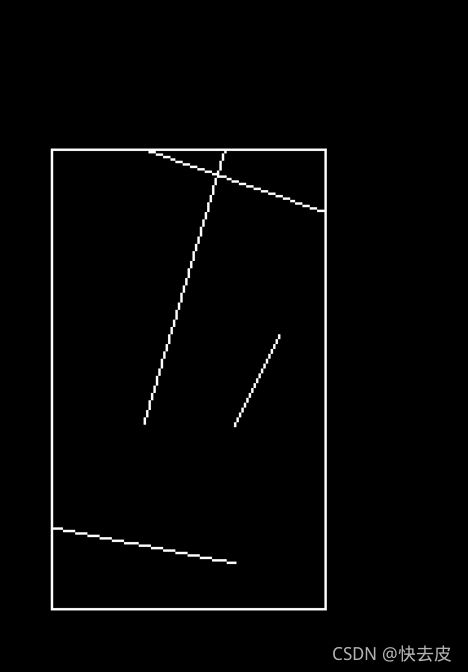
(ObjPoint(500,500),ObjPoint(150,620))

最终：

按键盘“o”时：

 按键盘“c”时：

 之后采用改进的Cohen-sutherland算法又进行了裁剪尝试，同老师课上讲的相同，代码见前文，运行结果同上。

---

六、附录

Q：和Liang-Barsky算法对比，改进的Cohen-sutherland算法有什么优点？

1. Cohen-sutherland算法用编码方法实现了对完全可见和不可见直线段的快速接受和拒绝
2. Cohen-sutherland算法主要计算过程只用到加法或位移运算，易于硬件实现，同时适合于并行计算。

Q：和在三维空间中怎样利用Liang-Barsky算法实现对于一个长方体的视体积的线段裁剪？

A：提升一个维度，将线与线的交点判断转换为与截面的相交判断。将长方体的面分为三个入面三个出面，然后将三维线段写成参数方程，参照二维梁友栋算法进行交点的判断。

Q：编写OpenGL程序对几何图形进行坐标变换时调用变换的顺序和实际变换的顺序是否一致？

A：不一致。OpenGL的变换函数最后调用函数的是最先应用的矩阵，所以看复合矩阵代码时应该从下往上看才是正确的矩阵应用顺序。从数学语言来说就是从上到下矩阵依次右乘于前一个矩阵。

---

有错误欢迎指出，用到了麻烦点个赞点个关注～～