吴恩达机器学习课程笔记一

通用人工智能—AGI

机器学习—机器无需明确编程即可学习的研究领域(非正式定义)

前言

监督学习—Supervised learning

监督学习指的是数据集有输出标签,每个数据样本都有输出标签—right answers，监督学习在实际应用中使用较多

监督学习主要有分类---Classification和回归---Regression两大类别，分类和回归都是对输入进行预测，不同之处在于分类预测的结果是有限的（一组有限的可能输出类别），而回归预测的结果是无限的(如经典的房价预测)

无监督学习—Unsupervised learning

区别与监督学习，无监督学习的数据没有标签。因为没有数据标签，无监督学习并没有预测功能，我们使用无监督学习算法来找到数据集中的某种结构或某种模式，或者只是找到数据中一些有趣的特性。这就是无监督学习，并不是试图监督算法给每个输入一个正确的答案。

无监督学习可能决定数据可以分为不同的组或者集群，

聚类

将相似的数据点聚集在一起

异常检测

用于检测异常事件

降维

压缩大的数据集得到小数据集，并且丢失尽可能少的信息

增强学习—Reinforcement learning

Linear regression

一些机器学习的名词

$$\begin{gathered} 线性回归模型---一条拟合数据的直线 \\ 输入变量x---feature(特征) \\ 输出变量y---target(目标) \\ x(输入特征)⟶f(model:模型)⟶\hat{y}(评估预测的结果) \\ 算法预测结果:\hat{y}或者y-hat,\hat{y}是对正确结果y的估计或者预测 \end{gathered}$$

最主要的是如何构建 模型：f

参考博客

一元线性回归_Chen的博客的博客-CSDN博客_一元线性回归法

损失函数

为了实现线性回归，关键步骤是定义一个损失函数（cost function）
$$\begin{gathered} 损失函数J(w,b)=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^{(i)}-y^{(i)}{)}^2 \\ 为什么要除以2m?:如果不除于m，损失函数值会随着样本数增加而变大，除以2应该是为了方便下一步计算，约去系数 \end{gathered}$$
平方差成本函数是线性回归最普遍的损失函数

我们要求得使得损失函数最小的参数 w 和 b

线性回归的平方差成本函数只有一个全局最小值，是一个凸函数

参考博客

单变量梯度下降_Chen的博客的博客-CSDN博客

梯度下降的实现

$$\begin{gathered} w=w-\alpha \frac{\partial }{\partial w}J(w,b) \\ \alpha (Learningrate):学习率，通常取值在0-1之间，通俗的说\alpha 决定了你下坡的幅度， \\ \alpha 非常大代表着下坡时迈出一大步，\alpha 过小则迈小步下坡，如何选择一个合适的\alpha 是个问题 \\ \frac{\partial }{\partial w}J(w,b):代表着往哪个方向下坡 \\ 此外，b=b-\alpha \frac{\partial }{\partial b}J(w,b) \\ 重复上面两个不断更新的步骤，直到算法收敛，达到算法的局部最小值 \\ 如何同时更新w和b(更新其中一个，另一个不受影响)呢? \\ temp\_w=w-\alpha \frac{\partial }{\partial w}J(w,b) \\ temp\_b=b-\alpha \frac{\partial }{\partial b}J(w,b) \\ w=temp\_w \\ b=temp\_b \\ 梯度下降的正确方式是参数同时更新 \end{gathered}$$

学习率alpha的选择

学习率过小

学习率过小，梯度下降算法照样可以起作用，但是需要重复很多的步骤，需要花费大量的时间

学习率过大

学习率过大可能永远都不会找到局部最小值，变量不能收敛，甚至可能使得变量发散

线性回归的梯度下降求法

$$\begin{gathered} 线性回归模型:f_{w,b}=wx+b \\ 损失函数:J(w,b)=\frac{1}{2m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}{)}^2 \\ 梯度下降算法: \\ temp\_w=w-\alpha \frac{\partial }{\partial w}J(w,b),其中\frac{\partial }{\partial w}J(w,b)=\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)} \\ temp\_b=b-\alpha \frac{\partial }{\partial b}J(w,b),其中\frac{\partial }{\partial b}J(w,b)=\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}) \\ w=temp\_w \\ b=temp\_b \end{gathered}$$

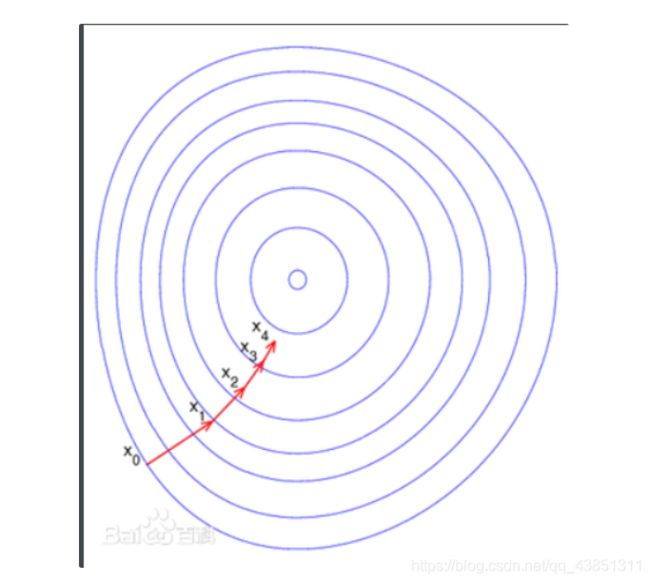
线性回归的平方差损失函数只有一个局部局最小值，即全局最小值，是一个凸函数

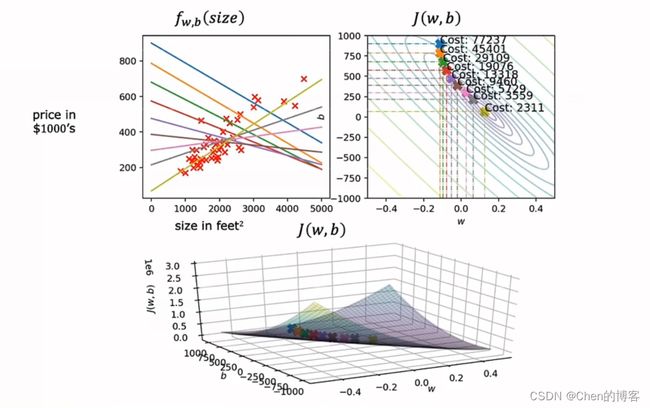
下图为梯度下降的过程图：

左上图为模型和数据图，右上为损失函数等高线图，下图为损失函数表面图

Multiple linear regression

多特征线性回归

考虑更加复杂，更加符合实际的线性回归–特征变多
$$\begin{gathered} x_2^{(3)}表示第3个样本点的第2个特征 \\ {f}_{w,b}(x)=w_1{x}_1+w_2{x}_2+w_3{x}_3+......+w_n{x}_n+b \\ 向量w=[w_1,w_2,w_3....w_n] \\ b表示数字，不是向量 \\ x=[x_1,x_2,x_3....x_n] \\ {f}_{w,b}(x)=w\ast x+b=w_1{x}_1+w_2{x}_2+w_3{x}_3+......+w_n{x}_n+b \end{gathered}$$

向量化

$$\begin{gathered} 现实生活中，线性回归问题的变量，都不止包含一个特征值，即x_1,x_2,x_3.....， \\ {f}_{w,b}(x)=w_1{x}_1+w_2{x}_2+w_3{x}_3+......+w_n{x}_n+b \\ 可以用向量来表示: \\ x=\left[\begin{array}{c}{x}_1,x_2,x_3.....x_n\end{array}\right] \\ 同样，w也要变为w=\left[\begin{array}{c}{w}_1,w_2,w_3.....w_n\end{array}\right] \\ 其中，x_2^{(3)}表示第3个样本点的第2个特征 \\ {f}_{w,b}(x)=w\ast x+b \end{gathered}$$

向量化可以使得代码更短，运行更加高效

Python中，使用numpy包

w=np.array([1.0,2.5,-3.3])
b=4
x=np.array([10,20,30])

$$\begin{gathered} f_{w,b}(x)=w\ast x+b=w_1{x}_1+w_2{x}_2+w_3{x}_3+......+w_n{x}_n+b \\ 没有向量化的情况: \\ (1)f=w[0]\ast x[0]+ \\ w[1]\ast x[1]+ \\ w[2]\ast x[2]+b \\ (2)f_{w,b}(x)=\sum _{j=1}^n{w}_j{x}_j+b \\ f=0 \\ forjinrange(0,n): \\ f=f+w[j]\ast x[j] \\ f=f+b \\ 向量化后: \\ w=\left[\begin{array}{c}{w}_1,w_2,w_3.....w_n\end{array}\right] \\ x=\left[\begin{array}{c}{x}_1,x_2,x_3.....x_n\end{array}\right] \\ {f}_{w,b}(x)=w\ast x+b \\ 只需要一行代码即可 \\ f=np.dot(w,x)+b \\ 向量化后不仅代码变短，而且代码的运行速度比上面两种都要快，原因是numpy可以使用GPU来加速矩阵运算 \\ 计算机可以并行的将每个w_i\ast x_i,再使用专门的硬件高效求和\sum _{i=1}^n{w}_i\ast x_i \end{gathered}$$

向量化在多元线性回归中的显著作用：
$$\begin{gathered} w=\left[\begin{array}{c}{w}_1,w_2,w_3.....w_n\end{array}\right] \\ d=\left[\begin{array}{c}{d}_1,d_2,d_3.....d_n\end{array}\right],d_i为关于w_i的偏导 \\ {w}_j=w_j-\alpha d_j(j=1-n) \\ 没有矢量化的情况: \end{gathered}$$

for  in range(0,n):
    w[j]=w[j]-alpha*d[j]

$$\begin{gathered} 在并行情况下，w_{i\sim n}并行的减去\alpha \ast d_{i\sim n},而不需要依次的计算 \\ {w}_{i\sim n}=w_{i\sim n}-\alpha \ast d_{i\sim n} \end{gathered}$$

当特征非常多或者数据集非常大时，矢量化后用numpy加速计算就会很有用

多元线性回归的梯度下降

$$\begin{gathered} f_{w,b}(x)=w\ast x+b=w_1{x}_1+w_2{x}_2+w_3{x}_3+......+w_n{x}_n+b \\ {f}_{w,b}(x)=w\ast x+b \\ 损失函数:J(w_1,...,w_n,b)=J(w,b)=\frac{1}{2m}\sum _{i=1}^m(w^{}\ast x^{(i)}+b-y^{(i)}{)}^2 \\ temp\_w_j=w_j-\alpha \frac{\partial }{\partial w_j}J(w_1,..w_n,b) \\ temp\_b=b-\alpha \frac{\partial }{\partial b}J(w_1,..w_n,b) \\ 可以写成: \\ temp\_w_j=w_j-\alpha \frac{\partial }{\partial w_j}J(w,b) \\ temp\_b=b-\alpha \frac{\partial }{\partial b}J(w,b) \end{gathered}$$

单个特征和多个特征的参数w , b 迭代过程的对比:
$$\begin{gathered} 单个特征下参数更新情况: \\ w=w-\alpha \frac{1}{m}(f_{w,b}(x^{(i)})-y^{(i)})x^{(i)} \\ b=b-\alpha \frac{1}{m}(f_{w,b}(x^{(i)})-y^{(i)}) \\ 这里的x^{(i)}只有一个特征，即没有下标 \\ 多个特征下(n\ge 2)时，参数更新: \\ {w}_1=w_1-\alpha \frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x_1^{(i)},其中\frac{\partial }{\partial w_j}J(w,b)=\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x_1^{(i)} \\ {w}_n=w_n-\alpha \frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x_n^{(i)} \\ b=b-\alpha \frac{1}{m}(f_{w,b}(x^{(i)})-y^{(i)}) \end{gathered}$$
梯度下降是最小化损失函数 J， 找到w和b的好方法。

正规方程法（Normal Equation):几乎只适用于线性回归，这种方法不需要迭代梯度下降算法，没有推广到其他算法，且当特征数量较大时，正规方程法也很慢（跟线性代数有关，等复习完线代再学）

归一化

特征缩放能够使得梯度下降的速度更快

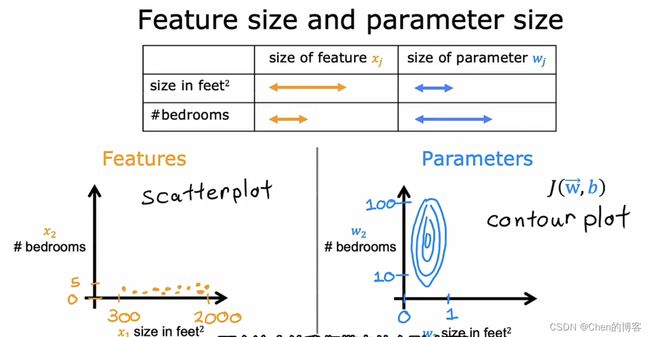
当一个特征的可能值很大时，一个好的模型可能选择一个相对较小的参数值；当特征的可能值很小时，一个好的模型可能选择一个相对较大的参数值。

$$\begin{gathered} 上图为特征散点图和损失函数等高线图 \\ 特征值x_1较大，特征值x_2较小 \\ 好的模型会给x_1一个小参数w_1,给x_2一个大参数w_2 \\ 因为特征值x_1较大，所以w_1的一个小变化会对估计价格\hat{y}产生较大影响，对损失函数J也会产生较大的影响 \\ 而w_2则需要更多的变化才能改变\hat{y}，w_2小的变化几乎不会影响损失函数J \end{gathered}$$

对梯度下降的影响

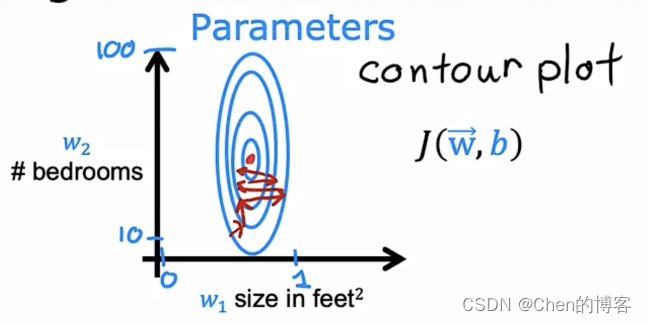
上述参数大小相差很大的情况，会导致损失函数J的等高线呈椭圆型，在梯度下降的过程中，反复横跳，无法收敛或者收敛速度慢。

解决这个问题就要使用归一化，提前处理数据，将数据的范围统一

归一化具体操作

0-1归一化
$$x^{\ast }=\frac{x-x_{min}}{x_{max}-x_{min}}$$
适用在数值比较集中的情况，如果max和min不稳定，很容易使得归一化结果不稳定，使得后续使用效果也不稳定。实际使用中可以用经验常量来替代max和min。

Z—score 标准化
$$\begin{gathered} x^{\ast }=\frac{x-\mu }{\sigma } \\ \mu 、\sigma 为数据集的均值和方差 \\ \mu =\frac{1}{n}\sum _{i=1}^n{x}_i,\sigma =\sqrt{\frac{1}{n}\sum _{i=1}^n(x_i-\mu {)}^2} \end{gathered}$$

判断梯度下降是否收敛

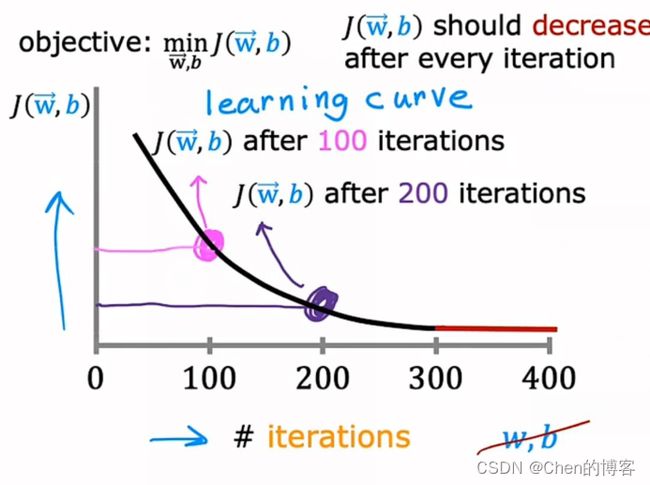
运行梯度下降时，如何判断其是否收敛?

​（损失函数J值与迭代次数图）

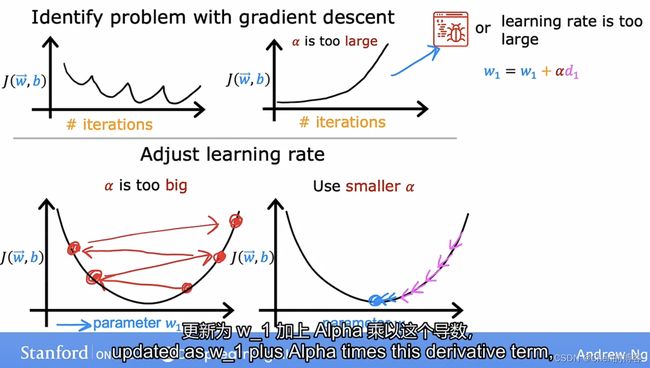
正常情况下，每次迭代损失函数的值都会减少，如果损失函数的值增大了，那么就说明学习率alpha（太大）的值选取不正确，或者代码有问题。

可以通过这个图表来判断收敛，还可以通过下面这种方法来判断是否收敛

自动收敛测试(Automatic convergence test)

$$\begin{gathered} ϵ代表小数的变量，一搬都非常小，例如10^{-3} \\ 如果在一次迭代过程中，损失函数J减小的值小于ϵ，那么损失函数已经到了上图中比较平坦的位置了，那么可以认为已经收敛了 \end{gathered}$$

一般看图是看图判断收敛，容易发现错误。

学习率alpha的选择

学习率太小，程序的运行较慢；学习率太大，可能不会收敛

学习率过大的时候没法收敛，可能出现上图中的情况，上图情况也可能是代码出错。

那么如何选择学习率？

当学习率比较小时，不会出现反复横跳（图像上不会出现损失函数的值随着迭代的次数的增加反而增加的情况）

即每次迭代损失函数J的值都会减少。所以如果梯度下降不起作用，那么就把学习率alpha设置的非常小，如果此时损失函数J任然不会在迭代中减小，或者还会增加，这时候一般就是代码有问题了。

如果学习率alpha非常小，那么就可能经过很多次迭代才收敛，这需要花费很多时间

alpha可以选择：0.001 0.003 0.01 0.03 0.1 1

选择一个小的学习率，再选择一个大的学习率（反复横跳），再尽可能选择大的学习率（收敛），这样做一般可以选择出一个合适的学习率alpha。

逻辑回归(Logistic Regression)

特征工程:使用直觉去设计新的特征，通过变换和组合原始数据
回归算法在解决分类问题时，效果并不是太好

binary alsssification : 二分类问题，预测结果只有两个可能

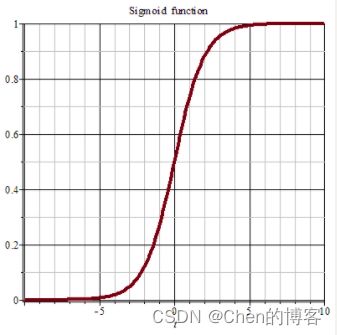
sigmoid/logistic function函数

sigmoid/logistic function函数输出值介于0和1之间
$$\begin{gathered} g(z)=\frac{1}{1+e^{-z}},0<g(z)<1 \\ {f}_{w,b}(x)=z=w\ast x+b \\ g(z)=g(w\ast x+b)=\frac{1}{1+e^{-(w\ast x+b)}} \\ 设置一个阈值，当预测值\hat{y}\ge 阈值时,预测结果为1，当预测值\hat{y}<阈值时,预测结果为0 \\ 常见的阈值=0.5 \end{gathered}$$

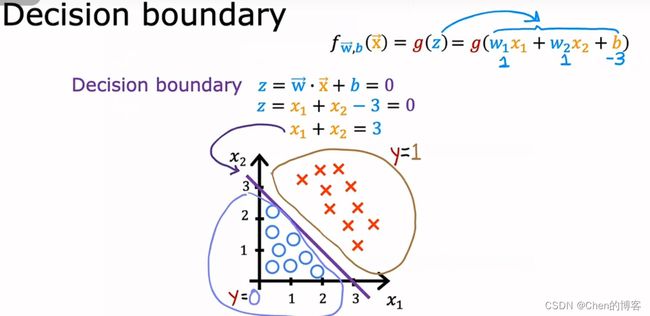
决策边界

KaTeX parse error: Undefined control sequence: \ at position 71: …<3时，\hat{y}=0\ \̲ ̲

非线性的情况：

KaTeX parse error: Undefined control sequence: \ at position 84: …<1时，\hat{y}=0\ \̲ ̲

$$当然还可以构建更加复杂的决策边界,如z=w_1{x}_1+w_2{x}_2+w_3{x}_1^2+w_4{x}_1{x}_2+w_5{x}_2^2，等等$$

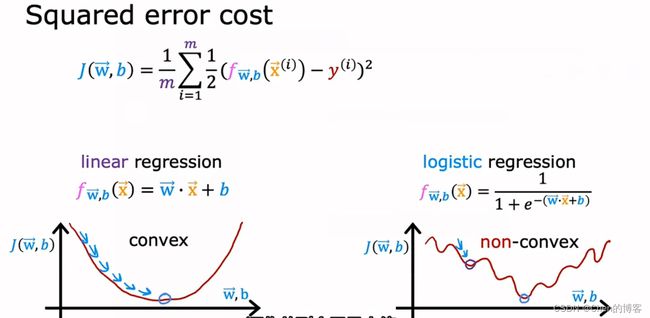
逻辑回归的损失函数

逻辑回归使用线性回归的损失函数，会使得损失函数出现下图的情况，导致梯度下降无法达到最低点

此时损失函数变成非凸函数

定义新的损失函数：
$$\begin{gathered} J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L(f_{w,b}(x^{(i)}),y^{(i)}) \\ L(f_{w,b}(x^{(i)}),y^{(i)})=\{\begin{array}{l}-log(f_{w,b}(x^{(i)}))if{y}^{(i)}=1\\ -log(1-f_{w,b}(x^{(i)}))if{y}^{(i)}=0\end{array} \end{gathered}$$

简化损失函数：
$$\begin{gathered} L(f_{w,b}(x^{(i)}),y^{(i)})=-y^{(i)}log(f_{w,b}(x^{(i)}))-(1-y^{(i)})log(1-f_{w,b}(x^{(i)})) \\ J(w,b)=-\frac{1}{m}\sum _{i=1}^m\left[y^{(i)}log(f_{w,b}(x^{(i)}))+(1-y^{(i)})log(1-f_{w,b}(x^{(i)}))\right] \end{gathered}$$

欠拟合与过拟合

模型对训练集数据的误差称为经验误差，对测试集数据的误差称为泛化误差。模型对训练集以外样本的预测能力就称为模型的泛化能力。

欠拟合

模型的学习能力较弱，而数据的复杂度较高，模型的学习能力较弱，无法从这些复杂的数据中总结出规律，模型在训练集上就表现得很差。

过拟合

模型的学习能力过强，学习了一些没必要的特征，模型过度学习了训练数据，所以模型在训练数据上表现得很好，在测试数据上表现得不好。

造成过拟合的原因一般有：训练样本不足，样本特征少；模型过于复杂。

如何解决过拟合问题

1.获取更多的训练数据

2.看看是否能使用更少的特征来训练模型（会丢失某些信息）

3.正则化，正则化一般缩小特征的参数而不是直接去掉这个特征（参数设置为0），正则化可以保留所有特征，同时防止一些特征产生过大的影响。

正则化

正则化线性回归

$$J(w,b)=\frac{1}{2m}\sum _{i=1}^m(w^{}\ast x^{(i)}+b-y^{(i)}{)}^2+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$

随之改边的梯度下降迭代过程：
$$\begin{gathered} temp\_w_j=w_j-\alpha \frac{\partial }{\partial w_j}J(w,b) \\ 其中,\frac{\partial }{\partial w_j}J(w,b)=\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{w}_j \\ temp\_b=b-\alpha \frac{\partial }{\partial b}J(w,b) \\ 其中,\frac{\partial }{\partial b}J(w,b)=\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)}) \end{gathered}$$

$$\begin{gathered} temp\_w_j=w_j-\alpha \left[\frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{w}_j\right] \\ temp\_w_j=w_j(1-\alpha \frac{\lambda }{m})-\alpha \frac{1}{m}\sum _{i=1}^m(f_{w,b}(x^{(i)})-y^{(i)})x_j^{(i)} \\ (1-\alpha \frac{\lambda }{m})<1,每次迭代收缩w_j一点点 \end{gathered}$$

正则化逻辑回归

$$J(w,b)=-\frac{1}{m}\sum _{i=1}^m\left[y^{(i)}log(f_{w,b}(x^{(i)}))+(1-y^{(i)})log(1-f_{w,b}(x^{(i)}))\right]+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$