一个经典的ROC曲线绘制

一个故事

江湖传闻，ROC曲线最早被用于检测敌军的雷达信号，后来不知怎么的，被应用到心理学，影像学和医学等等。

举个例子，一位医生有两组受试者，一组为正常对照组，一组为病例组，他们的疾病状态分别由目前的金标准所诊断（比如说通过病理活检或临床诊断等等）。同时，这位医生对血液中的某个指标非常感兴趣，想研究这个指标是否可以用于疾病的早期诊断，并且想要评估它的敏感度（Sensitivity）和特异度（Specificity）等参数。最后，想要画出一个ROC曲线帮助更好的评估这项指标的诊断能力。

如果你是这位医生，那你可以这么做。

1. 开始了

# 安装R包
install.packages("pROC")
library(pROC)

2. 加载数据

此例，展示的是pROC包中的示例数据：“aSAH”，其中包含了113例蛛网膜下腔出血患者的临床资料。

> summary(aSAH)
 gos6   outcome      gender        age       wfns       s100b            ndka       
 1:28   Good:72   Male  :42   Min.   :18.0   1:39   Min.   :0.030   Min.   :  3.01  
 2: 0   Poor:41   Female:71   1st Qu.:42.0   2:32   1st Qu.:0.090   1st Qu.:  9.01  
 3:13                         Median :51.0   3: 4   Median :0.140   Median : 12.22  
 4: 6                         Mean   :51.1   4:16   Mean   :0.247   Mean   : 19.66  
 5:66                         3rd Qu.:61.0   5:22   3rd Qu.:0.330   3rd Qu.: 17.30  
                              Max.   :81.0          Max.   :2.070   Max.   :419.19  

为了简化，新建数据集“mydata”，提取其中的三个变量（outcome，ndka和s100b）作为之后统计分析使用。

> mydata <- aSAH[, c("outcome", "ndka", "s100b")]
> summary(mydata)
 outcome        ndka            s100b      
 Good:72   Min.   :  3.01   Min.   :0.030  
 Poor:41   1st Qu.:  9.01   1st Qu.:0.090  
           Median : 12.22   Median :0.140  
           Mean   : 19.66   Mean   :0.247  
           3rd Qu.: 17.30   3rd Qu.:0.330  
           Max.   :419.19   Max.   :2.070 

其中，outcome表示疾病的预后（Good vs Poor），是一个二分类变量。在这个例子中，Good组作为对照组，而Poor组相当于疾病组。ndka和s100b为两个连续变量，是我们感兴趣的研究变量，想要评估它们的诊断能力。

3. ROC图

3.1 来个简单的ROC

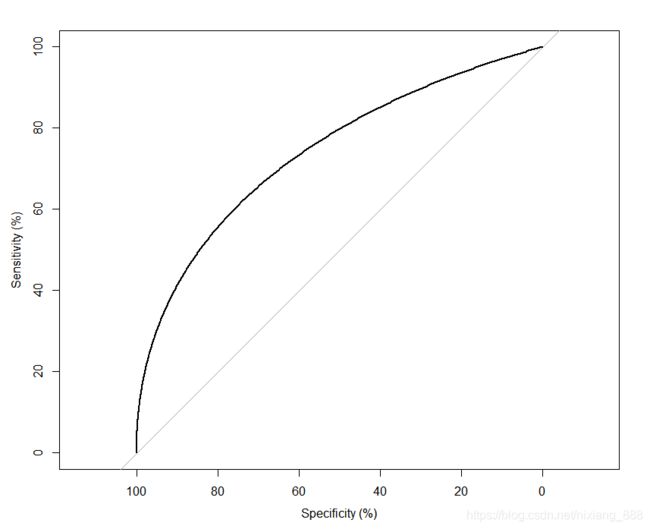
首先，使用outcome（因变量）和s100b（自变量）做一个简单的ROC曲线：

> roc1 <- roc(outcome ~ s100b, smooth = TRUE, percent = TRUE, mydata)
Setting levels: control = Good, case = Poor
Setting direction: controls < cases
> plot(roc1)

代码非常的简单！

不过，上图中有两个重要概念: 敏感度（Sensitivity）和特异度（Specificity），见下图

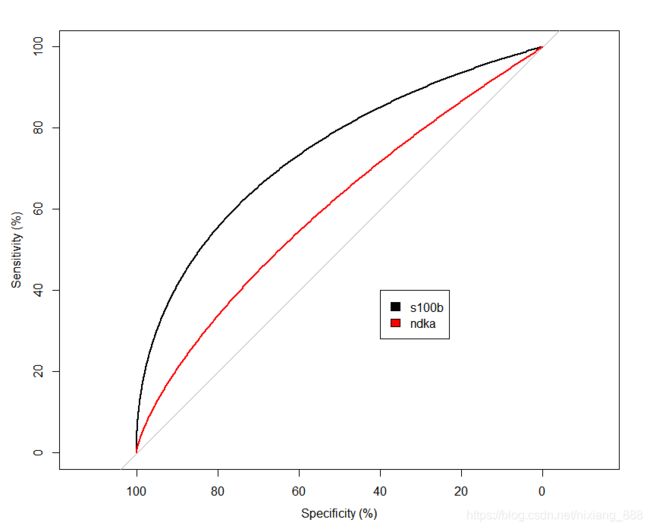
3.2 添加多条

再将ndka的曲线也添加上去，可以这么做：

roc1 <- roc(outcome ~ s100b, smooth = TRUE, percent = TRUE, mydata)
roc2 <- roc(outcome ~ ndka, smooth = TRUE, percent = TRUE, mydata)

plot(roc1)                        # 制作第一条ROC曲线
lines.roc(roc2, col= "red")       # 添加第二条

legend(x = 40, y = 40,            # 添加legend，调整legend的位置
       fill = c("black", "red"), 
       legend = c("s100b", "ndka"),
       cex = 1)

然后再加两条线，共四条，因此这里用到原数据集“aSAH”：

roc1 <- roc(outcome ~ s100b, smooth = TRUE, percent = TRUE, aSAH)
roc2 <- roc(outcome ~ ndka, smooth = TRUE, percent = TRUE, aSAH)
roc3 <- roc(outcome ~ age, smooth = TRUE, percent = TRUE, aSAH)
roc4 <- roc(outcome ~ wfns, smooth = TRUE, percent = TRUE, aSAH)

plot(roc1)                            # 第一条曲线
lines.roc(roc2, col= "red")           # 第二条曲线
lines.roc(roc3, col= "steelblue")     # 第三条曲线   
lines.roc(roc4, col= "goldenrod1")    # 第四条曲线 

legend(x = 30, y = 50, 
       fill = c("black", "red", "steelblue", "goldenrod1"), 
       legend = c("s100b", "ndka", "age", "wfns"),
       cex = 1)

3.3 划重点了：比较两个ROC曲线，统计学显著性

我们做出了s100b和ndka的ROC曲线：

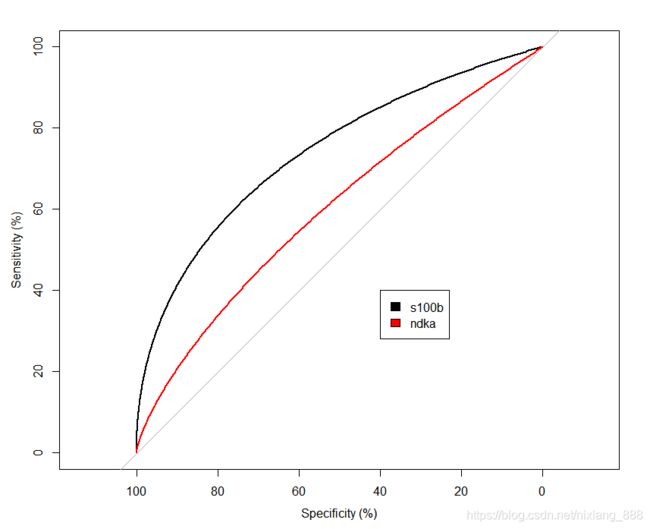
从肉眼上看，s100b的曲线下面积（AUC）要大于ndka，因为黑色线条要高于红色线条。

但它们之间是否真的有统计学意义？回答这个问题可以这么做：

> roc1 <- roc(outcome ~ s100b, smooth = T, data = mydata)
Setting levels: control = Good, case = Poor
Setting direction: controls < cases
> roc2 <- roc(outcome ~ ndka, smooth = T, data = mydata)
Setting levels: control = Good, case = Poor
Setting direction: controls < cases
> roc.test(roc1, roc2, paired = TRUE, method = "bootstrap")   # 使用method = "bootstrap"

	Bootstrap test for two correlated ROC curves

data:  roc1 and roc2
D = 1.6729, boot.n = 2000, boot.stratified = 1, p-value = 0.09434
alternative hypothesis: true difference in AUC is not equal to 0
sample estimates:
Smoothed AUC of roc1 Smoothed AUC of roc2 
           0.7400129            0.6005699 

从输出的结果可知，roc1和roc2的AUC（smoothed AUC，平滑后的曲线下面积）分别为0.74和0.6，但p值为0.098，提示没有统计学上的差异。