机器学习-贝叶斯分类器原理及其sklearn实现

前言

贝叶斯分类器是一种概率模型，它用贝叶斯公式解决分类问题。我们假设样本的特征向量服从某种概率分布，则可以计算特征向量属于每个类的条件概率，条件概率最大的即为分类结果。如果假设特征向量各个分量之间相互独立，即为朴素贝叶斯分类器。如果假设特征向量服从多维正态分布，则为正态贝叶斯。
突然发现有三个公式没有打上去，已修改。

1.贝叶斯决策

条件概率描述了两个有因果关系的随机变量之间的概率关系，p(b|a)定义为在时间a发生为前提下，事件b发生的概率。贝叶斯公式阐明了两个随机事件之间的概率关系：

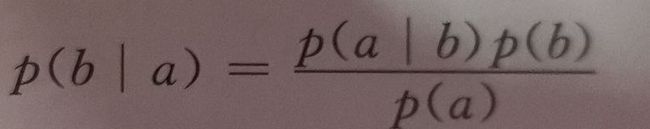
这个结论可以推广到随机变量。分类问题中特征向量的取值x和样本所属类别y具有因果关系。因为样本属于y，才有特征x。比如说一般情况下苹果是红的，因为他是苹果，它才有红色的特征。而我们的分类器要做的相反，是在已知特征向量x的情况下反推样本所属的类别，比如说已知红色水果特征，反推它是苹果这个类别。根据贝叶斯公式：

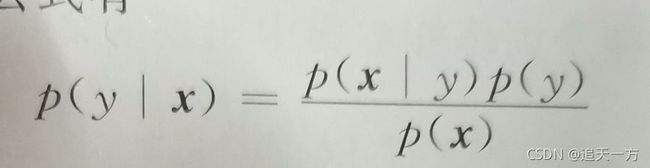
只要知道特征向量的概率分布p(x),每一类出现的概率p(y),以及每一类样本出现的条件概率p(x|y)。就可以计算出样本属于每一类的概率p(y|x)。然后找到最大的那一类即可。p(x)对于每一类的计算都是相同的，因此可以忽略。最终的判别函数为：

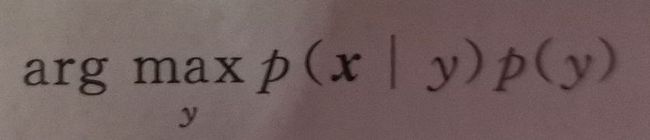
实现贝叶斯分类器需要知道每类样本的特征向量服从的概率分布，现实中很多随机变量都服从正态分布，因此常用正态分布来表示特征向量的概率分布。然后我们使用最大似然估计计算每类样本服从正态分布中的均值和方差两个参数，就能通过计算我们上面判别函数的最终结果，得到分类结果。

2.关于sklearn中的实现

2.1高斯朴素贝叶斯

GaussianNB 实现了运用于分类的高斯朴素贝叶斯算法。特征的可能性(即概率)假设为高斯分布:

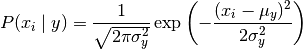
参数均值和和方差使用最大似然法估计。

2.2多项分布朴素贝叶斯

MultinomialNB 实现了服从多项分布数据的朴素贝叶斯算法，参数同样使用最大似然估计计算。

2.3伯努利朴素贝叶斯

BernoulliNB 实现了用于多重伯努利分布数据的朴素贝叶斯训练和分类算法，即有多个特征，但每个特征 都假设是一个二元 (Bernoulli, boolean) 变量。 因此，这类算法要求样本以二元值特征向量表示；如果样本含有其他类型的数据， 一个 BernoulliNB 实例会将其二值化(取决于 binarize 参数)。

伯努利朴素贝叶斯的决策规则基于

与多项分布朴素贝叶斯的规则不同 伯努利朴素贝叶斯明确地惩罚类 y 中没有出现作为预测因子的特征 i ，而多项分布分布朴素贝叶斯只是简单地忽略没出现的特征。

示例

以下使用iris数据集做的一个使用正态朴素贝叶斯分类的代码：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.naive_bayes import GaussianNB
import matplotlib

# 生成所有测试样本点
def make_meshgrid(x, y, h=.02):
    x_min, x_max = x.min() - 1, x.max() + 1
    y_min, y_max = y.min() - 1, y.max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))
    return xx, yy

# 对测试样本进行预测，并显示
def plot_test_results(ax, clf, xx, yy, **params):
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    #画等高线
    ax.contourf(xx, yy, Z, **params)

# 载入iris数据集
iris = datasets.load_iris()
# 只使用前面两个个特征
X = iris.data[:, :2]
# 样本标签值
y = iris.target

# 创建并训练正态朴素贝叶斯分类器
clf = GaussianNB()
clf.fit(X,y)

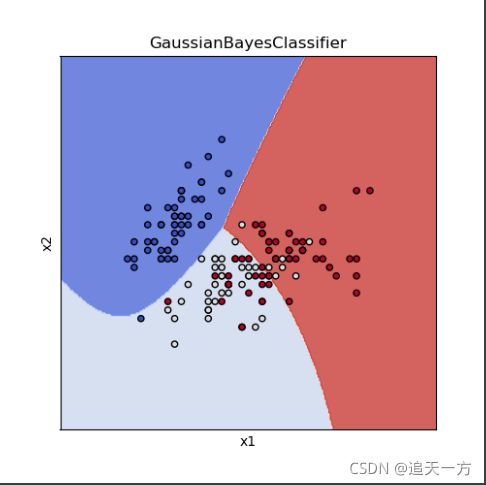
title = ('GaussianBayesClassifier')

fig, ax = plt.subplots(figsize = (5, 5))
plt.subplots_adjust(wspace=0.4, hspace=0.4)

#分别取出两个特征
X0, X1 = X[:, 0], X[:, 1]
# 生成所有测试样本点
xx, yy = make_meshgrid(X0, X1)

# 显示测试样本的分类结果
plot_test_results(ax, clf, xx, yy, cmap=plt.cm.coolwarm, alpha=0.8)
# 显示训练样本
ax.scatter(X0, X1, c=y, cmap=plt.cm.coolwarm, s=20, edgecolors='k')
ax.set_xlim(xx.min(), xx.max())
ax.set_ylim(yy.min(), yy.max())
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_xticks(())
ax.set_yticks(())
ax.set_title(title)
plt.show()

结果如下：