图神经网络与图注意力网络相关知识概述
#图神经网络# #图注意力网络#
随着计算机行业和互联网时代的不断发展与进步,图神经网络已经成为人工智能和大数据的重要研究领域。图神经网络是对相邻节点间信息的传播和聚合的重要技术,可以有效地将深度学习的理念应用于非欧几里德空间的数据上。本期推送围绕图神经网络与图注意力网络相关知识进行概述。
1.什么是图
1.1 定义
图表示的是一系列实体(节点)之间的关系(边)。
- V:节点信息(节点标识、节点邻居数)
- E:边信息(边标识、边权重)
- U:全局信息(节点数、最长路径)
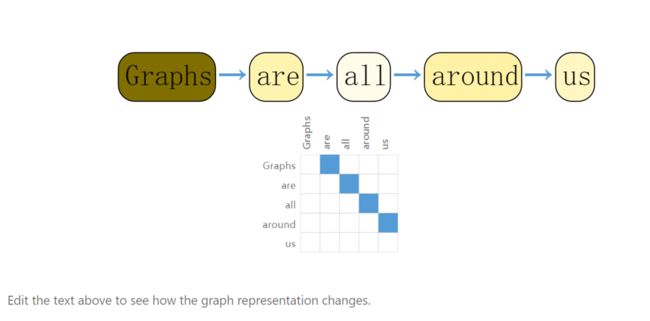
1.2 embedding
为了深入表示每个节点、边和整个图,可以使用如下存储方式:
把节点信息、边信息和全局信息做embedding,通俗说即把这些信息存储为向量的形式。例如上图用向量来表示节点,形成一个长度为6的向量,表示节点的6个信息,高矮代表了值的大小。
1.3 将多种类型的数据表示成图
(1)images as graphs(将图片表示为图)
- 把每个像素作为一个点,存在邻接关系则形成一条边
(2)text as graphs(将文本表示为图)
- 把词表示为顶点,词与词存在有向边
(3)将现实生活中的关系表示成图
- 分子结构(原子之间的关系)、社交网络(人物交互图)、引用(文章引用关系)
- 例如下图为话剧《奥赛罗》中的人物交互图,通过将同时出现在一个场景里的人物连上一条边,将人物关系表示成图。
1.4 在图上面可以定义哪些类型的问题
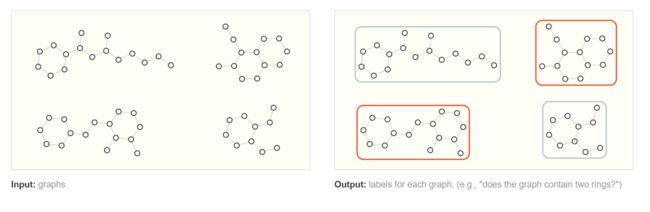
(1) 图层面的任务
- 比如,给定一张图,对该图进行分类。
如上图,预测出哪些分子是具有两个环的。这个例子比较简单,可以用图的遍历来完成,当图非常复杂的时候,图神经网络可以发挥巨大作用。
(2)节点层面的任务
- 比如,将节点分类到不同的阵营。
上图是空手道俱乐部数据集,将学员分类到两个老师的队伍中。
(3)边层面的任务
- 比如,已知节点,学习节点之间的边的信息。
在这个例子中,边的预测是通过语义分割把人物、背景拿出来,然后分析实体间的关系。也就是给出节点之间的图,对边上的属性进行预测。比如黄衣服的人在踢绿衣服的人,他们都站在地毯上。
1.5 在图上使用神经网络的挑战是什么
图上有节点属性、边的属性、全局信息、连接性四种类型的信息。
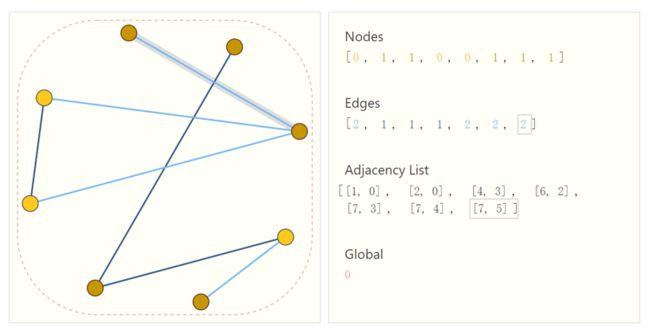
前面三个比较容易与神经网络兼容,因为其可以表示成向量的形式。在利用连接性这种类型的信息时,通常会使用邻接矩阵——但是存在图太大无法存储、交换行列本质不变但矩阵变化的情况。于是很多情况下会使用邻接列表表示图上的连接性关系。
如上图,这张图有8个顶点,7条边。邻接列表的长度与边数相同,第i项表示第i条边连接的哪两个节点。
2.图神经网络
图神经网络的基本思想就是:
- 基于节点的局部邻居信息对节点进行embedding。直观来讲,就是通过神经网络来聚合每个节点及其周围节点的信息。
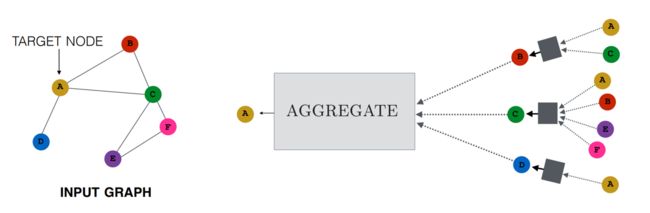
对于这个图来说,要计算节点A的Embedding,有以下的两条想法:
- 节点A的Embedding,是它的邻接节点B、C、D的Embedding传播的结果
- 而节点B、C、D的Embedding,又是由它们各自的邻接节点的Embedding传播的结果。
为了避免无穷无尽,以下图为例,做两层,可以构造该图的传播关系。
第0层即输入层,为每个节点的初始向量,称为初始Embedding。
第1层:
- 节点B的Embedding来自它的邻接点A、C的Embedding的传播。
- 节点C的Embedding来自它的邻接点A、B、E、F的Embedding的传播。
- 节点D的Embedding来自它的邻接点A的Embedding的传播。
第2层:
- 节点A的Embedding来自它的邻接点B、C、D的Embedding的传播。
但是,目前我们还不知道传播到底是什么,图中的小方块在做什么,下面就对传播机制进行介绍。
小方块主要就做了两件事情:
-
收集(Aggregation)
对上一层的所有邻接节点的Embedding,如何进行汇总,获得一个Embedding,供本层进行更新。 -
更新(Update)
对本层已“收集完毕”的邻接点数据,是否添加自身节点的上一层Embedding,如果是,如何添加、如何激活等等,最终输出本层的Embedding。
下面使用公式介绍一个具体例子:
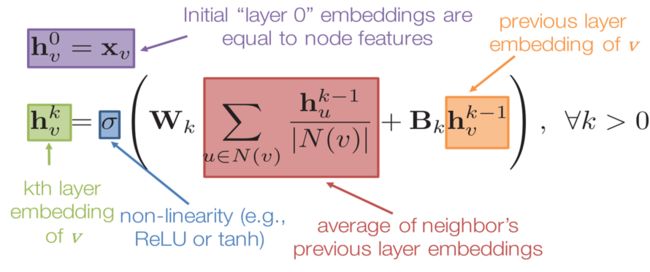
符号解释: h h h表示节点的 e m b e d d i n g embedding embedding,下标 v v v或 u u u表示节点的索引,上标 k k k表示第几层, σ σ σ表示激活函数, W k W_k Wk或 B k B_k Bk表示矩阵, N ( v ) N(v) N(v)表示节点 v v v的邻接点集合。
公式解释:使用节点的输入特征向量来初始化第 0 0 0层节点的 e m b e d d i n g embedding embedding。为了计算第 k k k层节点 v v v的 e m b e d d i n g embedding embedding,需要用到上一层中节点 v v v本身的 e m b e d d i n g embedding embedding、节点 v v v的邻居节点在 k k k-1层中的 e m b e d d i n g embedding embedding平均值。
操作步骤:
- 收集——对上一层邻居节点的Embedding求平均。
- 更新——收集完毕的Embedding与本节点上一层的Embedding进行加权和,然后再激活。
3.图注意力网络
3.1 基本思想
- 根据每个节点在其邻节点上的attention,来对节点表示进行更新。
3.2 改进
- GCN无法允许为邻居中的不同节点指定不同的权重,GAT和GCN的核心区别在于如何收集并累和距离为1的邻居节点的特征表示。
- 图注意力网络GAT用注意力机制替代了GCN中固定的标准化操作。
3.3 优点
- 在GAT中,图中的每个节点可以根据邻节点的特征,为其分配不同的权值。
- 引入注意力机制之后,只与相邻节点有关,即共享边的节点有关,无需得到整张图的信息。
3.4 GAT架构
图注意力层的输入: N N N个节点特征的集合 h h h
h = { h → 1 , h → 2 , . . . , h → N } , h → i ∈ R F h=\{\overrightarrow{h}_1,\overrightarrow{h}_2,...,\overrightarrow{h}_N\},\overrightarrow{h}_i\in\mathbb{R}^F h={h1,h2,...,hN},hi∈RF
图注意力层的输出:经过学习之后的 N N N个节点的特征向量 h ′ h' h′
h ′ = { h → 1 ′ , h → 2 ′ , . . . , h → N ′ } , h → i ′ ∈ R F ′ h'=\{\overrightarrow{h}^{'}_1,\overrightarrow{h}^{'}_2,...,\overrightarrow{h}^{'}_N\},\overrightarrow{h}^{'}_i\in\mathbb{R}^{F'} h′={h1′,h2′,...,hN′},hi′∈RF′
特征增强:为了使得节点特征表达得更清晰,首先对每一个节点进行一个线性变换,即乘上一个权重向量。【 W W W维度为′×,作用:比如将一个长向量转为一个短向量,使得特征更容易提取】
对每个节点实行自注意力机制:注意力系数为
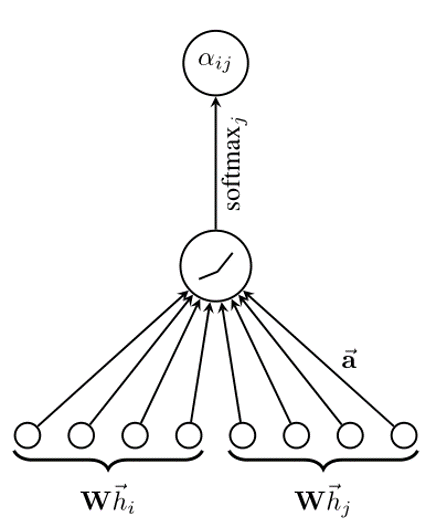
e i j = a ( W h → i , W h → j ) ( 1 ) e_{ij}=a(W\overrightarrow{h}_i,W\overrightarrow{h}_j)(1) eij=a(Whi,Whj)(1)
其中, e i j e_{ij} eij代表节点 j j j的特征对节点 i i i的影响, a a a代表计算两个节点(特征向量)相关度的函数。
本文通过masked attention将图结构加入到机制中,masked attention的含义是:仅将注意力分配到节点i的邻居节点集上(包括i本身)。
α i j = s o f t m a x j ( e i j ) = e x p ( e i j ) ∑ k ∈ N i e x p ( e i k ) ( 2 ) \alpha_{ij}=softmax_j(e_{ij})=\frac{exp(e_{ij})}{\sum_{k\in N_i}exp(e_{ik})}(2) αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)(2)
为了使得注意力系数更容易计算和便于比较,引入了 s o f t m a x softmax softmax对所有的 i i i的相邻节点 j j j进行正则化。
公式2的含义:节点 j j j对 i i i的影响/节点 i i i一阶邻居对 i i i的影响之和。
注: e i j e_{ij} eij和 α i j \alpha_{ij} αij都叫做“注意力系数”,只不过 α i j \alpha_{ij} αij是在 e i j e_{ij} eij基础上进行归一化后的。
将公式1和2进行综合,注意力系数 α i j \alpha_{ij} αij的计算过程即如上图所示: W W W乘上 i i i的特征, W W W乘上 j j j的特征,然后连接起来,乘上权重向量 a a a,形成圈里的值是 e i j e_{ij} eij,再使用 s o f t m a x j softmax_j softmaxj进行归一化,形成新的注意力系数。
通过上述运算得到了归一化后的不同节点之间的注意力系数,可以用来预测每个节点的输出特征:
h → i ′ = σ ( ∑ j ∈ N i α i j W h → j ′ ) ( 3 ) \overrightarrow{h}^{'}_i=\sigma(\sum_{j\in N_i}\alpha_{ij}W\overrightarrow{h}^{'}_j)(3) hi′=σ(j∈Ni∑αijWhj′)(3)
3.5 多头注意力机制
因为多个注意力机制学习到的attention侧重点可能略有不同,所以将K个独立的注意力机制的结果进行级联或者求平均,确保GAT更加稳定。下图展示是K=3的情况,使得结果更加稳定。
4.总结
本期推送从什么是图、图神经网络的基本思想、图注意力网络的基本思想三个方面对图神经网络相关的基础知识进行了介绍。图神经网络从提出发展到现在,针对不同的领域一直在进行改进和优化,已经可以应用到非常多的方面,因为其解决图相关问题的能力强大,所以未来仍有非常大的发展空间,会有更多优秀的模型被提出,解决更加复杂的问题。
5.参考文献
[1] Distill《A Gentle Introduction to Graph Neural Networks》
[2] Hamilton W L, Ying R, Leskovec J. Representation learning on graphs: Methods and applications[J]. arXiv preprint arXiv:1709.05584, 2017.
[3] Velickovic P, Cucurull G, Casanova A, et al. Graph attention networks[J]. stat, 2017, 1050: 20.