李宏毅ML笔记2:回归

P3的主要内容和数学建模的线性回归很像哦, P4有一股概率论与数理统计味儿

公式每次截成图片再一个个插入太麻烦了,打算编辑时候就放word和latex两个版本,哪个能显示看哪个吧.

https://blog.csdn.net/ygdxt/article/details/82288735(这是markdown编辑器的用法)

富文本则是两个$:

https://blog.csdn.net/lzuacm/article/details/81192211?utm_source=blogxgwz9

预览:

https://www.numberempire.com/latexequationeditor.php

https://katex.org/

最后还发现一个在线转换:

https://blog.csdn.net/qq_41251963/article/details/114699612

https://johnmacfarlane.net/texmath

目录

宝可梦研究发布会

1.model

2.函式的好坏

3.最好的函式

更换模型

增加模型幂

其他影响因素

正则化Regularization

error来源

估算过程中的偏差与方差

模型选择

---

宝可梦研究发布会

特点:输出数值Output a scalar

股票预测系统(预测点数), 自动驾驶(方向盘角度),商品推荐(购买可能性值)

预测宝可梦进化后的战斗力(CP Combat Power)

输入:宝可梦x所有信息(属性cp:进化前cp, s:物种, hp:血量, w重量, h高度), 输出:进化后CP

机器学习3步骤: 1.给定model=function set 2.估计function好坏 3.找到最好的function

1.model

给定一个function set,假设y=b+a*cp(ab是任意参数, 则可以由ab组合出无穷多个f, 通过训练数据得到合理的函式)

这种model是linear model:

$$y = b + \sum w_i x_i , x_i: x_{cp}, x_{hp}, x_w,x_h; _: weight, b: bias $$

Input中x的各种数值=feature, w和b不是

2.函式的好坏

通过Training Data可以定义function的好坏

属于监督学习task, Training Data需要input进化前,output进化后两部分组成

用上标表示object编号,下标表示属性编号

定义function的好坏, 用Loss function L

Input: a function, output: how bad it is

L()= L(, ) (因为f由参数wb决定,所以输入f就是输入wb)衡量一组参数的好坏

L一般定义为输出误差的平方: 

$$ L(, ) = \sum_{n=1}^{10} (\hat{y}^n – ( b + w*x_{cp}^n ) )^2 $$

3.最好的函式

从function set中挑选最好的function

线性函式可以通过损失函式找封闭解(closed-form solution)

(如果暴力解,就穷举所有可能值)

不过这里一般用梯度下降法(Gradient Descent):

假设只有1个参数

1. 随机选取初始参数w

2. 计算这个点上L对w的微分

$$ k = \frac {}{} |_{ =^0 } $$

微分=切线斜率>0则左边Loss高,右边Loss低

找Loss低的点, 所以增量与k符号相反, w-=ηk, (步长ηk, η = learning rate, k为斜率)

给定的learning rate决定参数更新的幅度

最后找到的最小值可能是Local minima, 也可能global minima( 不过Linear模型不用担心陷入局部, 因为它是convex凸函数, 只有一个最优解optimal = 全局最优 )

假设有2个参数

梯度的方向也就是等高线的法线方向, 此时梯度gradient为

$$ \nabla L = \begin{bmatrix} \frac {\partial }{\partial } \\ \frac {\partial }{\partial b} \end{bmatrix} $$

 

1. 随机选取初始参数w, b

2. 分别计算这个点上L对w,b的偏微分

$$ k_w = \frac {\partial }{\partial } |_{ =^0 , b=b^0 }, k_b = \frac {\partial }{\partial b} |_{ =^0 , b=b^0 } $$

$$ Δw = -ηk_w, Δb = -ηk_b $$

迭代计算两个偏微分

$$ L(, ) = \sum_{n=1}^{10} (\hat{y}^n – ( b + w*x_{cp}^n ) )^2 \\ \frac {\partial }{\partial } = \sum_{n=1}^{10} 2(\hat{y}^n – ( b + w*x_{cp}^n ) )( -x_{cp}^n ) \\ \frac {\partial }{\partial b} = \sum_{n=1}^{10} 2(\hat{y}^n – ( b + w*x_{cp}^n ) )( -1 ) $$

找到最好的b = -188.4, w = 2.7 (训练集平均误差31.9, 看测试集是35.0)

更换模型

增加模型幂

1次式模型结果怎样

b = -188.4, w = 2.7

Average Error( 这个指标之后一直用来衡量结果好坏 ):

$$ Average\ Error = \frac 1 n\sum_{i=1}^n e^i $$

训练集error=31.9, 测试集error=35.0

更换为2次式作为模型

$$y = b + w_1 * x_{cp} + w_2 * (x_{cp})^2 $$

此时用梯度下降法找到最好的function: b = -10.3, w1 = 1.0, w2 = 0.0027

训练集Average Error = 15.4,测试集Average Error = 18.4

3次式作为模型时,w3已经小到10的-6次方了. 训练集,测试集Average Error都稍好一点

4次式作为模型时,训练集Average Error好一点,但测试集变糟糕了

5次式模型拟合出来已经很明显反逻辑了,测试集没法看了

 

5次式模型是包含4次式模型的(只需把w4设为0), 所以理论上来说,它选择更多,可以找到训练集误差更小的function. 但是在测试集上表现完全不同

其他影响因素

当有更大的数据集出现, 明显分布不是单一因素的幂函数. 宝可梦的物种产生非常关键的影响.

回到第一步, 重新设计model( function set ),考虑输入x与输出y关系

可以不同的物种代入不同的参数

$$ _ = species \ of \ x \\ If\ _ = ``Caterpie": = _3 + _3 * _{} \\ If\ _ = ``Eevee": = _4 + _4 * _{}  $$

含有if还可以当作linear model算微分吗?

可以通过改写( 哦哟这个好像数学建模中的0-1变量 ):

$$ \begin{equation}          \delta ( _ = Pidgey ) =        \begin{cases}               1 & if\ _ = Pidgey\\               0 & otherwise        \end{cases} \end{equation} \\ y = \delta ( _ = Pidgey ) * ( b_1 + w_1 * x_{cp} )+\\ \ \delta ( _ = Eevee ) * ( b_2 + w_2 * x_{cp} ) \\ … $$

还是linear model的形式:

$$y = b + \sum w_i x_i $$

测试集可以得到更小的误差: 14.3

还有没有其他可能的参数呢?

重量/高度/HP, 没有领域知识不能判断,把能想到的参数和平方都塞进去弄个最复杂的function, 结果又过拟合了(训练集误差很低, 测试集误差很高)

正则化Regularization

重新定义损失函式.

原来的损失函式只考虑了预测的误差, 加一项考虑w大小(∑(_ )^2),但不用考虑bias, bias与平滑程度无关.

$$ L = \sum_{n} ( \hat{y}^n – ( b + w*x_{cp}^n ) )^2 + \lambda \sum ( w_i )^2 $$

期待参数的值更小的function, 意味着更平滑, 输出受输入影响更小, 当测试集的输入含噪声时, 平滑的函式受更小的影响.

$$ y + \sum w_i \Delta x_i = b + \sum w_i ( x_i + \Delta x_i ) $$

λ越高越平滑, 在训练集上得到的误差越大,但是在测试集上先减小后增加

通过调整λ决定平滑程度

error来源

通过训练集估算得到函式h并不会真的等于真实f

如果可以诊断error的来源, 就可以改进model

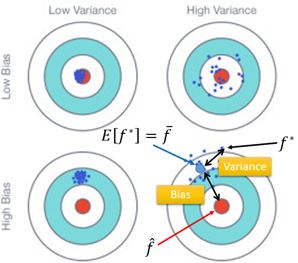
error来自什么地方: 1.bias 2.variance

估算过程中的偏差与方差

设x的真实(总体)均值μ,真实方差σ^2

估算均值为m

根据n个样本估算变量x的均值为m, m表示的是数理统计中常用的:

$$ m = \bar X $$

样本均值m不等于总体均值μ,除非有无穷多样本

$$ m = \frac{1}{N}{\sum_{i=1}^n x^{i}} $$

但是对m取期望可以得到μ

$$ E(m) = E( {\frac{1}{N}{\sum_{i=1}^n x^{i}}} ) = \frac{1}{N}{\sum_{i=1}^n{E(x^{i})}} = \mu $$

其中最后一步用到样本与总体同分布

$$ E( x^i ) = E(X) $$

样本均值m的方差取决于样本个数:

$$ Var(m)=D(\bar X)= \frac 1 n D(X) = \frac{\sigma^2}{N} $$

上式说明, 只取比较小的N时,不同样本的m会分散的比较开

该式第二个等号的证明:

$$ D\bar X=D(\frac 1 n \sum x_i)=\frac 1 {n^2} \sum Dx_i=\frac 1 {n^2} \sum DX=\frac 1 n D(X) = \frac n{n^2} DX $$

估算方差

根据n个样本估算变量x的方差

先用刚刚的方法估测m,再计算xi与m的方差

$$ s^{2} = \frac{1}{N}{\sum_{i=1}^n\left( {x^i - m} \right)^2} $$

s^2与σ^2的分布并非一样, 取s^2的期望值, 会比σ^2小一点

$$ E(s^{2}) = \frac{N - 1}{N}\sigma^{2} \neq \sigma^{2} $$

N越大,对方差的估测误差就越小

那怎么知道估算是不是有bias?

对所有h取期望, 看是否与f期望一样

要取很多个h, 需要多次实验, 用同样的model,但给的data不一样, 找到的h也不一样

用简单的model

得到的h线比较集中(受样本数据影响更小, 方差小),

但E(h) 与真实f比较的bias较大(可能function set中根本没有包含target目标函式)

复杂的model

散布就很广(受样本数据影响更大, 方差大)

但E(h) 与真实f比较的bias较小

从简单到复杂,模型的bias造成的误差逐渐下降,模型的variance造成的误差越来越大

underfitting

误差主要来源于bias, 模型在训练集表现不好

改进: 需要重新设计model,加入更多feature(更多训练数据也不会有帮助)

overfitting

误差主要来源于variance时, 模型在训练集表现好, 在测试集表现不好

改进:

1.增加data(是很有效控制variance的方法)

2.正则化(regularization), 损失函式加入一项控制参数更小,曲线更平滑(但有可能伤害bias)

模型选择

需要在bias与variance之间权衡

通过训练集训练出的f,如果在测试集上误差最小, 不一定在真实数据上误差最小. (测试集也可能有bias)

那可以从训练集中拿一点出来当验证集, 用来选model. (选好之后可以拿训练集+验证集一起训练一下)

如果不相信分出来的validation, 一次训练-测试的结果, 觉得也有bias. 也可以做交叉验证,

N-fold Cross Validation:

把训练集分成三份, 每一份轮流充当验证集得到误差. 最后选择平均误差最小的模型

原则是不要根据测试集调整模型