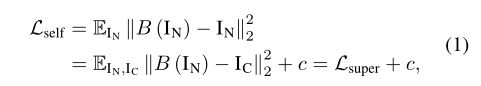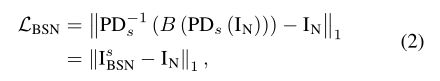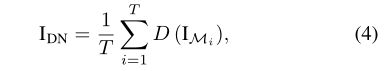AP-BSN: Self-Supervised Denoising for Real-World Imagesvia Asymmetric PD and Blind-Spot Network

个人论文阅读笔记，可能存在许多瑕疵和错误，欢迎评论指正，谢谢~~

1. 总括

盲点网络BSN假设噪声信号是像素独立且零均值的情况下，从相邻噪声像素重建干净像素而不参考相应的输入像素。然而已知真实噪声（图像上存在的真实噪声，并非合成噪声）具有空间相关性，这不符合BSN的基本假设：噪声与像素无关。

由于像素独立于噪声等不太实际的假设，使用自监督盲点去噪网络处理空间相关的真实噪声具有挑战性。为了打破真实噪声的空间相关性，PD通过使用固定步长因子对噪声图像进行了下采样来创建马赛克 ，从而增加噪声信号之间的实际距离。然而，当以完全自我监督的方式处理真实噪声时，将PD集成BSN并非易事，如果没有来自额外的噪声清洁合成对的知识，它就无法独立存在。造成这种限制的主要原因是像素独立假设和重建质量之间的权衡。例如，较大的PD步长因子（＞3）可以确保严格的像素独立噪声假设，并有利于训练期间的BSN。然而，它也会破坏噪声图像中的详细结构和纹理。相反，较小的PD步长因子（＜3）在训练BSN时，保留了图像结构，但不能满足像素独立假设。

受这些观察结果的启发，本文提出了非对称PD（AP），它使用不同的步幅因子进行训练和推理。对于真实噪声，我们系统地验证了训练和推理步长的特定组合可以弥补彼此的缺点。然后，将AP集成到BSN（AP-BSN），它可以学习以完全自我监督的方式去噪真实噪声输入，而不需要任何潜在噪声的先验知识。所提出的AP可以解决特定PD步长因子引起的固有权衡，并使用BSN适用于实际场景。此外，提出了随机替换细化（），这是一种新的后处理方法，可以不增加任何额外训练（任何参数）的的情况下提高AP-BSN的性能。

2. BSN and PD

2.1. Blind-spot network.

BSN是传统CNN的变体，它没有看到感受野的中心像素来预测相应的输出像素。BSN 可以学习以自监督的方式对噪声图像进行去噪。为了简单起见省略了颜色通道,所以图像的分辨率为H×W。要训练BSN，必须满足以下两个假设：噪声时空间上的，既像素级的、独立的和零均值的。在这样的假设下，最小化自监督损失等价于传统的监督学习，如下所示：

其中是噪声输入的干净真实值，是监督去噪损失函数，c是常数。

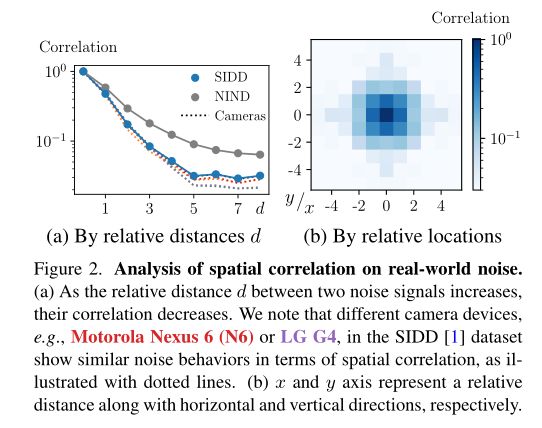
图2表示，在现实世界中，相邻像素之间的噪声强度基于其相对距离显示出不可忽略的相关性。由于相邻的噪声信号可以作为推断看不见的中心像素的线索，我们已经确定BSN在真实的sRGB图像上作为近似恒等映射。

2.2. Pixel-shuffle downsampling 

PD被用于打破真实噪声中的空间相关性。具体来说，被视为步长因子为s像素重组的逆操作。由于真实噪声信号与少数相邻像素有关，PD过程中的下采样可能会打破它们之间的依赖关系。然后传统的去噪算法可以应用于降采样图像，其中PD逆运算之后重建全尺寸输出。为了保留图像纹理和细节，将步长因子设置为2，即，以获得最佳性能。

PD原文关于PD的解释：Pixel-shuffle Down-sampling被定义为通过以步幅 s 对图像进行采样来创建马赛克。与线性插值、双三次插值和像素面积关系等其他下采样方法相比，对噪声图像进行Pixel-shuffle和最近邻下采样不会影响真实的噪声分布。此外，与其他像素相比，Pixel-shuffle还可以通过保留图像中的原始像素来促进图像恢复。这两个优势产生了 PD 策略的两个阶段：适应和细化 

3. Method

我们的目标是以自监督的方式在真实的sRGB图像上推广BSN，为此，我们采用PD并最小化以下损失来训练BSN：

其中，是和BSN的管道的输出，即。我们使用范数来更好地泛化，而不是损失。首先将给定的噪声图像分解为子图像。是这些子图像的平铺，如图4所示。然后，我们将BSN应用于子图像，并使用PD逆运算重建输出。

当使用等式（2）中的自监督损失进行训练时，PD-BSN不适用于真实噪声图像。图像3c和3d表明and无法从给定的噪声输入中恢复干净清晰的图像，无论PD步长因子是多少。

3.1. PD-BSN中的权衡

3.1.1. Breaking spatial correlation

最初，PD被提出用于减少真实图像中相邻噪声信号直接的空间相关性。虽然zhou等人采用步长因子2，但我们在图像2a中的分析表明，步长因子应至少为5，以最小化给定噪声信号中的相关性。换句话说，子图像的噪声信号仍然是空间上相关的。其中，BSN的像素独立噪声假设不成立。

3.1.2. Aliasing artifacts(混叠效应)

随着步长因子s变得更大，来自的子图像遭受更强的混叠程度。从信号处理的角度来看，当原始信号没有适当的带宽限制时，降采样会出现混叠。由于PD过程在子采样之前不利于低通滤波器，我们已经确定，当应用大跨距PD时，混叠作为一种噪声形式发生，例如s＝5，如图4所示。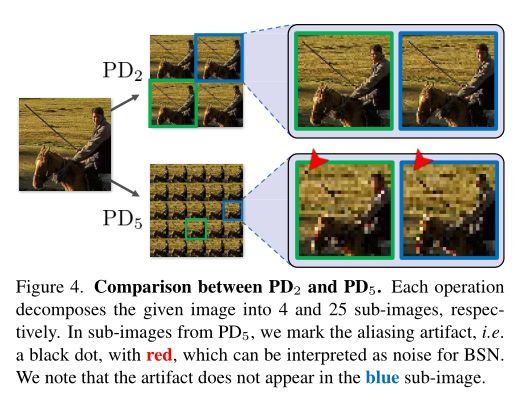

和之间的比较。每个操作分别将给定图像分解为 4 和 25 个子图像。在来自 PD5 的子图像中，我们用红色标记了混叠伪影，即黑点，这可以解释为 BSN 的噪声。且该伪影没有出现在蓝色子图像中。 

3.2. Effective training stride factor for PD-BSN

我们建立了一个训练的策略，为此，必须最小化训练输入图像中噪声信号之间的相关性。然而，如第3.1节所述，不足以打破真实世界噪声的空间相关性。由于不满足BSN的基本假设，该模型无法学习使用进行去噪。通过设置s＝5来抑制训练样本中噪声信号之间的空间相关性，我们可以在较小的子图像上训练BSN。

我们注意到，BSN还学习了消除由大PD步长因子引起的混叠效应。当在下采样之前未移除高频信号时，就会发生混叠。由于原始噪声图像中的高分辨率分量变化迅速，我们可以忽略子图像中混叠效应的空间相关性。效应也满足零均值约束，即其统计均值与中噪声图像的统计均值大致相同，因为它们是观察信号的随机样本，由于混叠效应满足BSN的两个先决条件，PD-BSN也学会了删除它们。

3.3. Asymmetric PD for BSN

一些研究已经确定，训练样本和测试样本之间的匹配数据分布在准确的图像去噪中起着关键作用。在应用PD-BSN时，自然可以使用相同的步长因子进行训练和推理。然而，我们发现学习的BSN将来自的混叠伪影识别为噪声信号，以便在推理过程中去除。由于这些伪影包含重建高频细节的必要信息，在推理过程中破坏图像结构，同时去除噪声。 

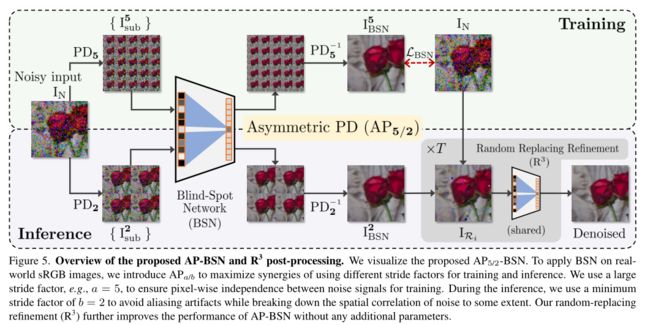
相反，我们在PD-BSN的推理过程中提出了一个非对称步长因子，我们称之为非对称。a和b分别是训练和推理的步长因子。设置b＝2，以便子图像在推理期间包含最小的混叠伪影，同时可以降低相邻噪声信号之间的相关性。我们的BSN和拟议的可以学习以自我监督的方式去除真实世界的噪声，同时保留图像结构。AP-BSN不需要任何干净的样本进行训练，并且在实际场景中直接适用于sRGB噪声图像。图5说明了我们针对AP-BSN的非对称训练和推理方案。

 

拟议的 AP-BSN 和  后处理概述。我们可视化提出的 。为了将 BSN 应用于真实 sRGB 图像，我们引入了 以最大化使用不同的步幅因子进行训练和推理的协同作用。使用较大的步幅因子，例如 a = 5，以确保训练噪声信号之间的像素独立性。在推理过程中，使用最小步幅因子 b = 2 来避免混叠伪影，同时在一定程度上打破噪声的空间相关性。我们的随机替换细化 () 进一步提高了 AP-BSN 的性能，无需任何额外参数 。

3.4. Random-replacing refinement

即使步长因子最小，PD和后续去噪步骤也可能会从输入中删除一些信息丰富的高频成分，从而产生视觉伪影。因此，zhou等人提出来了PD细化。以抑制PD过程中的伪影，并增强去噪结果的细节。PD细化，第i个替换图像公式如下：

其中是个二进制掩膜，指示要替换的像素，并且表示元素相乘。在这里，是一个结构化的二进制矩阵，其中以2的固定步长放置，并且。替换后，再次对每个图像进行去噪并取平均值，以重建最终结果，如下所示：

 

其中D是针对像素独立噪声的去噪模型，T是原始PD细化的掩码数。

然而，PD细化中确定性策略在被替换的噪声信号之间留下了不可忽略的相关性。具体而言，如图6a所示，中被替换的噪声像素始终与其一些邻居相关。这种相关性会对以下去噪方法D的性能产生负面影响，该方法假设存在空间不相关噪声。因此我们提出一种先进的随机替换细化（）策略来缓解PD细化的局限性。

PD-refinement 和我们的 之间的比较。虽然 PD-refinement 采用步长为 2 的常规二进制掩码 ，但我们的 使用随机掩码  。 在图(a) 中比较了替换图像 和中噪声信号的预期空间相关性。 (b) 每个灰色框代表原始噪声图像 中的一个像素，它替换了 中的去噪像素

在我们的中，我们采用T随机化二进制掩膜，其定义如下： 

其中（x，y）表示H×W矩阵中元素的索引。对于等式（3）和等式（4），我们采用随机掩膜，而不是固定的来获得最终输出。由于噪声像素随机放置在第i个替换图像中，因此两个噪声信号之间的预期相关性乘以p，如图6a所示。因此，与之前的PD细化相比 ，我们的显著降低了预期相关性。当我们将和AP-BSN相结合时，我们不执行PD，而是直接将替换后的图像馈送给BSN，因为输入中噪声的空间相关性几乎可以忽略不计。图6突出了PD细化和我们之间的主要差异。

 完结~~