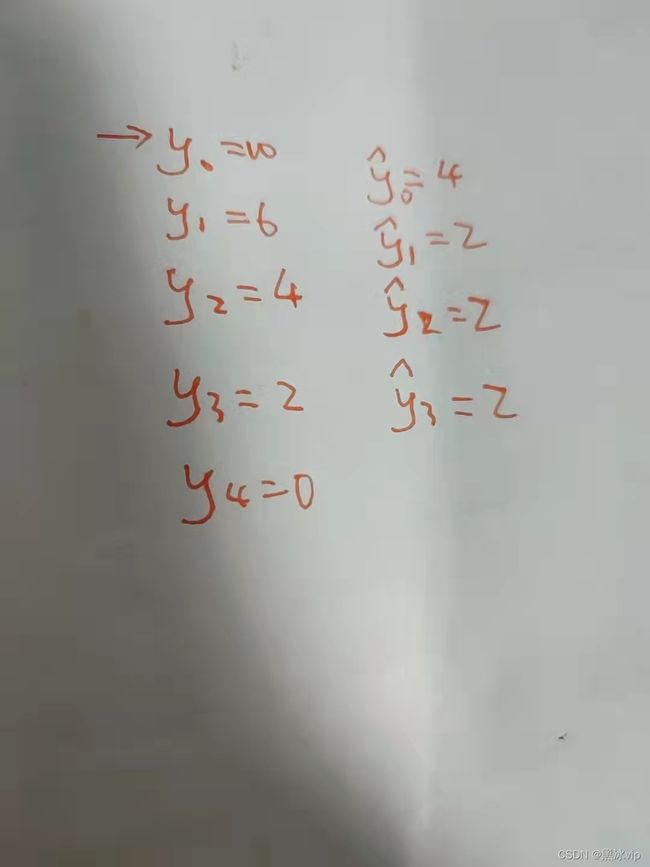4、集成学习:随机森林、Adaboost、GBDT
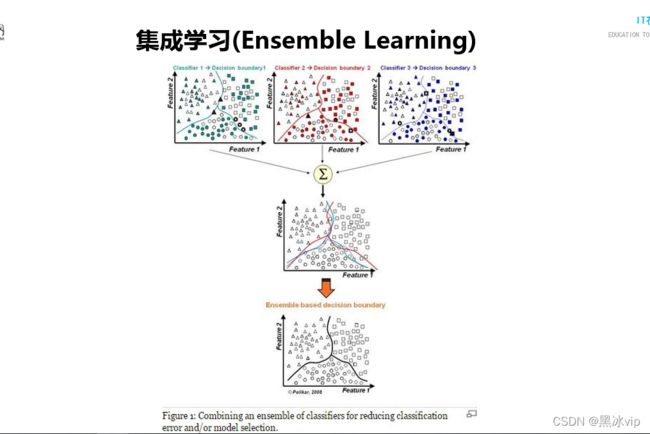
01_集成学习(Ensemble Learning)思想讲解
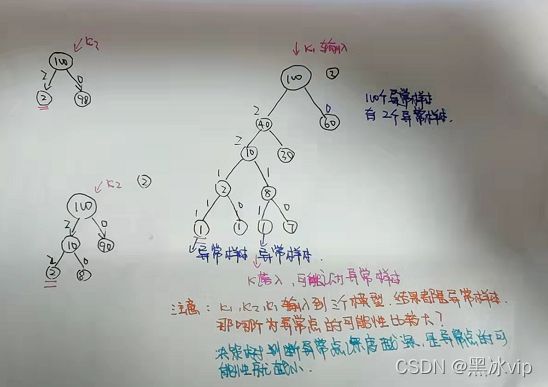
注意:通过若干个学习器组合新的学习器 ,如果有错误样本(鲁棒性不高的模型)也能弱化 (因为正确性居多)
2.数据集过大,不会一次性放入数据集,可以进行拆分
数据集过小,通过有放回操作产生不同的子集
3.有时候模型边界比较复杂,如下图;这时候需要训练多个线性模型,然后将这几个线性模型做一个融合,
最后得到一个非线性的能力
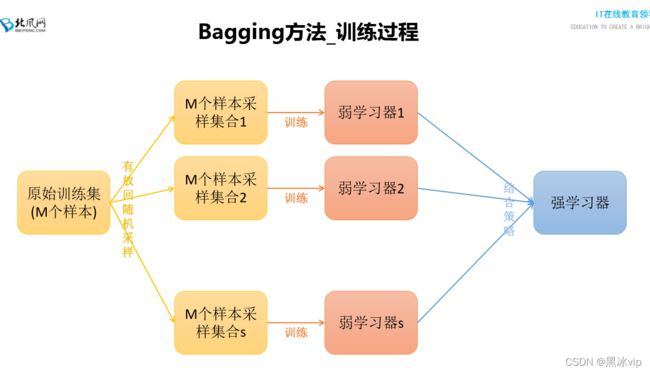
注意:集成学习和深度学习有一定的共通性,深度学习可以当做是多个线性模型(逻辑回归)的融合02_Bagging集成算法思想讲解 
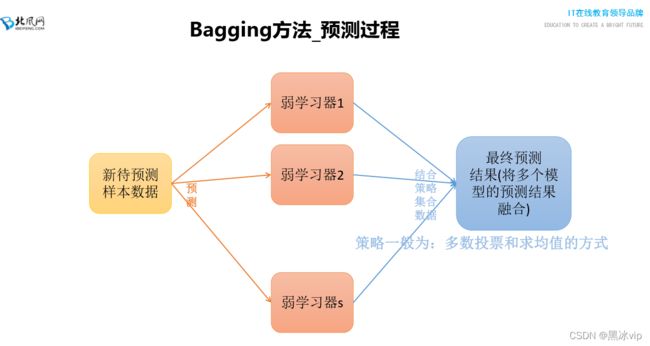
注意:通过多数投票或者求均值的方式来统计最终的分类结果
注意:多数投票->加权的多数投票03_RandomForest集成算法思想讲解
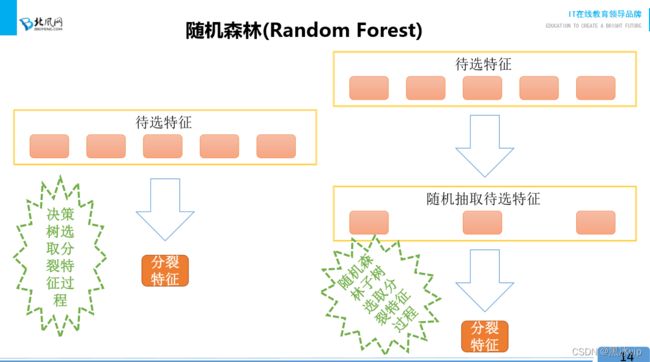
注意:随机森林是对Bagging集成算法稍微做了一点修正区别:决策树从所有的特征中选择最优的那一个
随机森林随机选择特征,然后从选择的特征中选择最优的一个(原因:有效的避免异常样本所在的
类别进行划分)
** 38:00-41:00 讲解异常样本当做一个类别对结果的影响
注意:
1.决策树选择的是最优的特征属性(top1),让叶子节点足够纯
2.随机森林选择的是相对比较优秀的属性(比如top6),但是随机森林的思想就是将多个"弱模型"合并
成强模型
3.所谓的最优不一定就是最优,只是在训练集上最优
决策树解决过拟合方案:
1、剪枝
2、随机森林
2.1 Bagging集成算法思想,构建多个模型(不同数据集),不同数据集找出的划分特征也不一样
(有的考虑颜色,有的考虑大小...),然后各个数据集一融合强弱就做了抵消,从而防止过拟合
2.2 划分特征不是选择最优(注意:最优的概念是训练集),通过随机的过程(随机森林)降低最优
的特性04_RandomForest变种算法讲解
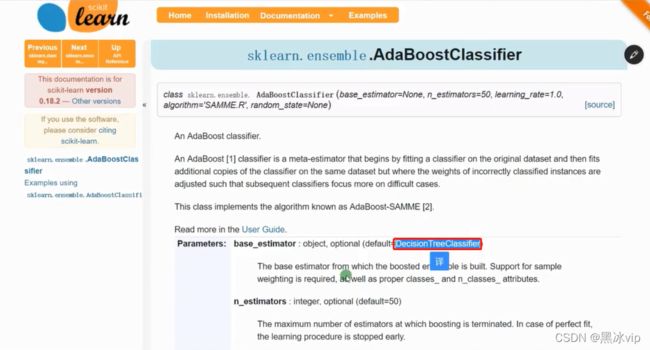
*注意:RandomForest变种算法了解即可,实际开发中用的比较少4.1 Extra Tree
注意:Extra tree实际开发中一般不用,除非发现随机森林效果不好才会使用;(一般不用,作为最后一个
考虑项)
**55:00-56:00 介绍api
**01:01 介绍api
注意:
1、采用相同的数据集
2、与传统决策树不同不是基于信息增益、信息增益率、基尼系数、均方差来选择最优特征值;
Extra Tree随机选择一个特征值来划分决策树(因为数据集相同,划分特征也相同各个模型就
没有效果了;各个模型间的关联性也不会很强)
Extra Tree由于不是使用最优的特征属性去划分,导致分层比较深方差比随机森林小,泛化能力比
RF的强** - 1:17 简介TRTE
注意:将异常样本和正常样本都找出来,然后让异常样本学习正常样本特征,如果符合就说明是正常样本
,不符合就是异常样本
1、因为是异常点检测,数据量不需要很大(很小一部分就可以构建)
3、比如100万样本只有0.001的异常样本,所以样本量不需要那么大比如取1000个,中间大约有1
-10个异常样本(层次也不用太深)
特点:1、数据量少 2、特征随机划分 3、层次不深注意:
3、给特征值做个排序做特征选择
4、随机抽样不会出现偏差比较大的数据,因为异常点都中和了
5、RF直接将机器学习拿过来用,所以实现简单
6、如果特征确失,就会划分为新的分支
1、噪音点确实比较大可以尝试一下Extra tree看看效果
2、特征上的取值比较多,特征划分的话就可能会过多考虑这个特征05_案例代码:随机森林、Bagging算法应用案例讲解
06_案例代码:乳腺癌诊断应用案例代码讲解
**01:39- 02:39 讲解代码
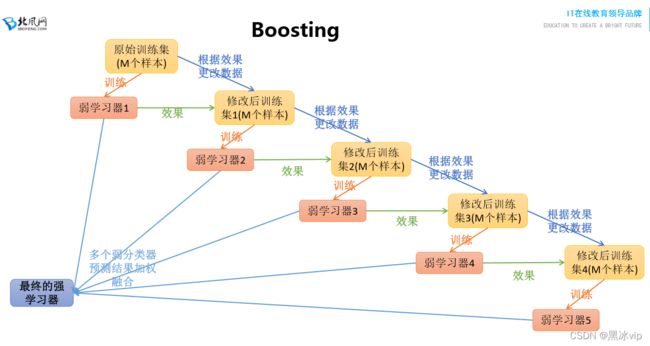
07_Boosting集成算法思想讲解
注意:
1、构建第m棵子树的时候,考虑前m-1棵.例如:只考虑预测错误的数据,预测正确的数据就不考虑了。
这样预测的数据就会更准确,会比随机森林更准确。
2、注意:是对模型结果进行融合,不是对模型参数进行融合
Boosting集成算法与Bagging集成算法区别:
模型样本不一样:Boosting集成算法的样本是一样的,每次取得特征不一样
Bagging集成算法是每次样本不一样(有放回去重)
集成学习的意思:
通过多个弱学习器的融合得到一个强学习器,从而提升模型性能
##02:48-04:07: 03;15- 04:07
08_Adaboost算法原理讲解
如果做回归直接用1公式
如果做分类直接用2公式
注意:第k-1次预测错误,权重加大,第k次继续分错的话,损失函数就会变得大(乘以权重)作为惩罚
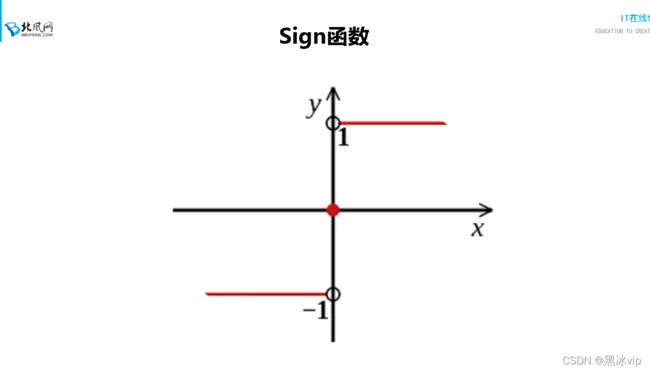
Adaboost算法默认是做二分类
大于0认为是1
小于0认为是-1
等于0选择第一个类别(哪个类别在前就选择哪个类别) ![]() : 第m个模型第i个样本
: 第m个模型第i个样本![]()
09_Adaboost算法模型构建流程讲解_转
10、[20180701]_10_案例代码:Adaboost案例代码讲解_转
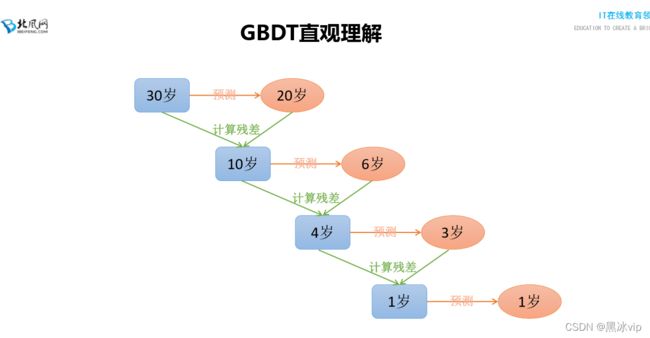
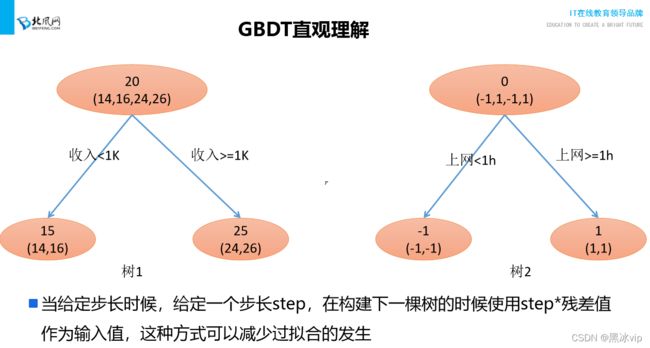
11、[20180701]_11_GBDT算法原理讲解
注意:GDBT工作中用的比较少,用的比较多是XGBoost
原因:GDBT容易陷于过拟合,XGBoost相对性能会好点(XGBoost迭代速度也比GDBT快)GDBT和AdaBoost的区别:
1、GDBT只能是决策树,不支持其他的算法(如上图:AdaBoost算法底层可以不是决策树)
2、GDBT更新方向是让样本的误差尽可能的小(误差变小不是通过更改权重值,是基于梯度去实现的)
注意:所有GDBT算法是回归树(通过Sigmoid函数将回归问题转化为分类问题)##4:13-4:35
12_集成算法之Bagging和Boosting比较总结讲解
**04:36 - 讲解比较总结
**04:43 讲解缩放因子
1、样本选择:
1.1 Boosting改变的是权重的大小,Bagging改变的y的值(y=实际值-预测值 为0说明模型预测准确
用的梯度下降--最小二乘法)
1.2 不管是更新权重还是y值,都是根据上一轮的结果(权重有公式更新,y值有最小二乘法更新 )
2、样例权重
样例为什么是等权重?因为每次随机抽取样本后,还有去重操作,所以样本是等权重
GDBT、Boosting算法中模型都是等权重;Adaboost算法不是等权重;
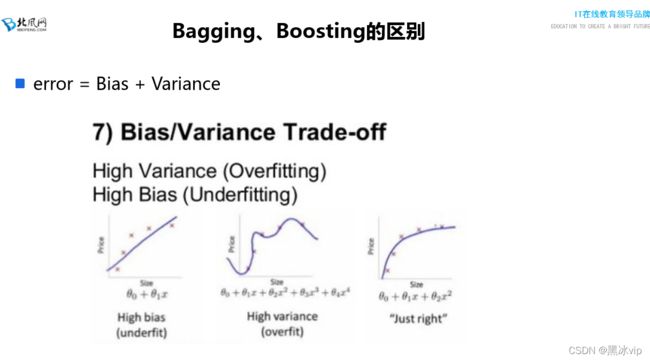
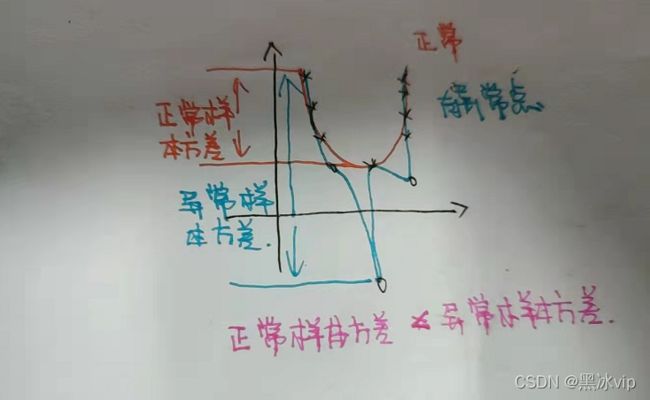
5、 Bias:真实值和预测值之间的偏差(说明样本欠拟合)
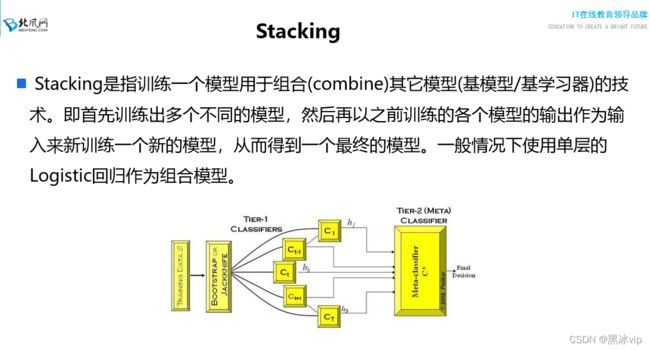
Variance:由于异常点样本方差比正常样本大(说明过拟合)13_Stacking集成算法思想讲解
注意: bagging算法是通过有放回的重采样,每个模型的训练集和测试集不一样;导致每个模型不一样
融合后可以考虑各个模型的方面;
Boosting算法更改样本和实例的权重或者改变y值来构建模型