【ECCV 2022】在目标检测中是否应该平等对待所有proposal?
作者|小马 编辑|3D视觉开发者社区
本篇分享 ECCV 2022 论文『Should All Proposals be Treated Equally in Object Detection?』,微软&UCSD利用动态网络的思想处理不同的proposal,达到更好的检测效率!
详细信息如下:
论文地址:https://arxiv.org/abs/2207.03520
代码地址:https://github.com/liyunsheng13/dpp
1. 摘要
对于资源受限的视觉任务,目标检测器的复杂度-精度权衡是一个关键问题。以前的工作重点是使用高效主干实现检测器。本文研究了检测头处理proposal对这种权衡的影响。
作者认为,提高检测效率需要范式转换,转向对proposal的不平等处理,将更多的计算分配给好的proposal而不是差的proposal。这可以更好地利用可用的计算预算,使相同的浮点运算具有更高的精度。作者将其表述为一个学习问题,其目标是在检测头中为proposal分配算子,从而限制总计算成本并最大限度地提高精度。
关键发现是,这种匹配可以作为一个函数来学习,该函数将嵌入的每个proposal映射到一个one-hot编码中。虽然该功能产生了复杂的动态网络路由机制,但它可以通过简单的MLP和使用现成目标检测器的端到端学习来实现。在给定的计算复杂度下,这种动态proposal处理(DPP)的性能明显优于最先进的端到端目标检测器(DETR、Sparse R-CNN)。
2. Motivation
目标检测是计算机视觉中的一项具有挑战性但基本的任务,其目的是预测图像中每个对象实例的边界框和类别标签。由Faster RCNN 引入的一种流行策略是依靠骨干网来产生相对较大的对象proposal集,并使用检测头从这些proposal中得出最终预测。从那时起,这种两阶段检测框架的设计趋势。最近的方法,如Sparse R-CNN,成功地减少了Faster RCNN的数千个proposal到几百个。
然而,由于使用更复杂的体系结构大大增加了检测头的proposal计算,因此减少proposal数量的总体计算效益是有限的。虽然聚合效应使检测器更高效,但总的来说,这些方法仍然不适合用于较轻的主干,因为检测头复杂度在整体计算中占较大比例。
虽然有效的目标检测现在是计算机视觉中一个广泛研究的问题,但本文主要关注计算效率高的主干的设计。重型检测头的引入将逆转轻量级模型实现的计算增益。例如,具有300个proposal的Sparse RCNN的检测头消耗了整个MobileNetV2 的4倍计算 (25 GFLOPS vs 5.5 GFLOPS)。
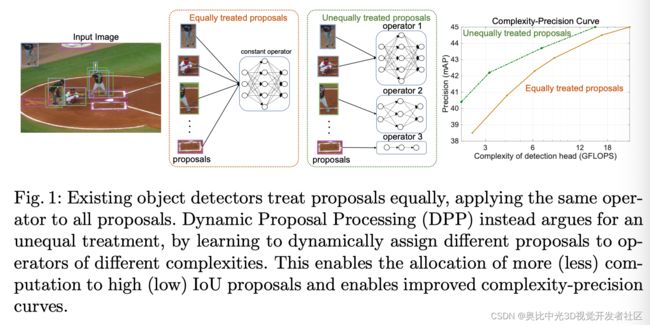
在这项工作中,作者研究是否有可能在降低其计算成本的同时保留现代检测头的精度增益和proposal稀疏性,从而使其适用于高效的对象检测设计。作者注意到,现有高端检测器的主要限制是它们平等地对待所有proposal,从某种意义上说,检测头适用于具有相同复杂性的操作的所有proposal,并保持每个proposal的恒定成本。
然而,这是不直观的。虽然在好的proposal上花费大量计算似乎是适当的,但将同等资源分配给差的proposal是浪费。由于每个proposal的IoU在训练期间是已知的,因此检测器原则上可以学习将不同的计算量分配给不同的proposal。然而,这需要检测器设计的范式转换,如上图所示:不同的proposal应在资源分配方面得到不平等的对待,为高质量proposal保留比低质量proposal更多的计算。
困难在于,由于IOU在推理时不可用,网络必须学会动态执行资源分配。这意味着需要一个资源分配函数,该函数取决于proposal本身,必须学习,即动态网络模块。
为了解决这个问题,作者提出了动态proposal处理(DPP)框架,其中现有检测头的单个操作被一个算子集取代,该算子集由多个不同复杂度的算子组成。这种方法的好处是允许检测器在复杂度-精度曲线的多个点上逐个proposal操作,从而优化两个目标之间的总体权衡。这是通过添加选择模型来实现的,该模型在网络的每个阶段选择适用于每个proposal的最佳操作。
作者证明,该选择器可以是非常轻量级的,是一个多层感知器,在操作索引上输出一个one-hot代码,并在训练时以端到端的方式学习。这是通过引入两个新的损失函数实现的,这两个函数共同鼓励将可用的计算预算分配给大型IoU的proposal。IoU损失教会检测器识别大型IoU的proposal,并改进其与ground truth边界框的对齐。复杂性损失使选择器知道每个图像的实例数,以便动态控制计算资源的分配并满足总体计算目标。
COCO数据集上的实验结果表明,与同等对待proposal的设计相比,DPP实现了更好的复杂度-精度曲线,尤其是在低复杂度区域,证实了不平等对待proposal的有效性。
对于大型主干网,DPP实现了文献中精度最佳的复杂度曲线,以当前模型60%的计算量实现了最先进的精度。对于低复杂度网络,增益更为显著,因为DPP在精度和计算方面建立了最先进的技术,并产生了最佳延迟精度曲线。
3. Complexity and Precision of Proposals
在本节中,作者比较了平等或不平等对待proposal的复杂性。假设主干产生一组 X = { x 1 , x 2 , … , x N } \boldsymbol{X}=\left\{\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \ldots, \boldsymbol{x}_{N}\right\} X={x1,x2,…,xN}proposal,并关注检测头的成本,即忽略主干成本。
作者进一步假设检测头的计算可以分解为每个proposal算子h(例如网络块)和成对分量p,这个分量包括proposal间计算的成本。例如,经典检测器的NMS操作或Transformer proposal之间的自注意力机制。
Complexity of equally treated proposals
在以前的工作中,所有proposal都由同一个运算符h处理。复杂性如下:
C ( ψ ) = ∑ i = 1 N C h s i + N ( N − 1 ) 2 C p \mathcal{C}(\psi)=\sum_{i=1}^{N} C_{h_{s_{i}}}+\frac{N(N-1)}{2} C_{p} C(ψ)=i=1∑NChsi+2N(N−1)Cp
其中 s i = s ( x i ) , h s i ∈ G s_{i}=s\left(\boldsymbol{x}_{i}\right), h_{s_{i}} \in \mathcal{G} si=s(xi),hsi∈G表示G中的算子,该算子由选择器s分配给proposal ψ = { { h s i } i , s , p } , C h s i \psi=\left\{\left\{h_{s_{i}}\right\}_{i}, s, p\right\}, C_{h_{s_{i}}} ψ={{hsi}i,s,p},Chsi 是每个proposal操作(选择器加算子)的复杂度。为了简单起见,成对复杂性仍然被认为是恒定的。
Precision over proposals
当检测头不平等地对待proposals时,可以通过优化算子对proposals的分配来确定给定复杂度约束C的最佳检测器精度:
P ( ψ ∗ ∣ C ) = max h s i ∈ G c ( ψ ) < C P ( { h s i } i ) P\left(\psi^{*} \mid C\right)=\max _{\substack{h_{s_{i}} \in \mathcal{G} \\ \mathcal{c}(\psi)
其中 P ( { h s i } i ) \mathcal{P}\left(\left\{h_{s_{i}}\right\}_{i}\right) P({hsi}i) 是特定算子赋值 { h s i } i \left\{h_{s_{i}}\right\}_{i} {hsi}i 的精度。随着C的变化, P ( ψ ∗ ∣ C ) P\left(\psi^{*} \mid C\right) P(ψ∗∣C) 形成复杂度-精度(C-P)曲线,在成本和精度之间的权衡方面,表征可使用 G \mathcal{G} G 实现的对象检测器的最佳性能。
在这项工作中,作者使用精度(mAP)和C-P曲线作为标准来证明不平等处理proposal的有效性。请注意,在给定计算预算C下,将运算符分配给proposal是优化精度的关键。这是一个可以通过简单网络分支实现的学习函数,并通过适当的损失函数求解。
4. Dynamic Proposal Processing
在本节中,作者提出了一个动态proposal处理(DPP)框架。根据先前工作的设计,假设探测头由多个阶段 ( ψ = ϕ 1 ∘ … ∘ ϕ K ) \left(\psi=\phi_{1} \circ \ldots \circ \phi_{K}\right) (ψ=ϕ1∘…∘ϕK) 组成,按顺序处理proposal。每个阶段 ϕ K \phi_{K} ϕK 由选择器s从 G \mathcal{G} G 中选择一个运算符来实现。为了最小化复杂性,选择器只能应用于子集 k ∈ K ⊂ { 1 , … , K } k \in \mathcal{K} \subset\{1, \ldots, K\} k∈K⊂{1,…,K}, 其余阶段使用为其前一个阶段选择的运算符,即 ϕ k = ϕ k − 1 , ∀ k ∉ K \phi_{k}=\phi_{k-1}, \forall k \notin \mathcal{K} ϕk=ϕk−1,∀k∈/K。
4.1 Operator Set
在本文中,作者考虑一个算子集 G = { g 0 , g 1 , g 2 } \mathcal{G}=\left\{g_{0}, g_{1}, g_{2}\right\} G={g0,g1,g2},由三个计算量非常不同的算子组成。具体来说, g 0 g_{0} g0是一种高复杂度算子,由proposal相关参数的动态卷积层(DyConv)和前馈网络(FFN)实现。该算子基于最近Sparse R-CNN中采用的动态头结构。 g 1 g_{1} g1是一个中等复杂度的算子,用静态FFN实现。最后, g 1 g_{1} g1是由一个identity块形成的轻量级算子,该identity块仅向前传送proposal,而无需进一步细化。
4.2 Selector
在DPP中,选择器是控制精度和复杂度之间权衡的关键组件,通过控制运算符对proposal的分配。设 z i k z_{i}^{k} zik 是proposal x i x_{i} xi在阶段 ϕ K \phi_{K} ϕK 输入处的嵌入。选择器由一个3层MLP实现,该MLP将 z i k z_{i}^{k} zik 关联一个三维向量 ϵ i k ∈ [ 0 , 1 ] 3 \epsilon_{i}^{k} \in[0,1]^{3} ϵik∈[0,1]3:
ϵ i k = MLP ( z i k ) \epsilon_{i}^{k}=\operatorname{MLP}\left(\boldsymbol{z}_{i}^{k}\right) ϵik=MLP(zik)
其中 ϵ i , j k \epsilon_{i, j}^{k} ϵi,jk 是 ϵ i k \epsilon_{i}^{k} ϵik 中的选择变量,表示算子 g j g_{j} gj 对proposal x i x_{i} xi 的赋值强度。在训练期间,选择向量是三个变量上的one-hot码,并且使用Gumble Softmax函数作为MLP的激活来生成选择向量。
对于推理,选择变量具有soft值,并选择与具有最大值的选择变量的索引匹配的运算符。操作分配过程的流程图如下图所示。请注意,提出的选择器非常轻(在本文的实验设置中,100个proposal使用4e-3 GFLOP),事实上,与检测头相比,这些复杂性可以忽略不计。
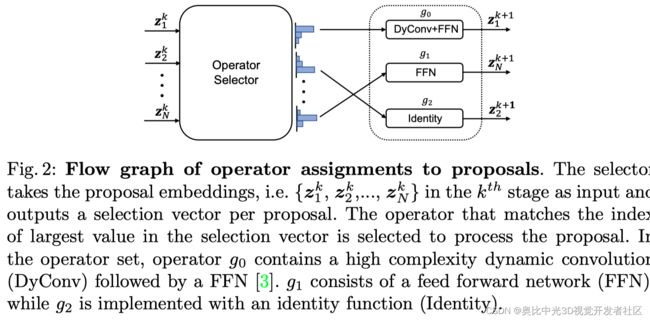
所选的算子在proposal i i i 和head阶段 k k k 之间都不同,从而能够以动态方式不平等地处理proposal i i i 。
此外,虽然 G \mathcal{G} G 基数是3,但可用于实现检测器头的一组网络架构的基数为 3 ∣ K ∣ 3^{|\mathcal{K}|} 3∣K∣。最后,由于选择器是可训练的,因此可以端到端学习分配函数。
4.3 Loss Functions
为了确保在给定复杂度预算的情况下,DPP为每个proposal选择最优的算子序列,选择损失应用于K中每个阶段的选择器。该选择损失旨在鼓励实现两个目标。首先,应将复杂操作分配给高质量proposal(大型IoU),因为这些proposal需要检测头进行大部分额外工作。这是通过IoU损失强制执行的:
L i o u = 1 N ∑ i = 1 N ∑ k ∈ K ∑ j ∈ { 0 , 1 } ( 1 − u i k ) ϵ i , j k + u i k ( 1 − ϵ i , j k ) L_{i o u}=\frac{1}{N} \sum_{i=1}^{N} \sum_{k \in \mathcal{K}} \sum_{j \in\{0,1\}}\left(1-u_{i}^{k}\right) \epsilon_{i, j}^{k}+u_{i}^{k}\left(1-\epsilon_{i, j}^{k}\right) Liou=N1i=1∑Nk∈K∑j∈{0,1}∑(1−uik)ϵi,jk+uik(1−ϵi,jk)
其中 u i k u_{i}^{k} uik 是第k阶段第i个proposal的IoU。 L i o u L_{i o u} Liou 使用选择器将 ϵ i , 1 k \epsilon_{i, 1}^{k} ϵi,1k 和 ϵ i , 0 k \epsilon_{i, 0}^{k} ϵi,0k 转换为“0”,对于IoU小于0.5的proposal,则转换为“1”。这鼓励在阶段k中使用更复杂的运算符来处理高质量proposal。
此外,损失幅度由IoU值确定,当选择器将小IoU proposal预测为“1”或大型proposal预测为“0”时,会产生较大的梯度。其次,选择器应该知道每个图像中实例的总数,并根据其调整总体复杂度,即当实例密集时选择更复杂的算子。这是通过复杂性损失来实现的:
L c = 1 N ∑ k ∈ K ∣ ∑ i = 1 N ϵ i , 0 k − T ∣ L_{c}=\frac{1}{N} \sum_{k \in \mathcal{K}}\left|\sum_{i=1}^{N} \epsilon_{i, 0}^{k}-T\right| Lc=N1k∈K∑∣ ∣i=1∑Nϵi,0k−T∣ ∣
其中T是为特定图像选择算子 g 0 g_{0} g0 的目标次数。这被定义为 T = α M T=\alpha M T=αM, 其中 α \alpha α 是指定图像中M个对象实例的倍数的乘数。此外,条件 T ∈ [ T min , N ] T \in\left[T_{\min }, N\right] T∈[Tmin,N] 通过根据预先指定的下界 T min T_{\min } Tmin和由总proposal数N给出的上界剪裁 α M \alpha M αM来强制执行。下限防止了高复杂度算子 g 0 g_{0} g0 和 α \alpha α 的稀疏选择,然后根据实例数调整选择器。 α , T min , N \alpha,T_{\min },N α,Tmin,N是超参数,可用于修改DPP的行为。
最终确定总体选择损失为:
L s = L i o u + λ L c L_{s}=L_{i o u}+\lambda L_{c} Ls=Liou+λLc
其中λ是控制损耗分量之间权衡的超参数。请注意,选择损失是一种即插即用损失,可应用于不同的物体检测器。在本文中, L s L_{s} Ls与应用DPP的原始检测器的所有损失相结合,包括交叉熵损失和边界框回归损失。
5. 实验
上表显示了不同操作处理的proposal的精度。表示COCO验证集中评估的平均proposal数。 N e v a l N_{eval} Neval 表示COCO验证集中评估的平均proposal数。
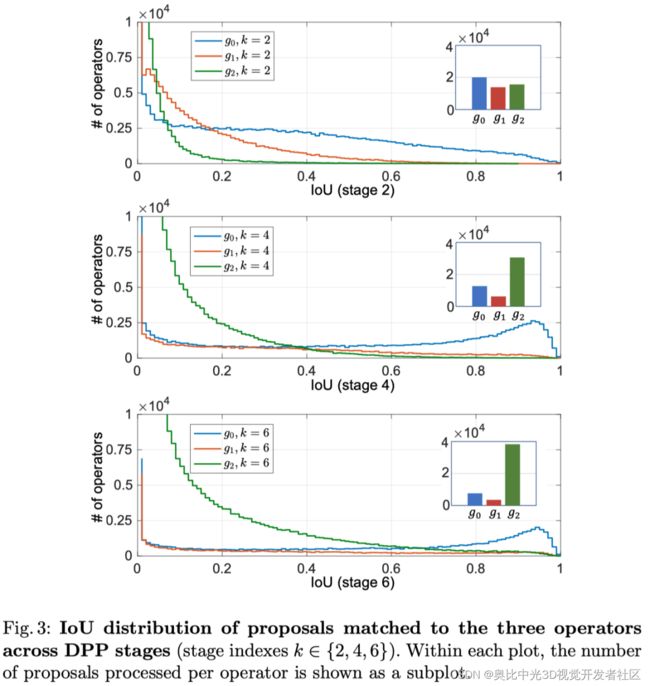
不同操作选择的方案的IoU分布如上图所示。每个操作处理的proposal总数以子图表示。
上图以高复杂度算子 g 0 g_{0} g0在第4和第6阶段预测的边界框的形式显示了一些定性结果。在第6阶段(右栏)中预测的框与ground truth(左栏)有很好的重叠,但重复有限。
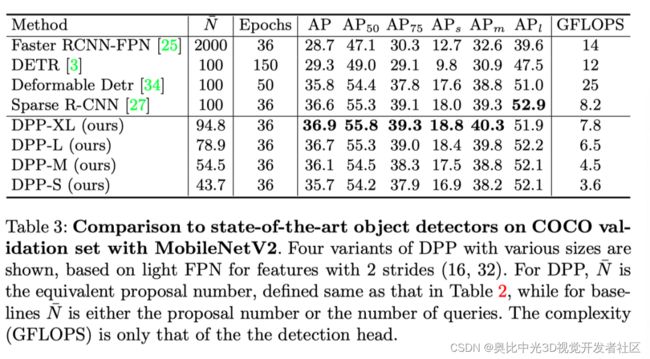
上表展示了在ResNet和MobileNet下和本文方法和SOTA结果的对比。
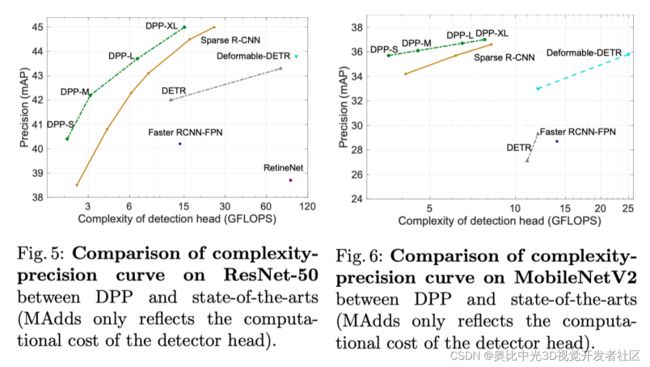
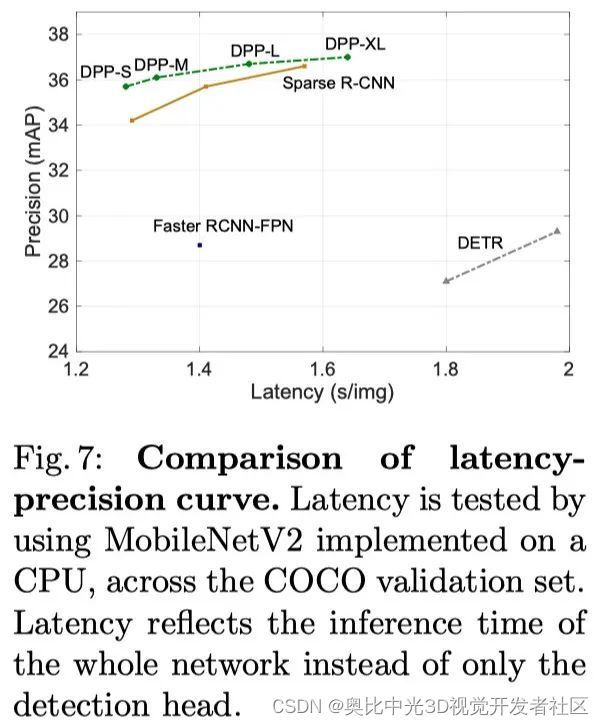
上图展示了在ResNet和MobileNet下和本文方法和SOTA复杂度的对比。
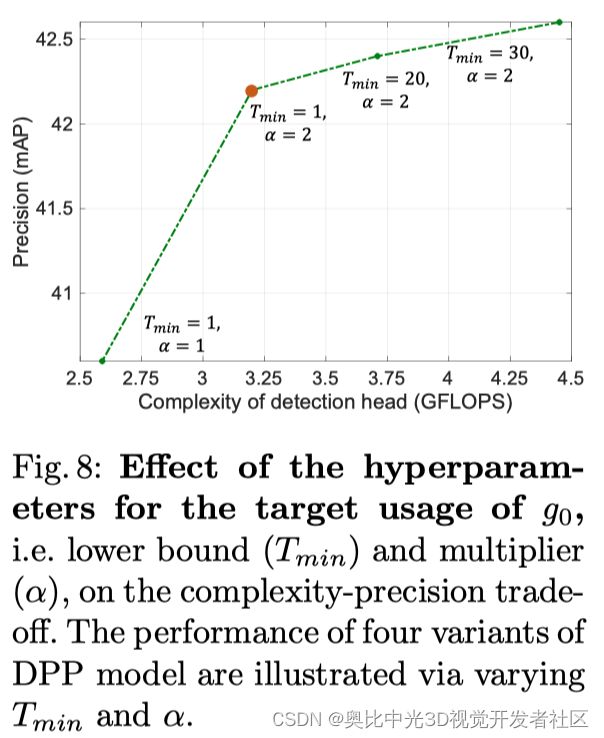
上图展示了超参数对 g 0 g_{0} g0目标使用的影响。
上表展示了超参数λ对DPP选择损失的影响。
6. 总结
在本文中,作者提出不平等地对待目标检测的proposal。通过动态proposal处理(DPP)框架设计和优化提议和运算符之间的匹配问题,该框架包含一个简单选择器,由两个损失函数(IoU损失和复杂性损失)监督。实验结果表明,在较宽的复杂度范围内,DPP框架在不同类型的主干上实现了最先进的复杂度-精度权衡。
参考资料
[1]https://arxiv.org/abs/2207.03520
[2]https://github.com/liyunsheng13/dpp
版权声明:本文为奥比中光3D视觉开发者社区特约作者授权原创发布,未经授权不得转载,本文仅做学术分享,版权归原作者所有,若涉及侵权内容请联系删文。
3D视觉开发者社区是由奥比中光给所有开发者打造的分享与交流平台,旨在将3D视觉技术开放给开发者。平台为开发者提供3D视觉领域免费课程、奥比中光独家资源与专业技术支持。点击加入[3D视觉开发者社区],和开发者们一起讨论分享吧~