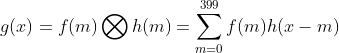高斯低通频率域滤波

基本原理

        频率域滤波，即将原图像通过傅里叶变换，转换至频率域，在频率域利用该域特有的性质进行处理，再通过傅里叶反变换把处理后的图像返回至空间域。所以，频率域的操作是在图像的傅里叶变换上执行，而不是在图像本身上执行。 

        高斯低通滤波器传递函数表达式为：

        其中  是点 ( u , v ) 到中心点的距离， 是截止频率 

        由表达式可知，高斯函数的傅里叶变换仍为高斯函数，在图形方面，高斯函数平滑过渡低频与高频，无明显截止的尖锐不连续，且值为非负，所以高斯滤波无振铃现象

---

         图像填充0的重要性

        在进行离散傅里叶变换时，自动将该空间函数进行周期化（频率域的离散化对应着空间域的周期化），所以当使用傅里叶变换得出卷积函数时，错误地处理周期性将得到错误的结论。

        假设某函数为  ，长度为400；传递函数为  ，长度为400

        卷积结果为：

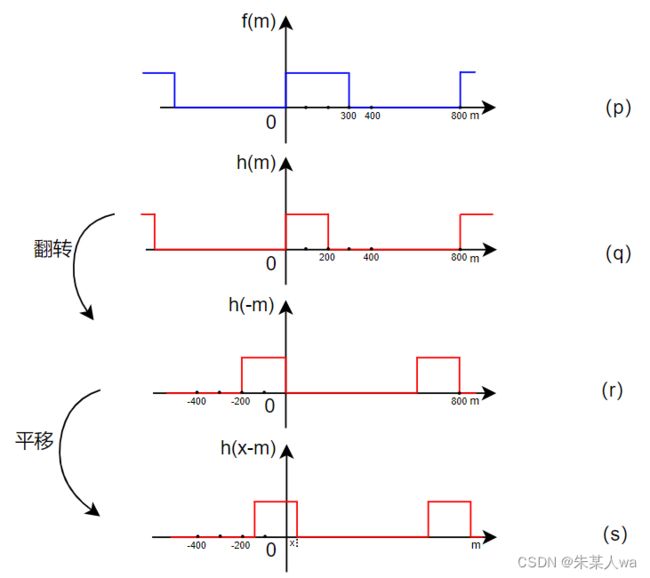
        由上述表达式可知，在计算卷积时，先对其中一个函数例如  关于y轴翻折，得 

再将其按照 x 进行平移，记作 ，每次平移，计算 m = 0,1,2,3,,,,399 对应点的相乘相加值，即为该 x 点的卷积值。

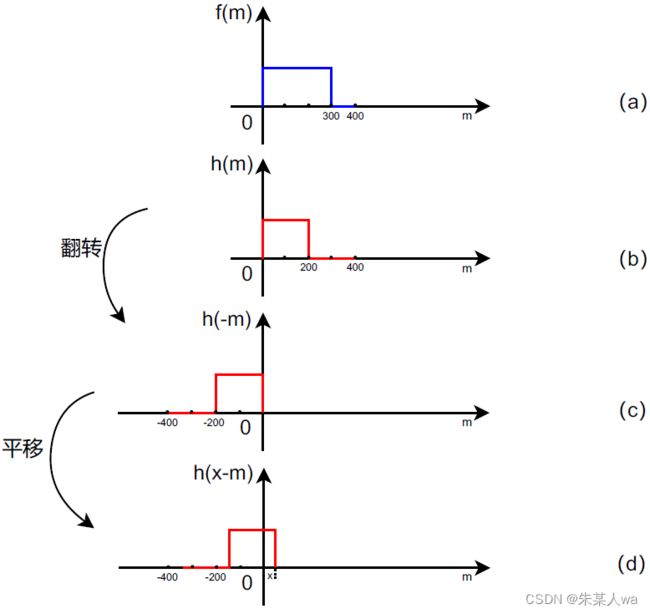
• 预期达到的结果：

     

        图(h)表示卷积期望所得结果，可以看出，卷积是位移变量 x 的函数，其范围从 0 到 400+400-1 = 799

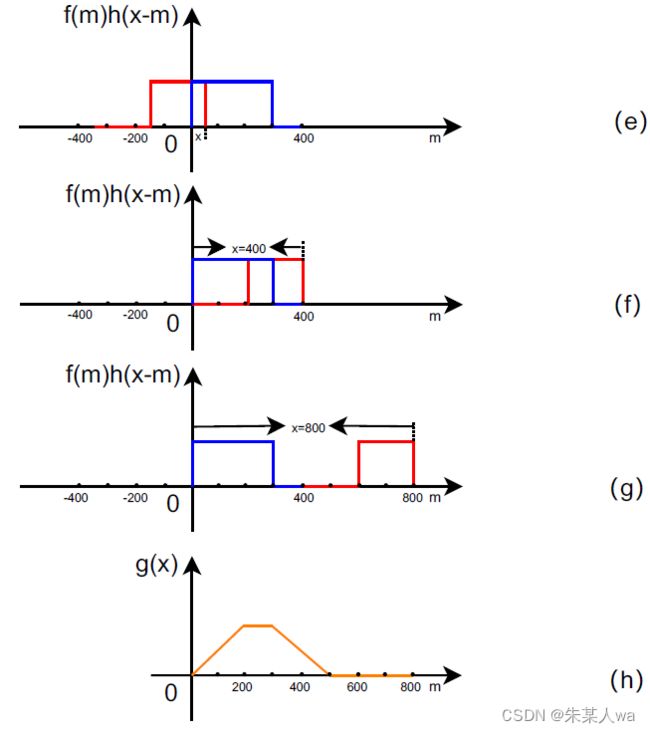
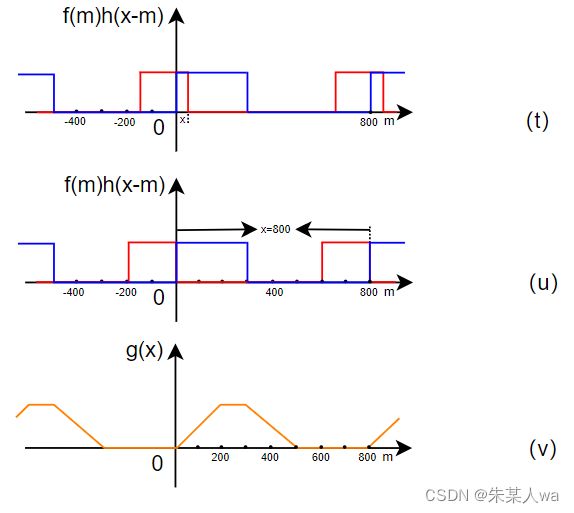
•  若按照原图像大小进行离散傅里叶变换，所达到的结果：

         离散傅里叶变换，相当于在空间域中，对原函数进行周期延拓，如原函数长为400，则执行傅里叶变换（相当于，以400为周期对函数进行周期延拓）。最终结果如图 (o) 绿色曲线所示，显然不为图 (h) 所期望图形，该现象称为频率混叠。主要原因是在移位相乘相加过程中，其它周期的值对当前周期的值产生影响，造成结果错误。解决方法为对原函数进行填充0操作，如此，在进行傅里叶变换时，对填充后的图像进行周期延拓，其它周期的值对当前周期的值不会产生影响

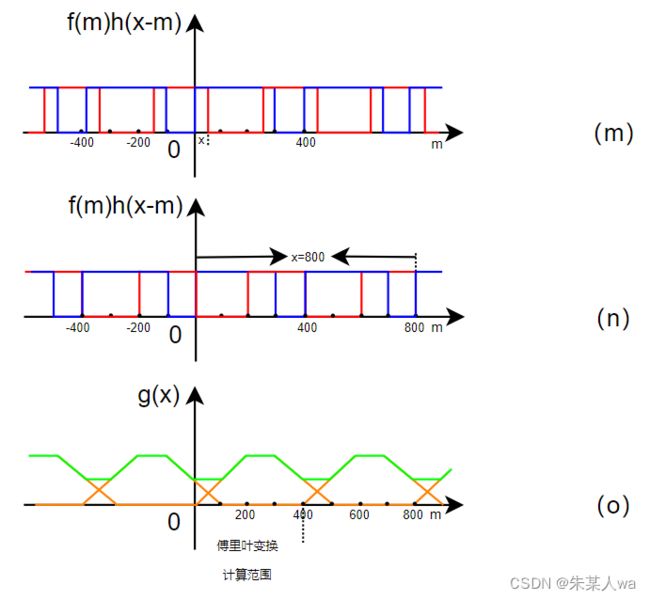
• 若将该图像进行拓展后，再进行离散傅里叶变换，所达到的结果：

         将图片填充0后，再进行傅里叶变换，周期延拓不影响卷积结果，如图 (v) 所示，在 0 到   799 范围内所得结果与预期结果保持一致

        结论：

        图像进行周期延拓，目的是防止出现频率混叠，影响滤波效果，保证循环卷积是我们原本滤波所需的线性卷积。

Matlab编程实现

频率域高斯低通滤波实现大致步骤：

1. 给定图像   ，大小为 row×col，在空间域对图像进行填充，填充后图像大小为 P = 2×row，Q = 2×col，之后进行中心化，傅里叶变换，至频率域，得 
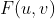
2. 生成一个传递函数 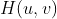 ，大小为 P×Q ，中心位于（ P/2，Q/2 ），与  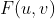中心化相对应
3. 用阵列相乘得 
4. 将得到的结果进行傅里叶反变换，去中心化，取实部（忽略由于计算不准确导致的寄生复成分），最后取出左上角原图像 row×col 大小的区域，得到频率域滤波结果

代码实现

clear;
clc;
close all;

%读入图像
i = imread('saturn.png');
I = rgb2gray(i);
figure;
subplot(131);
imshow(I);
title('原始图像');
I = imnoise(I,'salt & pepper');%加入椒盐噪声
subplot(132);
imshow(I);
title('加入椒盐噪声图像');
%对图像进行延拓
[row,col] = size(I);
P = row*2;
Q = col*2;
image = zeros(P,Q);
image(1:row,1:col) = double(I);
%采用傅立叶变换并频谱中心化
F = fft2(image); 
F = fftshift(F); 
%找出中心点的坐标
center_x = fix(P/2);
center_y = fix(Q/2);
%高斯低通滤波
D0 = 100;%滤波器截止频率
H = zeros(P,Q);
for i=1:P
    for j=1:Q
        d = (i-center_x)^2+(j-center_y)^2;
        H(i,j) = exp((-d/(2*D0*D0)));
        H(i,j) = H(i,j)*F(i,j);
    end
end
%频谱去中心化并傅立叶反变换
out = ifft2(ifftshift(H));
out = uint8(real(out));
%输出图像
output = out(1:row,1:col);
subplot(133);
imshow(output);
title('高斯低通滤波后图像');

运行结果

        通过改变截止频率  的大小来达到改变高斯低通滤波器的滤波效果

        实际上，在空间域滤波与在频率域滤波的效果相同，联系两个域的纽带为卷积定理

写在最后

        以上仅个人实验想法，若存在错误或者更优解法，欢迎大家指出。