Python中范数计算以及numpy矩阵的运算

Python中范数计算以及numpy矩阵的运算

一、范数

1.1 定义：

​ 范数(norm)是数学中的一种基本概念。在泛函分析中，它定义在赋范线性空间中，并满足一定的条件，即①非负性；②齐次性；③三角不等式。它常常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小。
​ 最常见的范数就是p范数。若$x=[x_1,x_2...x_n{]}^T$，那么
$${\Vert x\Vert }_p=(|x_1{|}^p+|x_2{|}^p+...+|x_n{|}^p{)}^{\frac{1}{p}}$$
​ 当$p=1,2,\infty $时分别是以下集中情况：

$$\begin{gathered} {\Vert x\Vert }_1=|x_1|+|x_2|+...+|x_n| \\ {\Vert x\Vert }_2=(|x_1{|}^2+|x_2{|}^2+...+|x_n{|}^2{)}^{\frac{1}{2}} \\ {\Vert x\Vert }_p=max(|x_1|,|x_2|,...,|x_n|) \end{gathered}$$
常用的三种范数的范数矩阵：

​ 1范数：列和范数，每一列元素之和的最大值。

​ 2范数：谱范数，矩阵中所有元素平方和开根号。

​ $\infty$范数：行和范数，每一行之和的最大值。

二、numpy中范数计算

1）基本语法：

np.linalg.norm(x,ord=None,axis=None)	# x代表矩阵，ord代表范数类型

参数	范数类型
ord=2或None	二范数
ord=1	一范数
ord=np.Inf	无穷范数

2）axis为处理方向：

• axis=1时表示按行向量处理，求多个行向量的范数
• axis=0时表示按列向量处理，求多个列向量的范数。

2.1 实际案例

案例一：对矩阵求范数

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
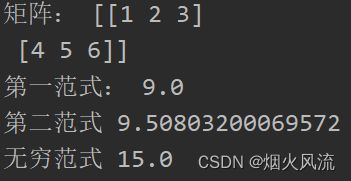
print("矩阵：",a)

a1=np.linalg.norm(a,ord=1)
print("第一范式：",a1)
a2=np.linalg.norm(a,ord=2)
print("第二范式",a2)
a3=np.linalg.norm(a,ord=np.Inf)
print("无穷范式",a3)

案例二：对矩阵的行向量求范数

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
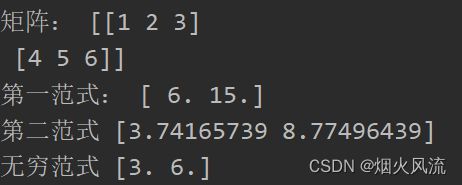
print("矩阵：",a)

a1=np.linalg.norm(a,ord=1,axis=1)
print("第一范式：",a1)
a2=np.linalg.norm(a,ord=2,axis=1)
print("第二范式",a2)
a3=np.linalg.norm(a,ord=np.Inf,axis=1)
print("无穷范式",a3)

案例三：对矩阵的列向量求范数

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
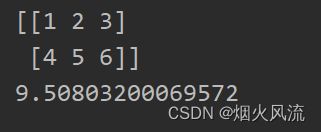
print("矩阵：",a)

a1=np.linalg.norm(a,ord=1,axis=0)
print("第一范式：",a1)
a2=np.linalg.norm(a,ord=2,axis=0)
print("第二范式",a2)
a3=np.linalg.norm(a,ord=np.Inf,axis=0)
print("无穷范式",a3)

三、numpy矩阵运算

​ numpy矩阵之间的四则运算，根据两矩阵之间的各个元素一一对应进行。例如：
$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]+\left[\begin{array}{ccc}1& 2& 3\end{array}\right]=\left[\begin{array}{ccc}2& 4& 6\\ 5& 7& 9\end{array}\right]$$
​ 如果说要进行线性代数中矩阵相乘需要调用包中的.dot方法进行运算。

3.1 numpy矩阵加减

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
b=np.array([2,2,2])
print("两矩阵相加：\n",a+b)
print("两矩阵相减：\n",a-b)

3.2 numpy矩阵乘除

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
b=np.array([2,2,2])
print("两矩阵相除：\n",a/b)
print("两矩阵相乘：\n",a*b)

3.3 矩阵乘法运算

import numpy as np
a=np.array([[1,2,3],[4,5,6]])
c=np.array([[2],[2],[2]])
print("矩阵乘法运算\n",np.dot(a,c))