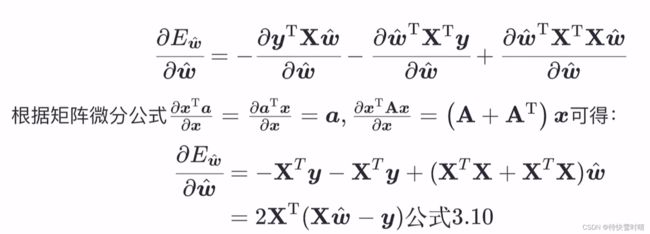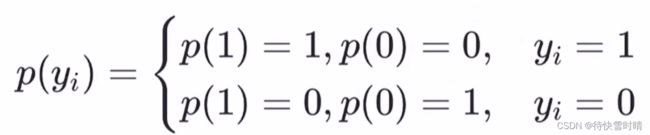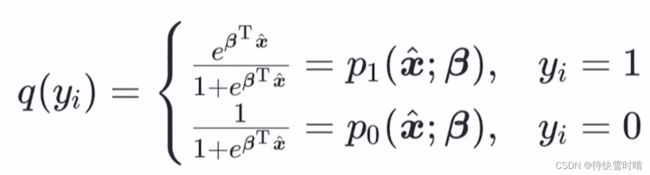【机器学习】西瓜书 03 线性回归模型
03 线性模型
文章目录
- 03 线性模型
-
- 机器学习三要素
- 3.1 一元线性回归算法原理
-
- 3.1.1最小二乘法
- 3.1.2极大似然估计法
- 3.2 参数估计
-
- 凸集
- 凸函数
- 凸充分性定理
- 梯度
- Hessian矩阵
- 3.2.1证明 E ( w , b ) E_{(w,b)} E(w,b)是关于 w w w和 b b b的凸函数
- 3.2.2求解损失函数的参数
- 3.2.3向量化
- 3.2.4 多元线性回归
- 3.2.5 矩阵微分
- 3.2.6 对数线性回归
- 3.3 Logistic 回归 (解决分类问题)
-
- 3.3.1 联系函数
- 3.3.2 参数估计
-
- 3.3.2.1 极大似然估计
- 3.3.2.2 信息熵
-
- 自信息
- 信息熵
- 相对熵(KL散度)
- 3.4 线性判别分析
-
- 广义特征值
- 广义瑞利商
机器学习三要素
- 模型:根据具体问题,确定假设空间
- 策略:根据评价标准,确定选取最优模型的策略(通常会导出一个损失函数)
- 策略一:最小二乘法
- 策略二:极大似然估计法
- 算法:求解损失函数,确定最优模型
- 闭式解
- 近似最值解
3.1 一元线性回归算法原理
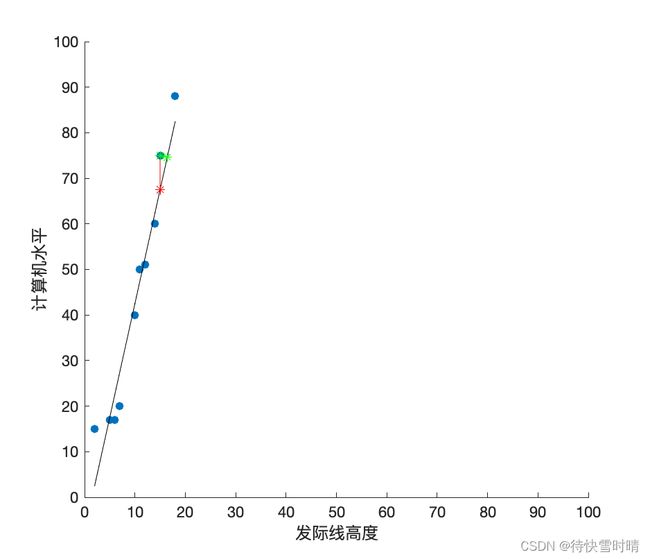
考虑这样一个问题:我们拥有程序员的发际线高度 X = x 1 , x 2 , . . . x i , . . . x m X={x_1,x_2,...x_i,...x_m} X=x1,x2,...xi,...xm,和她们的计算机水平 Y = y 1 , y 2 , . . . , y i , . . . , y m Y={y_1,y_2,...,y_i,...,y_m} Y=y1,y2,...,yi,...,ym的一批数据,现在来研究这两者之间的关系。根据数据散点图,我们可以直观地画出一条直线 f ( x ) = w x + b f(x)=wx+b f(x)=wx+b,令这些数据点 ( x i , y i ) (x_i,y_i) (xi,yi)到直线的距离最短,那么这条直线就是所求的线性回归模型。其中,观察点到直线的距离,可以是垂直距离(绿色线段),也可以是欧式距离 y − f ( x ) y-f(x) y−f(x)(红色线段)。我们把依赖于前者的方法叫作正交回归,依赖于后者的方法叫作线性回归。
上述问题是简单的一元回归问题,从发际线高度这一特征,来预测其计算机水平。当然还有很多其他的案例,比如信用卡额度预测问题,特征是用户的信息(如年龄,性别,年薪……),我们来预测给用户多大的信用额度,这样类似的问题都是回归问题,目标值 y y y 隶属于实数空间 R R R 。
根据输入特征的数目和特征值之间的“序”关系,我们可以对特征取值进行转化。
-
仅通过 发际线高度 预测 计算机水平:
f ( x ) = w 1 x 1 + b f(x)=w_1x_1+b f(x)=w1x1+b
-
+二值离散特征 颜值 (好看:1,不好看:0)
f ( x ) = w 1 x 1 + w 2 x 2 + b f(x)=w_1x_1+w_2x_2+b f(x)=w1x1+w2x2+b
-
+有序的多值离散特征 饭量 (小:1,中:2,大:3)
f ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + b f(x)=w_1x_1+w_2x_2+w_3x_3+b f(x)=w1x1+w2x2+w3x3+b
-
+无序的多值离散特征 肤色 (黄:[1,0,0],黑:[0,1,0],白:[0,0,1])
f ( x ) = w 1 x 1 + w 2 x 2 + w 3 x 3 + w 4 x 4 + w 5 x 5 + w 6 x 6 + b f(x)=w_1x_1+w_2x_2+w_3x_3+w_4x_4+w_5x_5+w_6x_6+b f(x)=w1x1+w2x2+w3x3+w4x4+w5x5+w6x6+b
3.1.1最小二乘法
本书中讨论的是线性回归问题,线性回归假设 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b。我们用均方误差作为回归问题中的性能度量,得到损失函数 E ( w , b ) E_{(w,b)} E(w,b)。
E ( w , b ) = Σ i = 1 m ( y i − f ( x i ) ) 2 = Σ i = 1 m ( y i − w x i − b ) 2 E_{(w,b)}=\Sigma_{i=1}^m(y_i-f(x_i))^2=\Sigma_{i=1}^m(y_i-wx_i-b)^2 E(w,b)=Σi=1m(yi−f(xi))2=Σi=1m(yi−wxi−b)2
基于均方误差最小化对模型求解的方法称为 最小二乘法(Least Square Method),表达式为 arg min ( w , b ) Σ i = 1 m ( y i − w x i − b ) 2 \arg\min_{(w,b)}\Sigma_{i=1}^m(y_i-wx_i-b)^2 argmin(w,b)Σi=1m(yi−wxi−b)2,这里的 arg min ( w , b ) \arg\min_{(w,b)} argmin(w,b)表示求解使得式子达到最小值的 w w w和 b b b。
3.1.2极大似然估计法
根据一元线性回归公式推导,我们发现使用极大似然估计(Maximum Likelihood Estimation)可以得到同样的损失函数。
目的:估计概率分布的参数值,如正态分布的参数均值和方差 μ , σ 2 \mu,\sigma^2 μ,σ2
方法:对于离散随机变量 X = { x 1 , x 2 , . . . , x n } X=\{x_1,x_2,...,x_n\} X={x1,x2,...,xn}, x i x_i xi是已知的独立同分布(i.i.d)随机变量,假设概率质量函数 P ( x ; θ ) P(x;\theta) P(x;θ), θ \theta θ为待估计的参数(可以是多个参数),那么 似然函数 为 L ( θ ) = ∏ i = 1 n P ( x i ; θ ) L(\theta)=\prod_{i=1}^nP(x_i;\theta) L(θ)=∏i=1nP(xi;θ)。我们考虑使得观测样本出现概率最大的分布,就是所求的分布。
根据线性回归假设,再考虑随机误差 ϵ ∼ N ( 0 , σ 2 ) \epsilon \sim N(0,\sigma^2) ϵ∼N(0,σ2),我们可以得到线性模型 y = w x + b + ϵ y=wx+b+\epsilon y=wx+b+ϵ。
根据正态分布概率密度函数公式, p ( ϵ ) = 1 2 π σ exp ( − ϵ 2 2 σ 2 ) p(\epsilon)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{\epsilon^2}{2\sigma^2}) p(ϵ)=2πσ1exp(−2σ2ϵ2),
把 ϵ = y − w x − b \epsilon=y-wx-b ϵ=y−wx−b代入上述公式,得到 y y y的概率密度函数: p ( y ) = 1 2 π σ exp ( − ( y − ( w x + b ) ) 2 2 σ 2 ) p(y)=\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y-(wx+b))^2}{2\sigma^2}) p(y)=2πσ1exp(−2σ2(y−(wx+b))2),
即 y ∼ N ( w x + b , σ 2 ) y \sim N(wx+b,\sigma^2) y∼N(wx+b,σ2)。
计算似然函数 L ( w , b ) = ∏ i = 1 m p ( y i ) = ∏ i = 1 m 1 2 π σ exp ( − ( y i − ( w x i + b ) ) 2 2 σ 2 ) L(w,b)=\prod_{i=1}^mp(y_i)=\prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{(y_i-(wx_i+b))^2}{2\sigma^2}) L(w,b)=∏i=1mp(yi)=∏i=1m2πσ1exp(−2σ2(yi−(wxi+b))2),
为了便于计算,对似然函数取对数,变乘为加, ln L ( w , b ) = Σ i = 1 m ln 1 2 π σ + Σ i = 1 m ln exp ( − ( y i − ( w x i + b ) ) 2 2 σ 2 ) = m ln 1 2 π σ + − 1 2 σ 2 Σ i = 1 m ( y i − ( w x i + b ) ) 2 \ln L(w,b)=\Sigma_{i=1}^m\ln\frac{1}{\sqrt{2\pi}\sigma}+\Sigma_{i=1}^m\ln\exp(-\frac{(y_i-(wx_i+b))^2}{2\sigma^2})=m\ln\frac{1}{\sqrt{2\pi}\sigma}+-\frac{1}{2\sigma^2}\Sigma_{i=1}^m(y_i-(wx_i+b))^2 lnL(w,b)=Σi=1mln2πσ1+Σi=1mlnexp(−2σ2(yi−(wxi+b))2)=mln2πσ1+−2σ21Σi=1m(yi−(wxi+b))2
对 ln L ( w , b ) \ln L(w,b) lnL(w,b)取最大值,可等价于对 Σ i = 1 m ( y i − ( w x i + b ) ) 2 \Sigma_{i=1}^m(y_i-(wx_i+b))^2 Σi=1m(yi−(wxi+b))2取最小值,即 arg min ( w , b ) Σ i = 1 m ( y i − w x i − b ) 2 \arg\min_{(w,b)}\Sigma_{i=1}^m(y_i-wx_i-b)^2 argmin(w,b)Σi=1m(yi−wxi−b)2,与最小二乘法殊途同归。
3.2 参数估计
由最小二乘法和极大似然函数估计法,我们得到同一个 E ( w , b ) E_{(w,b)} E(w,b),接下来对参数 w w w和 b b b进行求解,即参数估计。
首先 E ( w , b ) E_{(w,b)} E(w,b)是关于 w w w和 b b b的凸函数 ,那么当它关于二者的 导数 均为零时,就得到了 w w w和 b b b的最优解。
为了理解并求证“ E ( w , b ) E_{(w,b)} E(w,b)是关于 w w w和 b b b的凸函数”这一含义,这里需明确一些概念。
凸集
数学定义: x , y ∈ D x,y\in D x,y∈D,任意 α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1],存在 α x + ( 1 − α ) y ∈ D \alpha x+(1-\alpha)y \in D αx+(1−α)y∈D,那么 D D D是凸集。
几何意义:两点属于一个集合,且两点连线上任意一点都属于此集合,称为凸集。
凸函数
数学定义:对区间 [ a , b ] [a,b] [a,b]上定义的函数 f f f,若它对区间中任意两点 x 1 , x 2 x_1,x_2 x1,x2均有 f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f(\frac{x_1+x_2}{2})\leq \frac{f(x_1)+f(x_2)}{2} f(2x1+x2)≤2f(x1)+f(x2),则称 f f f为区间 [ a , b ] [a,b] [a,b]上的凸函数。
例子:U型函数如 f ( x ) = x 2 f(x)=x^2 f(x)=x2
凸充分性定理
若 f f f是凸函数,且 f ( x ) f(x) f(x)一阶连续可微,则 x ∗ x^* x∗是全局解的充要条件是 ∇ f ( x ∗ ) = 0 \nabla f(x^*)=0 ∇f(x∗)=0。
梯度
多元函数的一阶导数,对各个分量求偏导。
Hessian矩阵
同上,取二阶偏导数。
3.2.1证明 E ( w , b ) E_{(w,b)} E(w,b)是关于 w w w和 b b b的凸函数
根据定理:设 D D D是非空开凸集, f ( x ) f(x) f(x)在 D D D上二阶连续可微,如果 f ( x ) f(x) f(x)的Hessian矩阵在 D D D上半正定,则 f ( x ) f(x) f(x)是 D D D上的凸函数。
需证明 ∇ 2 E ( w , b ) \nabla^2E_{(w,b)} ∇2E(w,b)是半正定矩阵。
半正定矩阵的判定定理:若实对称矩阵的所有顺序主子式均为非负,则该矩阵是半正定。
顺序主子式:第1到第n阶行列式
D 1 D_1 D1: ∣ 2 Σ i = 1 m x i 2 ∣ > 0 |2\Sigma_{i=1}^mx_i^2|>0 ∣2Σi=1mxi2∣>0
D 2 D_2 D2: ∣ 2 Σ i = 1 m x i 2 2 Σ i = 1 m x i 2 Σ i = 1 m x i 2 m ∣ \left| \begin{array}{cccc} 2 \Sigma_{i=1}^mx_i^2 & 2 \Sigma_{i=1}^mx_i\\ 2 \Sigma_{i=1}^mx_i & 2m \end{array} \right| ∣ ∣2Σi=1mxi22Σi=1mxi2Σi=1mxi2m∣ ∣
求解 D 2 D_2 D2,利用 m × 1 m m\times\frac{1}{m} m×m1来构造 x ˉ \bar{x} xˉ,最终得到 4 m Σ i = 1 m ( x i − x ˉ ) 2 ≥ 0 4m\Sigma_{i=1}^m(x_i-\bar{x})^2\geq 0 4mΣi=1m(xi−xˉ)2≥0
即所有顺序主子式均为非负, ∇ 2 E ( w , b ) \nabla^2E_{(w,b)} ∇2E(w,b)是半正定矩阵得证, E ( w , b ) E_{(w,b)} E(w,b)是关于 w w w和 b b b的凸函数得证。
3.2.2求解损失函数的参数
因为 E ( w , b ) E_{(w,b)} E(w,b)是关于 w w w和 b b b的凸函数,所以根据凸充分性定理, ∇ E ( w , b ) = 0 \nabla E_{(w,b)}=0 ∇E(w,b)=0的点是最小值点。
令 ∂ E ( w , b ) ∂ b = 0 \frac{\partial E_{(w,b)}}{\partial b}=0 ∂b∂E(w,b)=0,得 b = 1 m Σ i = 1 m ( y i − w x i ) b=\frac{1}{m}\Sigma_{i=1}^m(y_i-wx_i) b=m1Σi=1m(yi−wxi)
为了便于求解 w w w,对 b b b化简, b = y ˉ − w x ˉ b=\bar{y}-w\bar{x} b=yˉ−wxˉ
令 ∂ E ( w , b ) ∂ w = 0 \frac{\partial E_{(w,b)}}{\partial w}=0 ∂w∂E(w,b)=0,得 w Σ i = 1 m x i 2 = Σ i = 1 m y i x i − Σ i = 1 m b x i w\Sigma_{i=1}^m x_i^2=\Sigma_{i=1}^m y_ix_i-\Sigma_{i=1}^mbx_i wΣi=1mxi2=Σi=1myixi−Σi=1mbxi
把 b = y ˉ − w x ˉ b=\bar{y}-w\bar{x} b=yˉ−wxˉ代入,移项求出 w w w,再进行变换,最终得到 w = Σ i = 1 m y i ( x i − x ˉ ) Σ i = 1 m x i 2 − 1 m ( Σ i = 1 m x i ) 2 w=\frac{\Sigma_{i=1}^my_i(x_i-\bar{x})}{\Sigma_{i=1}^mx_i^2-\frac{1}{m}(\Sigma_{i=1}^mx_i)^2} w=Σi=1mxi2−m1(Σi=1mxi)2Σi=1myi(xi−xˉ)
3.2.3向量化
始终把项目导向放在第一位,那么观察到 w w w中含有大量的求和运算,我们联想到实现中多层循环的复杂,因此考虑将其向量化。
主要思路:观察 ( x i − x ˉ ) (x_i-\bar{x}) (xi−xˉ)可以理解为去均值后的 x i x_i xi,那么构造类似的表达式,将上式变换为去均值后的 x x x与 y y y的表达式。
注重基础运算!
w = Σ i = 1 m ( x i − x ˉ ) ( y i − y ˉ ) Σ i = 1 m ( x i − x ˉ ) 2 = x ⃗ d T y ⃗ d x ⃗ d T x ⃗ d w=\frac{\Sigma_{i=1}^m(x_i-\bar{x})(y_i-\bar{y})}{\Sigma_{i=1}^m(x_i-\bar{x})^2}=\frac{\vec{x}_d^T\vec{y}_d}{\vec{x}_d^T\vec{x}_d} w=Σi=1m(xi−xˉ)2Σi=1m(xi−xˉ)(yi−yˉ)=xdTxdxdTyd
3.2.4 多元线性回归
将 w \bold{w} w和 b b b组合成 w ^ \hat{\bold{w}} w^,得到线性模型 f ( x ^ i ) = w ^ T x ^ i f(\bold{\hat{x}_i})=\bold{\hat{w}^T}\bold{\hat{x}_i} f(x^i)=w^Tx^i
由最小二乘法得 E w ^ = ( y − X w ^ ) T ( y − X w ^ ) E_{\hat{\bold{w}}}=(\bold{y}-\bold{X\hat{w}})^T(\bold{y}-\bold{X\hat{w}}) Ew^=(y−Xw^)T(y−Xw^)
证明半正定,对损失函数求Hessian矩阵。
3.2.5 矩阵微分
再求Hessian 矩阵
∇ 2 E w ^ = 2 X T X \nabla^2E_{\bold{\hat{w}}}=2\bold{X}^T\bold{X} ∇2Ew^=2XTX
假设 X T X \bold{X}^T\bold{X} XTX为满秩矩阵或正定矩阵,那么凸函数得证。对一阶偏导取零,求得 w ^ ∗ = ( X T X ) − 1 X T y \bold{\hat{w}}^*=(\bold{X}^T\bold{X})^{-1}\bold{X}^T\bold{y} w^∗=(XTX)−1XTy
现实情况中,由于特征数会超过样例数,此时的 X T X \bold{X}^T\bold{X} XTX不是满秩矩阵,则需引入正则化项。
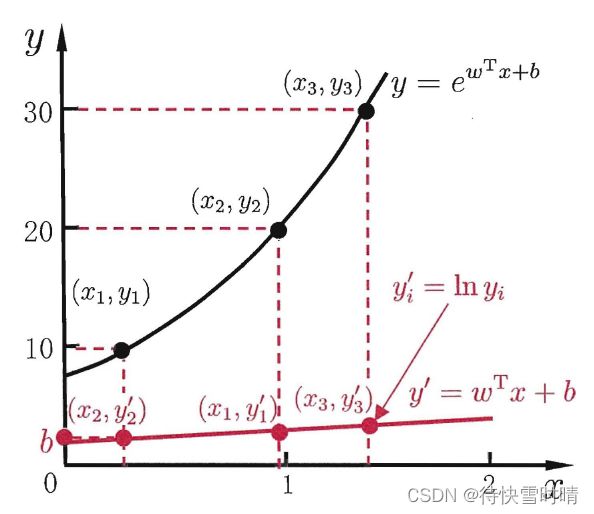
3.2.6 对数线性回归
ln y = w T x + b \ln y = \bold{w}^T\bold{x}+b lny=wTx+b
上式在形式上是线性回归,实质上是求取非线性函数映射。
根据演绎法推演到一般情况,考虑单调可微函数 g ( . ) g(.) g(.),令 y = g − 1 ( w T x + b ) y=g^{-1}(\bold{w}^T\bold{x}+b) y=g−1(wTx+b),称其为广义线性模型, g ( . ) g(.) g(.)为联系函数。
3.3 Logistic 回归 (解决分类问题)
考虑分类任务,我们使用3.2.6中提到的联系函数,来把分类任务中的真实标记 y y y和线性回归模型的预测值联系起来。
机器学习三要素
- 模型:线性模型,输出 ∈ { 0 , 1 } \in\{0,1\} ∈{0,1},近似阶跃的单调可微函数
- 策略:极大似然估计,信息论
- 算法:梯度下降,牛顿法
3.3.1 联系函数
- 单位阶跃函数(unit-step function)
该函数可以把实值 z z z转换为0/1值。
缺点 :不连续,不能直接取反函数。
-
对数几率函数(logistic function)
y = 1 1 + e − z y=\frac{1}{1+e^{-z}} y=1+e−z1 一种Sigmoid函数(S型)
令 z = w T x + b z=\bold{w}^T\bold{x}+b z=wTx+b,则 y = 1 1 + e − ( w T x + b ) y=\frac{1}{1+e^{-(\bold{w}^T\bold{x}+b)}} y=1+e−(wTx+b)1
两边取对数,可得 ln y 1 − y = w T x + b \ln \frac{y}{1-y}=\bold{w}^T\bold{x}+b ln1−yy=wTx+b
其中,令 y = p ( y = 1 ∣ x ) y=p(y=1|x) y=p(y=1∣x),则 1 − y = p ( y = 0 ∣ x ) 1-y = p(y=0|x) 1−y=p(y=0∣x),那么 y 1 − y \frac{y}{1-y} 1−yy称为 几率(odds),反映了 x x x作为正例的相对可能性。对几率取对数,则得到对数几率(logit)。
掌握模型输出的含义: y = p ( y = 1 ∣ x ) y=p(y=1|x) y=p(y=1∣x),给定一个样本 x x x,输出 y = 1 y=1 y=1的可能性。
优点 :
-
直接建模,无需假设数据分布;
-
得到近似概率预测,可以辅助决策;
-
任意阶可导的凸函数,可求取最优解。
3.3.2 参数估计
使用数值优化算法,如:梯度下降、牛顿法得到损失函数的最优解 β ∗ = arg min β l ( β ) \beta^*=\arg\min_\beta l(\beta) β∗=argminβl(β),这里的最优解不是闭式解,而是近似解。
3.3.2.1 极大似然估计
-
确定概率质量函数
预测值 y ∈ { 0 , 1 } y \in \{0,1\} y∈{0,1}取值为1和0的概率分别为
p ( y = 1 ∣ x ) = 1 1 + e − ( w T x + b ) = e w T x + b 1 + e w T x + b p(y=1|x)=\frac{1}{1+e^{-(\bold{w}^T\bold{x}+b)}}=\frac{e^{\bold{w}^T\bold{x}+b}}{1+e^{\bold{w}^T\bold{x}+b}} p(y=1∣x)=1+e−(wTx+b)1=1+ewTx+bewTx+b
p ( y = 0 ∣ x ) = 1 − p ( y = 1 ∣ x ) = 1 1 + e ( w T x + b ) p(y=0|x)=1-p(y=1|x)=\frac{1}{1+e^{(\bold{w}^T\bold{x}+b)}} p(y=0∣x)=1−p(y=1∣x)=1+e(wTx+b)1
为便于讨论,令 β = ( w ; b ) \bold{\beta}=(\bold{w};b) β=(w;b), x ^ = ( x ; 1 ) \hat{\bold{x}}=(\bold{x};1) x^=(x;1),则上式简写为
p ( y = 1 ∣ x ^ ; β ) = e β T x ^ 1 + e β T x ^ = p 1 ( x ^ ; β ) p(y=1|\hat{\bold{x}};\bold{\beta})=\frac{e^{\bold{\beta}^T\hat{\bold{x}}}}{1+e^{\bold{\beta}^T\hat{\bold{x}}}}=p_1(\hat{\bold{x}};\bold{\beta}) p(y=1∣x^;β)=1+eβTx^eβTx^=p1(x^;β)
p ( y = 0 ∣ x ^ ; β ) = 1 1 + e β T x ^ = p 0 ( x ^ ; β ) p(y=0|\hat{\bold{x}};\bold{\beta})=\frac{1}{1+e^{\bold{\beta}^T\hat{\bold{x}}}}=p_0(\hat{\bold{x}};\bold{\beta}) p(y=0∣x^;β)=1+eβTx^1=p0(x^;β)
合并后写成 p ( y ∣ x ^ ; β ) = y × p 1 ( x ^ ; β ) + ( 1 − y ) × p 0 ( x ^ ; β ) p(y|\hat{\bold{x}};\bold{\beta})=y\times p_1(\hat{\bold{x}};\bold{\beta})+(1-y)\times p_0(\hat{\bold{x}};\bold{\beta}) p(y∣x^;β)=y×p1(x^;β)+(1−y)×p0(x^;β)
-
写出似然函数
L ( β ) = ∏ i = 1 m p ( y i ∣ x ^ i ; β ) L(\bold{\beta})=\prod_{i=1}^mp(y_i|\hat{\bold{x}}_i;\bold{\beta}) L(β)=∏i=1mp(yi∣x^i;β)
对数似然函数是
l ( β ) = ln L ( β ) = Σ i = 1 m ln p ( y i ∣ x ^ i ; β ) = Σ i = 1 m ln ( y × p 1 ( x ^ i ; β ) + ( 1 − y ) × p 0 ( x ^ i ; β ) ) l(\bold{\beta})=\ln L(\bold{\beta})=\Sigma_{i=1}^m \ln p(y_i|\hat{\bold{x}}_i;\bold{\beta})=\Sigma_{i=1}^m \ln(y\times p_1(\hat{\bold{x}}_i;\bold{\beta})+(1-y)\times p_0(\hat{\bold{x}}_i;\bold{\beta})) l(β)=lnL(β)=Σi=1mlnp(yi∣x^i;β)=Σi=1mln(y×p1(x^i;β)+(1−y)×p0(x^i;β))
将 p 1 ( x ^ i ; β ) = e β T x ^ i 1 + e β T x ^ i p_1(\hat{\bold{x}}_i;\bold{\beta})=\frac{e^{\bold{\beta}^T\hat{\bold{x}}_i}}{1+e^{\bold{\beta}^T\hat{\bold{x}}_i}} p1(x^i;β)=1+eβTx^ieβTx^i, p 0 ( x ^ i ; β ) = 1 1 + e β T x ^ i p_0(\hat{\bold{x}}_i;\bold{\beta})=\frac{1}{1+e^{\bold{\beta}^T\hat{\bold{x}}_i}} p0(x^i;β)=1+eβTx^i1代入,得到
l ( β ) = Σ i = 1 m ( ln ( y i e β T x ^ i + 1 − y i ) − ln ( 1 + e β T x ^ i ) ) l(\bold{\beta})=\Sigma_{i=1}^m(\ln(y_ie^{\bold{\beta}^T\hat{\bold{x}}_i}+1-y_i)-\ln(1+e^{\bold{\beta}^T\hat{\bold{x}}_i})) l(β)=Σi=1m(ln(yieβTx^i+1−yi)−ln(1+eβTx^i))
因为 y i ∈ { 0 , 1 } y_i \in \{0,1\} yi∈{0,1}
分类讨论 y i = 0 y_i=0 yi=0和 y i = 1 y_i=1 yi=1的情况,综合可得 l ( β ) = Σ i = 1 m ( y i β T x ^ i − ln ( 1 + e β T x ^ i ) ) l(\bold{\beta})=\Sigma_{i=1}^m(y_i\bold{\beta}^T\hat{\bold{x}}_i-\ln(1+e^{\bold{\beta}^T\hat{\bold{x}}_i})) l(β)=Σi=1m(yiβTx^i−ln(1+eβTx^i))
此时最大化 l ( β ) l(\bold{\beta}) l(β)即为最小化相反数 − l ( β ) -l(\bold{\beta}) −l(β)。
3.3.2.2 信息熵
自信息
I ( X ) = − log b p ( x ) I(X)=-\log_bp(x) I(X)=−logbp(x)
信息熵
度量随机变量X的不确定性,信息熵越大越不确定。
H ( X ) = E [ I ( X ) ] = − Σ x p ( x ) log b p ( x ) H(X)=E[I(X)]=-\Sigma_xp(x)\log_bp(x) H(X)=E[I(X)]=−Σxp(x)logbp(x)
约定:若 p ( x ) = 0 p(x)=0 p(x)=0,则 p ( x ) log b p ( x ) = 0 p(x)\log_bp(x)=0 p(x)logbp(x)=0
相对熵(KL散度)
度量两个分布的差异,用于度量理想分布 p ( x ) p(x) p(x)和模拟分布 q ( x ) q(x) q(x)之间的差异。
D K L ( p ∣ ∣ q ) = Σ x p ( x ) log b ( p ( x ) q ( x ) ) = Σ x p ( x ) log b p ( x ) − Σ x p ( x ) log b q ( x ) D_{KL}(p||q)=\Sigma_xp(x)\log_b(\frac{p(x)}{q(x)})=\Sigma_xp(x)\log_bp(x)-\Sigma_xp(x)\log_bq(x) DKL(p∣∣q)=Σxp(x)logb(q(x)p(x))=Σxp(x)logbp(x)−Σxp(x)logbq(x)
其中 − Σ x p ( x ) log b q ( x ) -\Sigma_xp(x)\log_bq(x) −Σxp(x)logbq(x)称为交叉熵。
最小化相对熵,可以令 q ( x ) q(x) q(x)接近 p ( x ) p(x) p(x),即求出最优分布。从频率学派的角度看, p ( x ) p(x) p(x)是固定的, Σ x p ( x ) log b p ( x ) \Sigma_xp(x)\log_bp(x) Σxp(x)logbp(x)当作常量,因此最小化相对熵,就是最小化交叉熵 − Σ x p ( x ) log b q ( x ) -\Sigma_xp(x)\log_bq(x) −Σxp(x)logbq(x)。
- 列出理想分布 p ( x ) p(x) p(x)和模拟分布 q ( x ) q(x) q(x)
-
写出交叉熵
-
单个样本 y i y_i yi的交叉熵
− Σ y i p ( y i ) log b q ( y i ) = − p ( 1 ) × log b p 1 ( x ^ ; β ) − p ( 0 ) × log b p 0 ( x ^ ; β ) = − y i × log b p 1 ( x ^ ; β ) − ( 1 − y i ) × log b p 0 ( x ^ ; β ) -\Sigma_{y_i}p(y_i)\log_bq(y_i)=-p(1)\times\log_bp_1(\hat{\bold{x}};\bold{\beta})-p(0)\times\log_bp_0(\hat{\bold{x}};\bold{\beta})=-y_i\times\log_bp_1(\hat{\bold{x}};\bold{\beta})-(1-y_i)\times\log_bp_0(\hat{\bold{x}};\bold{\beta}) −Σyip(yi)logbq(yi)=−p(1)×logbp1(x^;β)−p(0)×logbp0(x^;β)=−yi×logbp1(x^;β)−(1−yi)×logbp0(x^;β)
令 b = e b=e b=e,上式为
− y i × ln p 1 ( x ^ ; β ) − ( 1 − y i ) × ln p 0 ( x ^ ; β ) -y_i\times\ln p_1(\hat{\bold{x}};\bold{\beta})-(1-y_i)\times\ln p_0(\hat{\bold{x}};\bold{\beta}) −yi×lnp1(x^;β)−(1−yi)×lnp0(x^;β)
-
全体样本的交叉熵
Σ i = 1 m [ − y i × ln p 1 ( x ^ i ; β ) − ( 1 − y i ) × ln p 0 ( x ^ i ; β ) ] \Sigma_{i=1}^m[-y_i\times\ln p_1(\hat{\bold{x}}_i;\bold{\beta})-(1-y_i)\times\ln p_0(\hat{\bold{x}}_i;\bold{\beta})] Σi=1m[−yi×lnp1(x^i;β)−(1−yi)×lnp0(x^i;β)]
化简后得到
Σ i = 1 m [ − y i ln ( e β T x ^ i ) − ln ( 1 1 + e β T x ^ i ) ] = Σ i = 1 m ( − y i β T x ^ i + ln ( 1 + e β T x ^ i ) ) \Sigma_{i=1}^m[-y_i\ln(e^{\beta^T\hat{x}_i})-\ln(\frac{1}{1+e^{\beta^T\hat{x}_i}})]=\Sigma_{i=1}^m(-y_i\bold{\beta}^T\hat{\bold{x}}_i+\ln(1+e^{\bold{\beta}^T\hat{\bold{x}}_i})) Σi=1m[−yiln(eβTx^i)−ln(1+eβTx^i1)]=Σi=1m(−yiβTx^i+ln(1+eβTx^i))
与极大似然估计得到的 − l ( β ) -l(\beta) −l(β)殊途同归
-
3.4 线性判别分析
Linear Discriminant Analysis,简称LDA
从几何角度来看,全体训练样本经过投影后:
-
异类样本的中心尽可能远
二范数:求向量的模长 max ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 \max ||\bold{w}^T\bold{\mu}_0-\bold{w}^T\bold{\mu}_1||_2^2 max∣∣wTμ0−wTμ1∣∣22
由于直接算投影长度不好操作,因此我们计算 w w w和 μ \mu μ的内积,如 w T μ 0 \bold{w}^T\bold{\mu}_0 wTμ0,计算简便。已知 w w w的模长不影响正负类样本的中心距离,因此我们通过在正负类样本中心 ∣ μ 1 ∣ cos θ 1 |\bold{\mu}_1|\cos\theta_1 ∣μ1∣cosθ1和 ∣ μ 0 ∣ cos θ 0 |\bold{\mu}_0|\cos\theta_0 ∣μ0∣cosθ0乘以一个模长 ∣ ∣ w ∣ ∣ ||\bold{w}|| ∣∣w∣∣,来得到内积的形式 w T μ 0 = ∣ ∣ w ∣ ∣ × ∣ μ 0 ∣ cos θ 0 \bold{w}^T\bold{\mu}_0=||\bold{w}||\times |\bold{\mu}_0|\cos\theta_0 wTμ0=∣∣w∣∣×∣μ0∣cosθ0,实现计算的简化。
-
同类样本的方差尽可能小
此处的方差并非严格方差。
min w T Σ 0 w + w T Σ 1 w \min \bold{w}^T\bold{\Sigma}_0\bold{w}+\bold{w}^T\bold{\Sigma}_1\bold{w} minwTΣ0w+wTΣ1w
w T Σ 0 w = w T ( Σ x ∈ X 0 ( x − μ 0 ) ( x − μ 0 ) T ) w \bold{w}^T\bold{\Sigma}_0\bold{w}=\bold{w}^T(\Sigma_{x\in X_0}(\bold{x}-\bold{\mu}_0)(\bold{x}-\bold{\mu}_0)^T)\bold{w} wTΣ0w=wT(Σx∈X0(x−μ0)(x−μ0)T)w
-
损失函数推导
max J = ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 w T Σ 0 w + w T Σ 1 w = ∣ ∣ ( μ 0 − μ 1 ) T w ∣ ∣ 2 2 w T ( Σ 0 + Σ 1 ) w = [ ( μ 0 − μ 1 ) T w ] T ( μ 0 − μ 1 ) T w w T ( Σ 0 + Σ 1 ) w = w T ( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w w T ( Σ 0 + Σ 1 ) w \max J=\frac{||\bold{w}^T\bold{\mu}_0-\bold{w}^T\bold{\mu}_1||_2^2}{\bold{w}^T\bold{\Sigma}_0\bold{w}+\bold{w}^T\bold{\Sigma}_1\bold{w}}=\frac{||(\bold{\mu}_0-\bold{\mu}_1)^T\bold{w}||_2^2}{\bold{w}^T(\bold{\Sigma}_0+\bold{\Sigma}_1)\bold{w}}=\frac{[(\bold{\mu}_0-\bold{\mu}_1)^T\bold{w}]^T (\bold{\mu}_0-\bold{\mu}_1)^T\bold{w}}{\bold{w}^T(\bold{\Sigma}_0+\bold{\Sigma}_1)\bold{w}}=\frac{\bold{w}^T(\bold{\mu}_0-\bold{\mu}_1)(\bold{\mu}_0-\bold{\mu}_1)^T\bold{w}}{\bold{w}^T(\bold{\Sigma}_0+\bold{\Sigma}_1)\bold{w}} maxJ=wTΣ0w+wTΣ1w∣∣wTμ0−wTμ1∣∣22=wT(Σ0+Σ1)w∣∣(μ0−μ1)Tw∣∣22=wT(Σ0+Σ1)w[(μ0−μ1)Tw]T(μ0−μ1)Tw=wT(Σ0+Σ1)wwT(μ0−μ1)(μ0−μ1)Tw
max J = w T S b w w T S w w \max J=\frac{\bold{w^T\bold{S}_b\bold{w}}}{\bold{w^T\bold{S}_w\bold{w}}} maxJ=wTSwwwTSbw
目标问题:
min w − w T S b w \min _w -\bold{w^T\bold{S}_b\bold{w}} minw−wTSbw
s.t. w T S w w = 1 \bold{w^T\bold{S}_w\bold{w}}=1 wTSww=1
一旦把分母固定化,则可以求解这个最优化问题。
使用拉格朗日乘子法,求出局部极值点,这里的目标函数 − w T S b w = − ∣ ∣ w T μ 0 − w T μ 1 ∣ ∣ 2 2 ≤ 0 -\bold{w^T\bold{S}_b\bold{w}}=-||\bold{w}^T\bold{\mu}_0-\bold{w}^T\bold{\mu}_1||_2^2\leq0 −wTSbw=−∣∣wTμ0−wTμ1∣∣22≤0,所以最大值为0。又因为异类样本的中心在几何角度看一定存在最值距离,所以一定存在最小值。
-
求解 w w w
min w − w T S b w \min _w -\bold{w^T\bold{S}_b\bold{w}} minw−wTSbw
s.t. w T S w w = 1 \bold{w^T\bold{S}_w\bold{w}}=1 wTSww=1 -> w T S w w − 1 = 0 \bold{w^T\bold{S}_w\bold{w}}-1=0 wTSww−1=0
拉格朗日函数为
L ( w , λ ) = − w T S b w + λ ( w T S w w − 1 ) L(\bold{w},\lambda)=-\bold{w^T\bold{S}_b\bold{w}}+\lambda(\bold{w^T\bold{S}_w\bold{w}}-1) L(w,λ)=−wTSbw+λ(wTSww−1)
对 w w w求偏导
∂ L ( w , λ ) ∂ w = − ( S b + S b T ) w + λ ( S w + S w T ) w \frac{\partial L(\bold{w},\lambda)}{\partial \bold{w}}=-(\bold{S}_b+\bold{S}_b^T)\bold{w}+\lambda(\bold{S}_w+\bold{S}_w^T)\bold{w} ∂w∂L(w,λ)=−(Sb+SbT)w+λ(Sw+SwT)w
因为 S b S_b Sb和 S w S_w Sw是对称阵,所以 ∂ L ( w , λ ) ∂ w = − 2 S b w + 2 λ S w w \frac{\partial L(\bold{w},\lambda)}{\partial \bold{w}}=-2\bold{S}_b\bold{w}+2\lambda\bold{S}_w\bold{w} ∂w∂L(w,λ)=−2Sbw+2λSww
令上式等于0,得到 S b w = λ S w w \bold{S}_b\bold{w}=\lambda\bold{S}_w\bold{w} Sbw=λSww
即求广义特征值问题。
( μ 0 − μ 1 ) ( μ 0 − μ 1 ) T w = λ S w w (\bold{\mu}_0-\bold{\mu}_1)(\bold{\mu}_0-\bold{\mu}_1)^T\bold{w}=\lambda\bold{S}_w\bold{w} (μ0−μ1)(μ0−μ1)Tw=λSww
令 ( μ 0 − μ 1 ) T w = γ (\bold{\mu}_0-\bold{\mu}_1)^T\bold{w}=\gamma (μ0−μ1)Tw=γ,则 γ ( μ 0 − μ 1 ) w = λ S w w \gamma(\bold{\mu}_0-\bold{\mu}_1)\bold{w}=\lambda\bold{S}_w\bold{w} γ(μ0−μ1)w=λSww
得 w = γ λ S w − 1 ( μ 0 − μ 1 ) \bold{w}=\frac{\gamma}{\lambda}\bold{S}_w^{-1}(\bold{\mu}_0-\bold{\mu}_1) w=λγSw−1(μ0−μ1)
最终求解的 w \bold{w} w不关心其大小,只关心其方向,所以常数项 γ λ \frac{\gamma}{\lambda} λγ可以任意取值,若取1,则得到公式(3.39)。
广义特征值
广义瑞利商
实数域中,厄米等于转置。
性质: