【机器学习】李宏毅 - 04 深度学习介绍和反向传播机制
文章目录
- 深度学习
- 深度学习发展历程
- 深度学习步骤
-
- 1. 神经网络
-
- 基本结构
- 完全连接前馈神经网络(Fully Connet Feedforward Network)
- 矩阵运算
- 案例:手写数字识别
- 2. 模型评估
- 3. 选择最优参数
- 反向传播(Backpropagation)
-
- 计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z的部分称为 前向(Forward pass)
- 计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C的部分称为 反向(Backward pass)
- 情况1:假设红色神经元在最后一个隐藏层
- 情况2: 假设红色神经元不在最后一个隐藏层中
- 链式法则
- 普遍性定理
深度学习
Neural Network 神经网络
- 每一排Neuron( a 1 , a 2 , a 3 a_1,a_2,a_3 a1,a2,a3)就叫一个hidden layer
- 多个hidden layer就叫deep learning
问题1: 为什么要deep而不fat?
问题2: 为什么我们不继续“deep”呢?
警惕过拟合!(在训练资料上变好,但是在未知数据资料上预测不佳)
深度学习发展历程
-
Perceptron
Perceptron很像我们的逻辑回归(Logistics Regression)只不过是没有sigmoid激活函数。09年的GPU的发展是很关键的,使用GPU矩阵运算节省了很多的时间。
But! Perceptron has limitation.
-
Multi-layer perceptron
similar to DNN
But! 1 hidden layer is good enough.
-
Backpropagation
-
RBM initialization (breakthrough)
-
GPU
-
Popular in speech recognition
-
Win in image competition
深度学习步骤
- Step1:神经网络(Neural network)
- Step2:模型评估(Goodness of function)
- Step3:选择最优函数(Pick the best function)
1. 神经网络
基本结构
神经网络中的节点,类似神经元。具体的连接方式需要手动设计。
前馈(Feedforward) :特点是单向信号流动,从前(输入层)往后(输出层)传,叫作前馈。
完全连接(Fully connect) :每一层之间所有的神经元(neuron)两两连接。
常见的多层结构前馈网络由三部分组成
输入层(Input layer) :众多神经元(Neuron)接受大量非线形输入消息。输入的消息称为输入向量。
隐藏层(Hidden layer) :Deep = Many hidden layers。 简称“隐层”,是输入层和输出层之间众多神经元和链接组成的各个层面。隐层可以有一层或多层。隐层的节点(神经元)数目不定,但数目越多神经网络的非线性越显著,从而神经网络的健壮性(Robustness)更显著。同样地,运算量也会增大,因此引入后面的矩阵运算(Matrix Operation)。
输出层(Output layer) :消息在神经元链接中传输、分析、权衡,形成输出结果。输出的消息称为输出向量。
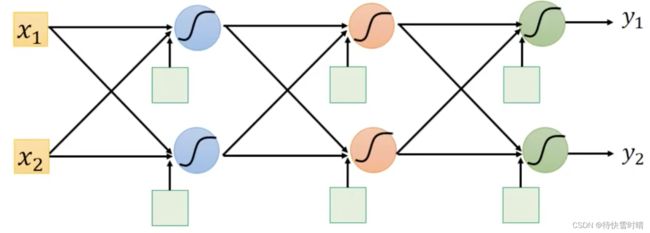
完全连接前馈神经网络(Fully Connet Feedforward Network)
如下图,当一个神经网络中的权重和偏差都已知,则可以看成一个函数,输入是一个向量,输出也是向量。
给定网络构造,不论是做回归模型(linear model)还是逻辑回归(logistics regression),当我们用不同的参数创建不同的函数时,形成了 函数集(a function set) 。函数集是比较大的,很难用以前的回归模型去涵盖,所以这是深度学习的优势。
这里的三部分组成结构是
- 输入层 Input layer : 1
- 隐藏层 Hidden layers : N
- 输出层 Output layer : 1
矩阵运算
嵌套运算,可以用GPU加速。
神经网络的本质:通过隐藏层进行特征转换

对于输出层,其实是把前面的隐藏层的输出当做输入(经过特征提取得到的一组最好的特征)然后通过一个多分类器(Multi-class classification problem)(可以是softmax函数)得到最后的输出y。
案例:手写数字识别
神经网络的结构决定了函数集function set。
Model Structure:自己设计决定几层layer,每个layer中多少个neuron。(如:CNN)
方法的转变:如何抽取feature → \rightarrow → design network structure
对于语音识别和影像识别,深度学习是个好的方法,因为特征工程提取特征并不容易。
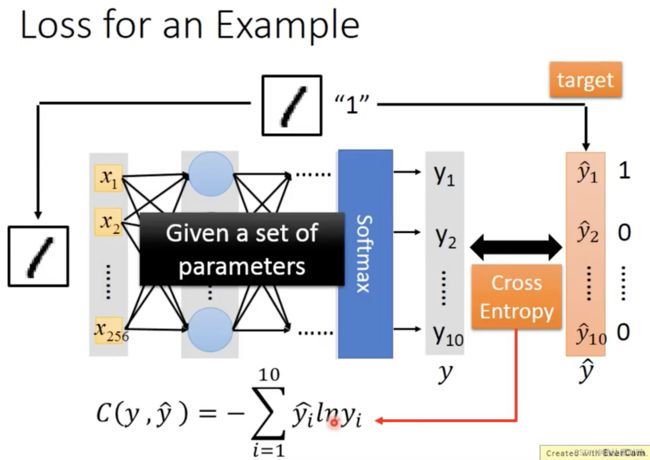
2. 模型评估
- 计算交叉熵,使之越小越好。
- 计算训练数据的总损失,从函数集中找最优函数,或找损失函数中的最优参数。
3. 选择最优参数
梯度下降。
反向传播(Backpropagation)
计算偏微分的有效方式,因为在神经网络中,计算偏微分向量含有大量的参数,因此效率是计算的重要性能度量。
这里需区分三种类型的损失函数。
损失函数(Loss function) 是定义在 单个训练样本 上的,也就是就算一个样本的误差,比如我们想要分类,就是预测的类别和实际类别的区别,是一个样本的,用L表示。
代价函数(Cost function) 是定义在 整个训练集 上面的,也就是所有样本的误差的总和的平均,也就是损失函数的总和的平均,有没有这个平均其实不会影响最后的参数的求解结果。
总体损失函数(Total loss function) 是定义在 整个训练集 上面的,也就是所有样本的误差的总和。也就是平时我们反向传播需要最小化的值。
方法:定义 总体损失函数 L ( θ ) = Σ n = 1 N C n ( θ ) L(\theta)=\Sigma_{n=1}^N C^n(\theta) L(θ)=Σn=1NCn(θ),再累加计算每一笔数据的损失 C n C^n Cn对 w w w的偏微分 ∂ L ( θ ) ∂ w = Σ n = 1 N ∂ C n ( θ ) ∂ w \frac{\partial L(\theta)}{\partial w}=\Sigma_{n=1}^N\frac{\partial C^n(\theta)}{\partial w} ∂w∂L(θ)=Σn=1N∂w∂Cn(θ),然后用梯度下降不断更新,得到损失最小的函数。
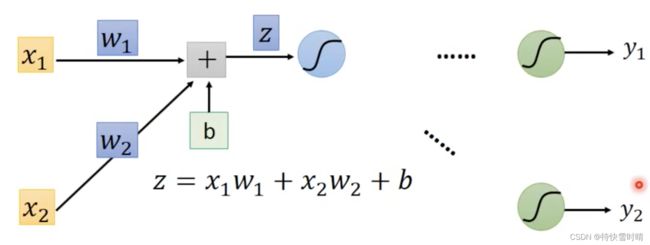
考虑神经网络中的某一个神经元:取第一层的神经元。
∂ C ∂ w = ∂ z ∂ w ∂ C ∂ z \frac{\partial C}{\partial w}=\frac{\partial z}{\partial w} \frac{\partial C}{\partial z} ∂w∂C=∂w∂z∂z∂C
-
计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z的部分称为 前向(Forward pass)
具体来看, ∂ z ∂ w 1 = x 1 \frac{\partial z}{\partial w_1}=x_1 ∂w1∂z=x1, ∂ z ∂ w 2 = x 2 \frac{\partial z}{\partial w_2}=x_2 ∂w2∂z=x2。规律是看 w w w前接的输入值是什么( x 1 x_1 x1, x 2 x_2 x2),微分后就是什么( x 1 x_1 x1, x 2 x_2 x2)。这一部分很简单,直接前向计算,每个神经元对应的输入就是所求值。

-
计算 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C的部分称为 反向(Backward pass)
这一部分比较复杂,利用链式法则对这一项做拆解。
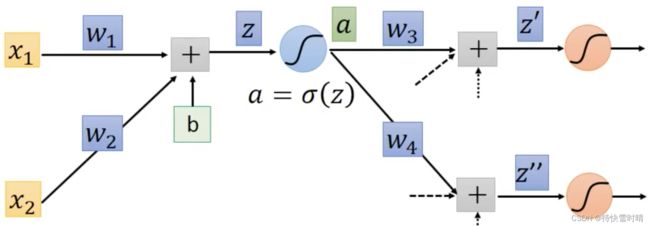
原式可以变为 ∂ C ∂ z = ∂ a ∂ z ∂ C ∂ a \frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a} ∂z∂C=∂z∂a∂a∂C
∂ a ∂ z = σ ′ ( z ) \frac{\partial a}{\partial z}=\sigma^{'}(z) ∂z∂a=σ′(z),从图像上直观来看,激活函数的微分如下所示。

假设第一个蓝色神经元的下一层,含有2个红色的神经元,则 a a a只影响两项 ∂ z ′ \partial z^{'} ∂z′ 和 ∂ z ′ ′ \partial z^{''} ∂z′′。
∂ C ∂ a = ∂ z ′ ∂ a ∂ C ∂ z ′ + ∂ z ′ ′ ∂ a ∂ C ∂ z ′ ′ \frac{\partial C}{\partial a}=\frac{\partial z^{'}}{\partial a}\frac{\partial C}{\partial z^{'}}+\frac{\partial z^{''}}{\partial a}\frac{\partial C}{\partial z^{''}} ∂a∂C=∂a∂z′∂z′∂C+∂a∂z′′∂z′′∂C (链式法则)
其中从图上可以直观看出 ∂ z ′ ∂ a = w 3 \frac{\partial z^{'}}{\partial a}=w_3 ∂a∂z′=w3, ∂ z ′ ′ ∂ a = w 4 \frac{\partial z^{''}}{\partial a}=w_4 ∂a∂z′′=w4。
现在假设我们能计算出 ∂ C ∂ z ′ \frac{\partial C}{\partial z^{'}} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z^{''}} ∂z′′∂C,那么可以直接带入算出 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C。
想象有另一个神经元(neuron)<三角形状>,不在我们原有的网络中,把前向的过程“逆向”,那么这个神经元的输入就是 ∂ C ∂ z ′ \frac{\partial C}{\partial z^{'}} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z^{''}} ∂z′′∂C,乘以权重,再通过激活函数,就得到了 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C。
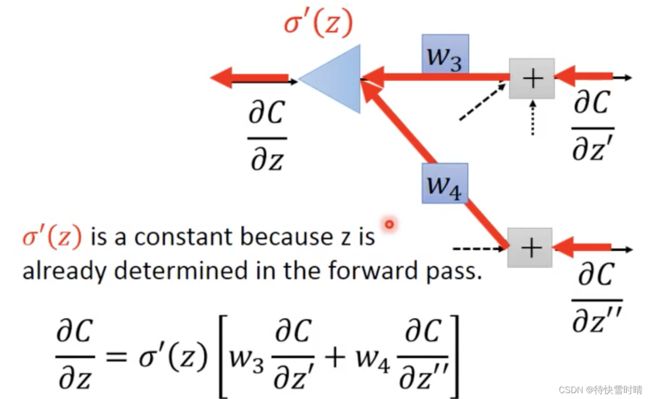
值得注意的是, z z z是一个已经固定的值,在计算Forward pass的时候就被决定好了,那么在给定 z z z的情况下 σ ′ ( z ) \sigma^{'}(z) σ′(z)是一个常数。
情况1:假设红色神经元在最后一个隐藏层
直接计算就能出结果。
∂ C ∂ z ′ = ∂ y 1 ∂ z ′ ∂ C ∂ y 1 \frac{\partial C}{\partial z^{'}}=\frac{\partial y_1}{\partial z^{'}}\frac{\partial C}{\partial y_1} ∂z′∂C=∂z′∂y1∂y1∂C
第一项根据激活函数计算;第二项根据损失函数,用交叉熵/均方误差来计算。
情况2: 假设红色神经元不在最后一个隐藏层中
先计算后面的偏微分,乘上权重,那么就得到前面的偏微分。如果都不知道,那么继续往后面层计算,一直到输出值,从输出值那里出发再反向计算。

实际上,从输出层开始算,运算量和原来的神经网络的前向传播的计算量一样。
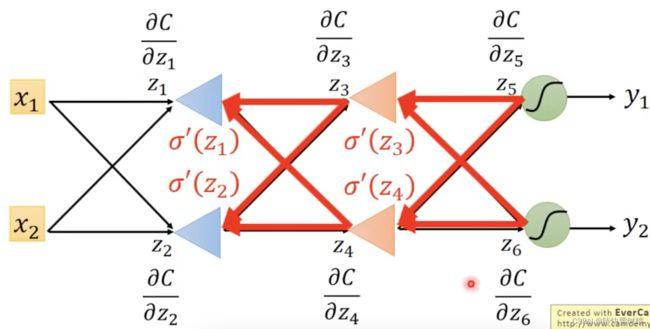
总结:首先做前向的计算,然后建立反向神经网络,从右向左,把输出层当作输入层,运算是一样的。
链式法则
情况1:
y = g ( x ) y=g(x) y=g(x) z = h ( y ) z=h(y) z=h(y)
d z d x = d z d y d y d x \frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx} dxdz=dydzdxdy
情况2:
x = g ( s ) x=g(s) x=g(s) y = h ( s ) y=h(s) y=h(s) z = k ( x , y ) z=k(x,y) z=k(x,y)
d z d s = ∂ z ∂ x d x d s + ∂ z ∂ y d y d s \frac{dz}{ds}=\frac{\partial z}{\partial x}\frac{dx}{ds}+\frac{\partial z}{\partial y}\frac{dy}{ds} dsdz=∂x∂zdsdx+∂y∂zdsdy
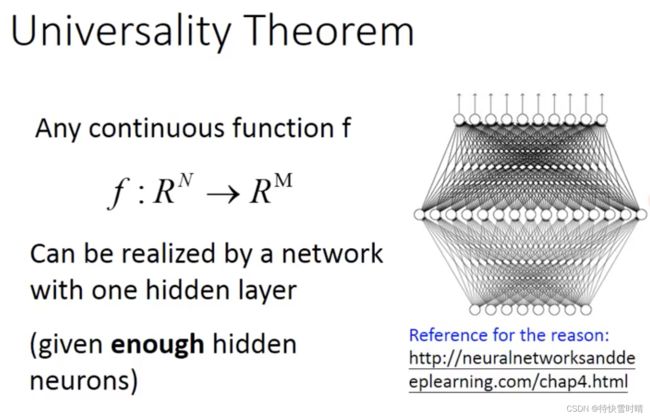
普遍性定理
总结:
One layer contains large amount of parameters ao that the performance is better.
为什么要Deep Learning?
Deep but not fat!