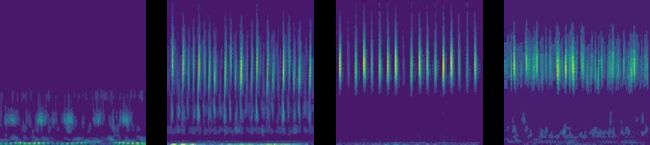
西储大学轴承数据小波变换

现在将一维数据转换为图片的做法也是五花八门，小波变换是最常见的，但是也有不少其他办法。其实思路都是差不多的，都是用一种编码方法把一位数据映射到二维空间，以图片的形式进行表示。除小波变换外，还有格拉米角场 GAFs、马尔可夫变迁场 MTF、递归图 、短时傅里叶变换STFT，具体原理大家在其他地方都能很方便的找到，我这儿就不放了，我自己掌握的也有限，只是把相关方法展示出来，供大家参考。今天时间有限，还是先把小波的放出来吧。

小波变换中可以有各种各样的小波类型可选，每种生成的图都是不一样的。

print(pywt.wavelist())

['bior1.1', 'bior1.3', 'bior1.5', 'bior2.2', 'bior2.4', 'bior2.6', 'bior2.8', 'bior3.1', 'bior3.3', 'bior3.5', 'bior3.7', 'bior3.9', 'bior4.4', 'bior5.5', 'bior6.8', 'cgau1', 'cgau2', 'cgau3', 'cgau4', 'cgau5', 'cgau6', 'cgau7', 'cgau8', 'cmor', 'coif1', 'coif2', 'coif3', 'coif4', 'coif5', 'coif6', 'coif7', 'coif8', 'coif9', 'coif10', 'coif11', 'coif12', 'coif13', 'coif14', 'coif15', 'coif16', 'coif17', 'db1', 'db2', 'db3', 'db4', 'db5', 'db6', 'db7', 'db8', 'db9', 'db10', 'db11', 'db12', 'db13', 'db14', 'db15', 'db16', 'db17', 'db18', 'db19', 'db20', 'db21', 'db22', 'db23', 'db24', 'db25', 'db26', 'db27', 'db28', 'db29', 'db30', 'db31', 'db32', 'db33', 'db34', 'db35', 'db36', 'db37', 'db38', 'dmey', 'fbsp', 'gaus1', 'gaus2', 'gaus3', 'gaus4', 'gaus5', 'gaus6', 'gaus7', 'gaus8', 'haar', 'mexh', 'morl', 'rbio1.1', 'rbio1.3', 'rbio1.5', 'rbio2.2', 'rbio2.4', 'rbio2.6', 'rbio2.8', 'rbio3.1', 'rbio3.3', 'rbio3.5', 'rbio3.7', 'rbio3.9', 'rbio4.4', 'rbio5.5', 'rbio6.8', 'shan', 'sym2', 'sym3', 'sym4', 'sym5', 'sym6', 'sym7', 'sym8', 'sym9', 'sym10', 'sym11', 'sym12', 'sym13', 'sym14', 'sym15', 'sym16', 'sym17', 'sym18', 'sym19', 'sym20']

我这里只展示其中一种morl小波，好像用这个的比较多。函数代码如下：

def show_cwt(data,i):
    t = np.arange(0, 2048 / 12000, 1.0 / 12000)
    wavename = 'morl'  
    totalscal = 256  # scale
    fc = pywt.central_frequency(wavename)  # central frequency
    cparam = 2 * fc * totalscal
    scales = cparam / np.arange(1, totalscal + 1)
    [cwtmatr_l, frequencies_l] = pywt.cwt(data, scales, wavename, 1.0 / 12000)  # continuous wavelet transform

    plt.figure(figsize=(5, 4))
    plt.contourf(t, frequencies_l, abs(cwtmatr_l), cmap='jet', levels=np.linspace(0, 1.2, 40), extend='both')
    # plt.contourf(t, frequencies_l, abs(cwtmatr_l), levels=np.linspace(0, 1.2, 40), extend='both')
    # plt.contourf(t, frequencies_l, abs(cwtmatr_l))
    plt.ylabel(u"Frequency [Hz]")
    plt.xlabel(u"Time [sec]")
    plt.axis('off')  # 不显示坐标轴及边框
    plt.savefig('test%.f.png'%(i), bbox_inches='tight', pad_inches=-0.1)  # 保存图像不显示白色边框
    plt.colorbar()
    plt.show()

生成的系列图片如下：

​从左到右依次是正常、内圈、外圈和滚动体故障

如果你在别的地方看到的图片不太一样，可能是小波种类的原因，或者cmap也就是色彩模式的设置以及levels=np.linspace的设置不一样，也就是说plt.contourf对于最终图像的表现形式影响比较大，大家可以自行测试。至于对最终的结果有多大影响，我个人还没有测试，后续我会再写。

今天先写到这里，下一章将写其他几种转换为图片的方法。