并行计算基础知识
并行计算基础知识
- 前言
- 并行计算的存在意义
- 并行计算中的计算(以用并行计算实现最小二乘回归的梯度下降为例)
- 并行计算中的通信
-
- 两种通信机制
-
- 共享内存(Share Memory)
- 消息传递(Massage Passing)
- 通信架构
-
- Client-Server Architecture
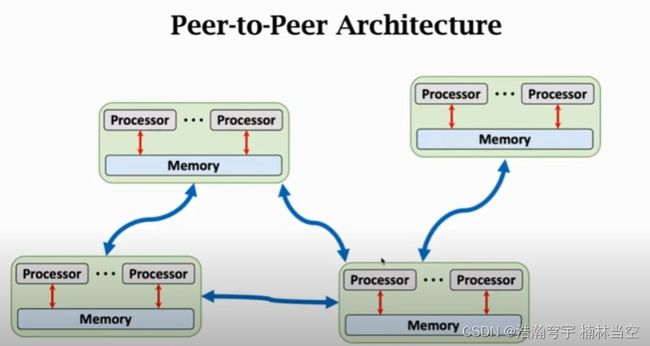
- Peer-to-Peer Architecture
- 用mapreduce实现client-server架构
- 通信对于整体效率的影响
-
- 网络通信代价的来源
-
- 通信复杂度(Communication Complexity)
-
- 定义
- 影响
- 延迟(Latency)
- 总结
- 同步时延
前言
这是王树森老师在YouTube上的机器学习视频的学习笔记,原视频通俗易懂,条理清晰。这里做简单记录,感兴趣者请移步王树森老师YouTube频道
频道链接:YouTube频道
视频链接:视频链接
本文主要总结了并行计算的基础知识,包括并行计算的存在意义、并行计算的计算过程与通信机制、通信对于并行计算效率的影响等问题。
并行计算的存在意义
机器学习的数据和网络规模巨大导致计算时间过长,并行计算用空间换时间,用多节点同时工作的方式减少Clock Time(但不减少CPU Time)。
并行计算由计算(Computation)和通信(Communication)两部分组成。计算即各个节点基于本地数据计算得到的参数值,通信即不同节点之间消息的传递。
并行计算中的计算(以用并行计算实现最小二乘回归的梯度下降为例)
对于最小二乘回归问题,我们希望基于样本 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi)训练得到参数 w \boldsymbol{w} w以使得实现从未标记数据 x \boldsymbol{x} x到其样本 y y y的预测。已知该问题的损失函数为 L ( w ) = ∑ i = 1 n 1 2 ( x i T w − y i ) 2 . (1) L(\boldsymbol{w})=\sum_{i=1}^n\frac{1}{2}\left(\boldsymbol{x}_i^{\mathrm{T}}\boldsymbol{w}-y_i\right)^2. \tag{1} L(w)=i=1∑n21(xiTw−yi)2.(1)
如果用梯度下降法求解该问题,则每一步梯度计算如下: g ( w ) = ∂ L ( w ) ∂ w = ∑ i = 1 n ( x i T w − y i ) x i = ∑ i = 1 n g i ( w ) . (2) \boldsymbol{g}(\boldsymbol{w})=\frac{\partial L(\boldsymbol{w})}{\partial \boldsymbol{w}}=\sum_{i=1}^n\left(\boldsymbol{x}_i^{\mathrm{T}}\boldsymbol{w}-y_i\right)\boldsymbol{x}_i=\sum_{i=1}^n \boldsymbol{g}_i(\boldsymbol{w}). \tag{2} g(w)=∂w∂L(w)=i=1∑n(xiTw−yi)xi=i=1∑ngi(w).(2)
可以看出,梯度向量可以被拆分成为子函数 { g i ( w ) } \left\{\boldsymbol{g}_i(\boldsymbol{w})\right\} {gi(w)}的求和,而各个子函数至于当前参数 w \boldsymbol{w} w以及本地数据 ( x i , y i ) (\boldsymbol{x}_i,y_i) (xi,yi)有关,与其他数据无关,因此可以设置 n n n个计算节点(worker nodes)并行计算,之后将各自的参数传到服务节点(server node)进行求和,即可得到整体的梯度向量。
由此可以看出,并行计算中的计算环节比较简单,而值得讨论的是“通信环节”。
并行计算中的通信
两种通信机制
共享内存(Share Memory)
各个节点之间数据共享,每个节点都知道所有节点的数据以及信息。
消息传递(Massage Passing)
不同节点之间数据不共享,各自用本地数据进行计算之后彼此之间只做massage的传递。消息传递机制应用较广,因此下面主要讨论该机制。
通信架构
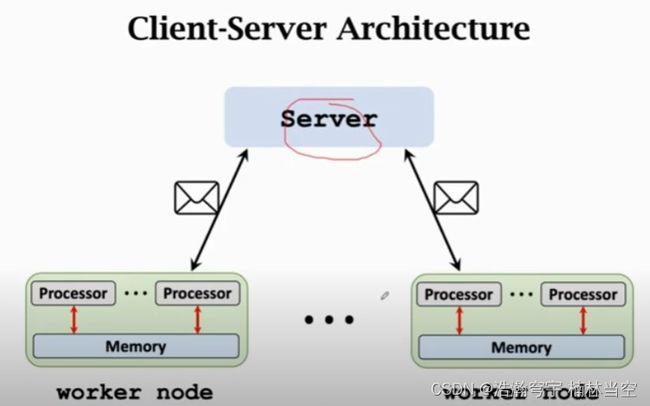
Client-Server Architecture
一个节点作为Server,专注统筹,其他节点做Worker,专职计算。
Peer-to-Peer Architecture
用mapreduce实现client-server架构
具体步骤:
- Broadcast: Server节点将当前参数广播给所有Workers;
- Map: 所有的Worker用本地数据算梯度;
- Reduce: Workers把结果传回Server节点进行整合;
通信对于整体效率的影响
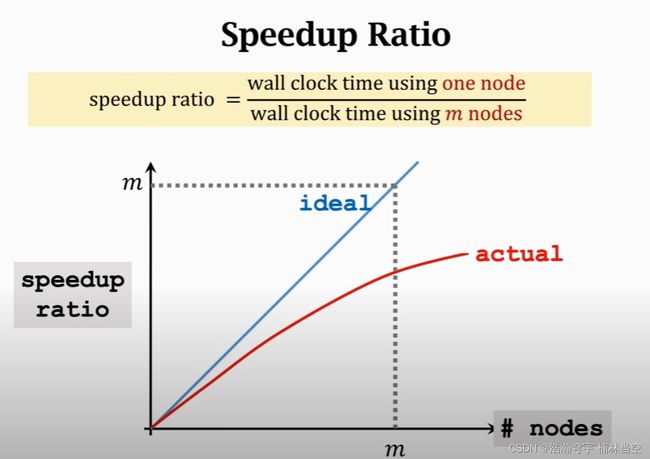
理想情况下, m m m个节点会使得计算速度增加 m m m倍(Clock Time下降至 1 m \frac{1}{m} m1),但是实际系统中有通信不同步等问题造成的时延。
可以看出,由于各个节点工作节奏不同,实际的加速比低于 m m m。因此有必要对网络中的通信代价进行分析。
网络通信代价的来源
网络中通信代价主要来自于通信复杂度(Communication Complexity)、延迟(Latency)、以及同步时延。
通信复杂度(Communication Complexity)
定义
节点之间需要传的码字个数
影响
正比于系统参数(parameters)的数量以及节点的个数
延迟(Latency)
一次发送动作的耗时,与发送次数以及网络本身有关(以发送次数为单位)
总结
有如下不准确公式: C o m m u n i c a t i o n T i m e = C o m p l e x i t y B a n d w i d t h + L a t e n c y (3) Communication Time=\frac{Complexity}{Bandwidth}+Latency \tag{3} CommunicationTime=BandwidthComplexity+Latency(3)
同步时延
对于同步系统,系统会等待所有节点完成计算工作之后再进入下一个工作循环,因此系统一次工作的时间由最慢的节点(Straggler)决定,如下图所示:
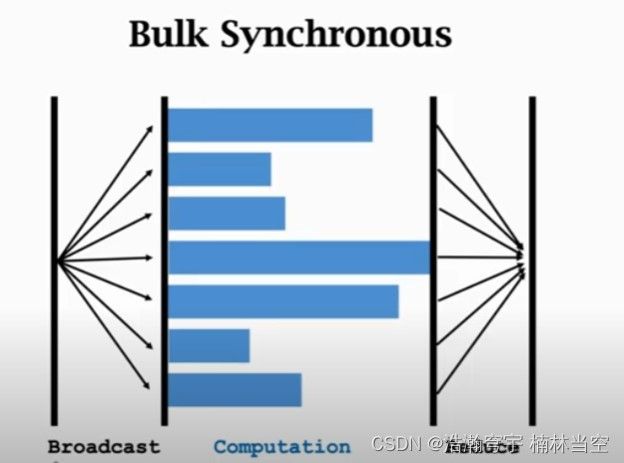
由此可知,节点数越多,Straggler的影响越大。