无线信道的信道容量
无线信道的信道容量
- 总论
-
- 来源:
- 讨论思路
- 信道容量定义及物理意义
-
- 定义
- 物理意义(David 无线通信基础)
- AWGN信道下信道容量
-
- AWGN信道(离散时间)
- 信道容量:
- 平坦衰落信道的容量
-
- CDI 已知
- CSIR
-
- 各态历经容量
-
- 内容
- 与AWGN容量的关系
- 使用场景
- 中断容量
-
- 内容
- 适用场景
- CSIRT
-
- 系统模型
- 功率控制
-
- 最优功率控制(注水法)
-
- 求解
- 物理意义
- 次优功率控制(信道反转)
- 各容量对比
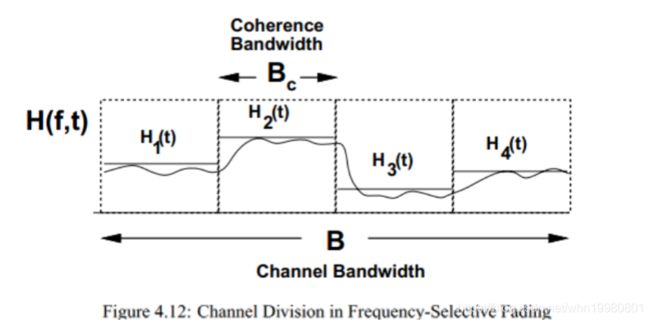
- 频率选择性信道
-
- 时不变
- 时变
总论
来源:
- Andrea Goldsmith-Wireless Communication
- David Tse-Fundamentals of Wireless Communication
讨论思路
首先从定义和物理意义角度讨论无线信道的容量是什么,此处内容主要来自于 David Tse-Fundamentals of Wireless Communication。
之后讨论在不同信道以及不同通信场景下,信道容量的值,主要有两个维度:
- 不同信道(AWGN信道、平稳时变信道、频率选择性时不变以及时变信道)
- 不同通信场景(收端知信道分布信息CDI、收端知信道信息CSIR、收发都知CSIRT)
信道容量定义及物理意义
定义
1、当误码率接近无限小时,通信系统所允许的最高传输速率。
C = m a x ( R b ∣ B E R → 0 ) C=max(R_{\mathrm{b}}|BER \rightarrow 0) C=max(Rb∣BER→0)
2、信道输入与输出的互信息量的最大值。
C = max I ( input;output ) C=\text{max }I(\text{input;output}) C=max I(input;output)
物理意义(David 无线通信基础)
根据采样定理,任何一个带宽为 B B B,时长为 T T T的信号,至少需要 N = 2 B T N=2BT N=2BT个样本才能重建,所以信号空间为 N N N维,所以任意一个信号可以看成是 N N N维欧氏空间中的一个点。
假设给定发送信号功率约束 P P P,高斯白噪声的方差为 σ 2 \sigma^{2} σ2,根据大数定律, N N N维接受矢量将高概位于半径为 N P + σ 2 \sqrt{N{P+\sigma^2}} NP+σ2的超球内,而考虑噪声的影响,对于发射星座点,对应接受矢量应高概位于半径为 N σ \sqrt{N}\sigma Nσ的噪声球附近。如果要无误通信,相邻噪声球不应该重叠,所以物理意义是将多个噪声球填充进入 N N N维信号空间的超球中,最大填充个数则是我们的信道容量:
N ( P + σ 2 ) N N σ 2 N \frac{\sqrt{N\left(P+\sigma^{2}\right)}^{N}}{\sqrt{N \sigma^{2}} N} Nσ2NN(P+σ2)N
比特化后有:
1 T log ( N ( P + σ 2 ) N N σ 2 N ) = B log ( 1 + P σ 2 ) \frac{1}{T} \log \left(\frac{\sqrt{N\left(P+\sigma^{2}\right)}^{N}}{\sqrt{N \sigma^{2}} N}\right)=B \log \left(1+\frac{P}{\sigma^{2}}\right) T1log(Nσ2NN(P+σ2)N)=Blog(1+σ2P)
物理意义图示如下:

此处推荐知乎回答
AWGN信道下信道容量
AWGN信道(离散时间)
y [ i ] = x [ i ] + n [ i ] y[i]=x[i]+n[i] y[i]=x[i]+n[i]
AWGN信道无衰落,所以接受信噪比是恒定值 γ = P / ( N 0 B ) \gamma=P /\left(N_{0} B\right) γ=P/(N0B)
信道容量:
C = B log 2 ( 1 + γ ) C=B \log _{2}(1+\gamma) C=Blog2(1+γ)
容量最大输入是高斯分布。
香农容量是数据率的上界。
平坦衰落信道的容量
在AWGN基础上加入了平坦衰落,时变的信道增益系数为 g [ i ] , 0 ≤ g [ i ] \sqrt{g[i]}, 0 \leq g[i] g[i],0≤g[i],系统模型为:
y [ i ] = g [ i ] x [ i ] + n [ i ] y[i]=\sqrt{g[i]} x[i]+n[i] y[i]=g[i]x[i]+n[i]
系统框图:

信道功率增益系数 g [ i ] g[i] g[i]服从分布 p ( g ) p(g) p(g),则接受信噪比为:
γ [ i ] = P ˉ g [ i ] / ( N 0 B ) , 0 ≤ γ [ i ] < ∞ \gamma[i]=\bar{P} g[i] /\left(N_{0} B\right), 0 \leq \gamma[i]<\infty γ[i]=Pˉg[i]/(N0B),0≤γ[i]<∞
其中 P ˉ \bar{P} Pˉ为平均发送功率。
对于信道增益的先验信息有三种:
- 信道分布信息(CDI)已知——收发都已知 g [ i ] g[i] g[i]的分布;
- 接收端已知(CSIR)——接收端已知 g [ i ] g[i] g[i]在时刻 i i i的值,且收发都已知 g [ i ] g[i] g[i]的分布;
- 发送端和接收端都已知(CSITR)。
CDI 已知
容量求解,用下式:
C = max p ( x ) I ( X ; Y ) = max p ( x ) ∑ x , y p ( x , y ) log ( p ( x , y ) p ( x ) p ( y ) ) C=\max _{p(x)} I(X ; Y)=\max _{p(x)} \sum_{x, y} p(x, y) \log \left(\frac{p(x, y)}{p(x) p(y)}\right) C=p(x)maxI(X;Y)=p(x)maxx,y∑p(x,y)log(p(x)p(y)p(x,y))
求解困难
CSIR
此时有两种讨论容量的角度:
- 各态历经容量:平均误码率为零的最大传输速率。
- 中断容量:在某个中断概率下的信道最大传输速率。
各态历经容量
内容
C = ∫ 0 ∞ B log 2 ( 1 + γ ) p ( γ ) d γ C=\int_{0}^{\infty} B \log _{2}(1+\gamma) p(\gamma) d \gamma C=∫0∞Blog2(1+γ)p(γ)dγ
这是一个理论恒定值,即不可将其理解为,当接受信噪比为 γ \gamma γ时,速率为 B log 2 ( 1 + γ ) B \log _{2}(1+\gamma) Blog2(1+γ),因为发端没有CSI,只能以恒定速率传输
与AWGN容量的关系
E [ B log 2 ( 1 + γ ) ] = ∫ B log 2 ( 1 + γ ) p ( γ ) d γ ≤ B log 2 ( 1 + E [ γ ] ) = B log 2 ( 1 + γ ˉ ) \begin{aligned} &\begin{aligned} E\left[B \log _{2}(1+\gamma)\right] &=\int B \log _{2}(1+\gamma) p(\gamma) d \gamma \\ & \leq B \log _{2}(1+E[\gamma])\\ &=B \log _{2}(1+\bar{\gamma}) \end{aligned}\\ \end{aligned} E[Blog2(1+γ)]=∫Blog2(1+γ)p(γ)dγ≤Blog2(1+E[γ])=Blog2(1+γˉ)
可见对于相同的平均接受信噪比 γ ˉ \bar{\gamma} γˉ,CSIR的信道容量小于AWGN的信道容量,这说明信道衰落总是会降低容量。
使用场景
快变信道,因为其要求信道编码应该遍历各个信道状态,而慢变信道造成的编码长度太长。
中断容量
在允许一定误码时(出错重传)的信道容量,则与各态历经相比则可以获得更高的信道容量。
内容
由可接受中断概率 p o u t p_{out} pout给一个最小的接受信噪比 p out = p ( γ < γ min ) p_{\text {out }}=p\left(\gamma<\gamma_{\min }\right) pout =p(γ<γmin),则中断容量为:
C = B log 2 ( 1 + γ min ) C=B \log _{2}\left(1+\gamma_{\min }\right) C=Blog2(1+γmin)
平均正确接收的信息率为:
C o = ( 1 − p out ) B log 2 ( 1 + γ min ) C_{o}=\left(1-p_{\text {out }}\right) B \log _{2}\left(1+\gamma_{\min }\right) Co=(1−pout )Blog2(1+γmin)
适用场景
慢变信道
CSIRT
系统模型

CSIT引入最大的不同在于,发端可以控制信息传输速率以及功率控制,进而提供容量增益。
此时信道容量为:
C = ∫ 0 ∞ C γ p ( γ ) d γ = ∫ 0 ∞ B log 2 ( 1 + γ ) p ( γ ) d γ C=\int_{0}^{\infty} C_{\gamma} p(\gamma) d \gamma=\int_{0}^{\infty} B \log _{2}(1+\gamma) p(\gamma) d \gamma C=∫0∞Cγp(γ)dγ=∫0∞Blog2(1+γ)p(γ)dγ
从上式可以看出,当CSIRT时,如果不进行功率控制,仅根据接收信噪比调整发送速率,不会增加信道容量,但可以有效提高系统的平均传输速率(使其接近CSIR信道容量)
功率控制
进行功率分配的过程数学化为:
C = max P ( γ ) : ∫ P ( γ ) p ( γ ) d γ = P ˉ ∫ 0 ∞ B log 2 ( 1 + P ( γ ) γ P ˉ ) p ( γ ) d γ C=\max _{P(\gamma): \int P(\gamma) p(\gamma) d \gamma=\bar{P}} \int_{0}^{\infty} B \log _{2}\left(1+\frac{P(\gamma) \gamma}{\bar{P}}\right) p(\gamma) d \gamma C=P(γ):∫P(γ)p(γ)dγ=Pˉmax∫0∞Blog2(1+PˉP(γ)γ)p(γ)dγ
最优功率控制(注水法)
求解
对上式,构造Lagrange:
J ( P ( γ ) ) = ∫ 0 ∞ B log 2 ( 1 + γ P ( γ ) P ˉ ) p ( γ ) d γ − λ ∫ 0 ∞ P ( γ ) p ( γ ) d γ J(P(\gamma))=\int_{0}^{\infty} B \log _{2}\left(1+\frac{\gamma P(\gamma)}{\bar{P}}\right) p(\gamma) d \gamma-\lambda \int_{0}^{\infty} P(\gamma) p(\gamma) d \gamma J(P(γ))=∫0∞Blog2(1+PˉγP(γ))p(γ)dγ−λ∫0∞P(γ)p(γ)dγ
令导数为零求极值:
∂ J ( P ( γ ) ) ∂ P ( γ ) = [ ( B / ln ( 2 ) 1 + γ P ( γ ) / P ˉ ) γ P ˉ − λ ] p ( γ ) = 0 \frac{\partial J(P(\gamma))}{\partial P(\gamma)}=\left[\left(\frac{B / \ln (2)}{1+\gamma P(\gamma) / \bar{P}}\right) \frac{\gamma}{\bar{P}}-\lambda\right] p(\gamma)=0 ∂P(γ)∂J(P(γ))=[(1+γP(γ)/PˉB/ln(2))Pˉγ−λ]p(γ)=0
解得最优功控:
P ( γ ) P ˉ = { 1 γ 0 − 1 γ γ ≥ γ 0 0 γ < γ 0 \frac{P(\gamma)}{\bar{P}}=\left\{\begin{array}{ll} \frac{1}{\gamma_{0}}-\frac{1}{\gamma} & \gamma \geq \gamma_{0} \\ 0 & \gamma<\gamma_{0} \end{array}\right. PˉP(γ)={γ01−γ10γ≥γ0γ<γ0
其中 γ 0 \gamma_{0} γ0为中断门限,表明我们仅在 γ 0 ≤ γ [ i ] < ∞ \gamma_{0} \leq \gamma[i]<\infty γ0≤γ[i]<∞使用信道。且满足:
∫ γ 0 ∞ ( 1 γ 0 − 1 γ ) p ( γ ) d γ = 1 \int_{\gamma_{0}}^{\infty}\left(\frac{1}{\gamma_{0}}-\frac{1}{\gamma}\right) p(\gamma) d \gamma=1 ∫γ0∞(γ01−γ1)p(γ)dγ=1
γ 0 \gamma_{0} γ0无闭式解,通过数值解法求解。
将上式代入原信道容量公式,有:
C = ∫ γ 0 ∞ B log 2 ( γ γ 0 ) p ( γ ) d γ C=\int_{\gamma_{0}}^{\infty} B \log _{2}\left(\frac{\gamma}{\gamma_{0}}\right) p(\gamma) d \gamma C=∫γ0∞Blog2(γ0γ)p(γ)dγ
物理意义
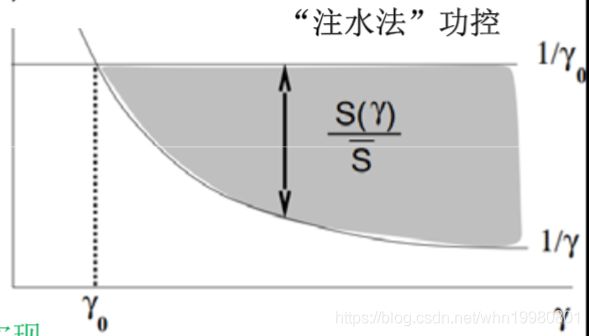
1 / γ 0 1/\gamma_{0} 1/γ0为水深, 1 / γ 1/\gamma 1/γ为碗深,我们向碗中注水直至水的总体积为总功率。
表明,在数据传输过程中,我们在信道条件好的时候( γ \gamma γ较大时),多分配功率,且用高速率传输;在信道条件差的时候( γ \gamma γ较小时),少分配功率,且用低速率传输;如果信道条件太差(低于 γ 0 \gamma_{0} γ0),则不进行数据传输。
次优功率控制(信道反转)
恒速率传输,用功控直接抵消信道衰减的影响,使得整个信道等效于AWGN信道。
信道反转由 P ( γ ) / P ˉ = σ / γ P(\gamma) / \bar{P}=\sigma / \gamma P(γ)/Pˉ=σ/γ确定, σ \sigma σ是满足功率约束条件下的恒定接收信噪比。
零中断信道容量为:
C = B log 2 [ 1 + σ ] = B log 2 [ 1 + 1 E [ 1 / γ ] ] C=B \log _{2}[1+\sigma]=B \log _{2}\left[1+\frac{1}{\mathbf{E}[1 / \gamma]}\right] C=Blog2[1+σ]=Blog2[1+E[1/γ]1]
上述也是零中断信道反转容量,当考虑中断概率时,只有条件好于中断门限才补偿,否则不传:
P ( γ ) P ˉ = { σ γ γ ≥ γ 0 0 γ < γ 0 \frac{P(\gamma)}{\bar{P}}=\left\{\begin{array}{ll} \frac{\sigma}{\gamma} & \gamma \geq \gamma_{0} \\ 0 & \gamma<\gamma_{0} \end{array}\right. PˉP(γ)={γσ0γ≥γ0γ<γ0
则中断概率为 p o u t p_{out} pout时吞吐量为:
C ( p out ) = B log 2 ( 1 + 1 E γ 0 [ 1 / γ ] ) p ( γ ≥ γ 0 ) C\left(p_{\text {out }}\right)=B \log _{2}\left(1+\frac{1}{\mathbf{E}_{\gamma_{0}}[1 / \gamma]}\right) p\left(\gamma \geq \gamma_{0}\right) C(pout )=Blog2(1+Eγ0[1/γ]1)p(γ≥γ0)
取中断概率使得上式最大即为最大中断容量:
C = max γ 0 B log 2 ( 1 + 1 E γ 0 [ 1 / γ ] ) p ( γ ≥ γ 0 ) C=\max _{\gamma_{0}} B \log _{2}\left(1+\frac{1}{\mathbf{E}_{\gamma_{0}}[1 / \gamma]}\right) p\left(\gamma \geq \gamma_{0}\right) C=γ0maxBlog2(1+Eγ0[1/γ]1)p(γ≥γ0)
其中 E γ 0 [ 1 / γ ] ≜ ∫ γ 0 ∞ 1 γ p ( γ ) d γ \mathbf{E}_{\gamma_{0}}[1 / \gamma] \triangleq \int_{\gamma_{0}}^{\infty} \frac{1}{\gamma} p(\gamma) d \gamma Eγ0[1/γ]≜∫γ0∞γ1p(γ)dγ
各容量对比
下面有对数正态分布,瑞利衰落、Nakagami衰落下容量对比,三种信道衰落剧烈程度递减:



如图关注三个问题:
- 随着信道衰减变得不剧烈(图1->图3),可以看到各个容量逐渐靠近与AWGN信道,且AWGN为任何情况最大容量。
- 瑞利衰落及Nakagami衰落可以看出,低信噪比下CSIRT接近AWGN甚至大于AWGN,这是由于AWGN是高信噪比下的恒速率传输,当平均信噪比低时,其容量较低,而CSIRT由于是注水法功控,放弃了低信噪比信道而集中功率及速率与偶尔出现的高信噪比信道实现,则会出现容量高于AWGN的情况。
- CSIRT相比CSIR,比较靠近且增益不大,这说明信道容量增益主要贡献者是发端的速率控制,功率控制的贡献度不大。
频率选择性信道
基本等同于平台衰落,仅是问题构建不同,这里只讨论CSIRT
时不变
按频率切开:
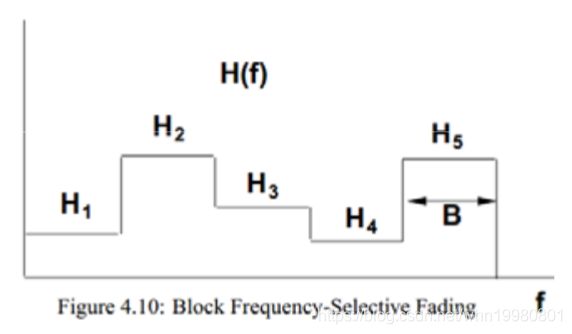
容量:
C = ∑ max P j : ∑ j P j ≤ P B log 2 ( 1 + ∣ H j ∣ 2 P j N 0 B ) C=\sum_{\max P_{j}: \sum_{j} P_{j} \leq P} B \log _{2}\left(1+\frac{\left|H_{j}\right|^{2} P_{j}}{N_{0} B}\right) C=maxPj:∑jPj≤P∑Blog2(1+N0B∣Hj∣2Pj)
功控采用频率注水:
P j P = { 1 γ 0 − 1 γ j γ j ≥ γ 0 0 γ j < γ 0 \frac{P_{j}}{P}=\left\{\begin{array}{ll} \frac{1}{\gamma_{0}}-\frac{1}{\gamma_{j}} & \gamma_{j} \geq \gamma_{0} \\ 0 & \gamma_{j}<\gamma_{0} \end{array}\right. PPj={γ01−γj10γj≥γ0γj<γ0