torch.nn里的损失函数:MSE、BCE、BCEWithLogits、NLLLoss、CrossEntropyLoss的用法
1. nn.MSELoss()
模型的预测值与标签的L2距离。一般用于回归问题。之所以不用于分类问题,可能原因为:使用sigmoid之后,函数形式不是凸函数 ,不容易求解 ,容易进入局部最优。
loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss(input, target)
output.backward()
2. nn.BCELoss()
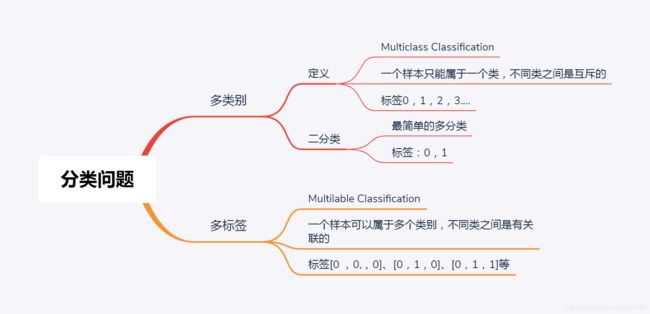
交叉熵损失函数,衡量两个分布之间的差异,一般用于分类问题。输入的x值需先经过sigmoid压缩到(0,1)之间。标签形式为[0, 0, 1], [0, 1, 1]等,各个类别预测概率独立,类与类之间不互斥,可见不仅能用于二分类问题,也能用于多标签分类问题。
m = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(m(input), target)
output.backward()
3. nn.BCEWithLogitsLoss()
交叉熵损失函数, 与nn.BCELoss()不同的是网络的输出无需用sigmoid压缩,函数内部整合了nn.sigmoid()和nn.BCELoss(),并且使用log-sum-exp trick提高了数值稳定性。同样可用于二分类及多标签分类。
这里简单介绍一下log-sum-exp trick:
原始的log-sum-exp公式为:
y = l o g ∑ i e x i y = log\sum_{i}^{}e^{x_{i}} y=logi∑exi
在 x i x_{i} xi都很小时, ∑ i e x i \sum_{i}^{}e^{x_{i}} ∑iexi趋近于0,导致数值计算问题。
而如果 x i x_{i} xi很大, ∑ i e x i \sum_{i}^{}e^{x_{i}} ∑iexi也会很大,同样会导致数值计算问题。
而log-sum-exp trick的计算公式为:
a = m a x ( x i ) a = max(x_{i}) a=max(xi)
y = a + l o g ∑ i e x i − a y = a + log\sum_{i}^{}e^{x_{i}-a} y=a+logi∑exi−a
其中 e x i − a ≤ 1 e^{x_{i}-a}\leq 1 exi−a≤1,使 ∑ i e x i \sum_{i}^{}e^{x_{i}} ∑iexi既不会趋于0也不会很大,避免数值溢出。
loss = nn.BCEWithLogitsLoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)
output = loss(input, target)
output.backward()
4. nn.LogSoftmax()
将输入softmax后取对数
m = nn.LogSoftmax()
input = torch.randn(2, 3)
output = m(input)
5. nn.NLLLoss()
NLLLoss需要配合nn.LogSoftmax()使用,网络输出的值经过nn.LogSoftmax()后传入NLLLoss()。其标签实际上就是网络输出里对应数值的索引,通过这个索引取得对应的值并去掉负号。如果是一批次的话,还需要求均值。由于网络输出需先经过softmax,各个类别预测概率之和为1,所以类与类之间互斥,用于多类别问题。
loss = nn.NLLLoss()
m = nn.LogSoftmax(dim=1)
loss = nn.NLLLoss()
# input is of size N x C = 3 x 5
input = torch.randn(3, 5, requires_grad=True)
# each element in target has to have 0 <= value < C
target = torch.tensor([1, 0, 4])
output = loss(m(input), target)
output.backward()
# 2D loss example (used, for example, with image inputs)
N, C = 5, 4
loss = nn.NLLLoss()
# input is of size N x C x height x width
data = torch.randn(N, 16, 10, 10)
conv = nn.Conv2d(16, C, (3, 3))
m = nn.LogSoftmax(dim=1)
# each element in target has to have 0 <= value < C
target = torch.empty(N, 8, 8, dtype=torch.long).random_(0, C)
output = loss(m(conv(data)), target)
output.backward()
6. nn.CrossEntropyLoss()
nn.CrossEntropyLoss()是nn.logSoftmax()和nn.NLLLoss()的整合,适用于多类别问题。
loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)
output = loss(input, target)
output.backward()