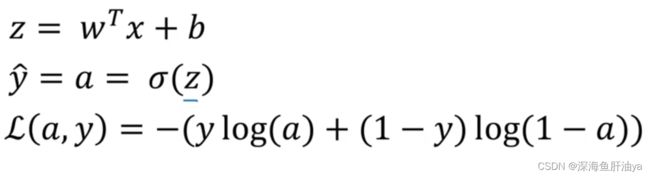向毕业妥协系列之深度学习笔记(一)浅层神经网络
目录
一.神经网络杂记
二.计算图(反向传播求导的几个实例)
1.普通式子反向传播求导
2.逻辑回归中的梯度下降
3.m个样本的梯度下降
三.向量化
四.python广播
五.激活函数
六.随机初始化
深度学习系列的文章也可以结合下面的笔记来看:
深度学习笔记-目录
一.神经网络杂记
这个系列的学习和机器学习系列的课程有很多重复的部分,尤其是神经网络的一些基础知识,以及什么回归等知识,所以很多东西如果我机器学习的文章当中有的话,我就略过了或者简单提一嘴。(可能有很多不同的内容,但是大部分已经在机器学习学过了,故而将本节取名为杂记)
可以看一下我的机器学习系列的入门文章(开头前缀是:“向毕业妥协系列之机器学习笔记”):
https://blog.csdn.net/weixin_44593822/category_12091831.html?spm=1001.2014.3001.5482
卷积神经网络我们还会学习很多不同类型的神经网络,比如CNN(适用于图像数据),RNN(循环神经网络,非常适合处理一维序列数据)
结构化数据和非结构化数据的直观理解:
为什么神经网络会兴起?看到下面的机器学习和神经网络的随着数据量的提升,他们性能上的变化就可以知道深度学习更加适合现在这个大数据时代。
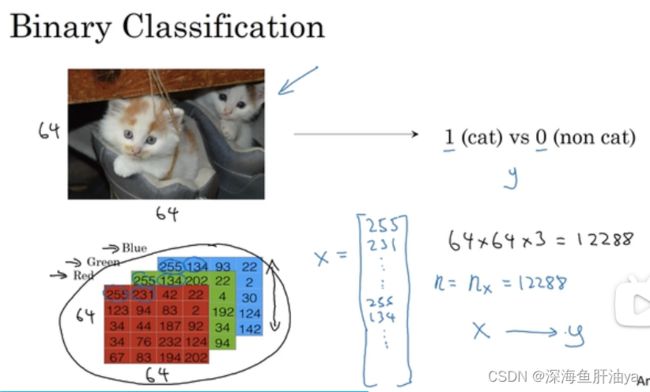
下面是一个二元分类,简单提一嘴吧,想起了大三的时候学的CNN,当时也是这个例子,一张图片的每一个像素有红绿蓝三原色组成,即三个矩阵,三个矩阵的叠加,然后图片作为一个输入数据,展开成一个张量,比如一个64*64的图片,它的特征有64*64*3个特征。
符号定义 :
逻辑回归:
蓝色部分的符号是本门课用的符号,红色部分的符号可能在其他的资料中用这个,但是Andrew还是那句话:Don't worry about it
损失函数和成本函数:
损失函数定义的是单个训练样本的预测与真实值的差值损失,而成本函数是对于总体样本的的预测与真实值的差值损失
梯度下降:
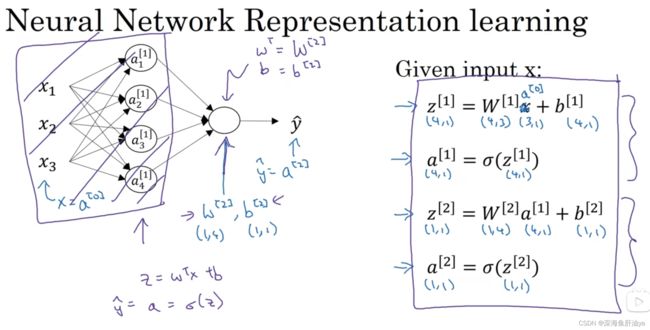
计算神经网络输出:
向量化:
二.计算图(反向传播求导的几个实例)
1.普通式子反向传播求导
可以说,一个神经网络的计算,都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。计算图解释了为什么我们用这种方式组织这些计算过程。
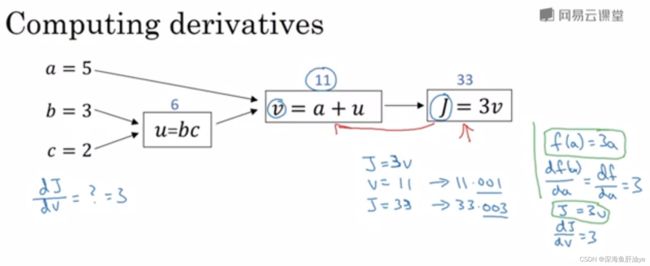
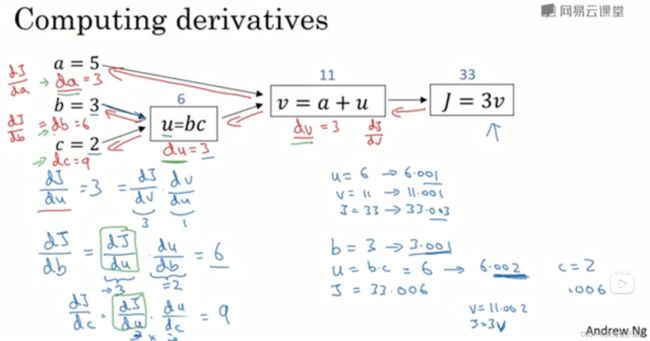
下图是一个式子的计算过程,我们的思维是从左到右一步一步最后得到结果,但是我们接下来讲解的如何求偏导,求解偏导的过程与这个方向是相反的,即从右到左。
反向传播求导过程:
先回忆一下高数中对于导数的理解,当然我快一年没学了,记不太清了,但是你要求J关于v的导数,是不是得看看J的增量和v的增量的关系,咱们看到下式J=3v,所以v从11变成11.001时,J变成了33.003,所J的增量是0.003,v的增量是0.001,所以导数是dJ/dv=0.003/0.001=3,这就完成了第一步反向传播。
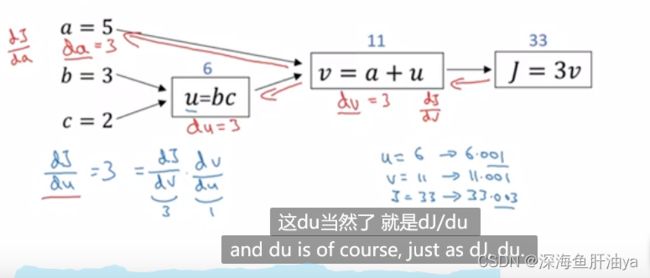
然后我们再来看看a的变化对于J有什么影响,即求dJ/da
上图可以看到我们让a从5变到5.001,那么v就会从11变到11.001,继而J就会从33变到33.003,所以继续用J的变化量去除a的变化量,得到dJ/da=3,用v的变化量去除a的变化量就能得到
dv/da=1,然后咱们根据公式可以看到,a的变化可以引起v的变化,v的变化可以引起J的变化,所以当求J对a的导时,可以应用链式法则,即dJ/da=(dJ/dv)*(dv/da)=3*1=3,所以反向传播求dJ/da就是第一步反向传播是求dJ/dv=3,第二步求dv/da=1,然后第二跳到a的时候把这两步的导数乘起来得到咱们想求的导数即可。
另外咱们写代码的时候通常把自己最终要求得的那个导数(dJ/da)记为dvar,dJ/dv记为dv,dJ/da记为da。
用上面的方法来计算一下dJ/du(代码里记作du),有了上面的经验,下图可以看懂
同样的道理我们也可以计算出dJ/db和dJ/dc
2.逻辑回归中的梯度下降
a是yhat
3.m个样本的梯度下降
通过上节的推导咱们已经可以知道如何求对于单个训练样本损失函数的导,现在我们来看看对于成本函数求导。假设我们的例子中只有两个特征,如下用for循环对个示例依次遍历,最终得到dJ/dw_1,dJ/dw_2,dJ/db
神经网络就是 正向算一遍loss,然后反向传播一遍偏导。
至于神经网络里的反向传播我就不手撕,我自己也先跳过了,毕竟抓紧学学搞工程,暂且用不到的理论先放放也行。
三.向量化
也是机器学习中学过的概念,即尽量避免for循环,用矩阵运算什么的(numpy)。
可以看我机器学习的系列文章,也可以参考本篇文章开头给的深度学习笔记链接。
四.python广播
一些通用原则:
当你用(m,n)的矩阵去对(1,n)的矩阵做加减乘除操作时,python的广播机制会把(1,n)的矩阵变成(m,n)的矩阵。下图其他的也可以看懂,自己看看吧。
吴老师的建议:
在写代码时不要用那种秩1数组,就是那种打印数组shape输出个诸如(5,)之类的数组,这既不是行向量也不是列向量,吴老师建议我们使用尺寸明确的矩阵(看下图),也可以用reshape重塑一下矩阵尺寸,比如即便心里知道这是个(1,5)的矩阵也可以调用一下reshape(1,5),确保无误.
五.激活函数
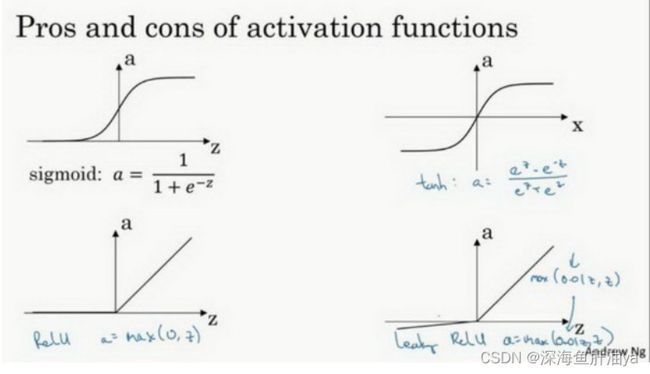
更通常的情况下,激活函数可以是除了sigmoid函数以外的非线性函数。tanh函数或者双曲正切函数是总体上都优于sigmoid函数的激活函数。
a=tan(z)的值域是位于+1和-1之间。
sigmoid函数和tanh函数两者共同的缺点是,在特别大或者特别小的情况下,导数的梯度或者函数的斜率会变得特别小,最后就会接近于0,导致降低梯度下降的速度。因为导数小了,所以每次下降的距离就小了,尤其是斜率接近于0的时候,回想一下,梯度下降的公式就知道了。
这有一些选择激活函数的经验法则:
如果输出是0、1值(二分类问题),则输出层选择sigmoid函数,然后其它的所有单元都选择Relu函数。
这是很多激活函数的默认选择,如果在隐藏层上不确定使用哪个激活函数,那么通常会使用Relu激活函数。有时,也会使用tanh激活函数,但Relu的一个优点是:当z是负值的时候,导数等于0。
这里也有另一个版本的Relu被称为Leaky Relu。
当z是负值时,这个函数的值不是等于0,而是轻微的倾斜,如图。
这个函数通常比Relu激活函数效果要好,尽管在实际中Leaky ReLu使用的并不多。
两者的优点是:
第一,在z的区间变动很大的情况下,激活函数的导数或者激活函数的斜率都会远大于0,在程序实现就是一个if-else语句,而sigmoid函数需要进行浮点四则运算,在实践中,使用ReLu激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。
第二,sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于0,这会造成梯度弥散,而Relu和Leaky ReLu函数大于0部分都为常数,不会产生梯度弥散现象。(同时应该注意到的是,Relu进入负半区的时候,梯度为0,神经元此时不会训练,产生所谓的稀疏性,而Leaky ReLu不会有这问题)
z在ReLu的梯度一半都是0,但是,有足够的隐藏层使得z值大于0,所以对大多数的训练数据来说学习过程仍然可以很快。
快速概括一下不同激活函数的过程和结论。
sigmoid激活函数:除了输出层是一个二分类问题基本不会用它。
tanh激活函数:tanh是非常优秀的,几乎适合所有场合。
ReLu激活函数:最常用的默认函数,,如果不确定用哪个激活函数,就使用ReLu或者Leaky ReLu。a=max(0.01z,z)为什么常数是0.01?当然,可以为学习算法选择不同的参数。
在选择自己神经网络的激活函数时,有一定的直观感受,在深度学习中的经常遇到一个问题:在编写神经网络的时候,会有很多选择:隐藏层单元的个数、激活函数的选择、初始化权值……这些选择想得到一个对比较好的指导原则是挺困难的。
鉴于以上三个原因,以及在工业界的见闻,提供一种直观的感受,哪一种工业界用的多,哪一种用的少。但是,自己的神经网络的应用,以及其特殊性,是很难提前知道选择哪些效果更好。所以通常的建议是:如果不确定哪一个激活函数效果更好,可以把它们都试试,然后在验证集或者发展集上进行评价。然后看哪一种表现的更好,就去使用它。
为自己的神经网络的应用测试这些不同的选择,会在以后检验自己的神经网络或者评估算法的时候,看到不同的效果。如果仅仅遵守使用默认的ReLu激活函数,而不要用其他的激励函数,那就可能在近期或者往后,每次解决问题的时候都使用相同的办法。
至于为什么要用激活函数?
不引入非线性的激活函数的话,最后输出还是个线性的,不能做很多有趣的计算。
非线性是指两个变量间的数学关系,不是直线,而是曲线、曲面、或不确定的属性,是不成简单比例(即线性)关系的。
推导证明去看我机器学习系列的文章吧。
六.随机初始化
初始化时要随机初始化,而不要将参数全部设为0,对于参数b来说可以设置全0,因为这样不会造成参数矩阵的完全对称化,,但是对于参数w来说,不可以设置为全0,如果全0,会让参数矩阵完全对称化。所以权重通常是随机生成,并且再乘上一个非常小的数(防止当使用sigmoid函数或tanh函数时,z过大或或过小造成进入到激活函数的平坦部分致使梯度下降缓慢)。详情直接看深度学习笔记链接。