从Q-Learning到Deep-Q-Learning

Deep Learning

定义

深度学习(Deep Learing)由一组算法和技术构成，这些算法和技术试图发现数据的重要特征并对其高级抽象建模。深度学习的主要目标是通过对数据的自动学习来避免手动描述数据结构(如手写特征)。深度指的是通常具有两个或多个隐藏层的任何神经网络即(DNN)。

大多数深度学习模型都基于人工神经网络（ANN），尽管它们也可以包含命题公式或在深度生成模型中分层组织的潜在变量，例如Deep Belief Networks和Deep Boltzmann Machines中的节点。

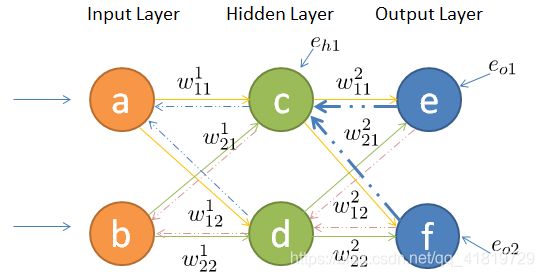
人工神经网络是一种基于大脑神经结构的计算非线性模型，能够学习执行诸如分类，预测，决策和可视化之类的任务。一个人工神经网络由人工神经元组成，并组织为三个相互关联的层：输入，隐藏和输出，如图中的（b）所示。

a）强化学习，（b）人工神经网络和（c）深度Q学习

输入层包含将信息发送到隐藏层的输入神经元。隐藏层将数据发送到输出层。每个神经元都有加权的输入（突触），一个激活函数和一个输出。突触是可调整的参数，可将神经网络转换为参数化系统。节点的激活函数定义给定输入的该节点的输出。特别是，激活函数将根据所选的激活功能将输入值映射到目标范围。例如，logistic activation function会将实数域中的所有输入映射到0到1的范围内。

在训练阶段，人工神经网络使用反向传播作为有效的学习算法来快速计算权重的梯度下降。反向传播是自动微分的一种特殊情况。在学习的上下文(context)中，反向传播是梯度下降优化算法中常用的通过计算损失函数的梯度来调整神经元权值的方法。这种技术有时也称为误差(errors/loss)后向传播，因为损失(loss)是在输出端计算出来的，并通过网络层反向传播回来。

具体算法细节

典型DNN模型

DNN被定义为具有多个隐藏层的ANN。有两种典型的DNN模型，即前馈神经网络（FNN）和递归神经网络（RNN）。

Fig. 1.FNN and RNN

FNN

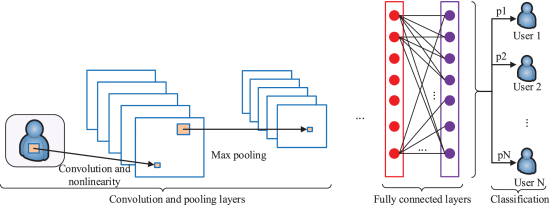
在FNN中，信息仅在一个方向上移动，即从输入节点经过隐藏节点再到输出节点，并且网络中没有循环或循环，如图1所示。在FNN中，卷积神经网络（CNN）是最著名的模型，具有广泛的应用，尤其是在图像和语音识别中。CNN包含一个或多个集合或完全连接的卷积层，并使用了上面讨论的多层感知器的变体。通常，CNN具有两个主要组件，即特征提取和分类，如图2所示。特征提取组件被放置在隐藏层，目的是执行一系列卷积和池操作，并且在此期间检测特征。然后，分类组件放置在全连接层，将为我们需要预测的对象（例如图像）分配一个概率。

Fig. 2. An illustration of CNN.

RNN

与FNN不同，RNN是递归人工神经网络的一种变体，其中神经元之间的连接构成有向循环。这意味着输出不仅取决于其直接输入，还取决于上一步的神经元状态。

循环神经网络（Recurrent Neural Network，RNN）是一种用于处理序列数据的神经网络。相比一般的神经网络来说，他能够处理序列变化的数据。比如某个单词的意思会因为上文提到的内容不同而有不同的含义，RNN就能够很好地解决这类问题。

当current step与previous step有某种关系时，通过序列形式的输入，我们能够得到如下形式的RNN。

Fig.3.RNN模型

这使得RNN非常适合具有时间成分的应用场景，例如时间序列数据和自然语言处理。但是，所有RNN在递归层中都有反馈回路。这使RNN可以随着时间的推移在内存中维护信息。

然而，训练标准RNN很难解决需要学习长期时间依赖性的问题。原因是损失函数的梯度随时间呈指数衰减，这就是所谓的消失梯度问题。因此，RNN中经常使用 长短时记忆(LSTM) 来解决此问题。

LSTM被设计为对时间序列建模，并且它们的长期依赖性比常规RNN更准确。特别的是，LSTM通过合并内存单元(Memory)提供了一种解决方案，允许网络学习何时忘记以前的隐藏状态，以及何时更新给定新信息的隐藏状态。通常，LSTM单元以具有三个或四个“门”(gate)的“块”(block)实现，例如，

• input gate(输入门)
• forget gate(忘记门)
• output gate(输出门)
• input modulation(输入调制门)

图4展示了LSTM控制逻辑功能的信息流图：

Fig. 4. An illustration of a basic (a) LSTM and (b) RNN cell.

与RNN不同，LSTM内存单元由三个组件组成

• 上个内存单元$c_t$ (the previous memory cell)
• 当前输入 $x_t$
• 上个的隐藏状态$h_{t-1}$

在这里，输入门和忘记门将用于选择性地忘记其先前的内存(memory)或考虑其当前输入。同样，输出门将学习有多少内存单位(memory cell)要转移到隐藏状态。这些额外的模块使LSTM能够学习RNN无法完成的极其复杂的长期时间动态。

LSTM结构

参考自https://zhuanlan.zhihu.com/p/32085405

首先使用LSTM的当前输入 $x^t$和上一个状态传递下来的 $h^{t-1}$ 拼接训练得到四个状态。

其中，$z^f,z^i,z^o$是由拼接向量乘以权重矩阵之后，再通过一个 $sigmoid$激活函数转换成0到1之间的数值，来作为一种门控状态。而 $z$则是将结果通过一个$tanh$激活函数转换成-1到1之间的值（这里使用$tanh$是因为这里是将其做为输入数据，而不是门控信号）。

这四个状态在LSTM内部的使用

$\odot$是Hadamard Product，也就是操作矩阵中对应的元素相乘，因此要求两个相乘矩阵是同型的。 $\oplus$则代表进行矩阵加法。

LSTM内部主要有三个阶段：

(1) 忘记阶段。这个阶段主要是对上一个节点传进来的输入进行选择性忘记。简单来说就是会 “忘记不重要的，记住重要的”。

具体来说是通过计算得到的 $z^f$ f表示forget）来作为忘记门控，来控制上一个状态的 $c^{t-1}$ 哪些需要留哪些需要忘。

(2) 选择记忆阶段。这个阶段将这个阶段的输入有选择性地进行“记忆”。主要是会对输入$x^t$ 进行选择记忆。哪些重要则着重记录下来，哪些不重要，则少记一些。当前的输入内容由前面计算得到的$z$表示。而选择的门控信号则是由 $z^i$（i代表information）来进行控制。

将上面两步得到的结果相加，即可得到传输给下一个状态的 $c^t$ 。也就是上图中的第一个公式。

(3) 输出阶段。这个阶段将决定哪些将会被当成当前状态的输出。主要是通过 $c^o$ 来进行控制的。并且还对上一阶段得到的 $c^o$ 进行了放缩（通过一个tanh激活函数进行变化）。

与普通RNN类似，输出 $y^t$ 往往最终也是通过 $h^t$ 变化得到。

总结

以上，就是LSTM的内部结构。通过门控状态来控制传输状态，记住需要长时间记忆的，忘记不重要的信息；而不像普通的RNN那样只能够“呆萌”地仅有一种记忆叠加方式。对很多需要“长期记忆”的任务来说，尤其好用。

但也因为引入了很多内容，导致参数变多，也使得训练难度加大了很多。因此很多时候我们往往会使用效果和LSTM相当但参数更少的GRU来构建大训练量的模型。

Deep Q-Learning

通过上一篇对Q-Learning的分析，我们知道Q-Learning模型的训练结果是一张存储了Q-Value的表。

Q-Value(Q值)是(s,a)状态-动作元组对的映射结果

Q值是以表格的形式给出（比如纵列为状态，横列为动作）

当状态空间和动作空间较小时也即在许多简单的问题中，这种表格型的Q-Learning方法是比较实用的，Q-Learning算法能有效地获得最优策略，但是当我们所处理的问题具有较大的状态集合动作集时，这种表格型的方法就显得十分的低效了。然而，在实际应用中，由于系统模型复杂，这些空间往往很大。因此，Q-Learning可能无法找到最优策略。

为此，引入深度Q学习（DQL）算法来克服这一缺点。直观地说，DQL算法实现了一个深度Q-网络（DQN）即DNN来代替Q-table，以获得$Q^{\ast }(s,a)$的近似值，如下图©所示

a）强化学习，（b）人工神经网络和（c）深度Q学习

Deep Q-Learning(DQN),通过在探索的过程中训练网络，最后所达到的目标就是将当前状态输入，得到的输出就是对应它的动作值函数,即$f(s)=q(s,a)$,这个$f$ 就是训练的网络

当使用非线性函数逼近器(比如$softmax$)时，通过强化学习算法获得的平均回报(reward)可能不稳定甚至发散。这是因为Q值的微小变化也可能会对策略(${\pi }^{\ast }$)产生很大影响。因此，数据分布和Q值与相关系数($Q-value$和target values:$R+\gamma {\max }_{a^{\prime }}\mathcal{Q}(s^{\prime },a^{\prime })$ )是不断变化的。为了解决这个问题，可以使用两种机制/算法(这也是DQN中的两个重要特性)：

• Experience Replay mechanism：

  • 记忆回放（experience replay mechanism) 是用来解决数据关联性问题的;

  为了让 RL 的数据 （关联性不独立分布的数据） 更接近DL所需要的数据 （独立同分布数据），在学习过程中建立一个“经验池(replay memory pool)”即$D=(s_{t}, a_{t}, r_{t}, s_{t+1}) $，将一段时间内的state($s_t$ )、action($a_t$ )、state_ (下一时刻状态$s_{t+1}$） 以及 reward ($r_t$ )存储在经验池里，每次训练神经网络时，从经验池里随机抽取一个batch的经验(experience)用于当前的训练，

  通过随机抽取的操作打乱了原始数据的顺序，将数据的关联性减弱

  经过训练的DNN获得的Q-Value又将通过转换存入经验池中 用于下一次训练中获得新的经验(experience)。

• Fixed target Q -network:

  • 为了使得算法性能更稳定，建立两个结构一样的神经网络：一直在更新神经网络参数的网络 （MainNet) 和用于更新Q值的网络（TargetNet)。

  在训练过程中，Q值会不断发生变化。因此，如果使用一组不断移动的值(values)来更新Q-network，则value estimations可能会失去控制。这会导致算法的不稳定。为了解决这个问题，目标Q网络TargetNet被用来频繁但缓慢地更新主Q网络MainNet的值。这样，目标和估计Q值之间的相关性显著降低，从而稳定了算法。工作步骤如下

  • 初始时刻将MainNet的参数赋值给TargetNet
  • 然后MainNet继续更新神经网络参数，而TargetNet的参数固定不动。
  • 再过一段时间（比如N步迭代后）将MainNet的参数赋给TargetNet，如此循环往复

  这样使得一段时间内的目标Q值是稳定不变的，从而使得算法更新更加稳定。

在MainNet中进行训练，每进行多次训练以后，将训练后的权值等参数赋给TargetNet，所以在搭建TargetNet网络时，不需要计算Loss和考虑Train过程，在MainNet中的Loss计算方法为：

$$L(\theta )=[r_j+\gamma \underset{a_{j+1}}{\max }\hat{\mathcal{Q}}(s_{j+1},a_{j+1};{\mathbf{\theta }}^{\prime })-\mathcal{Q}(s_j,a_j;\mathbf{\theta }){]}^2$$

其中$\theta$ 是神经网络的参数

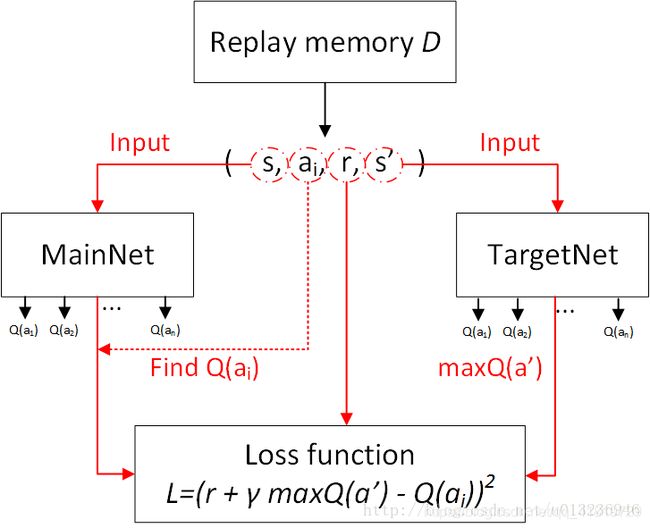
误差函数构造示意图：

如下图所示：我们在学习的过程中，会设定一个Memory空间，这个空间会记录好每一次的MDP过程，也即
$$D=(s_t,a_t,r_t,s_{t+1})$$
在一开始时，Memory pool $D$会先收集记录，当记录达到一定数量时，开始学习，每次从memory pool中随机选择一个mini-batch记忆块，这些记忆块中包含了经验（experience(s,a,s')）也即MDP过程，并且是随机选择的，所以解决了记录相关性的问题。

将这些经验中的$s_t$ (当前状态)作为输入，传入到MainNet计算出$Q(s,a,\theta )$ (当前状态的Q值)作为Q-MainNet,经过Q-Learning算法对$\theta$进行N步迭代优化为${\theta }^{\prime }$。

之后再将MainNet训练后(N步)的参数${\theta }^{\prime },a_t,s_{t+1}$ 赋给TargetNet,得到$Q(s_{t+1},a_t,{\theta }^{\prime })$ 即预测结果所映射的Q值。，赋值完成以后，通过${\max }_{a_{j+1}}\hat{\mathcal{Q}}\left(s_{t+1},a_{t+1};{\mathbf{\theta }}^{\prime }\right)$ 来计算下一步的动作$a_{t+1}$ 以及其对应的Q-TargetNet值$\hat{\mathcal{Q}}\left(s_{t+1},a_{t+1};{\mathbf{\theta }}^{\prime }\right)$，从而计算Loss，继而通过SVD优化MainNet。

算法流程图

$s^{\prime }$等价于$s_{t+1}$

$a^{\prime }$等价于$a_{t+1}$

Algorithm 2 The DQL Algorithm With Experience Replay and Fixed Target Q -Network

---

Initialize replay memory D.

Initialize the Main Q -network $\mathbf{Q}$ with random weights $\mathbf{\theta }$ .

Initialize the target Q -network $\hat{\mathbf{Q}}$ with random weights ${\mathbf{\theta }}^{\prime }$ .

for episode=1 to T do

​ With probability ϵ select a random action $a_t$ , otherwise select $a_t=\arg \max {\mathcal{Q}}^{\ast }(s_t,a_t,\mathbf{\theta })$ .

​ Perform action $a_t$ and observe immediate reward $r_t$ and next state $s_{t+1}$ .

​ Store transition $(s_t,a_t,r_t,s_{t+1})$in D.

​ Select randomly samples $\text{c}(s_j,a_j,r_j,s_{j+1})$ from D.

​ The weights of the neural network then are optimized by using stochastic gradient descent with respect to the network parameter θ to minimize the loss:

$$[r_j+\gamma \underset{a_{j+1}}{\max }\hat{\mathcal{Q}}(s_{j+1},a_{j+1};{\mathbf{\theta }}^{\prime })-\mathcal{Q}(s_j,a_j;\mathbf{\theta }){]}^2$$
​ Reset $\hat{\mathbf{Q}}=\mathbf{Q}$ after every a fixed number of steps.

end for

---

示意图：

参考：

https://blog.csdn.net/u013236946/article/details/72871858

https://ieeexplore.ieee.org/document/8714026

https://blog.csdn.net/LagrangeSK/article/details/80321265