机器学习——决策树模型:Python实现
机器学习——决策树模型:Python实现
- 1 决策树模型的代码实现
-
- 1.1 分类决策树模型(DecisionTreeClassifier)
- 1.2 回归决策树模型(DecisionTreeRegressor)
- 2 案例实战:员工离职预测模型搭建
-
- 2.1 模型搭建
- 2.2 模型预测及评估
-
- 2.2.1 直接预测是否离职
- 2.2.2 预测不离职&离职概率
- 2.2.3 模型预测及评估
- 2.2.4 特征重要性评估
- 3 参数调优 - K折交叉验证 & GridSearch网格搜索
-
- 3.1 K折交叉验证
- 3.2 GridSearch网格搜索
-
- 3.2.1 单参数调优
- 3.2.2 多参数调优
1 决策树模型的代码实现
决策树模型既可以做分类分析(即预测分类变量值),也可以做回归分析(即预测连续变量值),分别对应的模型为分类决策树模型(DecisionTreeClassifier)及回归决策树模型(DecisionTreeRegressor)。
1.1 分类决策树模型(DecisionTreeClassifier)
from sklearn.tree import DecisionTreeClassifier
X = [[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]]
y = [1, 0, 0, 1, 1]
model = DecisionTreeClassifier(random_state=0)
model.fit(X, y)
print(model.predict([[5, 5]]))
1.2 回归决策树模型(DecisionTreeRegressor)
from sklearn.tree import DecisionTreeRegressor
X = [[1, 2], [3, 4], [5, 6], [7, 8], [9, 10]]
y = [1, 2, 3, 4, 5]
model = DecisionTreeRegressor(max_depth=2, random_state=0)
model.fit(X, y)
print(model.predict([[9, 9]]))
2 案例实战:员工离职预测模型搭建
2.1 模型搭建
# 1.读取数据与简单预处理
import pandas as pd
df = pd.read_excel('员工离职预测模型.xlsx')
df = df.replace({'工资': {'低': 0, '中': 1, '高': 2}})
# 2.提取特征变量和目标变量
X = df.drop(columns='离职')
y = df['离职']
# 3.划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
# 4.模型训练及搭建
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(max_depth=3, random_state=123)
model.fit(X_train, y_train)
2.2 模型预测及评估
2.2.1 直接预测是否离职
y_pred = model.predict(X_test)
print(y_pred[0:100])
# 通过构造DataFrame进行对比
a = pd.DataFrame() # 创建一个空DataFrame
a['预测值'] = list(y_pred)
a['实际值'] = list(y_test)
a.head()
# 如果要查看整体的预测准确度,可以采用如下代码:
from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)
# 或者用模型自带的score函数查看预测准确度
model.score(X_test, y_test)
2.2.2 预测不离职&离职概率
其实分类决策树模型本质预测的并不是准确的0或1的分类,而是预测其属于某一分类的概率,可以通过如下代码查看预测属于各个分类的概率:
y_pred_proba = model.predict_proba(X_test)
print(y_pred_proba[0:5])
b = pd.DataFrame(y_pred_proba, columns=['不离职概率', '离职概率'])
b.head()
如果想查看离职概率,即查看y_pred_proba的第二列,可以采用如下代码,这个是二维数组选取列的方法,其中逗号前的“:”表示所有行,逗号后面的数字1则表示第二列,如果把数字1改成数字0,则提取第一列不离职概率。
y_pred_proba[:,1]
2.2.3 模型预测及评估
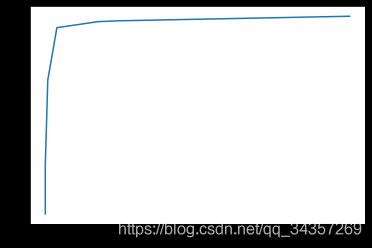
在Python实现上,可以求出在不同阈值下的命中率(TPR)以及假警报率(FPR)的值,从而可以绘制ROC曲线。
from sklearn.metrics import roc_curve
fpr, tpr, thres = roc_curve(y_test, y_pred_proba[:,1])
已知了不同阈值下的假警报率和命中率,可通过matplotlib库可绘制ROC曲线,代码如下:
import matplotlib.pyplot as plt
plt.plot(fpr, tpr)
plt.show()
from sklearn.metrics import roc_auc_score
score = roc_auc_score(y_test, y_pred_proba[:,1])
print(score)
2.2.4 特征重要性评估
model.feature_importances_
# 通过DataFrame进行展示,并根据重要性进行倒序排列
features = X.columns # 获取特征名称
importances = model.feature_importances_ # 获取特征重要性
# 通过二维表格形式显示
importances_df = pd.DataFrame()
importances_df['特征名称'] = features
importances_df['特征重要性'] = importances
importances_df.sort_values('特征重要性', ascending=False)
3 参数调优 - K折交叉验证 & GridSearch网格搜索
3.1 K折交叉验证
from sklearn.model_selection import cross_val_score
acc = cross_val_score(model, X, y, scoring='roc_auc', cv=5)
acc
acc.mean()
3.2 GridSearch网格搜索
3.2.1 单参数调优
from sklearn.model_selection import GridSearchCV # 网格搜索合适的超参数
# 指定参数k的范围
parameters = {'max_depth': [3, 5, 7, 9, 11]}
# 构建决策树分类器
model = DecisionTreeClassifier() # 这里因为要进行参数调优,所以不需要传入固定的参数了
# 网格搜索
grid_search = GridSearchCV(model, parameters, scoring='roc_auc', cv=5) # cv=5表示交叉验证5次,默认值为3;scoring='roc_auc'表示通过ROC曲线的AUC值来进行评分,默认通过准确度评分
grid_search.fit(X_train, y_train)
# 输出参数的最优值
grid_search.best_params_
3.2.2 多参数调优
from sklearn.model_selection import GridSearchCV
# 指定决策树分类器中各个参数的范围
parameters = {'max_depth': [5, 7, 9, 11, 13], 'criterion':['gini', 'entropy'], 'min_samples_split':[5, 7, 9, 11, 13, 15]}
# 构建决策树分类器
model = DecisionTreeClassifier() # 这里因为要进行参数调优,所以不需要传入固定的参数了
# 网格搜索
grid_search = GridSearchCV(model, parameters, scoring='roc_auc', cv=5)
grid_search.fit(X_train, y_train)
# 获得参数的最优值
grid_search.best_params_
# 根据多参数调优的结果来重新搭建模型
model = DecisionTreeClassifier(criterion='entropy', max_depth=11, min_samples_split=13)
model.fit(X_train, y_train)
# 查看整体预测准确度
y_pred = model.predict(X_test)
from sklearn.metrics import accuracy_score
score = accuracy_score(y_pred, y_test)
print(score)
# 查看新的AUC值
# 预测不违约&违约概率
y_pred_proba = model.predict_proba(X_test)
y_pred_proba[:,1] # 如果想单纯的查看违约概率,即查看y_pred_proba的第二列
score = roc_auc_score(y_test, y_pred_proba[:,1])
print(score)
注意点1:多参数调优和分别单参数调优的区别
多参数调优和单参数分别调优是有区别的,比如有的读者为了省事,对上面的3个参数进行3次单独的单参数调优,然后将结果汇总,这样的做法其实是不严谨的。因为在进行单参数调优的时候,是默认其他参数取默认值的,那么该参数和其他参数都不取默认值的情况就没有考虑进来,也即忽略了多个参数对模型的组合影响。以上面的代码示例来说,使用多参数调优时,它是526=60种组合可能,而如果是进行3次单参数调优,则只是5+2+6=13种组合可能。 因此,如果只需要调节一个参数,那么可以使用单参数调优,如果需要调节多个参数,则推荐使用多参数调优。
注意点2:参数取值是给定范围的边界
另外一点需要需要注意的是,如果使用GridSearchCV()方法所得到的参数取值是给定范围的边界,那么有可能存在范围以外的取值使得模型效果更好,因此需要我们额外增加范围,继续调参。举例来说,倘若上述代码中获得的最佳max_depth值为设定的最大值13,那么实际真正合适的max_depth可能更大,此时便需要将搜索网格重新调整,如将max_depth的搜索范围变成[9, 11, 13, 15, 17],再重新参数调优。
参考文献:王宇韬, 钱妍竹. Python大数据分析与机器学习商业案例实战[M]. 机械工业出版社, 2020.