Python：蒙特卡洛算法以及三门问题

蒙特卡洛算法：

一 、蒙特卡洛算法简介

       蒙特·卡罗方法（Monte Carlo method），也称统计模拟方法，它是一种思想或者方法的统称，而不是严格意义上的算法。蒙特卡罗方法的起源是1777年由法国数学家布丰（Comte de Buffon）提出的用投针实验方法求圆周率，在20世纪40年代中期，由于计算机的发明结合概率统计理论的指导，从而正式总结为一种数值计算方法，其主要是用随机数来估算计算问题。

二、蒙特卡洛方法的基本思想

       当所求解问题是某种随机事件出现的概率，或者是某个随机变量的期望值时，通过某种“实验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个随机变量的某些数字特征，并将其作为问题的解。       

       假想你有一袋豆子，把豆子均匀地朝这个正方形上撒，然后数落在圆内的豆子数占正方形内豆子数的比例，即可计算出圆的面积，近而计算出π。而且当豆子越小，撒的越多的时候，结果就越精确。蒙特卡罗的理论依据是概率论中的大数定律。

三、蒙特卡洛算法的基本工作步骤

       蒙特卡罗算法一般分为三个步骤，分别为构造随机的概率的过程，从构造随机概率分布中抽样，求解估计量。

1.构造随机的概率过程
       对于本身就具有随机性质的问题，要正确描述和模拟这个概率过程。对于本来不是随机性质的确定性问题，比如计算定积分，就必须事先构造一个人为的概率过程了。它的某些参数正好是所要求问题的解，即要将不具有随机性质的问题转化为随机性质的问题。如本例中求圆周率的问题，是一个确定性的问题，需要事先构造一个概率过程，将其转化为随机性问题，即豆子落在圆内的概率，而π就是所要求的解。

2.从已知概率分布抽样
       由于各种概率模型都可以看作是由各种各样的概率分布构成的，因此产生已知概率分布的随机变量，就成为实现蒙特卡罗方法模拟实验的基本手段。如本例中采用的就是最简单、最基本的（0，1）上的均匀分布，而随机数是我们实现蒙特卡罗模拟的基本工具。

3.求解估计量
       实现模拟实验后，要确定一个随机变量，作为所要求问题的解，即无偏估计。建立估计量，相当于对实验结果进行考察，从而得到问题的解。如求出的近似π就认为是一种无偏估计。

四、样例:

sample1：蒙特卡洛方法求圆周率

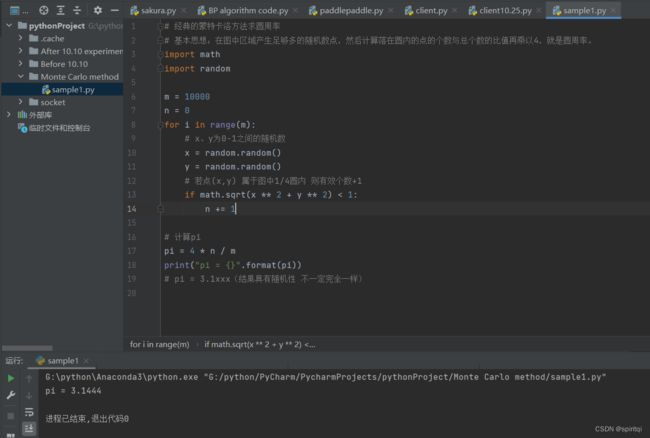
# 经典的蒙特卡洛方法求圆周率
# 基本思想：在图中区域产生足够多的随机数点，然后计算落在圆内的点的个数与总个数的比值再乘以4，就是圆周率。
import math
import random

m = 10000  #模拟次数为10000次
n = 0
for i in range(m):
    # x、y为0-1之间的随机数
    x = random.random()
    y = random.random()
    # 若点(x,y) 属于图中1/4圆内 则有效个数+1
    if math.sqrt(x ** 2 + y ** 2) < 1:
        n += 1
        
# 计算pi
pi = 4 * n / m
print("pi = {}".format(pi))
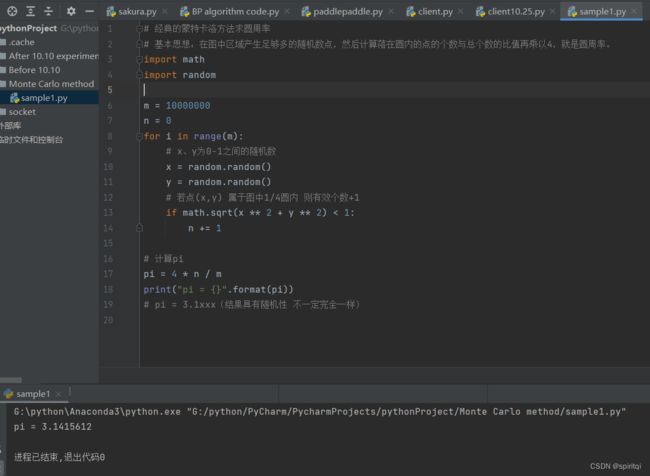
# pi = 3.1xxx（结果具有随机性 不一定完全一样）

 我们增加模拟次数，当模拟次数从10000次增加至10000000次时（即代码中m=10000改为m=10000000），π的值会更加精确。

 可见π的值从3.1444精确到了3.1415...

       除了上述方法，我们还可以借助计算机程序可以生成大量均匀分布的坐标点，接着统计出图形内的点数，通过它们占总点数的比例和坐标点生成范围的面积就可以求出的近似值。其内核思想相同，都是先产生随机点数然后通过计算图形内外点数所占比例来求出π的近似值。不同的只是下述代码更为直观地展现出来了。

import random
import math
import getopt
import sys
import matplotlib.pyplot as plt

def main():
    total = 0
    print('Start experiment: ')
    n = 0

 #Repeat try the estimate pi, until break it down manually
 while True:
        n=int(input(sys.argv))
 for i in range(n):
            x = random.uniform(-1,1)
            y = random.uniform(-1,1)
 #x^2 + y^2 <=1, means (x, y) in the cycle
 if math.sqrt(x ** 2 + y ** 2) <= 1.0:
                total += 1
                plt.plot(x, y, 'ro')
 # x^2 + y^2 > 1, means (x, y) out of the cycle
 else:
                plt.plot(x, y, 'b*')
        mypi = 4.0 * total / n
 #plot the x, y and close it after 5 seconds
        plt.ion()
        plt.pause(5)
        plt.close()

        print('Iteration Times = ', n, 'PI estimate value = ', mypi)
        print('math.pi = ', math.pi)
        print('Errors = ', abs(math.pi - mypi) / math.pi)

       用上述代码，我们用不同数量的随机点（100,100,0,10000）来计算π。实验结果如下。PIestimate 表示估计值，Errors表示与标准π的差。（注意这里的Errors是（π-PIestimate）/π）

 点数为100时：PIestimate= 3.1，Errors= 0.0132

 点数为1000时：PIestimate= 3.445，Errors= 0.0965

 点数为10000时：PIestimate= 3.478，Errors= 0.10708

 我们观察使用matplotlib.pyplot库绘出的图，并不是点数越多越精确，和我们日常生活中的直观感受大相径庭，原因其实是我们的点数没有达到某一个量级。一般情况下，蒙特卡洛算法的特点是，采样越多，越近似最优解，而永远不是最优解。

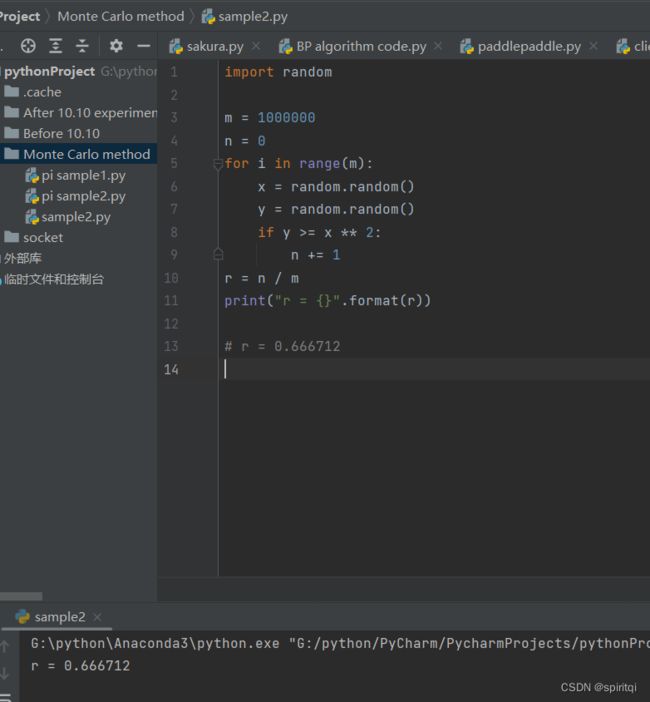
sample2：利用python计算函数y =  x^2在[0，1]区间的定积分

import random

m = 1000000
n = 0
for i in range(m):
    x = random.random()
    y = random.random()
    if y >= x ** 2:
        n += 1
r = n / m
print("r = {}".format(r))

# r = 0.666712

触类旁通：计算积分

 

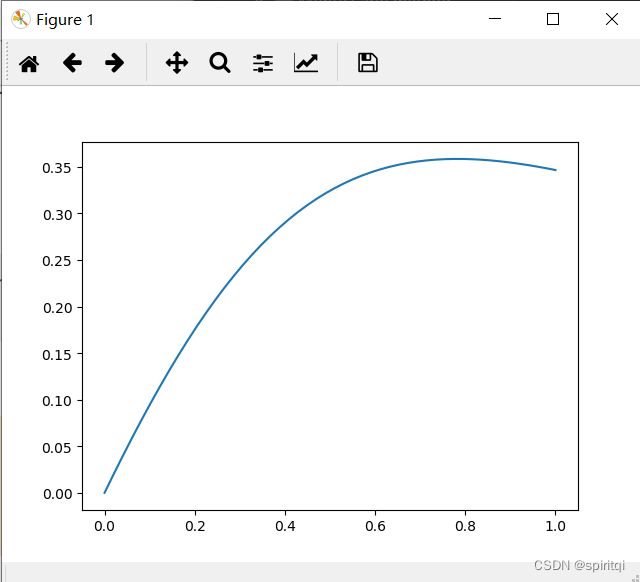
首先我们绘制函数图像：

import numpy as np
import matplotlib.pylab as plt

x = np.linspace(0, 1, num=50)
y = np.log(1 + x) / (1 + x ** 2)
plt.plot(x, y, '-')
plt.show()

 

计算积分：

import numpy as np
import random
m = 100000
n = 0
for i in range(m):
    x = random.random()
    y = random.random()
    if np.log(1 + x) / (1 + x**2) > y:
        n += 1
ans = n / m
print(ans)

# ans=0.27248  理论答案是 pi/8*log(2) = 0.2721983

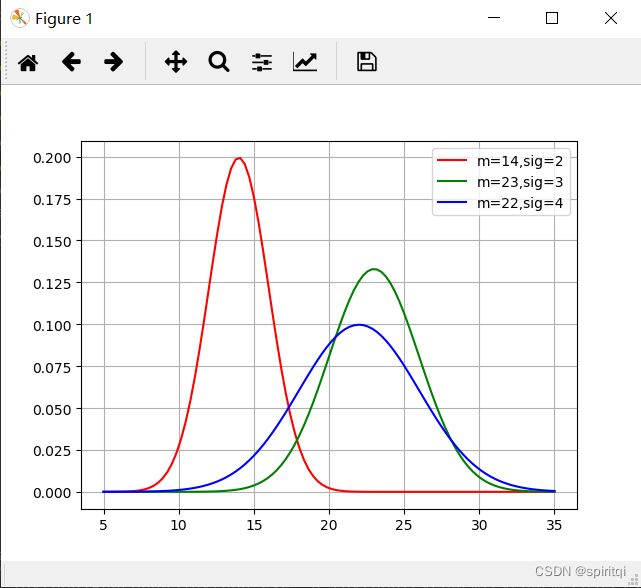
 sample3:

day_min=8，day_max=34. 我们设置时间范围为：5-35天

import numpy as np
import matplotlib.pyplot as plt
import math


def normal_distribution(x, mean, sigma):
    return np.exp(-1 * ((x - mean) ** 2) / (2 * (sigma ** 2))) / (math.sqrt(2 * np.pi) * sigma)


mean1, sigma1 = 14, 2
x1 = np.linspace(5, 35, num=100)

mean2, sigma2 = 23, 3
x2 = np.linspace(5, 35, num=100)

mean3, sigma3 = 22, 4
x3 = np.linspace(5, 35, num=100)

y1 = normal_distribution(x1, mean1, sigma1)
y2 = normal_distribution(x2, mean2, sigma2)
y3 = normal_distribution(x3, mean3, sigma3)

plt.plot(x1, y1, 'r', label='m=14,sig=2')
plt.plot(x2, y2, 'g', label='m=23,sig=3')
plt.plot(x3, y3, 'b', label='m=22,sig=4')
plt.legend()
plt.grid()
plt.show()

 

import numpy as np
import matplotlib.pylab as plt
import random
import math

m = 10000
a = 0
b = 0
y1 = np.random.normal(loc=14, scale=2, size=m)
y2 = np.random.normal(loc=23, scale=3, size=m)
y3 = np.random.normal(loc=22, scale=4, size=m)
y = y1 + y2 + y3
a, b = np.mean(y), np.var(y)
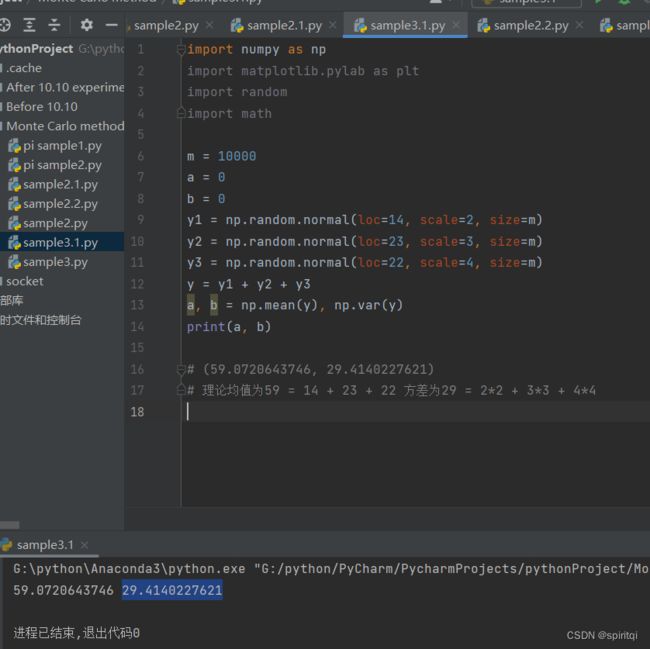
print(a, b)

# (59.0720643746, 29.4140227621)
# 理论均值为59 = 14 + 23 + 22 方差为29 = 2*2 + 3*3 + 4*4

三门问题：

一、三门问题的介绍：

       三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目Let's Make a Deal。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机率？如果严格按照上述的条件，即主持人清楚地知道，自己打开的那扇门后是羊，那么答案是会。不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是2/3。虽然该问题的答案在逻辑上并不自相矛盾，但十分违反直觉。

二、三门问题个人思考：

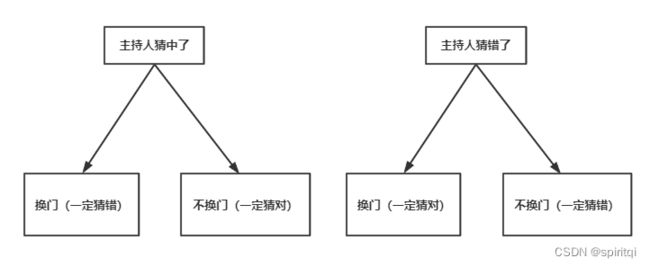
1.如果主持人事先知道门后情况（即主持人每次都能打开没有汽车的那扇门）：

（1）玩家不换策略，则玩家的中奖概率为1/3（主持人开门的环节对玩家没影响，长期来看中奖概率必为1/3）；

（2）玩家更换策略，则玩家的中奖概率为2/3（相当于玩家一开始就选中了另两扇门，主持人出来帮忙排除了一扇门，长期来看中奖概率必为2/3）。
2.如果主持人事先不知道门后情况（即主持人是随机打开一扇门，可能会打开有汽车的那扇门，则游戏终结），则玩家换策略与不换策略的中奖概率均为1/2。

三、图解：

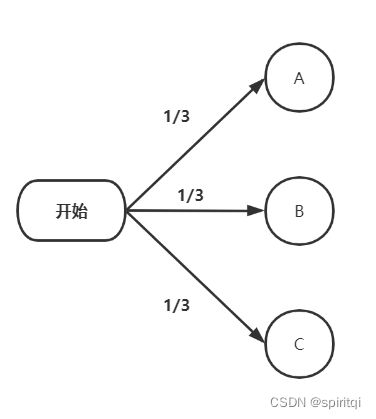
1.参与者第一次选择：

       首先，我们要假设参赛者在第一次选择的时候，没有任何先验知识可以参考，也就是说，他不掌握任何辅助选择的有效信息，所以，我们可以认为这是个随机选择，即参赛者选中任一扇门的可能性都是相等的，都是1/3。

如下图示:

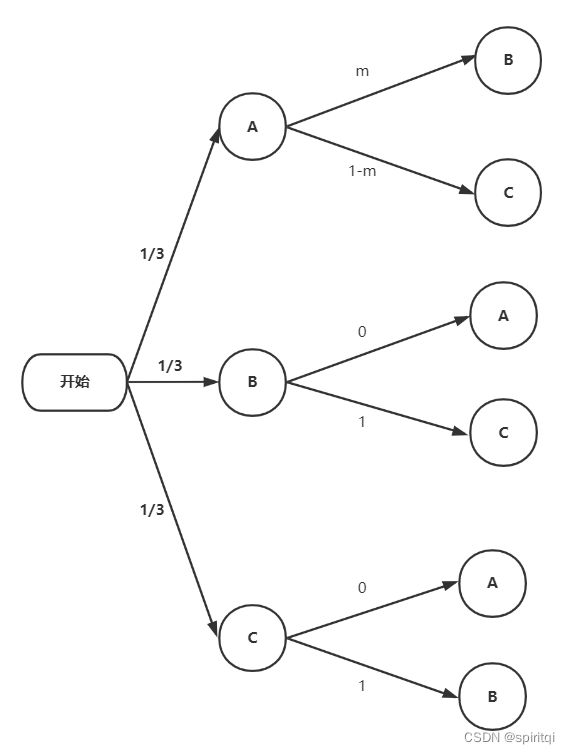
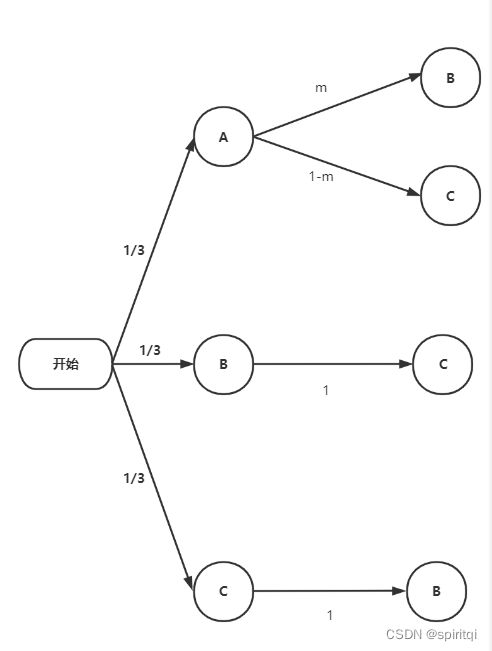
2.主持人的选择：

       可以分成三种情况，分别是车子在A门、B门和C门后，当我们得到车子在A门后的条件下的概率是a的话，因为参赛者是随机选择，那么其他两种情况的概率也是a，所以，根据全概率公式，总的概率就是 1/3 * a + 1/3 * a + 1/3 * a = a 所以，假设车子在A门后面，分析得到的结果，就是最终结果。       

       主持人选择的可能性如下图示。如果参赛者第一次选了A门，那么主持人可能会随意的打开B门或者C门，不妨记可能性为m和1-m。如果参赛者第一次选了B门的话，那么，主持人选择A门打开的可能性为0，只能打开C门，所以其可能性为1。如果参赛者选了C门的条件下，主持人只能打开B门。

       一旦出现了概率为0的箭头，这就意味着这种情况不会发生，后续的可能性都不会再从这种情况衍生，所以，我们可以将上图简化为如下所示。

 注意上述情况的前提都是车子在A门后

3.参与者的第二次选择：

      参赛者的第二次选择，有两种方案，一是维持原先的选择，二是更改选择。

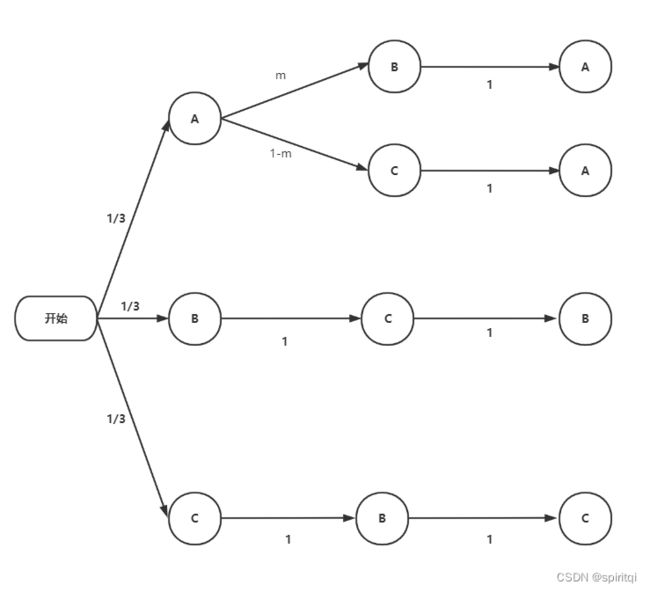
3.1 维持原先的选择

根据全概率公式，参与者选中车（即选择A门）的概率是：
1/3 * m * 1 + 1/3 * (1-m) * 1 = 1/3

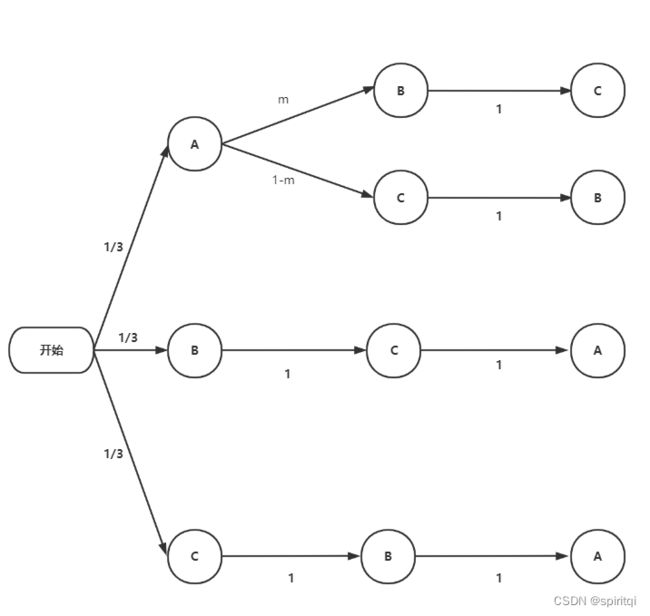
3.2 更改原先的选择

       由于一共就三个门，更改选择的话，也只有唯一的选择，所以，此时图中新加事情的可能性也是100%，如下图所示。

根据全概率公式，参与者选中车（即选择A门）的概率是：
1/3 * 1 * 1 + 1/3 * 1 * 1 = 2/3

由于三分之二 > 三分之一，所以结论为更改选择可以提高选中概率。

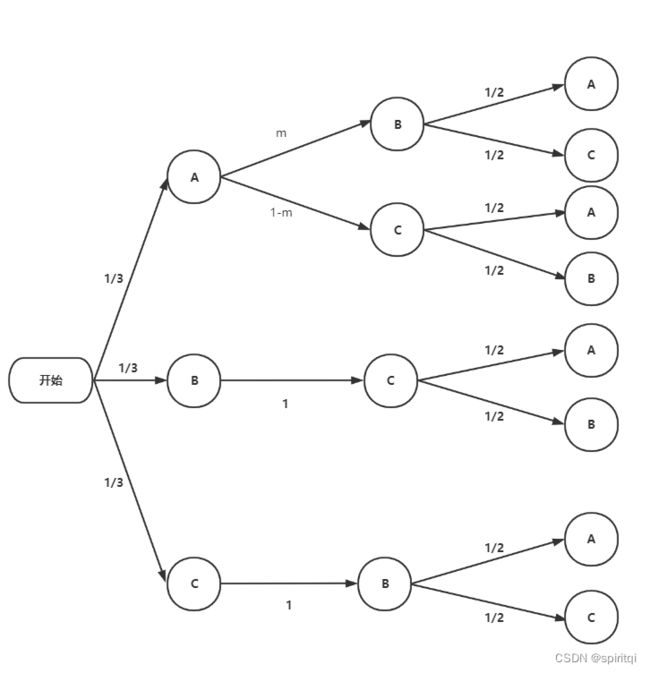
4.我们的分析中50%概率： 
        如果，在主持人打开一扇门后，新来一个参赛者，他并不知道先前发生的事情，面对剩下的两扇门做随机选择，显然，他选中A门的概率是50%，而前面的分析知道维持选择和更改选择的概率分别是1/3和2/3。

所以，新参赛者选中车（即选择A门）的概率是：
1/3 * m * 1/2 + 1/3 x (1-m) x 1/2 + 1/3 x 1 x 1/2 + 1/3 x 1 x 1/2 = 50%

四、蒙特卡洛过程：

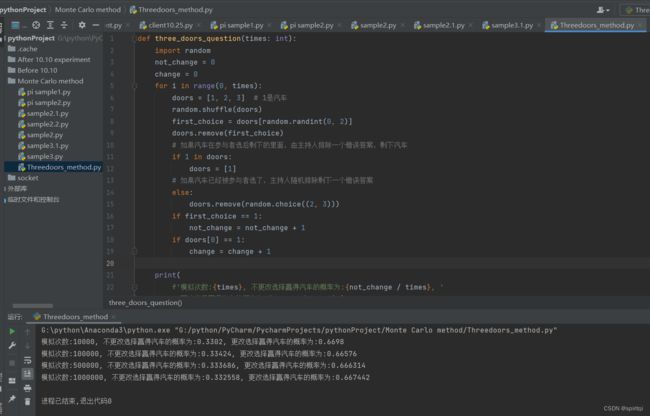
 python编程实现：

def three_doors_question(times: int):
    import random
    not_change = 0
    change = 0
    for i in range(0, times):
        doors = [1, 2, 3]  # 1是汽车
        random.shuffle(doors)
        first_choice = doors[random.randint(0, 2)]
        doors.remove(first_choice)
        # 如果汽车在参与者选后剩下的里面，由主持人排除一个错误答案，剩下汽车
        if 1 in doors:
            doors = [1]
        # 如果汽车已经被参与者选了，主持人随机排除剩下一个错误答案
        else:
            doors.remove(random.choice((2, 3)))
        if first_choice == 1:
            not_change = not_change + 1
        if doors[0] == 1:
            change = change + 1

    print(
        f'模拟次数:{times}, 不更改选择赢得汽车的概率为:{not_change / times}, '
        f'更改选择赢得汽车的概率为:{change / times}')


three_doors_question(10000)
three_doors_question(100000)
three_doors_question(500000)
three_doors_question(1000000)

 运行截图：