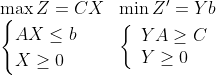Python数学建模—线性规划
我是猿童学,本文是根据司守奎老师《数学建模算法与程序》的书本内容编写,使用其书中案例,书中的编程语言是MATLAB、Lingo,我将使用Python来解决问题。接下来的一个月我将学习使用Python来解决数学建模问题。将记录下学习中的笔记和部分案例。
1、线性规划
1.1 线性规划的实例与定义
例 1 某机床厂生产甲、乙两种机床每台销售后的利润分别为 4000 元与3000元。 生产甲机床需用 A、B 机器加工,加工时间分别为每台 2 小时和1小时生产乙机床需用 A、B、C 三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时数分别为 A 机器 10 小时、B 机器 8 小时和C 机器 7 小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
上述问题的数学模型:设该厂生产 ![]() 台甲机床和
台甲机床和![]() 乙机床时总利润最大,则
乙机床时总利润最大,则![]() 应满足:
应满足:
![]()
这里变量 ![]() 称之为决策变量,(1)式被称为问题的目标函数,(2)中的几个不等式 是问题的约束条件,记为 s.t.(即 subject to)。由于上面的目标函数及约束条件均为线性 函数,故被称为线性规划问题。总之,线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最 小的问题。
称之为决策变量,(1)式被称为问题的目标函数,(2)中的几个不等式 是问题的约束条件,记为 s.t.(即 subject to)。由于上面的目标函数及约束条件均为线性 函数,故被称为线性规划问题。总之,线性规划问题是在一组线性约束条件的限制下,求一线性目标函数最大或最 小的问题。
1.2 使用Python中的scipy库求解列 1 线性规划问题:
线性规划的标准型为
![]() (3)
(3)
其中,c是价值向量;A和b对应线性不等式约束;Aeq和beq对应线性等式约束;bounds对应公式中的lb和ub,决策向量的下界和上界。
scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='simplex', callback=None, options=None)
输入参数解析:
- c:线性目标函数的系数
- A_ub(可选参数):不等式约束矩阵,
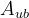 的每一行指定x上的线性不等式约束的系数
的每一行指定x上的线性不等式约束的系数 - b_ub(可选参数):不等式约束向量,每个元素代表
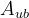 x的上限
x的上限 - A_eq(可选参数):等式约束矩阵,
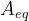 的每一行指定x xx上的线性等式约束的系数
的每一行指定x xx上的线性等式约束的系数 - b_eq(可选参数):等式约束向量,
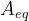 的每个元素必须等于
的每个元素必须等于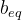 的对应元素
的对应元素 - bounds(可选参数):定义决策变量x的最小值和最大值
- 数据类型: (min, max)序列对
- None:使用None表示没有界限,默认情况下,界限为(0,None)(所有决策变量均为非负数)
- 如果提供一个元组(min, max),则最小值和最大值将用作所有决策变量的界限。
输出参数解析:
- x:在满足约束的情况下将目标函数最小化的决策变量的值
- fun:目标函数的最优值(
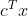 )
) - slack:不等式约束的松弛值(名义上为正值)
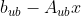
- con:等式约束的残差(名义上为零)
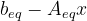
- success:当算法成功找到最佳解决方案时为 True
- status:表示算法退出状态的整数
- 0 : 优化成功终止
- 1 : 达到了迭代限制
- 2 : 问题似乎不可行
- 3 : 问题似乎是不收敛
- 4 : 遇到数值困难
- nit:在所有阶段中执行的迭代总数
- message:算法退出状态的字符串描述符
使用scipy库来解决例1:
from scipy.optimize import linprog
c = [-4, -3] #目标函数的系数
A= [[2, 1], [1, 1],[0,1]] #<=不等式左侧未知数系数矩阵
b = [10,8,7] # <=不等式右侧常数矩阵
#A_eq = [[]] #等式左侧未知数系数矩阵
#B_eq = [] #等式右侧常数矩阵
x1 = [0, None] #未知数取值范围
x2 = [0, None] #未知数取值范围
res =linprog(c, A, b, bounds=(x1, x2))#默认求解最小值,求解最大值使用-c并取结果相反数
print(res)
输出结果:
con: array([], dtype=float64)
fun: -25.999999999841208
message: 'Optimization terminated successfully.'
nit: 5
slack: array([8.02629074e-11, 3.92663679e-11, 1.00000000e+00])
status: 0
success: True
x: array([2., 6.])fun为目标函数的最优值,slack为松弛变量,status表示优化结果状态,x为最优解。
此模型的求解结果为:当x1=2,x2=6时,函数取得最优值25.999999999841208。
例 2 求解下列线性规划问题:
注意要先标准化!
这里使用另一种比较规范的写法:
from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
B = np.array([-10,12])
Aeq = np.array([[1,1,1]])
Beq = np.array([7])
x1 = [0, None] #未知数取值范围
x2 = [0, None] #未知数取值范围
x3 = [0, None] #未知数取值范围
res = optimize.linprog(-c,A,B,Aeq,Beq,bounds=(x1, x2, x3))
print(res)输出结果:
con: array([1.80713489e-09])
fun: -14.571428565645054
message: 'Optimization terminated successfully.'
nit: 5
slack: array([-2.24579466e-10, 3.85714286e+00])
status: 0
success: True
x: array([6.42857143e+00, 5.71428571e-01, 2.35900788e-10])此模型的求解结果为:当x1=6.4,x2=5.7,x3=2.3时,函数取得最优值14.571428565645054
例3 求解线性规划问题:
使用Python编写:
from scipy import optimize
import numpy as np
c = np.array([2,3,1])
A = np.array([[1,4,2],[3,2,0]])
B = np.array([8,6])
x1 = [0, None] #未知数取值范围
x2 = [0, None] #未知数取值范围
x3 = [0, None] #未知数取值范围
res = optimize.linprog(c,-A,-B,bounds=(x1, x2, x3))
print(res)
输出结果:
con: array([], dtype=float64)
fun: 6.999999994872993
message: 'Optimization terminated successfully.'
nit: 3
slack: array([ 3.85261245e-09, -1.41066261e-08])
status: 0
success: True
x: array([1.17949641, 1.23075538, 0.94874104])此模型的求解结果为:当x1=1.1,x2=1.2,x3=0.9时,函数取得最优值6.999999994872993
2、运输问题
2.1产销平衡的数学建模过程:
例 6 某商品有![]() 个产地、
个产地、![]() 个销地,各产地的产量分别为
个销地,各产地的产量分别为![]() ,各销地的需求量分别为
,各销地的需求量分别为![]() 。若该商品由
。若该商品由 ![]() 产地运到
产地运到 ![]() 销地的单位运价为
销地的单位运价为![]() ,问应该如何调运才能使总运费最省?
,问应该如何调运才能使总运费最省?
解:引入变量 ![]() ,其取值为由
,其取值为由 ![]() 产地运往
产地运往 ![]() 销地的该商品数量,数学模型为
销地的该商品数量,数学模型为
显然是一个线性规划问题,当然可以用单纯形法求解。
对产销平衡的运输问题,由于有以下关系式存在:
其约束条件的系数矩阵相当特殊,可用比较简单的计算方法,习惯上称为表上作业法(由 康托洛维奇和希奇柯克两人独立地提出,简称康—希表上作业法),下面使用例子来讲解。
2.2 产销平衡的运输问题
1.问题描述
某公司下属有甲、乙、丙三个工厂,分别向A、B、C、D四个销地提供产品,产量、需求量及工厂到销售地的运价(单位:元/吨)如下表所示,求使费用最少的最佳运输方案。
| 工厂 \ 销地 | A | B | C | D | 产量(吨) |
| 甲 | 8 | 6 | 10 | 9 | 18 |
| 乙 | 9 | 12 | 13 | 1 | 18 |
| 丙 | 14 | 12 | 16 | 5 | 19 |
| 销量(吨) | 16 | 15 | 7 | 17 | 55 |
2.问题解析
总产量=18+18+19=55
总销量=16+15+7+17=55
产量等于销量,即这是产销平衡的运输问题。直接采用表上作业法进行求解。
3.使用python求解:
# 运输问题求解:使用Vogel逼近法寻找初始基本可行解
import numpy as np
import copy
import pandas as pd
def main():
# mat = pd.read_csv('表上作业法求解运输问题.csv', header=None).values
# mat = pd.read_excel('表上作业法求解运输问题.xlsx', header=None).values
a = np.array([18, 18, 19]) # 产量
b = np.array([16, 15, 7, 17]) # 销量
c = np.array([[8, 6, 10, 9], [9, 12, 13, 7], [14, 12, 16, 5]])
# [c, x] = TP_vogel(mat)
[c,x]=TP_vogel([c,a,b])
def TP_split_matrix(mat): # 运输分割矩阵
c = mat[:-1, :-1]
a = mat[:-1, -1]
b = mat[-1, :-1]
return (c, a, b)
def TP_vogel(var): # Vogel法代码,变量var可以是以numpy.ndarray保存的运输表,或以tuple或list保存的(成本矩阵,供给向量,需求向量)
import numpy
typevar1 = type(var) == numpy.ndarray
typevar2 = type(var) == tuple
typevar3 = type(var) == list
if typevar1 == False and typevar2 == False and typevar3 == False:
print('>>>非法变量<<<')
(cost, x) = (None, None)
else:
if typevar1 == True:
[c, a, b] = TP_split_matrix(var)
elif typevar2 == True or typevar3 == True:
[c, a, b] = var
cost = copy.deepcopy(c)
x = np.zeros(c.shape)
M = pow(10, 9)
for factor in c.reshape(1, -1)[0]:
p = 1
while int(factor) != M:
if np.all(c == M):
break
else:
print('第1次迭代!')
print('c:\n', c)
# 获取行/列最小值数组
row_mini1 = []
row_mini2 = []
for row in range(c.shape[0]):
Row = list(c[row, :])
row_min = min(Row)
row_mini1.append(row_min)
Row.remove(row_min)
row_2nd_min = min(Row)
row_mini2.append(row_2nd_min)
# print(row_mini1,'\n',row_mini2)
r_pun = [row_mini2[i] - row_mini1[i] for i in range(len(row_mini1))]
print('行罚数:', r_pun)
# 计算列罚数
col_mini1 = []
col_mini2 = []
for col in range(c.shape[1]):
Col = list(c[:, col])
col_min = min(Col)
col_mini1.append(col_min)
Col.remove(col_min)
col_2nd_min = min(Col)
col_mini2.append(col_2nd_min)
c_pun = [col_mini2[i] - col_mini1[i] for i in range(len(col_mini1))]
print('列罚数:', c_pun)
pun = copy.deepcopy(r_pun)
pun.extend(c_pun)
print('罚数向量:', pun)
max_pun = max(pun)
max_pun_index = pun.index(max(pun))
max_pun_num = max_pun_index + 1
print('最大罚数:', max_pun, '元素序号:', max_pun_num)
if max_pun_num <= len(r_pun):
row_num = max_pun_num
print('对第', row_num, '行进行操作:')
row_index = row_num - 1
catch_row = c[row_index, :]
print(catch_row)
min_cost_colindex = int(np.argwhere(catch_row == min(catch_row)))
print('最小成本所在列索引:', min_cost_colindex)
if a[row_index] <= b[min_cost_colindex]:
x[row_index, min_cost_colindex] = a[row_index]
c1 = copy.deepcopy(c)
c1[row_index, :] = [M] * c1.shape[1]
b[min_cost_colindex] -= a[row_index]
a[row_index] -= a[row_index]
else:
x[row_index, min_cost_colindex] = b[min_cost_colindex]
c1 = copy.deepcopy(c)
c1[:, min_cost_colindex] = [M] * c1.shape[0]
a[row_index] -= b[min_cost_colindex]
b[min_cost_colindex] -= b[min_cost_colindex]
else:
col_num = max_pun_num - len(r_pun)
col_index = col_num - 1
print('对第', col_num, '列进行操作:')
catch_col = c[:, col_index]
print(catch_col)
# 寻找最大罚数所在行/列的最小成本系数
min_cost_rowindex = int(np.argwhere(catch_col == min(catch_col)))
print('最小成本所在行索引:', min_cost_rowindex)
# 计算将该位置应填入x矩阵的数值(a,b中较小值)
if a[min_cost_rowindex] <= b[col_index]:
x[min_cost_rowindex, col_index] = a[min_cost_rowindex]
c1 = copy.deepcopy(c)
c1[min_cost_rowindex, :] = [M] * c1.shape[1]
b[col_index] -= a[min_cost_rowindex]
a[min_cost_rowindex] -= a[min_cost_rowindex]
else:
x[min_cost_rowindex, col_index] = b[col_index]
# 填入后删除已满足/耗尽资源系数的行/列,得到剩余的成本矩阵,并改写资源系数
c1 = copy.deepcopy(c)
c1[:, col_index] = [M] * c1.shape[0]
a[min_cost_rowindex] -= b[col_index]
b[col_index] -= b[col_index]
c = c1
print('本次迭代后的x矩阵:\n', x)
print('a:', a)
print('b:', b)
print('c:\n', c)
if np.all(c == M):
print('【迭代完成】')
print('-' * 60)
else:
print('【迭代未完成】')
print('-' * 60)
p += 1
print(f"第{p}次迭代!")
total_cost = np.sum(np.multiply(x, cost))
if np.all(a == 0):
if np.all(b == 0):
print('>>>供求平衡<<<')
else:
print('>>>供不应求,需求方有余量<<<')
elif np.all(b == 0):
print('>>>供大于求,供给方有余量<<<')
else:
print('>>>无法找到初始基可行解<<<')
print('>>>初始基本可行解x*:\n', x)
print('>>>当前总成本:', total_cost)
[m, n] = x.shape
varnum = np.array(np.nonzero(x)).shape[1]
if varnum != m + n - 1:
print('【注意:问题含有退化解】')
return (cost, x)
if __name__ == '__main__':
main()输出结果:
D:\Anaconda\python.exe D:/PyCharm/数学建模/线性规划/www.py
第1次迭代!
c:
[[ 8 6 10 9]
[ 9 12 13 7]
[14 12 16 5]]
行罚数: [2, 2, 7]
列罚数: [1, 6, 3, 2]
罚数向量: [2, 2, 7, 1, 6, 3, 2]
最大罚数: 7 元素序号: 3
对第 3 行进行操作:
[14 12 16 5]
最小成本所在列索引: 3
本次迭代后的x矩阵:
[[ 0. 0. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [18 18 2]
b: [16 15 7 0]
c:
[[ 8 6 10 1000000000]
[ 9 12 13 1000000000]
[ 14 12 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第2次迭代!
第1次迭代!
c:
[[ 8 6 10 1000000000]
[ 9 12 13 1000000000]
[ 14 12 16 1000000000]]
行罚数: [2, 3, 2]
列罚数: [1, 6, 3, 0]
罚数向量: [2, 3, 2, 1, 6, 3, 0]
最大罚数: 6 元素序号: 5
对第 2 列进行操作:
[ 6 12 12]
最小成本所在行索引: 0
本次迭代后的x矩阵:
[[ 0. 15. 0. 0.]
[ 0. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [ 3 18 2]
b: [16 0 7 0]
c:
[[ 8 1000000000 10 1000000000]
[ 9 1000000000 13 1000000000]
[ 14 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第3次迭代!
第1次迭代!
c:
[[ 8 1000000000 10 1000000000]
[ 9 1000000000 13 1000000000]
[ 14 1000000000 16 1000000000]]
行罚数: [2, 4, 2]
列罚数: [1, 0, 3, 0]
罚数向量: [2, 4, 2, 1, 0, 3, 0]
最大罚数: 4 元素序号: 2
对第 2 行进行操作:
[ 9 1000000000 13 1000000000]
最小成本所在列索引: 0
本次迭代后的x矩阵:
[[ 0. 15. 0. 0.]
[16. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [3 2 2]
b: [0 0 7 0]
c:
[[1000000000 1000000000 10 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第4次迭代!
第1次迭代!
c:
[[1000000000 1000000000 10 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
行罚数: [999999990, 999999987, 999999984]
列罚数: [0, 0, 3, 0]
罚数向量: [999999990, 999999987, 999999984, 0, 0, 3, 0]
最大罚数: 999999990 元素序号: 1
对第 1 行进行操作:
[1000000000 1000000000 10 1000000000]
最小成本所在列索引: 2
本次迭代后的x矩阵:
[[ 0. 15. 3. 0.]
[16. 0. 0. 0.]
[ 0. 0. 0. 17.]]
a: [0 2 2]
b: [0 0 4 0]
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第5次迭代!
第1次迭代!
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 13 1000000000]
[1000000000 1000000000 16 1000000000]]
行罚数: [0, 999999987, 999999984]
列罚数: [0, 0, 3, 0]
罚数向量: [0, 999999987, 999999984, 0, 0, 3, 0]
最大罚数: 999999987 元素序号: 2
对第 2 行进行操作:
[1000000000 1000000000 13 1000000000]
最小成本所在列索引: 2
本次迭代后的x矩阵:
[[ 0. 15. 3. 0.]
[16. 0. 2. 0.]
[ 0. 0. 0. 17.]]
a: [0 0 2]
b: [0 0 2 0]
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 16 1000000000]]
【迭代未完成】
------------------------------------------------------------
第6次迭代!
第1次迭代!
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 16 1000000000]]
行罚数: [0, 0, 999999984]
列罚数: [0, 0, 999999984, 0]
罚数向量: [0, 0, 999999984, 0, 0, 999999984, 0]
最大罚数: 999999984 元素序号: 3
对第 3 行进行操作:
[1000000000 1000000000 16 1000000000]
最小成本所在列索引: 2
本次迭代后的x矩阵:
[[ 0. 15. 3. 0.]
[16. 0. 2. 0.]
[ 0. 0. 2. 17.]]
a: [0 0 0]
b: [0 0 0 0]
c:
[[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]
[1000000000 1000000000 1000000000 1000000000]]
【迭代完成】
------------------------------------------------------------
>>>供求平衡<<<
>>>初始基本可行解x*:
[[ 0. 15. 3. 0.]
[16. 0. 2. 0.]
[ 0. 0. 2. 17.]]
>>>当前总成本: 407.0
进程已结束,退出代码为 0
上面使用的方法是表上作业法,属下所示:
最终最优的总成本: 407.0
2.3 产大于销的运输问题
1.问题描述
有三个牧业基地向4个城市提供鲜奶,4个城市每日的鲜奶需求量、3个基地的每日鲜奶供应量以及运送每千升鲜奶的费用如下表所示,试确定最经济的鲜奶运输方案。
| 城市\基地 | A | B | c | D | 供应量 |
| 甲 | 3 | 2 | 4 | 5 | 30 |
| 乙 | 2 | 3 | 5 | 3 | 40 |
| 丙 | 1 | 4 | 2 | 4 | 50 |
| 需求量 | 16 | 30 | 24 | 30 |
2.问题解析
总供应量=30+40+50=120
总需求量=16+30+24+30=100
供过于求,即产量大于销量,这是一个产大于销的运输问题。要将问题转化为产销平衡的运输问题,需进行以下几个方面的调整。
(1)增加一个虚拟销地E,使其总需求量为120-100=20。
(2)由于销地是虚拟的,实际上是产量过剩的物资在产地就地储存,所以不会产生实际的运输,即不会产生运费。
因此新的供需量及单位运价表如下所示。
| 城市\基地 | A | B | c | D | E | 供应量 |
| 甲 | 3 | 2 | 4 | 5 | 0 | 30 |
| 乙 | 2 | 3 | 5 | 3 | 0 | 40 |
| 丙 | 1 | 4 | 2 | 4 | 0 | 50 |
| 需求量 | 16 | 30 | 24 | 30 | 20 | 120 |
3.问题求解
使用python来实现:
这里也可以使用(最小元素法)来解决:
'----------------------------------------最小元素法------------------------------------' \
'最小元素法是指有限满足单位运价最小的供销服务'
import numpy as np
import copy
supplyNum = 3 # 供应商数量
demandNum = 5 # 需求商数量
A = np.array([30,40,50]) # 产量
B = np.array([16,30,24,30,20]) # 销量
C = np.array([[3,2,4,5,0], [2,3,5,3,0], [1,4,2,4,0]]) # 成本
X = np.zeros((supplyNum, demandNum)) # 初始解
c = copy.deepcopy(C)
maxNumber = 10000 # 极大数
def pivot(A, B, c, X):
index = np.where(c == np.min(c)) # 寻找最小值的索引
minIndex = (index[0][0], index[1][0]) # 确定最小值的索引
# 确定应该优先分配的量,并且改变价格
if A[index[0][0]] > B[index[1][0]]:
X[minIndex] = B[index[1][0]]
c[:, index[1][0]] = maxNumber # 改变价格
A[index[0][0]] = A[index[0][0]] - B[index[1][0]]
B[index[1][0]] = 0 # 改变销量
else:
X[minIndex] = A[index[0][0]]
c[index[0][0], :] = maxNumber
B[index[1][0]] = B[index[1][0]] - A[index[0][0]]
A[index[0][0]] = 0
return A, B, c, X
# 最小元素法
def minimumElementMethod(A, B, c, X):
while (c < maxNumber).any():
A, B, c, X = pivot(A, B, c, X)
return X
solutionMin = minimumElementMethod(A, B, c, X)
print('最小元素法得到的初始解为:')
print(solutionMin)
print('最小元素法得到的总运费为:', ((solutionMin * C).sum()))
输出结果:
最小元素法得到的初始解为:
[[ 0. 10. 0. 0. 20.]
[ 0. 20. 0. 20. 0.]
[16. 0. 24. 10. 0.]]
最小元素法得到的总运费为: 244.02.4 产小于销的运输问题
1.问题描述
某三个煤炭厂供应4个地区,假定等量的煤炭在这些地区使用效果相同,已知各煤炭厂年产量,各地区的需要量及从各煤炭厂到各地区的单位运价表如下所示,试决定最优的调运方案。
| 销地\产地 | B1 | B2 | B3 | B4 | 产量 |
| A1 | 5 | 3 | 10 | 4 | 90 |
| A2 | 2 | 6 | 9 | 6 | 40 |
| A3 | 14 | 10 | 5 | 7 | 70 |
| 销量 | 30 | 50 | 100 | 40 |
2.问题解析
总供应量=30+40+50=120
总需求量=16+30+24+30=100
供过于求,即产量大于销量,这是一个产大于销的运输问题。要将问题转化为产销平衡的运输问题,需进行以下几个方面的调整。
(1)增加一个虚拟销地E,使其总需求量为120-100=20。
(2)由于销地是虚拟的,实际上是产量过剩的物资在产地就地储存,所以不会产生实际的运输,即不会产生运费。
因此新的供需量及单位运价表如下所示。
| 销地\产地 | B | B | B3 | B4 | 产量 |
| A, | 5 | 3 | 10 | 4 | 90 |
| A2 | 2 | 6 | 9 | 6 | 40 |
| A3 | 14 | 10 | 5 | 7 | 70 |
| A4 | 0 | 0 | 0 | 0 | 20 |
| 销量 | 30 | 50 | 100 | 40 | 220 |
3.问题求解
使用python求解:
这里可以使用(Vogel逼近法)寻找初始基本可行解
'-----------------------------------Vogel法---------------------------------'
supplyNum = 4 # 供应商数量
demandNum = 4 # 需求商数量
A = np.array([90,40,70,20]) # 产量
B = np.array([30,50,100,40]) # 销量
C = np.array([[5,3,10,4], [2,6,9,6], [14,10,5,7],[0,0,0,0]]) # 成本
X = np.zeros((supplyNum, demandNum)) # 初始解
c = copy.deepcopy(C)
numPunish = [0] * (supplyNum + demandNum) # 整体罚数
def pivot(X, A, B, C):
# 求解罚数,其中列罚数排在行罚数后面
for i in range(supplyNum):
sortList = np.sort(C[i, :])
numPunish[i] = sortList[1] - sortList[0]
for i in range(demandNum):
sortList = np.sort(C[:, i])
numPunish[i + supplyNum] = sortList[1] - sortList[0]
maxIndex = np.argmax(numPunish) # 寻找最大罚数的索引
# 若最大的罚数属于行罚数
if maxIndex < supplyNum:
minIndex = np.argmin(C[maxIndex, :])
index = (maxIndex, minIndex) # 得到最大罚数的一行中最小的运价
# 若产量大于销量
if A[maxIndex] > B[minIndex]:
X[index] = B[minIndex] # 更新解
C[:, minIndex] = maxNumber # 将已经满足的一列中的运价增大替代删除操作
A[maxIndex] -= B[minIndex] # 更新剩余产量
B[minIndex] = 0 # 更新已经满足的销量
# 若销量大于产量
else:
X[index] = A[maxIndex]
C[maxIndex, :] = maxNumber
B[minIndex] -= A[maxIndex] # 更新销量
A[maxIndex] = 0
# 若最大的罚数为列罚数
else:
minIndex = np.argmin(C[:, maxIndex - supplyNum]) # 这时maxIndex-supplyNum是罚数最大的列
index = (minIndex, maxIndex - supplyNum)
if A[minIndex] > B[maxIndex - supplyNum]: # 这里是产量大于销量,因此有限满足销量
X[index] = B[maxIndex - supplyNum]
C[:, maxIndex - supplyNum] = maxNumber
A[minIndex] -= B[maxIndex - supplyNum]
B[maxIndex - supplyNum] = 0
else:
X[index] = A[minIndex]
C[minIndex, :] = maxNumber
B[maxIndex - supplyNum] -= A[minIndex]
A[minIndex] = 0
return X, A, B, C
# 沃格尔法得到初始解
def Vogel(A, B, C):
X = np.zeros((supplyNum, demandNum)) # 初始解
numPunish = [0] * (supplyNum + demandNum) # 整体罚数
# 迭代,直到所有的产量和销量全部满足
while (A != 0).any() and (B != 0).any():
X, A, B, C = pivot(X, A, B, C)
return X
# 上面对于条件的判断,还需要对销量和需求量进行改变
solutionVogel = Vogel(A, B, c)
print('Vogel法得到的初始解为:')
print(solutionVogel)
print('Vogel法得到的总运费为:', (C * solutionVogel).sum())输出结果:
Vogel法得到的初始解为:
[[ 0. 50. 0. 40.]
[30. 0. 10. 0.]
[ 0. 0. 70. 0.]
[ 0. 0. 20. 0.]]
Vogel法得到的总运费为: 810.0上面三种产销问题是常见的情况,除了产销问题还有弹性需求的运输问题、中间转运的运输问题。
这里就不罗嗦了,自己查资料噢!
3、指派问题
3.1 指派问题的数学模型
例 7 拟分配 ![]() 人去干
人去干 ![]() 项工作,每人干且仅干一项工作,若分配第
项工作,每人干且仅干一项工作,若分配第 ![]() 人去干第
人去干第 ![]() 项工作,需花费
项工作,需花费 ![]() 单位时间,问应如何分配工作才能使工人花费的总时间最少?
单位时间,问应如何分配工作才能使工人花费的总时间最少?
容易看出,要给出一个指派问题的实例,只需给出矩阵![]() ,
, ![]() 被称为指派 问题的系数矩阵。 引入变量
被称为指派 问题的系数矩阵。 引入变量 ![]() ,若分配
,若分配 ![]() 干
干 ![]() 工作,则取
工作,则取 ![]() = 1,否则取
= 1,否则取 ![]() = 0 。上述指派问题的数学模型为:
= 0 。上述指派问题的数学模型为:
述指派问题的可行解可以用一个矩阵表示,其每行每列均有且只有一个元素为 1,其余元素均为 0;可以用![]() 中的一个置换表示。
中的一个置换表示。
问题中的变量只能取 0 或 1,从而是一个 0-1 规划问题。一般的 0-1 规划问题求解 极为困难。但指派问题并不难解,其约束方程组的系数矩阵十分特殊(被称为全单位模矩阵,其各阶非零子式均为 ±1),其非负可行解的分量只能取 0 或 1,故约束 ![]() = 0或1 可改写为
= 0或1 可改写为 ![]() ≥ 0而不改变其解。此时,指派问题被转化为一个特殊的运输问题,其中
≥ 0而不改变其解。此时,指派问题被转化为一个特殊的运输问题,其中 ![]() ,
,![]() 。
。
3.2 求解指派问题的匈牙利算法
算法主要依据以下事实:如果系数矩阵 ![]() 一行(或一列)中每 一元素都加上或减去同一个数,得到一个新矩阵
一行(或一列)中每 一元素都加上或减去同一个数,得到一个新矩阵 ![]() ,则以C 或 B 为系数矩阵的 指派问题具有相同的最优指派。
,则以C 或 B 为系数矩阵的 指派问题具有相同的最优指派。
例 8 求解指派问题,其系数矩阵为
作业法解:
将第一行元素减去此行中的最小元素 15,同样,第二行元素减去 17,第三行 元素减去 17,最后一行的元素减去 16,得:
再将第 3 列元素各减去 1,得
以![]() 为系数矩阵的指派问题有最优指派
为系数矩阵的指派问题有最优指派
由等价性,它也是C 的最优指派。
python解:
from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[16,15,19,22], [17,21,19,18], [24,22,18,17],[17,19,22,16]])
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:', row_ind) # 开销矩阵对应的行索引
print('col_ind:', col_ind) # 对应行索引的最优指派的列索引
print('cost:', cost[row_ind, col_ind]) # 提取每个行索引的最优指派列索引所在的元素,形成数组
print('cost_sum:', cost[row_ind, col_ind].sum()) # 最小开销
输出结果:
row_ind: [0 1 2 3]
col_ind: [1 0 2 3]
cost: [15 17 18 16]
cost_sum: 66例 9 求解系数矩阵C 的指派问题
python实现:
from scipy.optimize import linear_sum_assignment
import numpy as np
cost = np.array([[12, 7, 9 ,7, 9],
[8, 9, 6, 6, 6],
[7, 17, 12, 14, 12],
[15,14, 6 ,6, 10],
[4,10 ,7 ,10 ,6]])
row_ind, col_ind = linear_sum_assignment(cost)
print('row_ind:', row_ind) # 开销矩阵对应的行索引
print('col_ind:', col_ind) # 对应行索引的最优指派的列索引
print('cost:', cost[row_ind, col_ind]) # 提取每个行索引的最优指派列索引所在的元素,形成数组
print('cost_sum:', cost[row_ind, col_ind].sum()) # 最小开销
输出结果:
row_ind: [0 1 2 3 4]
col_ind: [1 2 0 3 4]
cost: [7 6 7 6 6]
cost_sum: 32
4、对偶理论与灵敏度分析
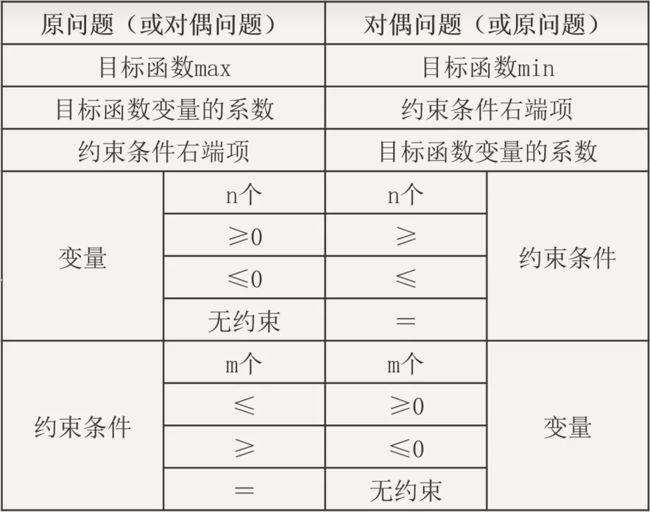
4.1 原始问题和对偶问题
考虑下列一对线性规划模型:
![]() (P)
(P)
和
![]() (D)
(D)
称(P)为原始问题,(D)为它的对偶问题。
不太严谨地说,对偶问题可被看作是原始问题的“行列转置”:
(1) 原始问题中的第 j 列系数与其对偶问题中的第 j 行的系数相同;
(2) 原始目标函数的各个系数行与其对偶问题右侧的各常数列相同;
(3) 原始问题右侧的各常数列与其对偶目标函数的各个系数行相同;
(4) 在这一对问题中,不等式方向和优化方向相反。
考虑线性规划:
![]()
把其中的等式约束变成不等式约束,可得
它的对偶问题是
其中 ![]() 和
和![]() 分别表示对应于约束
分别表示对应于约束 ![]() 和
和 ![]() 的对偶变量组。令
的对偶变量组。令![]() ,则上式又可写成
,则上式又可写成
![]()
原问题和对偶的对偶约束之间的关系:
口诀:
不等号方向相同:Max变量的不等号与min约束条件的不等号方向相同
不等号方向相反:Max约束条件的不等号与min变量的不等号方向相反等号对应无约束:
约束条件的“=”对应变量“无约束”
例题1:
试求下列线性规划的对偶问题。
解:设对应于三个约束的对偶变量分别为y1、y2、y3,则原问题的对偶问题为:
4.2 对偶问题的基本性质
原问题和对偶问题:
(1)对称性
对偶问题的对偶是原问题
(2)弱对偶性
若![]() 是原问题(max)的可行解,
是原问题(max)的可行解,![]() 是对偶问题(min)的可行解,则
是对偶问题(min)的可行解,则![]() ,证:
,证:
max问题:![]() 左乘
左乘![]()
![]()
min问题:![]() 右乘
右乘![]()
![]()
(3)无界性
若原问题(对偶问题)为无界解,则其对偶问题(原问题)无可行解

(4)最优性
设![]() 是原问题的可行解,
是原问题的可行解,![]() 是对偶问题的可行解,当
是对偶问题的可行解,当![]() =府时,
=府时,![]() 是最优解
是最优解
(5)对偶定理
若原问题有最优解,则对偶问题也有最优解,且日标函数值相等
(6)互补松弛性
设![]() 分别是原问题和对偶问题的可行解,
分别是原问题和对偶问题的可行解,![]() 分别是其松弛变量的可行解,则
分别是其松弛变量的可行解,则![]() 是最优解当且仅当
是最优解当且仅当![]() 和
和![]()
例 10 已知线性规划问题:
解 先写出它的对偶问题
添加松弛变量
代入最优解
4.3 灵敏度分析
提出这样两个问题:当这些系数有一个或几个发生变化时,已求得的线性规划问题的最优解会有什么变化;或者这些系数在什么范围内变化时,线性规划问题的最优解或最优基不变。这里我们就不讨论了。
4.4 参数线性规划
参数线性规划是研究![]() 这些参数中某一参数连续变化时,使最优解发生变化 的各临界点的值。即把某一参数作为参变量,而目标函数在某区间内是这参变量的线性 函数,含这参变量的约束条件是线性等式或不等式。因此仍可用单纯形法和对偶单纯形法进行分析参数线性规划问题。
这些参数中某一参数连续变化时,使最优解发生变化 的各临界点的值。即把某一参数作为参变量,而目标函数在某区间内是这参变量的线性 函数,含这参变量的约束条件是线性等式或不等式。因此仍可用单纯形法和对偶单纯形法进行分析参数线性规划问题。
4.4.1 单纯形法:
例题:用单纯形法求解线性规划问题
(1)标准化
(2)使用python编程:
import numpy as np
class Simplex:
def __init__(self) -> None:
self.solutionStatus = 0
def set_param(self, A, b, c, baseInd):
self.A = A
self.m, self.n = self.A.shape
self.b = b
self.c = c
self.baseInd = baseInd
self.nonbaseInd = [i for i in range(self.n) if i not in self.baseInd]
self.B = self.A[:, self.baseInd]
self.N = self.A[:, self.nonbaseInd]
self.B_inv = self.B.I
def main(self):
# 计算非基变量的检验数,基变量检验数为0
reducedCost = [0] * self.n
X_B = None
simplexTable = SimplexTable()
while (self.solutionStatus == 0):
for i in range(self.n):
reducedCost[i] = float(self.c[:, i] - np.dot(self.c[:, self.baseInd], self.A[:, i]))
# p_j已经全部左乘B_inv,因此这里c_B可以直接与更新后的p_j相乘
self.solutionStatus = self.check_solutionStatus(reducedCost)
simplexTable.show(self.A, self.b, self.c, reducedCost, self.baseInd, self.solutionStatus)
if self.solutionStatus == 0:
inVarInd = reducedCost.index(max(reducedCost))
outVarInd = self.get_outVar(inVarInd)
self.baseInd[self.baseInd.index(outVarInd)] = inVarInd
self.nonbaseInd[self.nonbaseInd.index(inVarInd)] = outVarInd
# 得到新基
self.B = self.A[:, self.baseInd]
self.B_inv = self.B.I
self.b = np.dot(self.B_inv, self.b)
X_B = self.b.T.tolist()[0]
self.A[:, inVarInd] = self.A[:, outVarInd]
self.A[:, self.nonbaseInd] = np.dot(self.B_inv, self.A[:, self.nonbaseInd])
else:
break
if self.solutionStatus == 1:
solution = {}
for i in range(self.n):
if i in self.baseInd:
solution[i] = X_B[self.baseInd.index(i)]
if i in self.nonbaseInd:
solution[i] = 0
objctive = float(np.dot(np.dot(self.c[:, self.baseInd], self.B_inv), self.b))
return solution, objctive, self.solutionStatus
else:
solution = None
objctive = None
return solution, objctive, self.solutionStatus
def check_solutionStatus(self, reducedCost):
if all(x < 0 or x == 0 for x in reducedCost):
# 所有检验数<=0
if any(reducedCost[i] == 0 for i in self.nonbaseInd):
# 存在非基变量的检验数为0
return 2 # 无穷多最优解
else:
return 1 # 唯一最优解
else:
if all(all(x < 0 for x in self.A[:, i]) for i in self.nonbaseInd if reducedCost[i] > 0):
return 3 # 无界解
else:
# 选择最大检验数对应的非基变量入基
return 0
def get_outVar(self, inVarInd):
inVarCoef = self.A[:, inVarInd]
ratio = [np.inf] * self.m
for i in range(len(inVarCoef)):
if float(inVarCoef[i, :]) > 0:
ratio[i] = float(self.b[i, :]) / float(inVarCoef[i, :])
outVarInd = self.baseInd[ratio.index(min(ratio))]
return outVarInd
class SimplexTable:
def __init__(self):
# 左端表头格式设置
self.setting_left = '{:^8}'+'{:^8}'+'{:^8}|'
# 右端变量格式设置
self.setting_var = '{:^8}|'
# 求解状态格式设置
self.setting_status = '{:^24}|'+'{:^44}|'
def show(self,A,b,c,reducedCost,baseInd,solutionStatus):
var_num = A.shape[1]
# 打印系数行
c_j_list = c.flatten().tolist()[0]
print('='*80)
print(self.setting_left.format('','c_j',''),end = '')
for i in c_j_list:
print(self.setting_var.format(i),end = '')
print()
# 打印变量行
print(self.setting_left.format('c_B','x_B','b'),end = '')
for i in range(var_num):
print(self.setting_var.format('x'+str(i)),end = '')
print()
# 打印变量与矩阵
for i in range(len(baseInd)):
varInd = baseInd[i]
varCeof = round(float(c[:,varInd]),2)
varValue = round(float(b[i,:]),2)
row = A[i,:].flatten().tolist()[0]
print(self.setting_left.format(str(varCeof),'x'+str(varInd),str(varValue)),end='')
for i in range(var_num):
print(self.setting_var.format(round(row[i],2)),end = '')
print()
# 打印检验数
print(self.setting_left.format('','c_j-z_j',''),end='')
for i in reducedCost:
print(self.setting_var.format(round(i,2)),end = '')
print()
# 显示求解状态
if solutionStatus == 0:
print(self.setting_status.format('status','...Iteration continues...'))
if solutionStatus == 1:
print(self.setting_status.format('status','Unique Optimal Solution'))
B = A[:,baseInd]
B_inv = B.I
objctive = float(np.dot(np.dot(c[:, baseInd], B_inv), b))
print(self.setting_status.format('objctive', round(objctive,2)))
solution = [0]*var_num
X_B = b.T.tolist()[0]
for i in range(var_num):
if i in baseInd:
solution[i] = X_B[baseInd.index(i)]
print(self.setting_left.format('', 'solution', ''), end='')
for i in solution:
print(self.setting_var.format(round(i, 2)), end='')
print()
if solutionStatus == 2:
print(self.setting_status.format('status','Multiple Optimal Solutions'))
B = A[:, baseInd]
B_inv = B.I
objctive = float(np.dot(np.dot(c[:, baseInd], B_inv), b))
print(self.setting_status.format('objctive', round(objctive, 2)))
if solutionStatus == 3:
print(self.setting_status.format('status','Unboundedness'))
'''=============================================================================='''
A = np.matrix([[0,5,1,0,0],
[6,2,0,1,0],
[1,1,0,0,1]], dtype=np.float64)
# 必须设置精度,否则在替换矩阵列时会被自动圆整
b = np.matrix([[15], [24], [5]], dtype=np.float64)
c = np.matrix([2,1,0,0,0], dtype=np.float64)
baseInd = [2,3,4]
s=Simplex()
s.set_param( A, b, c, baseInd)
s.main()以此形式进行列表求解,满足单纯形法的基本条件,具体如下:
================================================================================
c_j | 2.0 | 1.0 | 0.0 | 0.0 | 0.0 |
c_B x_B b | x0 | x1 | x2 | x3 | x4 |
0.0 x2 15.0 | 0.0 | 5.0 | 1.0 | 0.0 | 0.0 |
0.0 x3 24.0 | 6.0 | 2.0 | 0.0 | 1.0 | 0.0 |
0.0 x4 5.0 | 1.0 | 1.0 | 0.0 | 0.0 | 1.0 |
c_j-z_j | 2.0 | 1.0 | 0.0 | 0.0 | 0.0 |
status | ...Iteration continues... |
================================================================================
c_j | 2.0 | 1.0 | 0.0 | 0.0 | 0.0 |
c_B x_B b | x0 | x1 | x2 | x3 | x4 |
0.0 x2 15.0 | 0.0 | 5.0 | 1.0 | 0.0 | 0.0 |
2.0 x0 4.0 | 1.0 | 0.33 | 0.0 | 0.17 | 0.0 |
0.0 x4 1.0 | 0.0 | 0.67 | 0.0 | -0.17 | 1.0 |
c_j-z_j | 0.0 | 0.33 | 0.0 | -0.33 | 0.0 |
status | ...Iteration continues... |
================================================================================
c_j | 2.0 | 1.0 | 0.0 | 0.0 | 0.0 |
c_B x_B b | x0 | x1 | x2 | x3 | x4 |
0.0 x2 7.5 | 0.0 | 0.0 | 1.0 | 1.25 | -7.5 |
2.0 x0 3.5 | 1.0 | 0.0 | 0.0 | 0.25 | -0.5 |
1.0 x1 1.5 | 0.0 | 1.0 | 0.0 | -0.25 | 1.5 |
c_j-z_j | 0.0 | 0.0 | 0.0 | -0.25 | -0.5 |
status | Unique Optimal Solution |
objctive | 8.5 |
solution | 3.5 | 1.5 | 7.5 | 0 | 0 |最优解:![]()
最优值:![]()
单纯形法的进一步讨论:
1.人工变量法(大M法)
一些线性规划问题在化为标准形后约束条件系数矩阵不存在单位矩阵,就需要在约束条件中添加人工变量构造一个新的线性规划问题。将人工变量在目标函数中的系数取任意大的负数,在求解过程中可以防止人工变量出现在最优解中。若在最终单纯形表中所有检验数都小于等于零,但基变量中仍存在不为零的人工变量,则问题无解。下面,给出人工变量法的计算步骤。
2.两阶段法
用大M法处理人工变量,在用电子计算机求解时,对M只能在计算机内输入一个机器最大字长的数字。如果线性规划问题中的参数值与这个代表M的数比较接近,或远远小于这个数字,由于计算机计算时取值上的误差,有可能使计算结果发生错误。
为了克服这个困难,可以对添加人工变量后的线性规划问题分两个阶段来计算,称两阶段法。
进一步了解:运筹说 第16期 | 线性规划硬核知识点梳理—单纯形法 - 知乎
4.4.2 对偶单纯形法:
例题:用对偶单纯形法求解LP:
(1)标准化:
将两个等式约束两边分别乘以-1,得
(2)使用python编程:
import re
import pandas as pd
from fractions import Fraction
# data = pd.read_csv("data2.csv", header=0, index_col=0)
# data=pd.DataFrame({"x1":[-2,-2,-1,-9],"x2":[-2,-3,-1,-12],"x3":[-1,-1,-5,-15],"x4":[1,0,0,0],"x5":[0,1,0,0],"x6":[0,0,1,0],"b":[-10,-12,-14,0]},index = ['x4', 'x5', 'x6',"sigma"])
data=pd.DataFrame({"x1":[-1,-2,-2],"x2":[-2,1,-3],"x3":[-1,-3,-4],"x4":[1,0,0],"x5":[0,1,0],"b":[-3,-4,0]},index = ['x4', 'x5' ,"sigma"])
print("=======原始表=======")
print(data)
def do_it(data):
in_base_index = data.loc["sigma", :][data.loc['sigma', :] < 0].index
rec = {}
res_val = []
for i in in_base_index:
out_base_index = data.loc[:, i][data.loc[:, i] < 0].index.drop("sigma")
for j in out_base_index:
res = Fraction(data.loc["sigma", i], data.loc[j, i])
res_val.append(res)
rec[str(j) + "," + str(i)] = res
def get_key(dic, value):
return [k for k, v in dic.items() if v == value]
s = get_key(rec, min(res_val))
s = re.split(r"\,", s[0])
# 这里是将本身变成1
param1 = Fraction(1, data.loc[s[0], s[1]])
data.loc[s[0], :] = data.loc[s[0], :] * param1
# 将其他变为0
for row in data.index.drop(s[0]):
target = data.loc[row, s[1]]
param2 = Fraction(-target, 1)
data.loc[row, :] = data.loc[s[0], :] * param2 + data.loc[row, :]
data = data.rename(index={s[0]: s[1]})
print("================================")
print(data)
if (data["b"].drop("sigma") < 0).any():
print("需要继续迭代!")
do_it(data)
else:
print("迭代结束!")
return data
# 如何b中的任何一个数小于零,都需要进一步操作
if (data["b"].drop("sigma") < 0).any():
print("需要继续迭代!")
do_it(data)
else:
print("迭代结束!")以此形式进行列表求解,满足对偶单纯形法的基本条件,具体如下:
=======原始表=======
x1 x2 x3 x4 x5 b
x4 -1 -2 -1 1 0 -3
x5 -2 1 -3 0 1 -4
sigma -2 -3 -4 0 0 0
需要继续迭代!
================================
x1 x2 x3 x4 x5 b
x4 0 -5/2 1/2 1 -1/2 -1
x1 1 -1/2 3/2 0 -1/2 2
sigma 0 -4 -1 0 -1 4
需要继续迭代!
================================
x1 x2 x3 x4 x5 b
x2 0 1 -1/5 -2/5 1/5 2/5
x1 1 0 7/5 -1/5 -2/5 11/5
sigma 0 0 -9/5 -8/5 -1/5 28/5
迭代结束!最优解:![]()
最优值:![]()


![C=\left[\begin{array}{llll} 16 & 15 & 19 & 22 \\ 17 & 21 & 19 & 18 \\ 24 & 22 & 18 & 17 \\ 17 & 19 & 22 & 16 \end{array}\right]](http://img.e-com-net.com/image/info8/8b0bc1431c0f427093f8ef8e46dc9866.gif)
![B_{1}=\left[\begin{array}{llll} 1 & 0 & 4 & 7 \\ 0 & 4 & 2 & 1 \\ 7 & 5 & 1 & 0 \\ 1 & 3 & 6 & 0 \end{array}\right]](http://img.e-com-net.com/image/info8/b8722b08a50a4e9db46cb36a889ccc09.gif)
![B_{2}=\left[\begin{array}{cccc} 1 & 0^{*} & 3 & 7 \\ 0^{*} & 4 & 1 & 1 \\ 7 & 5 & 0^{*} & 0 \\ 1 & 3 & 5 & 0^{*} \end{array}\right]](http://img.e-com-net.com/image/info8/43296d1a5fda422cbaf0b2eb99a290d9.gif)