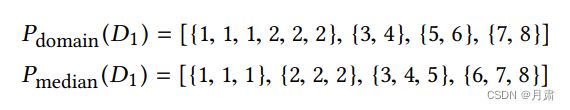A Robust Partitioning Scheme for Ad-Hoc Query Workloads论文阅读
目录
- A Robust Partitioning Scheme for Ad-Hoc Query Workloads
- 主要内容
- 分区建立与变换方法
-
- 分区建立
- 分区变换
-
- 交换
- 属性上推
- 旋转
- 算法部分
A Robust Partitioning Scheme for Ad-Hoc Query Workloads
主要内容
对于数据分区而言,不能过多地加入个人主观判断,即认为历史(或已读取)的查询具有代表性。文章举出一个物联网公司的例子,在公司数据库已获得80%的的查询下,剩余20%的查询里仍存在57%的新查询,因此静态查询负载的分析不一定好用。文章认为动态查询分析较静态而言具有更好的鲁棒性。如果单单是动态分析一个属性,那么对于查询效率而言,一开始可能还不如遍历所有的块来的快,但是一定的查询量积累下来之后模型的效果就会非常好;但是,一旦查询改变属性,那么分区查询效率将又回到不如遍历的状态,整体将如图所示:
因此需要一次性进行多属性分析。
分区建立与变换方法
分区建立
分区建立的索引树是异构的(这点和Robust data partitioning for ad-hoc query processing相似)。
首先要进行初始化分区。举个例子,现在有数据 D 1 = { 1 , 1 , 1 , 2 , 2 , 2 , 3 , 4 , 5 , 6 , 7 , 8 } D_{1}=\{1, 1, 1, 2, 2, 2, 3, 4, 5, 6, 7, 8\} D1={1,1,1,2,2,2,3,4,5,6,7,8}文章给出两个假设,即按照域范围划分和按照中位数划分出4个分区:
可以看到按照域范围划分的结果是很不平衡的(这个例子多少有点极端了),而按照中位数是很平衡的。为了提高分区效率,选择了尽量平衡的中位数分区法,以此来完成初始化分区。(分区方式确实可以改进,可以按照具体的负载制定具体的划分标准,当然文中这并不是重点。)
初始化算法如图,输入数据集规模,最大分区大小,属性分配比例,元组数据;
计算叶节点桶的数量,从而获得树的最大深度maxDepth,将根节点(所有数据),树的深度,初始数据加入队中;
当队非空,重复如下操作:
- 第一个数据出队,获取节点,节点深度,节点数据;
- 当节点深度大于0时,执行以下操作:
-
- 使用leastAllocated(allocation)获取当前节点的属性;
- 使用findMedian()获取当前属性对应数据的中位数;
- 分配左右子节点,压入队中;
- allocation对应的属性减去 2.0 2 m a x D e p t h − d e p t h \frac{2.0}{2^{maxDepth-depth}} 2maxDepth−depth2.0;
- 节点深度depth减1;
- 若节点深度不大于0,则创建新桶作为节点;
分区变换
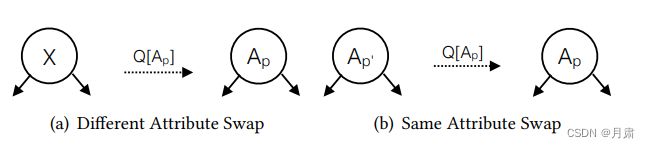
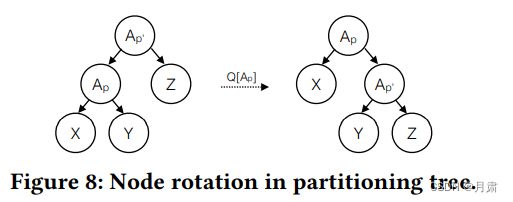
设定A为表中某属性, A p A_{p} Ap表示A 根据只改变查询到的数据的原则,我们尽量只交换低层节点,因为这样改变的数据分区较少。当交换的是不同属性,如 B p ′ B_{p'} Bp′时,交换后节点对应的两个子节点都要重新改写;当交换的是同一个属性时,如 A p ′ A_{p'} Ap′,假设p=5,p’=10,那么就将交换前左子节点的[5, 10]部分划入右子节点可以了。 将频繁的属性尽量推到靠近根节点的位置,但是前提是被推至的节点的子节点恰好包含incoming predicate。 每次交换之前都会检查可不可以属性上推,因为属性交换高层节点的成本很高;另一个好处是属性上推的作用是双向的,休眠节点的属性被动下推,这样可以提升查询速率。 旋转转换重新排列同一属性上的两个谓词,以便更重要的(最近访问或频繁出现在查询序列中)谓词在分区树中出现在更高的位置。 算法的实现简单暴力。我们要寻找当前的最佳分区,当前的最佳分区是由左右子树构成的,因此我需要寻找左右子树的当前最佳分区,这时便产生了递归调用函数。 第一阶段,当我找到叶子节点时,什么都不做,仅仅返回;当我返回到上一节点时,如果该节点的子节点全部被访问了的话,计算当前查询cost,将节点替换为查询所涉及的属性进行划分,再次计算cost,根据两个cost的大小决定是否更新树的结构; 第二阶段,当某一节点经过第一阶段后的两个子节点均变为同一个属性划分时,将子节点属性上提,父节点属性下推; 第三阶段,检测当前节点是否为查询谓词,若是的话比较旋转之后的cost,以此来判断是非应该旋转。 当面对同一属性的不同谓词划分时,算法如图 考虑一个具有两个谓词Ap和Ap2的简单查询,其划分方法是考虑选择一组要由Ap替换的访问非终端节点,然后对于每个这样的选择,从剩余节点中选择要由Ap2替换的节点。其余的评价标准类似。交换
属性上推
旋转
算法部分