GAN论文阅读笔记
Generative Adversarial Nets
论文链接
摘要
我们提出了一个通过对抗过程来估计生成模型的新框架,在这个框架中,我们同时训练两个模型:捕获数据分布的生成模型G,以及估计样本来自训练数据的概率的判别模型D。G训练过程是为了使D犯错误的可能性最大化。这个框架对应于一个极大化极小化的双人博弈。在任意函数G和D的空间中存在一个唯一的解,其中G恢复训练数据分布,D处处都等于1/2。在G和D由多层感知器定义的情况下,整个系统可以用反向传播进行训练。在样本的训练和生成过程中,不需要任何马尔可夫链或展开的近似推理网络。通过对生成的样本进行定性和定量评估,实验证明了该框架的潜力。
一、引言
深度学习的任务是发现丰富的层次模型,该模型能够表示人工智能应用中遇到的各种数据的概率分布,如自然图像、包含语音的音频波形和自然语言语料库中的符号。到目前为止最成功的的模型之一是判别式模型,通常它们将高维丰富的感知机输入映射到类标签上,这些显著的成功主要是基于反向传播算法和dropout算法,特别是具有良好梯度的分段线性单元。因为在极大似然估计和相关策略中产生的许多棘手的概率计算,并且难以在生成环境中利用分段线性单元的好处,深度生成模型的影响很小,我们提出了一种新的生成模型估计程序,来分布处理这些难题。
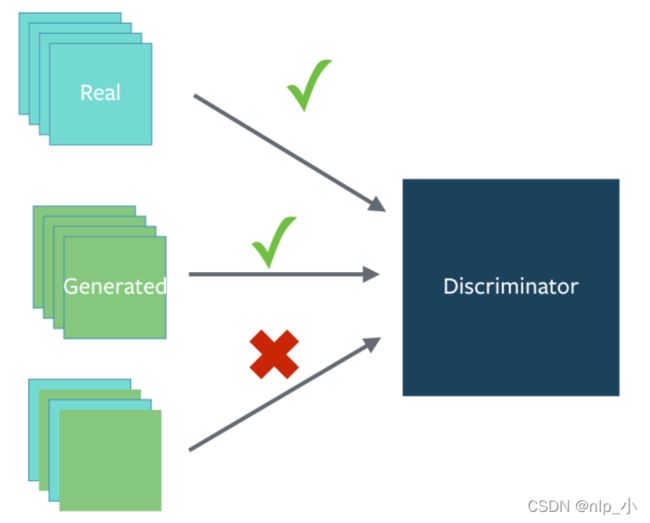
在提到的对抗网络框架中,生成模型与一个对手相对抗:判别模型,它学会判断样本是来自模型分布还是来自数据分布。生成模型可以被认为类似于一组伪造者,他们试图制造假币并在不被发现的情况下使用它,而判别模型则类似于警察,他们试图发现假币。在这个游戏中的竞争驱使两队改进他们的方法,直到假货与正品无法区分。
该框架可以为多种模型和优化算法生成特定的训练算法。在本文中,我们探讨了生成模型通过随机噪声输入到多层感知机来生成样本的特殊情况,而判别模型也是一个多层感知机。我们把这种特殊情况称为对抗网。在这种情况下,我们可以只使用非常成功的反向传播算法和dropout算法来训练这两个模型,而只使用前向传播来训练生成模型生成的样本,不需要近似推理或马尔可夫链。
二、相关工作
具有隐变量的有向图模型可以由含隐变量的无向图模型代替,如受限玻尔兹曼机(RBMs)、深度玻尔兹曼机(DBMs)及其众多变体。这些模型之间的相互作用被表示为非归一化的势函数的乘积,在通过对随机变量的所有状态进行全局整合来进行归一化。这个数量(配分函数)及其梯度的估算是很棘手的,尽管它们可以用马尔可夫链和蒙特卡罗(MCMC)方法来估计,同时依靠MCMC学习算法的混合也会带来了一个严重问题。
深度信念网络(DBNs)是包含一个无向层和若干个有向层的混合模型。当使用一个快速近似的分层训练准则时,DBNs会引发无向模型和有向模型相关计算难题。
不利用似然函数的估计或约数的选择准则已经被提出来了,如分数匹配和噪声对比估计(NCE)。这两种方法都需要知道先验概率密度知识用来分析指定一个规范化的常量。请注意,在许多具有多层隐变量的有趣生成模型中(如DBNs和DBMs),甚至不可能导出可处理的非标准化概率密度。一些模型,如去噪自动编码器[30]和收缩自动编码器,其学习规则与应用于RBM的分数匹配非常相似。在NCE中,就像在这项工作中一样,一个判别训练标准被用来拟合一个生成模型。然而,生成模型本身不是用来拟合单独的判别模型,而是用来从固定噪声分布的样本中判别生成的数据。因为NCE使用的是固定的噪声分布,当模型在观察变量的一小部分上学习到一个近似正确的分布后,学习速度会显著降低。
最后,有些技术没有明确地定义一个概率分布,而是训练生成器从期望的分布中拟合出样本。这种方法的优点是,这样的机器可以设计成通过反向传播进行训练。最近在这一领域的突出工作包括生成随机网络(GSN)框架,它扩展了广义降噪自编码器:两者都可以被视为定义了一个参数化的马尔可夫链,也就是说,一个可以通过执行生成马尔可夫链的一个步骤来学习机器参数的算法。与GSNs相比,对抗网框架不需要马尔可夫链进行采样。由于对抗网络在生成过程中不需要反馈循环,它们能够更好地利用分段线性单元,这提高了反向传播的性能,但在使用反馈循环时存在无界激活的问题。最近通过反向传播来训练生成机的例子包括最近关于变分贝叶斯自编码器和随机反向传播的研究。
三、对抗网络
当模型是多层感知机时,对抗模型框架是最直接应用的。为了学习生成器关于数据 x x x上的分布 p g p_g pg,我们定义输入噪声的先验变量 p z ( z ) p_z(z) pz(z),然后使用 G ( z ; θ g ) G(z;\theta_g) G(z;θg)来表示数据空间的映射。这里G是一个由含参数 θ g \theta_g θg的多层感知机表示的可微函数。我们再定义了一个多层感知机 D ( x ; θ d ) D(x;\theta_d) D(x;θd)用来输出一个单独的标量。其中 D ( x ) D(x) D(x)表示 x x x来自于真实数据分布而不是 p g p_g pg的概率,我们训练 D D D来最大化分配正确标签给不管是来自训练样本还是 G G G生成的样本的概率,我们同时训练 G G G来最小化 l o g ( 1 − D ( G ( z ) ) ) log(1-D(G(z))) log(1−D(G(z)))。换句话说,D和G的训练是关于值函数V(G,D)的极小化极大化的二人博弈问题:
m i n G m a x D V ( D , G ) = E x ∽ p d a t a ( x ) [ l o g D ( x ) ] + E z ∽ p z ( z ) [ l o g ( 1 − D ( G ( z ) ) ) ] . ( 1 ) {min\atop G} \space {max\atop D}\space V(D,G)=E_{x\backsim p_{data} (x)}[logD(x)]+E_{z\backsim p_z(z)}[log(1-D(G(z)))].\space \space\space\space\space\space\space\space\space\space\space\space\space\space(1) Gmin Dmax V(D,G)=Ex∽pdata(x)[logD(x)]+Ez∽pz(z)[log(1−D(G(z)))]. (1)
在下一节中,我们提出了对抗网络的理论分析,基本上表明基于训练准则可以恢复数据生成分布,因为 G G G和 D D D被给予足够的容量,即在非参数极限。如图1展示了该方法的一个非正式却更加直观的解释。实际上,我们必须使用迭代数值方法来实现这个过程。在训练的内部循环中优化 D D D到完成的计算是禁止的,并且有限的数据集将导致过拟合。相反,我们在优化 D D D的 k k k个步骤和优化 G G G的一个步骤之间交替。只要 G G G变化足够慢,可以保证 D D D保持在其最佳解附近。该过程如算法1所示。
实际上,方程1可能无法为 G G G提供足够的梯度来学习。训练初期,因为它们与训练数据明显不同,当 G G G的生成效果很差时, D D D会以高置信度来辨别出生成样本。因此, l o g ( 1 − D ( G ( z ) ) ) log(1−D(G(z))) log(1−D(G(z)))饱和,并趋向于0,难以训练生成器G,此时,我们选择最大化 l o g D ( G ( z ) ) logD(G(z)) logD(G(z))而不是最小化$log(1−D(G(z))) 来 训 练 来训练 来训练G , 该 目 标 函 数 使 ,该目标函数使 ,该目标函数使G 和 和 和D$的动力学稳定点相同,并且在训练初期,该目标函数可以提供更强大的梯度。
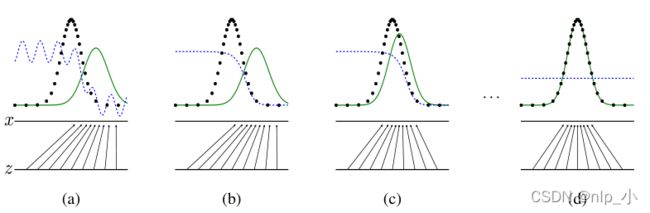
图1:生成对抗网络是通过同时更新判别器分布( D D D,蓝色虚线)来训练的,这样它就可以区分来真实数据分布(黑色,点划线)的样本 p x p_x px和来自生成器的分布(绿色,实线)的样本 p G p_G pG。下方的水平线是x的定义域的一部分,向上的箭头展示了噪声 z z z是如何通过 x = G ( z ) x=G(z) x=G(z)映射的。 G G G在高密度区域收缩,在低密度区域膨胀。(a)考虑到一个接近收敛的对抗性组合: p g p_g pg和 p d a t a p_{data} pdata相似, D D D是一个部分准确的分类器。(b)在算法的内部循环中训练 D D D来辨别出数据中的样本, D D D收敛于 D ∗ ( x ) = p d a t a ( x ) / ( p d a t a ( x ) + p g ( x ) ) D^*(x)=p_{data}(x) / (p_{data}(x) + p_g(x)) D∗(x)=pdata(x)/(pdata(x)+pg(x))。©在G更新一次之后, D D D的梯度引导着 G ( z ) G(z) G(z)更可能地被分类为数据中样本。(d)随着训练的进行,生成器生成的数据分布逐渐接近原始数据,然后判别器无能为力,给出 D ( x ) = 0.5 D(x)=0.5 D(x)=0.5的概率,此时 p g = p d a t a p_g=p_{data} pg=pdata。
四、理论结果
生成器 G G G隐式地定义了一个概率分布 p g p_g pg,即当 z ∽ p z z\backsim p_z z∽pz时,得到的样本 G ( z ) G(z) G(z)的概率分布,因此,如果有足够的容量和训练时间,我们希望算法1收敛到一个好的 p d a t a p_{data} pdata估计。本节的结果是在非参数设置中完成的,例如,我们通过研究概率密度函数空间中的收敛来表示一个具有无限容量的模型。
我们将在4.1节中展示这个极大化极小化游戏有一个全局最优解 p g = p d a t a p_g=p_{data} pg=pdata。我们将在4.2节中展示,算法1优化了方程(1),从而得到了预期的结果。

4.1 全局最优** p g = p d a t a p_g=p_{data} pg=pdata**
我们首先考虑在给定任一生成器 G G G的情况下,辨别器 D D D的最优。
-
Proposition 1 在给定G的情况下,辨别器D的最优是
D G ∗ ( x ) = p d a t a ( x ) p d a t a ( x ) + p g ( x ) ( 2 ) D^*_G(x)={p_{data}(x) \over p_{data}(x)+p_g(x)} \space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space(2) DG∗(x)=pdata(x)+pg(x)pdata(x) (2)Proof 对于任意生成器 G G G,鉴别器 D D D的训练准则是使量值 V ( G , D ) V (G, D) V(G,D)最大化。
V ( G , D ) = ∫ x p d a t a ( x ) l o g ( D ( x ) ) d x + ∫ z p z ( z ) l o g ( 1 − D ( g ( z ) ) ) d z = ∫ x p d a t a ( x ) l o g ( D ( x ) ) + p g ( x ) l o g ( 1 − D ( x ) ) d x ( 3 ) V(G,D)=\int_xp_{data}(x)log(D(x))dx+\int_zp_z(z)log(1-D(g(z)))dz \\ = \int_xp_{data}(x)log(D(x))+p_g(x)log(1-D(x))dx \space\space\space\space\space\space\space\space\space(3) V(G,D)=∫xpdata(x)log(D(x))dx+∫zpz(z)log(1−D(g(z)))dz=∫xpdata(x)log(D(x))+pg(x)log(1−D(x))dx (3)对于任意 ( a , b ) ∈ R 2 ∖ { 0 , 0 } (a, b)\in \Reals^2 \setminus \{0,0\} (a,b)∈R2∖{0,0},函数KaTeX parse error: Undefined control sequence: \ce at position 1: \̲c̲e̲{y -> a\space l…在[0,1]内 a ∖ ( a + b ) a \setminus (a+b) a∖(a+b)处取最大值,辨别器不需要在 S u p p ( p d a t a ) ∪ S u p p ( p g ) Supp(p_{data})\cup Supp(p_g) Supp(pdata)∪Supp(pg)的外部进行定义。
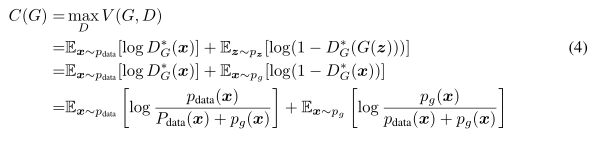
-
Theorem 1 当且仅当 p g = p d a t a p_g=p_{data} pg=pdata时,得到虚拟训练准则 C ( G ) C(G) C(G)取全局最小值。此时,C(G)为−log 4。
Proof 当 p g = p d a t a p_g=p_{data} pg=pdata时, D G ∗ ( x ) = 0.5 D^*_G(x) = 0.5 DG∗(x)=0.5,此时 C ( G ) = l o g 0.5 + l o g 0.5 = − l o g 4 C(G) = log0.5+log0.5 = -log4 C(G)=log0.5+log0.5=−log4
简化表达式 C ( G ) = V ( D G ∗ , G ) C(G)=V(D^*_G,G) C(G)=V(DG∗,G),可以得到如下式子:
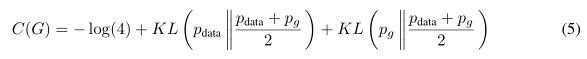
KL散度 KL(P||Q)用来衡量P,Q这两个概率分布差异
K L ( P ∣ ∣ Q ) = ∫ x P ( x ) ( l o g P ( x ) − l o g Q ( x ) ) d x KL(P||Q)=\int_{x}P(x)(log \space P(x)-log\space Q(x))dx KL(P∣∣Q)=∫xP(x)(log P(x)−log Q(x))dxKL是Kullback-Leibler的分流。在前面的表达式中,我们认识到模型分布和数据生成过程之间的Jensen - Shannon散度
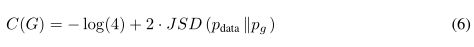
JSD 表示JS散度,是KL散度的一种变形,也是用来表示两个分布之间的差异,JS散度与KL散度不同的是,JS散度是对称的
J S D ( P ∣ ∣ Q ) = 1 2 K L ( P ∣ ∣ M ) + 1 2 K L ( Q ∣ ∣ M ) , M = 1 2 ( P + Q ) JSD(P||Q)=\frac{1}{2}KL(P||M)+\frac{1}{2}KL(Q||M),M=\frac{1}{2}(P+Q) JSD(P∣∣Q)=21KL(P∣∣M)+21KL(Q∣∣M),M=21(P+Q)由于两个分布之间的Jensen-Shannon散度只有在它们相等时才总是非负且为零,我们已经证明了 C ∗ = − l o g ( 4 ) C^∗=−log(4) C∗=−log(4)是 C ( G ) C(G) C(G)的全局最小值,并且唯一的解为 p g = p d a t a p_g=p_{data} pg=pdata,即生成模型完美地复制了数据生成过程。
4.2 算法1的收敛性
- Proposition 2如果 G G G和 D D D有足够的容量,在算法1的每一步中,都允许辨别器达到在给定 G G G的情况下的最优值,并更新 p g p_g pg来改进准则 E x ∽ p d a t a [ l o g D G ∗ ( x ) ] + E x ∽ p g [ l o g ( 1 − D G ∗ ( x ) ) ] E_{x\backsim p_{data}}[log\space D^*_G(x)]+E_{x\backsim p_g}[log(1-D^*_G(x))] Ex∽pdata[log DG∗(x)]+Ex∽pg[log(1−DG∗(x))],最后 p g p_g pg收敛于 p d a t a p_{data} pdata
Proof 将 V ( G , D ) = U ( p g , D ) V(G,D)=U(p_g,D) V(G,D)=U(pg,D)作为上述准则中关于 p g p_g pg的函数,注意到 U ( p g , D ) U(p_g,D) U(pg,D)是凸的,凸函数的上界的次导数包括该函数在达到最大值点处的倒数,换句话说,如果 f ( x ) = s u p α ∈ A f α ( x ) f(x)=sup_{\alpha \in A}f_{\alpha}(x) f(x)=supα∈Afα(x)对于每一个 α \alpha α函数关于 x x x都是凸的, ∂ f β ( x ) ∈ ∂ f ∂f_β(x)∈∂f ∂fβ(x)∈∂f 如果 β = a r g s u p α ∈ A f α ( x ) β= arg sup_{α∈A}f_α(x) β=argsupα∈Afα(x)。这相当于在给定相应 G G G的情况下为 p g p_g pg计算一个最优的梯度下降更新。 s u p D U ( p g , D ) sup_DU(p_g, D) supDU(pg,D)关于 p g p_g pg是凸的,具有Thm1中证明的唯一全局最优值,因此,只要对 p g p_g pg进行足够小的更新, p g p_g pg收敛于 p x p_x px,从而得出证明
事实上,对抗网通过函数 G ( z ; θ g ) G (z;θ_g) G(z;θg)表示一个有限族的 p g p_g pg分布,我们优化 θ g θ_g θg而不是 p g p_g pg本身。使用多层感知机来定义 G G G,在参数空间中引入多个临界点。然而,多层感知机在实践中的优异性能表明,尽管缺乏理论保障,但它们是一个可以使用的合理模型。
五、优缺点
与以前的建模框架相比,这个新框架既有优点也有缺点。缺点主要是 p g ( x ) p_g(x) pg(x)没有显式的表示,训练时 D D D必须与 G G G很好地同步(特别是 G G G不能训练过多而不更新 D D D,为了避免“Helvetica场景”,即 G G G折叠太多的 z z z值到相同的 x x x值,从而有足够的多样性来建模 p d a t a p_{data} pdata),就像玻尔兹曼机器的负链必须在学习步骤之间保持最新。其优点是不需要马尔可夫链,只使用反向传播来获取梯度,在学习过程中不需要推理,可以将各种各样的函数合并到模型中。表2总结了生成式对抗网与其他生成式建模方法的比较。
上述优点主要是计算方面的。对抗模型也可以从生成器网络中获得一些统计优势,而不是直接用数据示例来更新,而只是用通过鉴别器的梯度来更新。这意味着输入的组件不会直接复制到生成器的参数中。对抗网络的另一个优点是,它们可以表示非常尖锐、甚至退化的分布,而基于马尔可夫链的方法要求分布有点模糊,以便链能够在模式之间混合。
六、总结和未来工作
这个框架允许许多简单的扩展:
- 条件生成模型 p ( x ∣ c ) p(x|c) p(x∣c)可以通过在 G G G和 D D D中同时添加 c c c作为输入而得到
- 学习近似推理可以由训练辅助网络预测z给x。这类似于和生物钟的推理网络训练算法但推理网络的优势可能被训练为一个固定的完成训练的生成器网络。
- 我们可以对所有条件$p(x_S|x_{$}) 进 行 近 似 建 模 , 其 中 进行近似建模,其中 进行近似建模,其中S 是 是 是x$指标的一个子集,方法是训练一组共享参数的条件模型。本质上,我们可以使用对抗网来实现确定性MP-DBM的随机扩展。
- 半监督学习:来自鉴别器或推理网的特征可以提高分类器的性能,当有限制的标记数据可用。
- 效率提高:训练可以通过划分更好的方法来大大加速协调G和D,或者在训练过程中确定样本z的更好分布。
本文论证了对抗建模框架的可行性,表明这些研究方向可能会被证明是有用的。
GAN理解
优质经验贴1
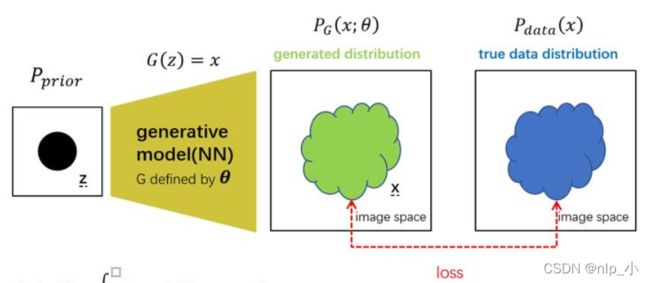
GAN的本质是在做一个极大似然估计的任务,即使生成器概率分布 P G ( x ; θ ) P_G(x; \theta) PG(x;θ)尽可能的拟合真实数据分布 P d a t a ( x ) P_{data}(x) Pdata(x),但由于真实数据难以用确定的分布进行表示,于是就找到一个分布来近似真实数据分布,一般的分布模型如:高斯分布,其拟合数据的能力较弱,目前拟合能力强劲的神经网络快速发展,于是就采用神经网络模型(也就是GAN中的生成器)来得到 P G ( x ; θ ) P_G(x;\theta) PG(x;θ)
其中 P p r i o r P_{prior} Pprior是先验分布, I [ ] I_{[\space]} I[ ]其括号中为真时取1,假时取0。 z z z是从 P p r i o r P_{prior} Pprior中取样的数据,生成其 G ( ) G() G()将 z z z作为输入,生成 x x x从而来构建分布 P G ( x ; θ ) P_G{(x;\theta)} PG(x;θ),通过构建适当的loss函数来计算出分布 P d a t a ( x ) P_{data}(x) Pdata(x)和 P G ( x ; θ ) P_G(x;\theta) PG(x;θ)的差异,来不断优化神经网络G的参数,最后使得 P G ( x ; θ ) P_G(x;\theta) PG(x;θ)越来越接近真实数据分布,最后达到能够拟合真实数据分布。
使用极大似然估计来计算出 P G ( x ; θ ) P_G(x;\theta) PG(x;θ)的过程太复杂,为此引入了判别器D,用来评估生成器G生成数据的分布 P G ( x ; θ P_G(x;\theta PG(x;θ)与真实数据的分布 P d a t a ( x ) P_{data}(x) Pdata(x)之间的差异
其GAN的目标是:得到使 m a x D V ( D , G ) \space {max\atop D}\space V(D,G) Dmax V(D,G)最小的生成器 G G G
V ( D , G ) = E x ∽ p d a t a ( x ) [ l o g D ( x ) ] + E z ∽ p z ( z ) [ l o g ( 1 − D ( G ( z ) ) ) ] . V(D,G)=E_{x\backsim p_{data} (x)}[logD(x)]+E_{z\backsim p_z(z)}[log(1-D(G(z)))]. V(D,G)=Ex∽pdata(x)[logD(x)]+Ez∽pz(z)[log(1−D(G(z)))].
- **在给定G的情况下,**** m a x D V ( D , G ) \space {max\atop D}\space V(D,G) Dmax V(D,G)的大小衡量着 P d a t a ( x ) P_{data}(x) Pdata(x)和 P G ( x ; θ ) P_G(x;\theta) PG(x;θ)**差异大小
证明:
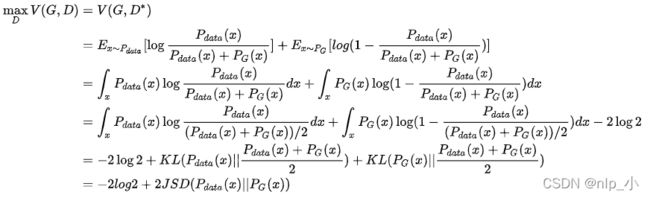
GAN的训练过程:
GAN在同一轮梯度反向传递的过程中,可以细分为两步,首先训练判别器D,然后再训练生成器G
判别器D的训练需要上一轮梯度反向传递中生成器G的输出值作为输入,并非等判别器D完全训练好后,才开始训练G,在训练生成器G的时候,其中判别器D的参数是不可训练的


GAN实战
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import glob
import os
(train_images, train_labels), (_, _) = tf.keras.datasets.mnist.load_data()
train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
train_images = (train_images - 127.5)/127.5
BATCH_SIZE = 256
BUFFER_SIZE = 60000
datasets = tf.data_Dataset.from_tensor_slices(train_images)
datasets = tf.shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
def generator_model():
model = keras.Sequential()
model.add(layers.Dense(256, input_shape=(100, ), use_bias=False))
model.add(layers.BatchNormalization())
model.add(layers.LeakReLU())
model.add(layers.Dense(512, use_bias=False))
model.add(layers.BatchNormalization())
model.add(layers.LeakReLU())
model.add(layers.Dense(28*28*1, use_bias=False))
model.add(layers.BatchNormalization())
model.add(layers.LeakReLU())
model.add(layers.Reshape((28, 28, 1)))
return model
def discriminator_model():
model = keras.Sequential()
model.add(layers.Flatten())
model.add(layers.Dense(512, use_bias=False))
model.add(layers.BatchNormalization())
model.add(layers.LeakReLU())
model.add(layers.Dense(256, input_shape=(100, ), use_bias=False))
model.add(layers.BatchNormalization())
model.add(layers.LeakReLU())
model.add(layers.Dense(1))
return model
cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)
def discriminator_loss(real_out, fake_out):
real_loss = cross_entropy(tf.ones_like(real_out), real_out)
fake_loss = cross_entropy(tf.zeros_like(fake_out), fake_out)
return real_loss + fake_loss
def generator_loss(fake_out):
return cross_entropy(tf.ones_like(fake_out), fake_out)
generator_opt = tf.keras.optimizers.Adam(1e-4)
discriminator_opt = tf.keras.optimizers.Adam(1e-4)
EPOCHS = 100
noise_dim = 100
num_exp_to_generate = 16
seed = tf.random.normal([num_exp_to_generate , noise_dim])
generator = generator_model()
discriminator = discriminator_model()
def train_step(image):
noise = tf.random.normal([BATCH_SIZE, noise_dim])
with tf.GradientTape() as gen_tape, tf.GradientTape() as disc_tape:
real_out = discriminator(image, training=True)
gen_image = generator(noise, training=True)
fake_out = discriminator(gen_image, training=True)
gen_loss = generator_loss(fake_out)
disc_loss = discriminator_loss(real_out, fake_out)
gradient_gen = gen_tape.gradient(gen_loss, generator.trainable_variables)
gradient_disc = disc_tape.gradient(disc_loss, discriminator.trainable_variables)
generator_opt.apply_gradients(zip(gradient_gen, generator.trainable_variables))
discriminator_opt.apply_gradients(zip(gradient_disc, discriminator.trainable_variables))
def generator_plot_image(gen_model, test_noise):
pre_images = gen_model(test_noise, training=False)
fig = plt.figure(figsize=(4,4))
for i in range(pre_images.shape[0]):
plt.subplot(4, 4, i+1)
plt.imshow((pre_images[i, :, :, 0] + 1)/2, cmap='gray')
plt.axis('off')
plt.show()
def train(dataset, epochs):
for epoch in epochs:
for image_batch in dataset:
train_step(image_batch)
print('.', end='')
generator_plot_image(generator, seed)
train(datasets, EPOCHS)
GAN训练的小技巧
https://github.com/soumith/ganhacks
(1)标准化输入
- 标准化图片,使其在-1~1之间
- Tanh 作为生成器输出的最后一层
(2)修改损失函数
在GAN论文中,生成器G损失函数为 m i n ( l o g ( 1 − D ) ) min(log(1-D)) min(log(1−D)),但实际上使用 m a x ( l o g D ) max(logD) max(logD)
- 因为第一个公式在早期就存在梯度消失的问题
- 训练生成器时翻转标签:real = fake, fake = real
(3)使用球形采样
- 不要从均匀分布中采样
- 从高斯分布中采样
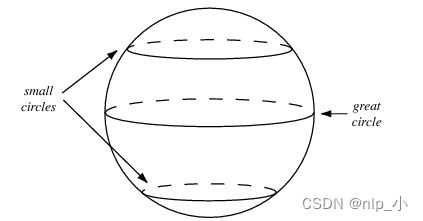
- 进行插值时,通过大圆进行插值,而不是从 A 点到 B 点的直线
- Tom White 的Sampling Generative Networks参考代码https://github.com/dribnet/plat有更多细节
(4)批处理
-
为真假构建不同的小批量,即每个小批量只需要包含所有真实图像或所有生成的图像。
-
当 batchnorm 不是一个选项时,使用实例归一化(对于每个样本,减去均值并除以标准差)。
(5)避免稀疏梯度:ReLU、Maxpool -
如果梯度稀疏,GAN 游戏的稳定性会受到影响
-
LeakyReLU = 好(在 G 和 D 中)
-
对于下采样,使用:Average Pooling,Conv2d + stride
-
对于上采样,使用:PixelShuffle、ConvTranspose2d + stride
- PixelShuffle: https /arxiv.org/abs/1609.05158
(6)使用Soft和Noisy 标签
- Label Smoothing,即如果你有两个目标标签:Real=1 和 Fake=0,那么对于每个传入的样本,如果是真实的,则将标签替换为 0.7 到 1.2 之间的随机数,如果是假样本,将其替换为 0.0 和 0.3(例如)。
- 萨利曼斯等。人。2016 年
- 使标签成为鉴别器的噪声:在训练鉴别器时偶尔翻转标签
(7)DCGAN/混合模型
- 尽可能使用 DCGAN。有用!
- 如果你不能使用 DCGAN 并且没有稳定的模型,请使用混合模型:KL + GAN 或 VAE + GAN
(8)使用强化学习的稳定性技巧
- 体验重播
- 保留过去几代人的回放缓冲区并偶尔显示它们
- 保留 G 和 D 过去的检查点,并偶尔将它们交换出来进行几次迭代
- 所有适用于深度确定性策略梯度的稳定性技巧
- 参见 Pfau & Vinyals (2016)
(9)使用 ADAM 优化器
- optim.Adam 规则!
- 参见 Radford 等。人。2015
- 判别器使用 SGD,生成器使用 ADAM
(10)尽早跟踪失败
- D loss 变为 0:故障模式
- 检查梯度规范:如果超过 100 个,那就搞砸了
- 当一切正常时,D loss 的方差很小,并且随着时间的推移而下降,而不是具有巨大的方差和尖峰
- 如果生成器的损失稳步减少,那么它就是在用垃圾愚弄 D(马丁说)
(11)不要通过统计来平衡损失(除非你有充分的理由)
- 不要试图找到一个(G数/D数)时间表来展开训练
- 这很难,我们都试过了。
- 如果您确实尝试过,请采用有原则的方法,而不是直觉
while lossD > A:
train D
while lossG > B:
train G
(12)如果你有标签,使用它们
- 如果您有可用的标签,则训练鉴别器以对样本进行分类:辅助 GAN
(13)向输入添加噪声,随时间衰减
- 在 D 的输入中添加一些人工噪声(Arjovsky 等人,Huszar,2016)
- http://www.inference.vc/instance-noise-a-trick-for-stabilising-gan-training/
- https://openreview.net/forum?id=Hk4_qw5xe
- 向生成器的每一层添加高斯噪声(Zhao et. al. EBGAN)
- 改进的 GANs:OpenAI 代码也有(注释掉)
(14)[不确定] 训练判别器更多(有时)
- 尤其是当你有噪音时
- 很难找到 D 次迭代与 G 次迭代的时间表
(15)[不确定]批量歧视
- 结果好坏参半
(16)条件 GAN 中的离散变量
- 使用嵌入层
- 添加为图像的附加通道
- 保持嵌入维度低并上采样以匹配图像通道大小
(17)在训练和测试阶段都使用 G 中的 Dropouts
- 以 dropout (50%) 的形式提供噪声。
- 在训练和测试时应用到我们的生成器的几层
- https://arxiv.org/pdf/1611.07004v1.pdf