代码随想录刷题记录day17之寻找树左下角的值+求路径总和+构造二叉树
代码随想录刷题记录day17之寻找树左下角的值+求路径总和+构造二叉树
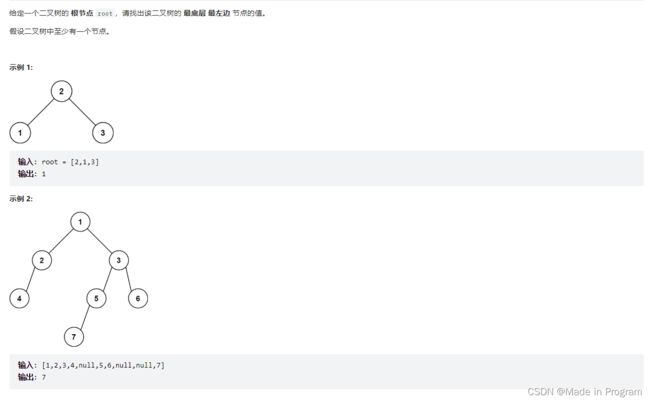
513. 找树左下角的值
思想
用两个变量,maxHeight,res
其中maxHeight维护最大深度,res维护结果
本题不涉及 对中间节点的操作,所以前中后序遍历都可以,只要左在前就i好了。
即使处于同一层,会先遍历左节点,所以res记录的是最左边的值。
代码
class Solution {
private int maxHeight=Integer.MIN_VALUE;//用来记录深度
private int res;
public int findBottomLeftValue(TreeNode root) {
//需要确定是不是最底层的
//前序遍历
leftValue(root,1);
return res;
}
public void leftValue(TreeNode node,int deepth){
if(node.left==null && node.right==null) {
if(deepth>maxHeight){
//因为都是左节点先操作 如果在同一层 这里的代码不会被执行 deepth=maxHeight
maxHeight=deepth;
res=node.val;
}
return;
}
//判断是不是左节点 通过父节点来判断
if(node.left!=null){
deepth++;
leftValue(node.left,deepth);
deepth--;
}
if(node.right!=null){
deepth++;
leftValue(node.right,deepth);
deepth--;
}
}
}
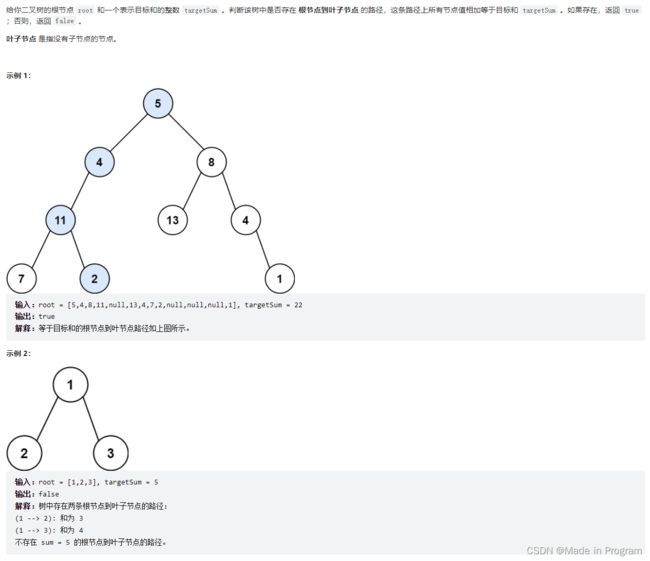
112. 路径总和
思想
需要回溯、且递归函数有返回值
-
递归终止条件是叶节点,将当前的叶节点的值+sum,判断是否和目标值相等 。
-
单层递归逻辑:
当前的值的左节点不为空,判断左方向是否有符合条件的,向上返回
右节点同理
代码
class Solution {
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root==null) return false;
return path(root,targetSum,0);
}
public boolean path(TreeNode node,int targetSum,int sum){
//递归终止条件
if(node.left==null && node.right==null){
sum+=node.val;
//找到了目标值
if(sum==targetSum){
return true;
}else{
return false;
}
}
if(node.left!=null){
sum+=node.val;
if(path(node.left,targetSum,sum)) return true;//判断左方向是否有符合条件的,需要向上去返回
sum-=node.val;
}
if(node.right!=null){
sum+=node.val;
if(path(node.right,targetSum,sum)) return true; //函数有返回值,相当于告诉我们右子树 或者右方向的 是否有符合条件的
sum-=node.val;
}
return false;
}
}
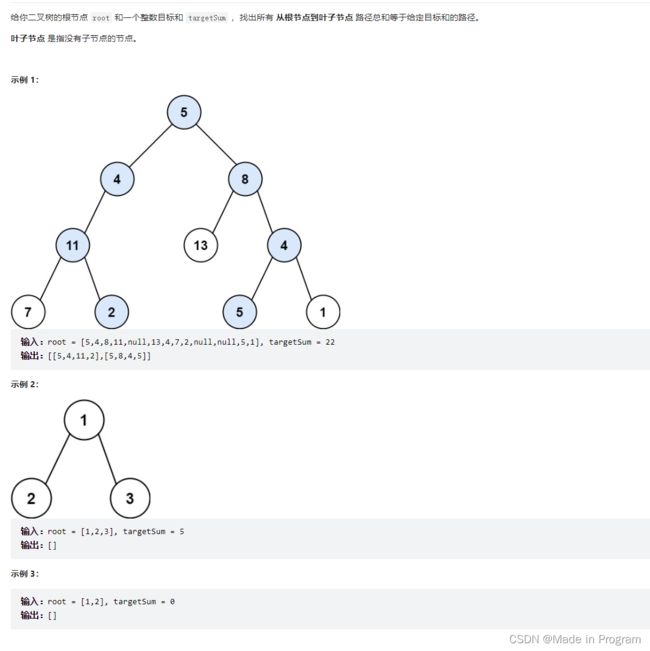
113. 路径总和 II
思想
和上一题思路差不多,只不过多维护了一个集合来记录路径 ,也得回溯
代码
class Solution {
private List<List<Integer>> res=new ArrayList<>();
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<Integer> path=new ArrayList<>();
if(root==null){
return res;
}
traversal(root,targetSum,0,path);
return res;
}
public void traversal(TreeNode node,int targetSum,int sum,List<Integer> path){
//递归终止条件
//System.out.println(sum);
if(node.left==null && node.right==null){
//递归到了叶子节点了 判断是否与目标值相等
sum+=node.val;
path.add(node.val);
if(sum==targetSum){
res.add(new ArrayList<>(path));//结果中添加一个数组
}
sum-=node.val;
path.remove(path.size()-1);
return;
}
//单层内的递归逻辑
if(node.left!=null){
sum+=node.val;
path.add(node.val);
traversal(node.left,targetSum,sum,path);
path.remove(path.size()-1);
sum-=node.val;
}
if(node.right!=null){
sum+=node.val;
path.add(node.val);
traversal(node.right,targetSum,sum,path);
path.remove(path.size()-1);
sum-=node.val;
}
}
}
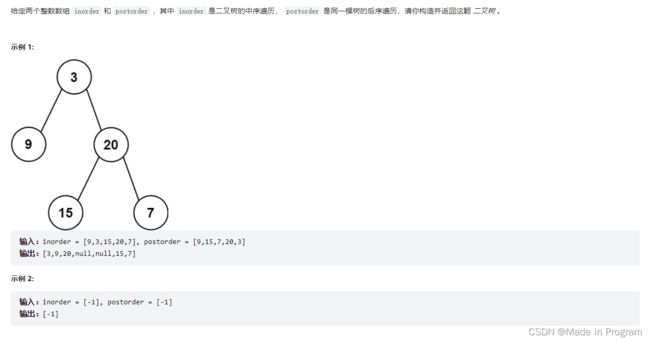
106. 从中序与后序遍历序列构造二叉树
思想:
1.后序遍历的最后一个元素确定根节点的位置
2.根据根节点去中序中切分中序数组,为左中序数组和右中序数组
3.根据左中序数组和右中序数组 的大小,再去切分后序遍历的数组,得到左后序数组和右后序数组
3.递归调用
需要注意下标的区间问题,打印日志调试。
犯了一个错误,以为得到左中序数组和右中序数组了,左后序数组和右后序数组的顺序会与之相同,结果显然不是。
代码
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return tree(inorder,postorder);
}
public TreeNode tree(int[] inorder, int[] postorder){
//递归终止条件:后序中的长度为0
if(postorder.length==0){
return null;
}
int rootValue=postorder[postorder.length-1];//后序遍历中的最后一个元素就是根节点
//System.out.println("根节点值:"+rootValue);
TreeNode root=new TreeNode(rootValue);
int index=0;
for(int i=0;i<inorder.length;i++){
//根据根节点去切割中序遍历 左闭右开
if(inorder[i]==rootValue){
index=i;
break;
}
}
//System.out.println("根节点下标:"+index);
//构造左中序列
int[] leftIn=Arrays.copyOfRange(inorder,0,index);
//System.out.println("左中序"+Arrays.toString(leftIn));
int[] rightIn=Arrays.copyOfRange(inorder,index+1,inorder.length);//右中序列
//System.out.println("右中序"+Arrays.toString(rightIn));
//根据左中序数组 去构建左后序数组
int[] leftPost=new int[leftIn.length];
int[] rightPost=new int[rightIn.length];
for(int i=0;i<leftIn.length;i++){
leftPost[i]=postorder[i];
}
//System.out.println("左后序"+Arrays.toString(leftPost));
for(int i=0;i<rightIn.length;i++){
rightPost[i]=postorder[index+i];
}
// System.out.println("右后序"+Arrays.toString(rightPost));
root.left=tree(leftIn,leftPost);
root.right=tree(rightIn,rightPost);
return root;
}
}
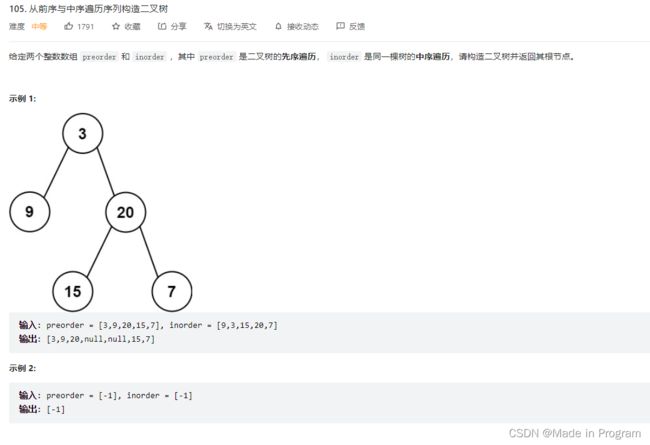
105. 从前序与中序遍历序列构造二叉树
思想
和106题类似
代码
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return tree(preorder,inorder);
}
public TreeNode tree(int[] preorder,int[] inorder){
if(preorder.length==0) return null;
int rootValue=preorder[0];//前序遍历的第一个元素就是根节点
TreeNode root=new TreeNode(rootValue);
//根据根节点去中序中切分
int index=0;
for(int i=0;i<inorder.length;i++){
if(inorder[i]==root.val){
index=i;
break;
//找到了 下标 即第一轮 3的位置 下标为1
}
}
//根据下标去切分左中序 和右中序
int [] leftIn=Arrays.copyOfRange(inorder,0,index);
//System.out.println("左中序"+Arrays.toString(leftIn));
int [] rightIn=Arrays.copyOfRange(inorder,index+1,inorder.length);
//System.out.println("右中序"+Arrays.toString(rightIn));
//根据左中序 和右中序 去切分前序数组
int [] leftPre=new int[leftIn.length];
int [] rightPre=new int[rightIn.length];
for(int i=0;i<leftIn.length;i++){
leftPre[i]=preorder[i+1];
}
//System.out.println("左前序"+Arrays.toString(leftPre));
for(int i=0;i<rightIn.length;i++){
rightPre[i]=preorder[leftIn.length+1+i];
}
//System.out.println("右前序"+Arrays.toString(rightPre));
root.left=tree(leftPre,leftIn);
root.right=tree(rightPre,rightIn);
return root;
}
}